流变应力恢复法地应力测试及装置

张 芳，刘泉声,，张程远,，蒋景东

（1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；2.武汉大学 土木建筑工程学院，武汉 430072）

1 引 言

地应力是引起地下工程岩体变形和破坏的根本作用力，精确获取地应力矢量值是确定工程岩体力学属性，进行围岩稳定性分析，实现地下工程开挖支护设计和决策科学化的必要前提[1]。关于地应力测量的研究工作已近百余年，提出的地应力测试方法与理论有很多[1－5]，如水压致裂法、应力解除法、声发射法、扁千斤顶法、BWSRM法等。然而由于精度、适用范围等局限性以及工程岩体特殊性等问题，目前工程实践中最常用的地应力测试方法主要是水压致裂法和应力解除法[7－12]。随着浅部煤炭资源的日益减少和枯竭，中东部国有重点煤矿均已进入深部开采阶段[13]。煤矿深部围岩软弱、破碎，现常用的地应力测试方法难以成功应用。

如水压致裂法，其钻孔封隔器需要在高水压下具备良好的水密封性能，因而该方法对岩体的完整性提出了苛刻的要求，因此水压致裂法更适宜用于完整硬岩体的应力测试。而且该方法只能确定垂直于钻孔平面内的最大主应力和最小主应力，钻孔方向假设为一个主应力方向，其本质上为二维应力测量方法。因此，水压致裂法假定较多，局限性较强。对于应力解除法，为了计算应力值，首先必须确定岩体的物理力学性质参数以及所测物理量和应力的相互关系（本构关系）。对含裂隙软岩体而言，其物性参数的取值与岩体所受应力状态和岩体试件大小及形状密切相关，不同应力状态下不同大小的岩体试件通过试验得出物性参数数值可相差数倍甚至十倍以上，这就要求采用应力解除法测试地应力时必须取得超过传感器长度（一般不短于30 cm）的完整岩芯，且在模拟应力解除过程中的应力状态（即厚壁圆筒外壁均匀受压的应力状态）下获取岩芯的物性参数等。很显然，这些要求过于苛刻，例如，煤矿深部松软岩体多为泥质胶结，经受了高应力的作用，取芯过程中受水流冲刷和应力强卸荷作用，多数情况下连长度为10 cm的短岩芯也难以获取，因而很难通过单轴压缩试验得到准确的岩体物理力学参数。因此，应力解除法假定较多，实施困难，局限性也较强。而其他的岩体应力测试方法，如声发射法等，也很难胜任软岩体应力测试。这就要求提出一种新的适用于软岩体应力测试的方法及装置。

中国专利[14－19]公开了几种压应力传感器，经综合比较后发现主要存在以下问题：①工程实践中现用压应力传感器大多只能测一维压力，不能同时测得3个方向上的压力。②工程实践中现用压应力传感器大多是基于电信号或电相关信号的，没有取得防爆证，不能在富含瓦斯的煤矿井下等恶劣环境中使用。③专利中提到了几种三向压应力传感器，但是没有成品，尚未在工程实践中应用，而且其公布的测试原理及装置尚不完善。因此，针对工程实践的迫切要求，作者研制了一种可以同时测得三方向正应力的压应力传感器，并提出了与之相适应的测试方法，同时对压应力传感器进行了标定和室内模型试验。

与传统测量方法相比，本文提出的地应力测试方法及装置主要有以下优点：①适用于软岩体；②能同时测得三方向正应力，并经解算可得一点空间应力状态；③能实时监测一点应力状态的演化过程；④本质安全，可用于煤矿等领域；⑤能实现准分布式测量，得到某一区域的应力场；⑥测量精度相对较高。

2 测试方法

在煤矿深部高地应力作用下，直径较小的钻孔周围岩体处于破碎状态，具有一定的流变性（高应力状态下的挤压变形），即使不充填，钻孔也会发生明显收缩，直至完全封闭，封闭后孔周岩体随时间延长而逐渐挤密，赋存应力随之增高，如图1所示。如果孔内主动充填，限制钻孔收缩变形，孔周岩体应力会恢复得更高。因此，在钻孔中置入随深度和方向而变化的一系列传感器，并注浆固定。孔周岩体为松软破碎围岩，在高地应力作用下，具有流变性，随时间推移，钻孔中各点应力会逐渐增加，最后趋于稳定。

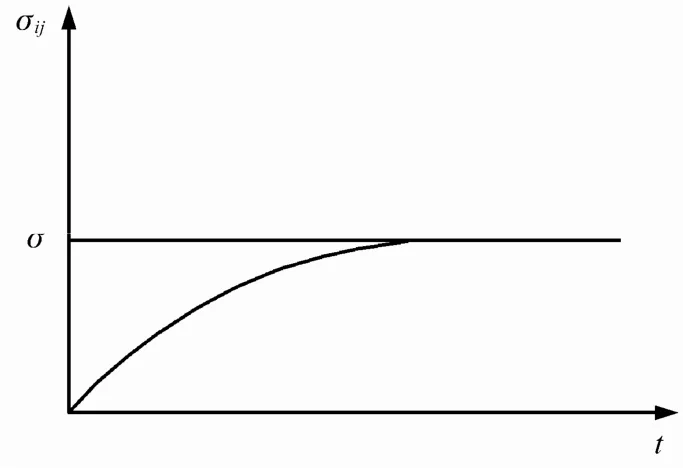
图1 恢复应力随时间变化关系Fig.1 Changes of restress with time

流变应力恢复法地应力测试方法可一次同时测得一点空间应力状态 σx、σy、σz、τyz、τzx、τxy。其测试原理是这样的：一个三向压应力传感器可以测得3个正应力分量 σx、σy、σz，那么两个互成一定角度（该角度原则上是任意的，但前提是使应力分量转轴公式有解）的三向压应力传感器可以测得 6个正应力分量 σx、σy、σz、σx′、σ ′y、σz′ 。以其中一个三向压应力传感器盒体某一顶点为原点o，相互垂直的3条棱边为3个坐标轴方向x、y、z，建立空间坐标系oxyz；以另一个压应力传感器盒体的对应顶点为原点o′，相互垂直的3条棱边为3个坐标轴方向x′、y′、z′，建立空间坐标系o′ x′ y ′z′（o和o′相距较近，可近似认为重合），如图2所示。

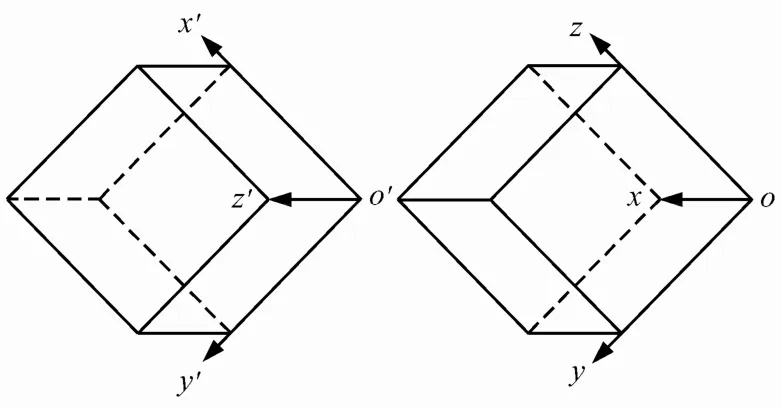
图2 传感单元组合方式Fig.2 Combination of sensing unit

当坐标轴作转轴变换时，应力分量遵循张量变换规律。坐标轴旋转后，应力状态的6个应力分量均有改变，但是作为一个整体所描述的应力状态是不会发生变化的。

设l1、l2、l3分别为x′、y ′、z ′ 轴与x轴之间的方向余弦；m1、m2、m3分别为x′、y ′、z ′ 轴与y轴之间的方向余弦；n1、n2、n3分别为x′、y ′、z ′ 轴与z轴之间的方向余弦。将 6个正应力分量σx、σy、σz、σx′、σ ′y、σz′及各个方向余弦l1、l2、l3、m1、m2、m3、n1、n2、n3代入下列应力分量转轴公式[20]，即可解算出所测点处的空间应力状态。

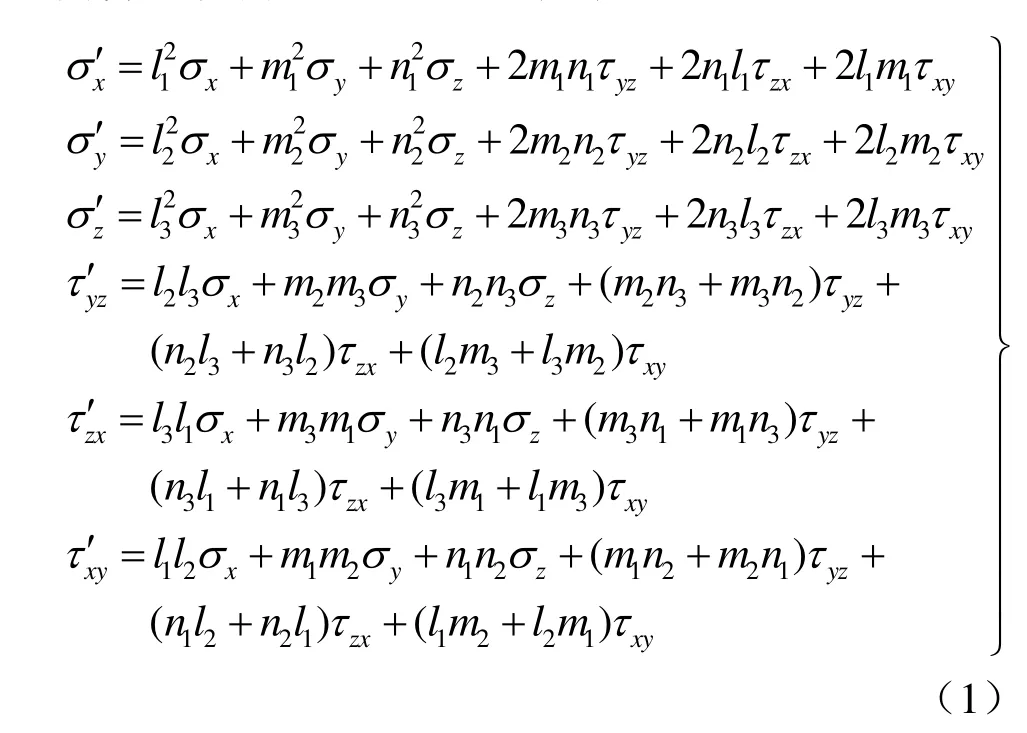
式中：σx、σy、σz为测试单元内第1个传感器所测3个正应力分量；τyz、τzx、τxy为第1个传感器所测3个剪应力分量；σx′、σ ′y、σz′ 为测试单元内第2个传感器所测3个正应力分量；τ′yz、τz′x、τx′y为第2个传感器所测3个剪应力分量。应力张量为二阶对称张量，仅有6个独立分量。新坐标系下6个应力分量可通过原坐标系下应力分量确定，因此，应力张量的6个应力分量就确定了一点的应力状态（该方法已申请专利，专利申请号为：201210096644.6）。

3 测试装置

作者研制了一种基于振弦式传感的岩土三向压应力传感器，其示意图如图3所示。

图3 压应力传感器示意图Fig.3 Schematic of pressure stress sensor

压应力传感器从整体上来说为立方体式结构，8个棱角被削去，其中共顶点的3个面为传感面，其上连接有弹性承载板，另外3个面则为受力面。当承载板受法向力p作用时，即产生弯曲变形，固定在承压板上的立柱（如图4中的A、B）随之发生转动。显然，紧绷于两根立柱间的钢弦所受张力T也相应的产生变化（理论分析认为，对于同一压力盒，在弹性变形阶段，T与p之间的关系是惟一的），此钢弦即为振弦式压应力传感器的敏感元件。为了测定该钢弦张力T的变化，需要在钢弦下方设置激振线圈，若给线圈施加一个脉冲电压信号，线圈所产生的磁场将使钢弦作正弦式振动，从而使得自振钢弦与激振线圈之间产生周期性的变化，线圈回路中的磁阻抗也相应的产生周期性变化，由线圈感应出的磁阻变化频率为钢弦的自振频率。因此，可通过钢弦张力的变化情况建立被测介质的压力p与钢弦自振频率f两者之间的关系。

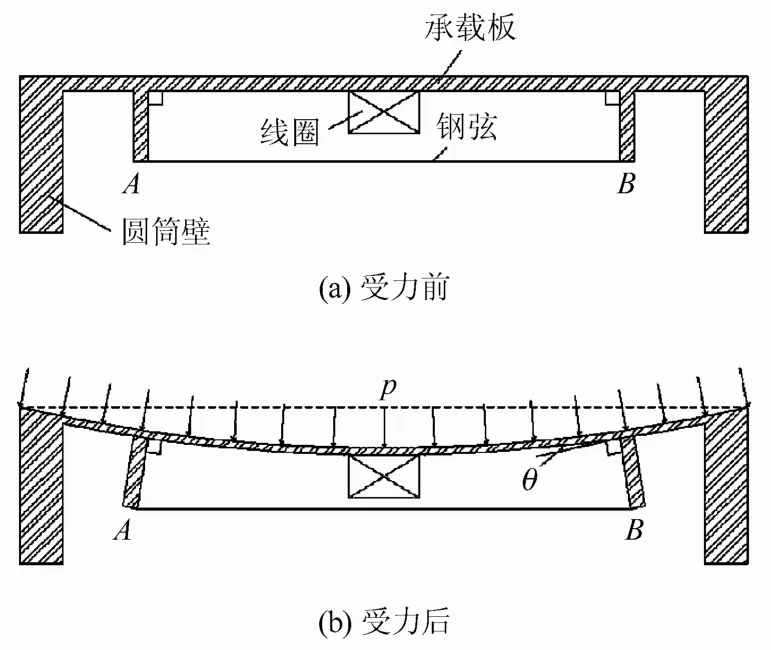
图4 振弦式传感器测压原理Fig.4 Measuring principle of vibrating wire sensor

设振弦式压应力传感器的敏感元件钢弦是一根做微小振动的理想的钢弦，在弦上取其中一段MN，设MN的两端受拉力为T和T′，弦的线密度为ρ。根据钢弦在时刻t的受力情况，可由牛顿第二定律，列出满足于动位移y(x,t)地弦振动方程[21]为

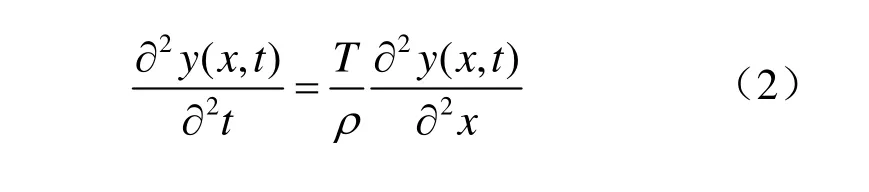
两端固定弦的边界条件为 y(0,t)= y(l,t) = 0，初始条件为 v(x,0)=λδ(x−l/2)，λ为δ的脉冲宽度，λ=π/l。

采用分离变量法求解式（2）得

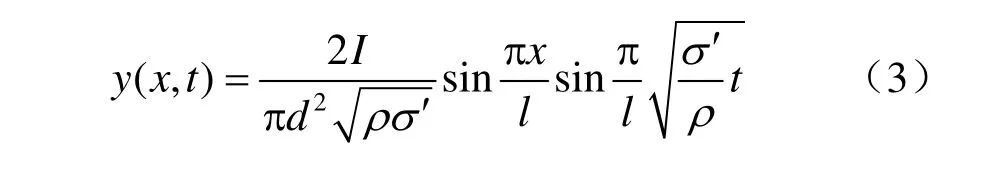
式中：I为激振冲量；l为钢弦的长度；d为钢弦的直径；σ′为钢弦应力。

显然，式（3）为正弦函数，其频率f为

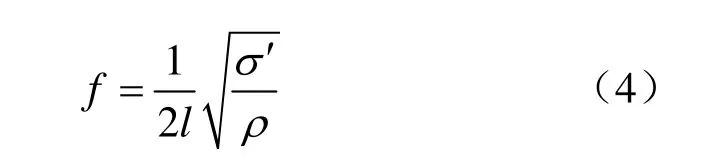
将式（4）改写为

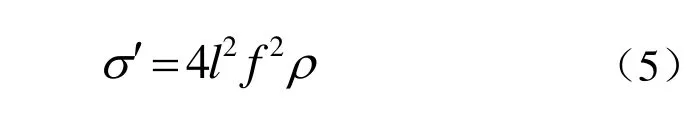
当承载板在法向压力p作用下，设弦所受到应力的增量为Δσ，由于压力盒的钢弦初始应力σ′是固定的，可以简称钢弦的应力增量Δσ，即为钢弦应力σ。

故有

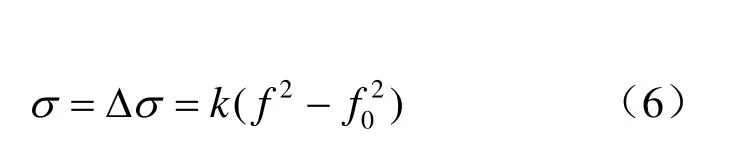
式中：k为钢弦的灵敏系数，k =4l2ρ；f为压力盒在外力作用下的钢弦频率；f0为钢弦的初始频率。

根据虎克定律，有

钢弦的应变可由式（7）确定，从图4可以得出，由于立柱和承载板的相对位置保持不变，即承载板与立柱始终保持相互垂直，因此承载板受力后在立柱所在的位置切线的转角与立柱转角相等，设为θ。显然，由几何分析可以建立钢弦长度l和应变ε与θ之间的关系，然后由静力分析可建立承载板所受压力p与θ的相互关系。

由弹性力学中圆形薄板轴对称弯曲理论可计算出：

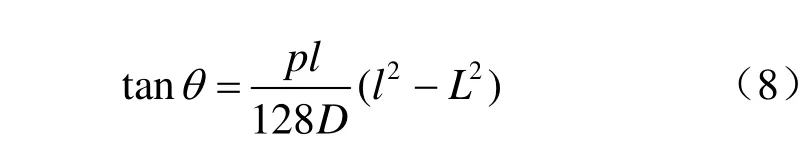
式中：p为作用于承载板上法向的均布荷载（MPa）；L为承载板的直径（mm）；D为承载板弯曲刚度，D= Eb3/12(1−μ2)；E为承载板的弹性模量（MPa）；μ为承载板的泊松比；b为承载板的厚度（mm）。

由式（7）可得

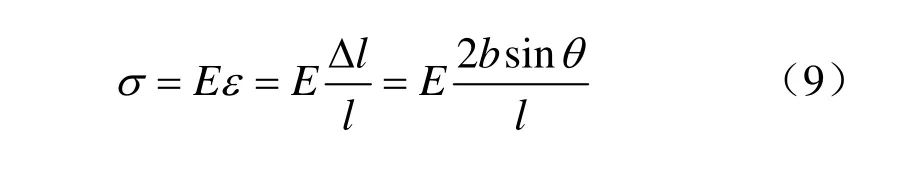
式中：b为立柱高度（mm）。

由于为微小的变形，tanθ=sinθ，故有

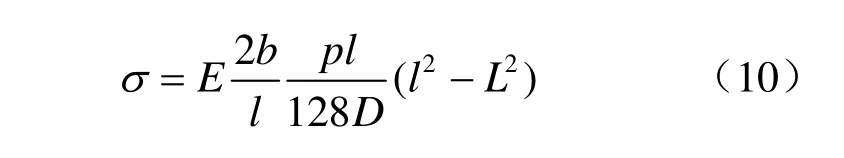
由式（6）与式（10），考虑到弹性力学中对应力正负号规定，可以得出：

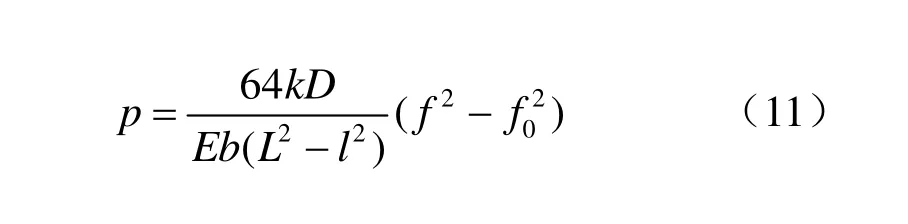
将式（11）改写成

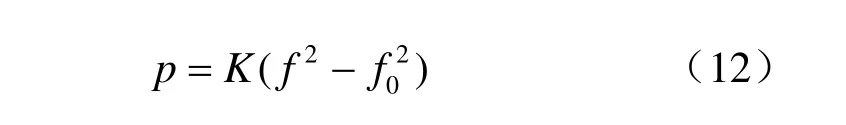
4 标定试验

为验证压应力传感器是否能正常工作，并得到传感器参数K值等，进行了标定试验。在标定之前先对传感器各个传感面进行了3次预加载，每次预加载都达到标准荷载60 kN（传感面对应的应力约为25 MPa，即传感器最大量程约为25 MPa）。压应力传感器的量程与承载板有关，承载板越厚，尺寸（直径）越小，压应力传感器量程则越大；反之，则越小。而压应力传感器的量程与精度是呈反相关关系的，因此需在量程与精度之间找出一个最优点，使得精度较高满足工程实践要求，同时量程较大应用范围较广。

其主要目的是：①使试验相关组件各部分接触良好，更好地进入正常工作状态，且若干次预加载之后使荷载与读数之间的关系趋于稳定；②检查整个试验装置是否安全可靠；③检查传感器以及测试仪器仪表等能否正常工作；④使试验人员更好地熟悉相关操作，从而保证标定试验顺利进行。

标定试验是在中国科学院武汉岩土力学研究所自行研制的RMT150C岩石力学试验系统上进行的，试验机架刚度为 5000 kN/mm。试验采用力-位移控制方式，力传感器最大量程为100 kN，加载速率为0.2 kN/S，力传感器与压应力传感器之间有一根钢柱作为传力柱，以弥补试验机冲程过短的不足，如图5所示。

图5 标定实验示意图Fig.5 Schematic of calibration test

本文以压应力传感器的1面为例进行标定，每6 kN为一级，一共10级，进程和回程都记录下每级荷载所对应的频率值，然后运用式（12）即可解算出相应荷载等级下的系数K值，列于表1中。

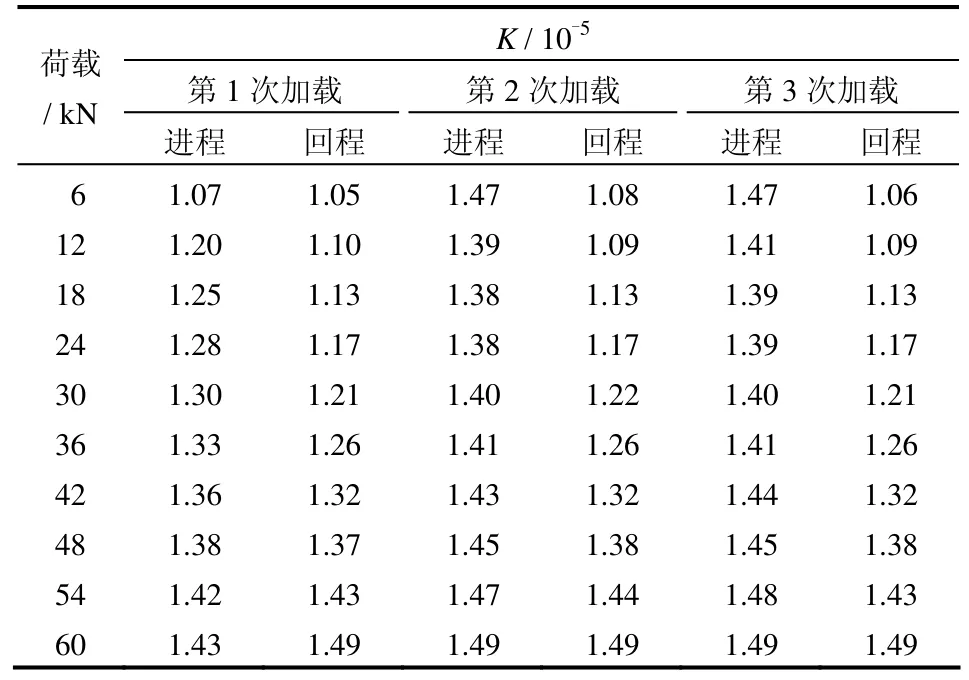
表1 标定试验结果Table1 Calibration test data

由表可见，K值从整体上来说是稳定的，即传感器的线性度和重复性均较好，这与前面理论推导中认为K值只与压应力传感器尺寸和材质有关是一致的，因此根据表 1可计算出 K值的平均值为1.32×10-5。得到K值后，再根据式（12）反算荷载值列于表2中。

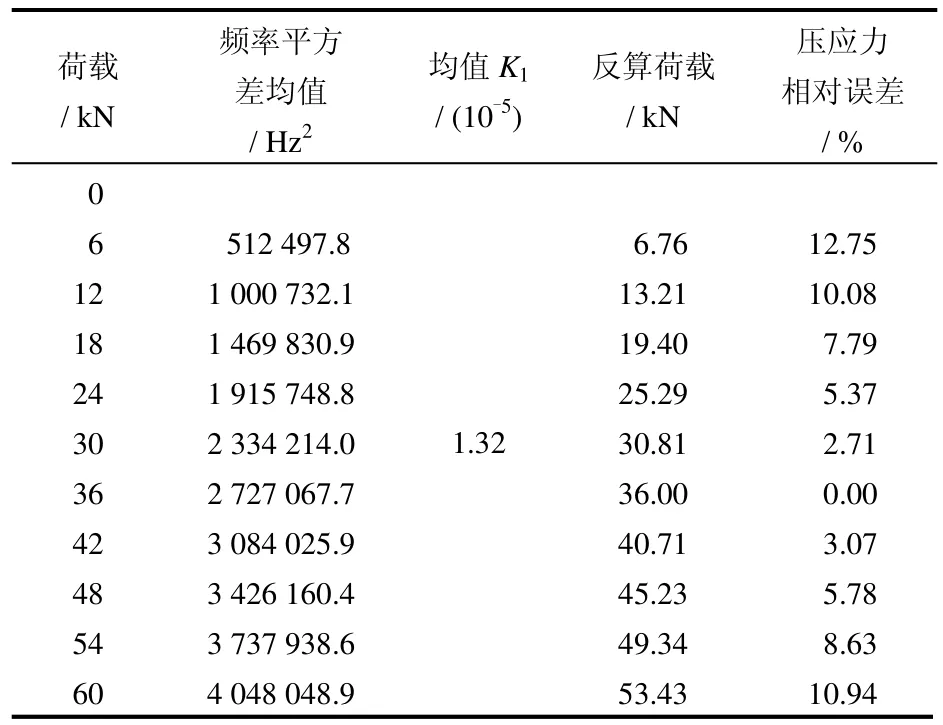
表2 标定结果验算Table 2 Calibration results checking

可以发现：当荷载偏小或偏大时，压应力传感器测量误差较大，一度高达10%左右，而当荷载适中时，相对误差较小，甚至可忽略不计。分析认为主要原因是：①制作压应力传感器的钢材质量不好，热处理性能不好，钢材内部有残余应力/应变等，对标定结果有一定影响；②传力柱刚度不够，当受力时内部存储有应变能，对标定结果有一定的影响；③试验机上的力传感器最大量程达到100 kN，而对压应力传感器所施加的最大荷载为60 kN，力传感器量程偏大导致精度不够，可能对标定结果带来一定影响。但总的来说，从0～60 kN，K值平均值为1.32×10-5，以此反算荷载的平均相对误差为6.71%，基本满足工程实践要求。

为了解传感器3个传感面之间是否存在相互干扰，补充进行了3组干扰（标定）试验，试验结果如图6所示。

如图6(a)～(c)所示，当σ2、σ3分别等于5、10、15 MPa（即围压分别为5、10、15 MPa）时，传感面1反复加载3次的结果曲线线性度、重复性均较好，说明围压大小基本上不影响面1的传感性能。如图6(d)所示，当 σ2=5 MPa,σ3= 10 MPa时，面1反复加载3次的结果曲线线性度、重复性均较好，即面2和面3不等受力不影响面1的传感性能。

综上可说明，传感器3个传感面之间的相互干扰可以忽略不计。

5 模型试验

对压应力传感器进行标定之后，为进一步验证其传感性能，并探讨在软岩体工程中实用可行性，进行了模型试验。模型试验是在课题组自行研制的真三轴模型装置上进行的，如图7所示。

模型试验的基本思路：以强度较低的水泥砂浆块体（如M2.5）模拟软岩体，将压应力传感器浇筑于水泥砂浆块体中心处，保证压应力传感器的6个面分别与水泥砂浆块体的6个面平行，然后把水泥砂浆块体置于真三轴模型装置上，进行有侧限单轴压缩试验，同时观测压应力传感器所测应力值与理论计算应力值是否一致，以探讨压应力传感器在岩体工程中使用的可行性。

水泥砂浆块体设计抗压强度为5 MPa，尺寸为0.6 m×0.6 m×0.6 m，以压应力传感器的1面为例进行单轴压缩试验，试验结果如表3和图8所示。

根据试验结果可以发现：

（1）当所施加压力较小时，压应力传感器所感知的力很小。这可能是因为：①水泥砂浆块体本身有一定的孔隙度，当其受力时会逐渐被压密，而在被压密的这个过程中，传递到传感面上的力很小。②由于传感器的传感原理是基于传感面产生弹性变形的，而水泥砂浆块体本身有一定的刚度，水泥砂浆块体与传感面两种材料之间的变形并不一定是完全匹配的。

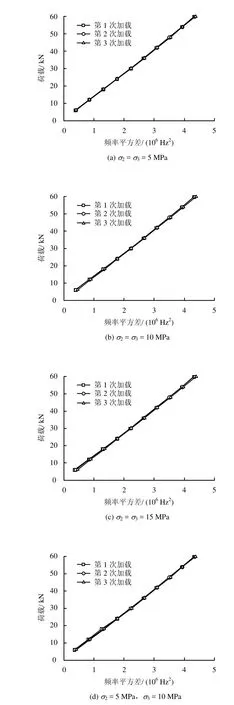
图6 干扰试验结果Fig.6 Results of interference tests

图7 真三轴模型装置Fig.7 True triaxial apparatus

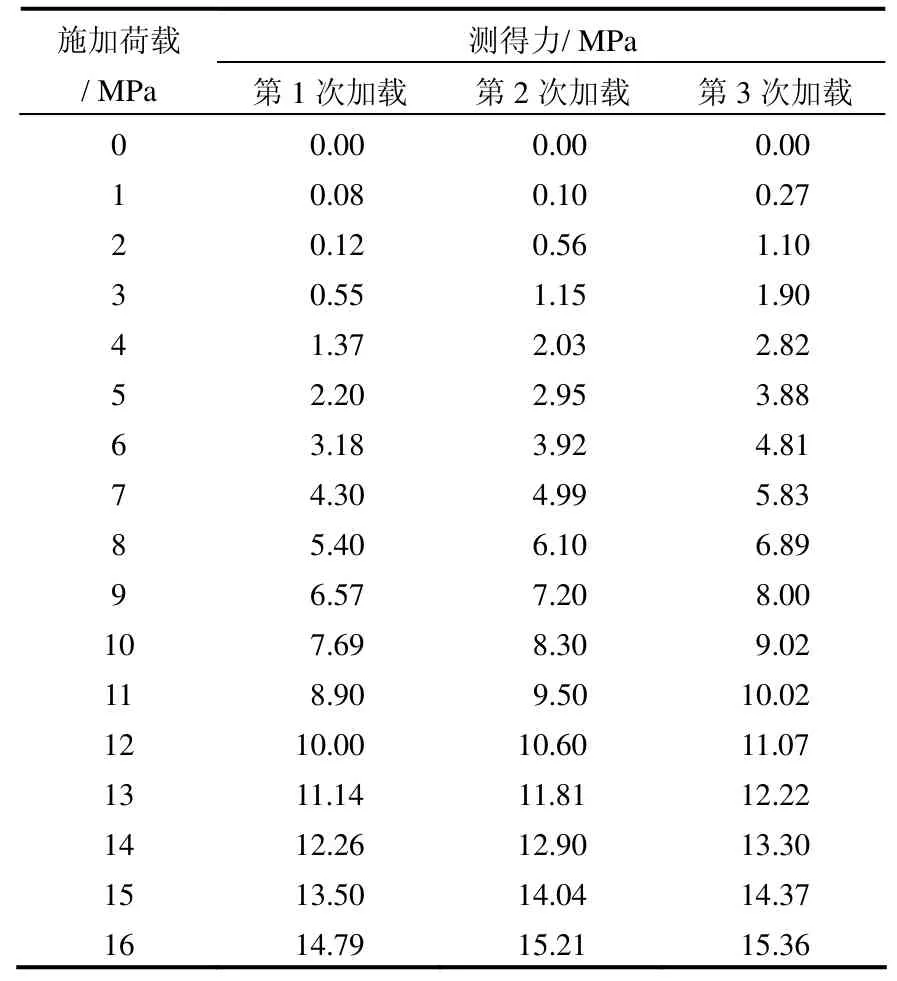
表3 模型试验结果Table 3 Model test results

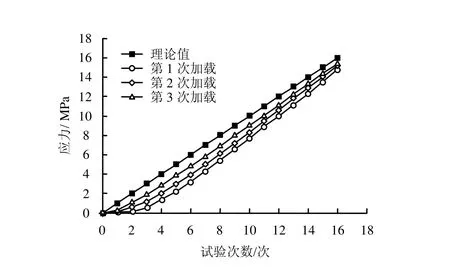
图8 模型试验结果曲线Fig.8 Curves of model test results

（2）当施加压力越来越大时，压应力传感器所感知的力越来越接近于理论值。这可能是因为当水泥砂浆块体被压密之后，所施加的压力更易传递到传感面上。

（3）随着加载次数的增加，传感器所测应力值会越来越接近于理论计算值。这可能是因为每一次加载都会压密水泥砂浆块体；而且第1次加载之后，水泥砂浆块体很可能已被压坏，呈破碎状态。

6 结 论

煤矿深部围岩软弱破碎，常规地应力测试方法（如水压致裂法、应力解除法、声发射法等）难以见效。因此，本文提出了1种流变应力恢复法地应力测试方法，并研制了相应的测试装置，且重点对测试装置进行了初步试验分析，具体可归纳为以下几点：

（1）流变应力恢复法地应力测试方法利用两个三向压应力传感器组成一个测试单元，可以测得一点的空间应力状态，且不需要对岩体等作任何假设，原理简单。

（2）岩土三向压应力传感器在标定试验和模型试验中的误差都在10%以内，基本满足工程实践要求。

（3）模型试验中，加载次数越多，加载压力越大，压应力传感器所测应力值越接近理论计算值。

（4）有必要继续优化压应力传感器，提高其测试精度，同时增加其量程，研究三方向传感性能等，并应用于软岩体工程实践，以工程实践应力测试数据更好地指导优化思路。

[1]蔡美峰,乔兰,李华斌.地应力测量原理和技术[M].北京: 科学出版社,2000.

[2]HAIMSON,BEZALEL,FAIRHURST,et al.Initiation and extension of hydraulic fractures in rocks[J].Society of Petroleum Engineers,1967,7(3): 310－318.

[3]AMADEI B,STEPHANSSON O.Rock stress and its measurement[M].London: Chapman and Hall,1997

[4]BOYCE G M.A study of the acoustic emission response of various rock types[D].Philadelphia: Drexel University,1981.

[5]赵奎,闫道全,钟春晖,等.声发射测量地应力综合分析方法与实验验证[J].岩土工程学报,2012,34(8):1403－1410.ZHAO Kui,YAN Dao-quan,ZHONG Chun-hui,et al.Comprehension analysis method and experimental verification for in-situ stress measurement by acoustic emission tests[J].Chinese Journal of Geotechnical Engineering,2012,34(8): 1403－1410.

[6]葛修润,侯明勋.三维地应力 BWSRM 测量新方法及其测井机器人在重大工程中的应用[J].岩石力学与工程学报,2011,30(11): 2161－2178.GE Xiu-run,HOU Ming-xun.A new 3D in-situ rock stress measuring method: Borehole wall stress relief method(BWSRM) and development of geostress measuring instrument based on BWSRM and its primary applications to engineering[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(11): 2161－2178.

[7]康红普,林建,张晓,等.潞安矿区井下地应力测量及分布规律研究[J].岩土力学,2010,31(3): 827－830.KANG Hong-pu,LIN Jian,ZHANG Xiao,et al.In-situ stress measurements and distribution laws in Lu’an underground coal mines[J].Rock and Soil Mechanics,2010,31(3): 827－830.

[8]安其美,丁立丰,王海忠.福建周宁水电站水压致裂地应力测量及其应用[J].岩土力学,2004,25(10): 1672－1675.AN Qi-mei,DING Li-feng,WANG Hai-zhong.Research of crust stress measurement and its application with hydraulic fracturing in Zhouning Hydropower,station of Fujian province[J].Rock and Soil Mechanics,2004,25(10): 1672－1675.

[9]蔡美峰,陈长臻,彭华,等.万福煤矿深部水压致裂地应力测量[J].岩石力学与工程学报,2006,25(5): 1069－1073.CAI Mei-feng,CHEN Chang-zhen,PENG Hua,et al.In-situ stress measurement by hydraulic fracturing technique in deep position of Wanfu coal mine[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(5): 1069－1073.

[10]刘泉声,刘凯德.淮南矿区深部地应力场特征研究[J].岩土力学,2012,33(7): 2089－2095.LIU Quan-sheng,LIU Kai-de.Characteristics of in-situ stress field for deep levels in Huainan coal mine[J].Rock and Soil Mechanics,2012,33(7): 2089－2095.

[11]汪波,何川,吴德兴,等.苍岭特长公路隧道地应力场反演分析[J].岩土力学,2012,33(2): 629－634.WANG Bo,HE Chuan,WU De-xing,et al.Inverse analysis of in-situ stress field of Cangling super-long highway tunnel[J].Rock and Soil Mechanics,2012,33(2): 629－634.

[12]蔡美峰,何满朝,刘东燕.岩石力学与工程[M].北京:科学出版社,2002.

[13]何满潮,谢和平,彭苏萍,等.深部开采岩体力学研究[J].岩石力学与工程学报,2005,24(16): 2803－2811.HE Man-chao,XIE He-ping,PENG Su-ping,et al.Study on rock mechanics in deep mining engineering[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(16): 2803－2811.

[14]周国玉,王千山.电阻应变压轴式土压力盒[P].中国专利: 03212896.7,2004-08-25.

[15]安徽理工大学.一种冲气式双模防水压力盒[P].中国专利: 201120082368.9,2011-10-05.

[16]中国科学院武汉岩土力学研究所.土压力盒埋设装置及其埋设方法[P].中国专利: 200810246303.6,2009-07-22.

[17]宁波杉工结构监测与控制工程中心有限公司.一种光纤布拉格光栅压力传感器及其相应的测量方法[P].中国专利: 201110032714.7,2011-07-06.

[18]河南理工大学.一种岩石三维应力状态的光纤光栅测试装置及测试方法[P].中国专利: 201110052556.1,2011-09-07.

[19]北京科技大学.一种测量三向压力的光纤布拉格光栅传感器[P].中国专利: 200920247115.5,2010-07-21.

[20]徐芝纶.弹性力学[M].北京: 高等教育出版社,1990.

[21]蔡启富.数学物理方程[M].武汉: 武汉水利电力大学出版社,2000.