基于EMD和峭度的Hilbert包络解调在滚动轴承故障诊断中的应用分析*

周 浩，贾民平

(东南大学机械工程学院，江苏南京211189)

0 引 言

据统计，旋转机械的故障有30%是由滚动轴承故障引起的，它的好坏对机器的工作状况影响极大。当滚动轴承局部存在损伤或缺陷时，其振动信号多表现为非平稳、非线性、调制等特征［1］。利用传统单一的时域参数分析法或者频域分析法等方法很难从该类振动信号中提取故障特征信息。

EMD是将信号分解为有限个高频到低频的IMF的和，具有很多独特优点:基函数的自动产生;自适应的滤波特性;自适应的多分辨率;正交性和完备性;IMF分量的调制特性等。上述优点使得EMD已经被应用到许多领域，它非常适合对非线性、非平稳信号进行分析［2］。峭度系数是一个重要的数值统计量，它可以用来描述信号图形顶峰的凸平度。当峭度为3时，分布曲线具有正常峰度(即零峭度);当峭度大于3时，分布曲线具有正峭度，表示信号中冲击成分较多。同时，Hilbert包络解调通过对故障轴承的振动信号进行幅值和频率解调，放大和分离了故障特征信息，极大地提高了信噪比［3］。

基于此，本研究提出一种基于EMD和峭度指标的Hilbert包络解调分析的信号处理方法，通过对仿真信号和实际信号分析，表明该方法可以应用于滚动轴承的故障诊断。

1 EMD方法和Hilbert包络解调

1.1 EMD基本理论

经验模态分解法从本质上来讲就是通过对非平稳信号的分解，来获得一系列表征信号特征时间尺度本征模函数的一种信号平稳化处理方法［4-5］。其中，每个IMF分量必须满足如下2个条件:

(1)本征模函数在整个时间范围内，局部极值点和过零点的个数必须相等，或最多相差1个;

(2)在时间范围内的任意时刻，由局部极大值点形成的上包络线和由局部极小值点形成的下包络线的平均值为零，即上、下包络线关于时间轴呈局部对称。

EMD方法的分解过程如下:

(1)找出原始信号x(t)所有的极大值点和极小值点，并用三次样条插值函数分别拟合这些数据点，形成上、下包络线。

(2)计算上包络线和下包络线的均值m1，将原始信号减去该平均包络得到一个新的数据序列h1:

如果h1全部满足本征模函数的两个条件，则h1就是原始信号x(t)分解出来的第一个IMF分量c1。否则说明h1还不是一个本征模函数，还需将h1作为一个原始信号重复步骤(1)，继续进行筛选，直至产生第一个IMF分量c1。

(3)计算:

再将r1作为原始信号重复步骤(1)～(3)，以该类推得原始信号x(t)的n个满足条件的分量和一个不能再分解的单调函数，即残余分量rn为止［6］，可得:

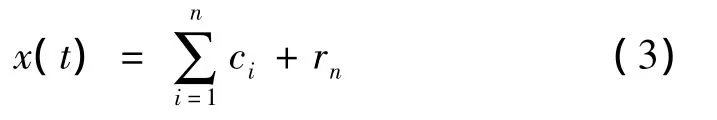
式中:rn—信号的平均趋势。

1.2 Hilbert包络解调

利用希尔伯特变换进行信号包络的原理是让测试信号产生一个90°的相移，从而与原信号构成一个解析信号，该解析信号即构成包络信号［7］。

一个实信号x(t)的希尔伯特变换定义为:

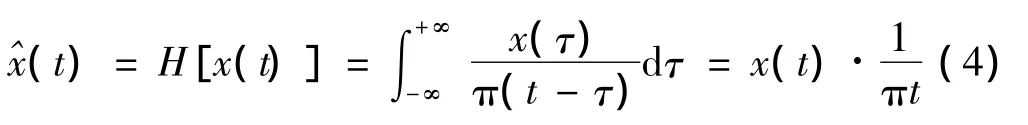
希尔伯特变换的包络A(t)定义为:

瞬时相位φ(t)定义为:

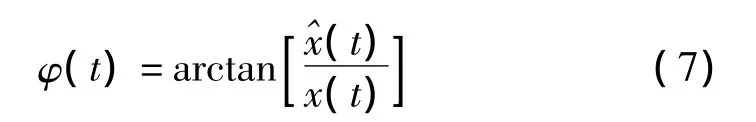
经过希尔伯特变换检波，除去高频的振动分量，然后用含有缺陷激振分量的A(t)代替原始信号x(t)进行频谱分析，便可以进行缺陷的故障诊断［8］。

2 诊断方法

2.1 峭度指标

四阶中心矩也是一个重要的统计估计量。它可以用来表示样本的函数图形顶峰的凸平度，即峭度系数，其数学描述为:

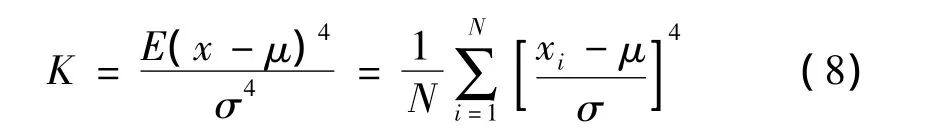
式中:K—原始信号x的峭度指标;N—信号的长度;μ—信号x的均值;σ—信号x的标准差。

当峭度值为3时，分布曲线具有正常峰度(即零峭度)。当标准差小于正常状态下的标准差，即观测值的分散程度较小冲击成分较多时，峭度值增大，此时曲线峰顶的高度高于正常正态分布曲线，称为正峭度。当标准差大于正常状态下的标准差，即观测值的分散程度较大时，峭度系数减小，此时曲线峰顶的高度低于正常正态分布曲线，称为负峭度。

2.2 融合EMD、峭度和Hilbert解调的诊断方法

滚动轴承故障振动信号中冲击成分所占比重较多，频率成分很丰富，在不同频带内所包含的轴承故障信息不同。当研究者分析滚动轴承振动信号时，经过EMD分解的各阶IMF分量会包含由故障引起的不同频段的固有振动成分［9-10］。依据峭度系数理论，峭度值较大的IMF分量中周期性冲击成分较多，即包含滚动轴承的故障信息越多［11］。因此，本研究选取原始振动信号经过EMD分解后峭度值较大几阶IMF分量重构信号，并将其作为Hilbert包络解调的对象，提取故障特征频率，与滚动轴承各个部件的理论故障频率对比，找出故障部位。因此，本研究采用下述分析步骤对滚动轴承进行故障诊断:

(1)对滚动轴承故障信号进行EMD分解，得到多个频率从高到低排列的IMF分量;

(2)根据式(10)计算各阶IMF分量的峭度系数;

(4)对重构信号进行Hilbert包络解调分析，得到包络信号;

(5)对包络信号进行FFT，获得信号的包络谱;

(6)参照滚动轴承各个部件的理论故障特征频率，对包络谱进行分析，根据谱上特征频率来判断轴承故障类型。

3 仿真信号分析

滚动轴承运行时，当外圈、内圈或者滚动体上发生磨损、点蚀、剥落等局部损伤时会产生突变的冲击脉冲力，该冲击作用会诱发轴承系统的高频固有振动成分，如轴承内外圈的径向弯曲固有振动、滚动体的固有振动或者测振传感器的固有振动等，导致在时域表现为简洁的周期性冲击信号被各种高频信号调制，形成较为复杂的调制信号。因此，本研究对该类信号进行包络解调处理，分析其特征频率将能够准确地辨识出滚动轴承的故障。

可以用如下数学模型描述滚动轴承内圈点蚀故障:

式中:fi—滚动轴承的内圈故障特征频率;fz—载波频率;Bcos(2πfi)—测试信号;A—一个直流分量，使偏置后的信号［A+Bcos(2πfi)］都具有正值;cos(2πfzt)—载波信号。

仿真程序随机生成滚动轴承内圈的故障特征频率和对应的高频载波频率，考虑实际工况下振动信号含有噪声，此处添加高斯白噪声信号n(t)。仿真形成滚动轴承内圈故障的振动信号为:

采用SPSS 21.00统计学软件对数据进行处理，计量资料以“±s”表示，采用t检验（血液流变学指标），计数资料以百分数（%）表示，采用x2检验（患者满意度），以P＜0.05为差异有统计学意义。

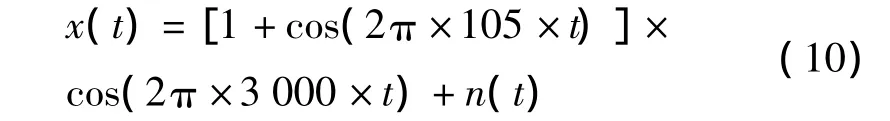
本研究设置采样频率为12 000 Hz，取持续1 s的仿真数据分析，对应的时域波形和频域波形如图1所示。由图1可以看出存在边频信号，虽然两者相减就是特征信号频率，但是在实际应用中，振动信号包含大量的干扰信号，其频谱图谱线较多，很难清晰地辨别出转频及其变频带，从而无法准确辨识出滚动轴承故障发生的部位。

图1 调幅仿真信号时域和频域波形图

本研究对x(t)进行EMD分解，得到12阶IMF分量。由于高斯随机白噪声的存在，仿真信号每次模拟时都会变动，导致各阶IMF分量的峭度系数会发生改变。但经过多次实验，发现前4阶高频IMF分量的峭度系数一直较大，现取前4阶IMF分量重构原信号，并对其进行Hilbert包络解调分析，解调后的谱图如图2所示。

图2 经Hilbert包络解调的重构信号频谱图

由图2可知，含有噪声的仿真信号经过EMD分解、选择性重组和Hilbert包络解调后，可以清晰地看出其频谱图有一条非常突出的谱线，且该谱线对应的频率刚好是滚动轴承内圈故障特征频率105 Hz。可见，融合EMD分解、峭度指标和Hilbert包络解调的分析方法能够很好地提取滚动轴承的故障特征频率，具有一定的实际应用价值。

4 滚动轴承故障诊断实例分析

本次使用的故障数据取自美国Western Reserve University电气工程实验室的滚动轴承故障模拟实验台的滚动轴承数据。该实验台由一个1.5 kW的电动机，一个扭矩传感器/译码器，一个功率测试计，还有电子控制器构成。待检测的轴承支撑着电动机的转轴，驱动端轴承为SKF6205深沟球轴承。轴承的局部损伤为电火花加工的单点损伤。采样频率为12 000 Hz，轴承转速为r=1 750 r/min［12］。

查阅手册可得SKF6205深沟球轴承的标准参数，通过理论公式计算可得轴承内圈的理论故障特征频率为157.9 Hz。驱动端滚动轴承内圈故障的时域波形如图3所示，采样点数12 000。

图3 滚动轴承内圈故障的时域波形

本研究利用融合EMD分解、峭度指标和Hilbert包络解调的分析方法对原始振动信号进行处理。EMD分解后得到的12阶IMF分量c1～c12和残余分量res如图4所示。

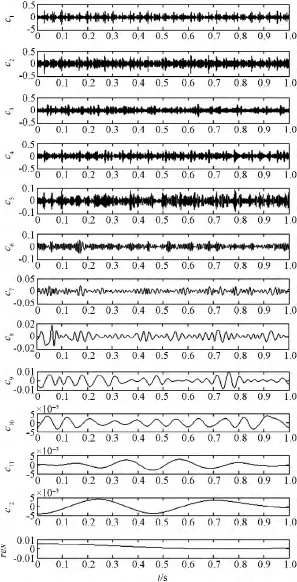
图4 轴承故障振动信号的第1～12阶IMF和res分量

各阶IMF分量的峭度值如表1所示。

表1 各阶IMF峭度值

从表1中可以看出，前4阶IMF分量的峭度值较大，相对而言其包含的故障信息最大，对前4阶IMF分量进行叠加重构原信号，并对重构信号进行Hilbert包络解调处理，其包络谱如图5所示。从图5中可以较为清晰地看出，包络谱中出现了滚动轴承内圈故障特征频率的1倍频(158 Hz)、2倍频(316 Hz)、3倍频(473 Hz)等，其中谱线在频率29 Hz处为轴承的转频。从上述分析可以确认该滚动轴承内圈发生故障，与实际相符。因此，本研究所提出的基于EMD和峭度指标的Hilbert包络解调分析方法能够应用在滚动轴承故障中。

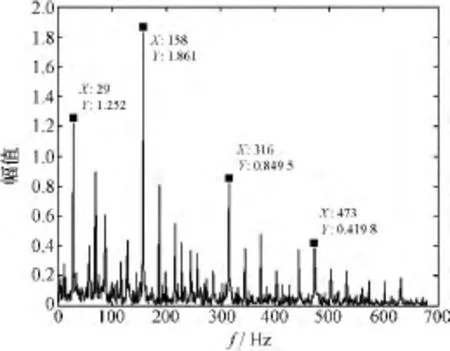
图5 重构的包络谱(局部放大图)

5 结束语

EMD分解能将非线性非平稳振动信号分解为多个能够反映原始信号局部特征的固有模态函数IMF，通过对部分IMF分量重构分析，能够清楚地揭示信号中包含的故障信息。Hilbert包络解调能有效地将故障特征信息从复杂的调制信号中提取出来，有效地排除了各种高频干扰、提高信噪比。

本研究提出了基于EMD和峭度指标的Hilbert包络解调分析的信号处理方法，并将其应用于滚动轴承故障诊断。笔者通过对仿真信号与实测信号的应用，清晰而准确地得到了滚动轴承的故障特征信息，表明了该方法可以较好地用于滚动轴承故障信号处理，为滚动轴承的故障诊断提供了一种有效的方法。

［1］钟秉林，黄 仁.机械故障诊断学［M］.3版.北京:机械工业出版社，2007.

［2］李 力.机械信号处理及其应用［M］.武汉:华中科技大学出版社，2007.

［3］胡清忠，褚福磊.基于Hilbert解调的滚动轴承故障诊断分析［J］.振动与冲击，2010，29(S):1-3.

［4］焦卫东，朱有剑.基于EMD与倒谱分析的轴承故障诊断［J］.机电工程，2009，26(2):18-21.

［5］张梅军，曹 勤，王 闯.EMD分解，分形理论和RBF神经网络相结合的轴承智能故障诊断研究［J］.机械，2012(11):16-21.

［6］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for non-linear non-stationary time series analysis［J］.Proceedings of the Royal Society，1998(454):903-995.

［7］宋晓美，孟繁超，张 玉.基于包络解调分析的滚动轴承故障诊断研究［J］.仪表仪器与分析监测，2012(1):1-4.

［8］LI Hui，ZHANG Yu-ping，ZHENG Hai-qi.Hilbert-Huang transform and maginal spectrum for detection and diagnosis of localized defects in roller bearing［J］.Journal of Mechanical Science and Technology，2009，23(2):291-301.

［9］朱 瑜，王 殿，王海洋.基于EMD和信息熵的滚动轴承故障诊断［J］.轴承，2012，15(6):50-53.

［10］施国友.滚动轴承对螺杆压缩机运行的影响［J］.流体机械，2012，40(7):35-36.

［11］YANG YU.Roller bearing fault diagnosis method based on EMD［J］.China Mechanical Engineering，2004，15(10):908-920.

［12］The Case Westren Reserve University Bearing Data Center Website.Bearing data center seeded fault test data［EB/OL］.［2007-01-01］.http://www.eecs.case.edu/laboratory/bearing.