基于改进型采样点卡尔曼滤波的矿用电池SOC估计

何灵娜，王运红

(浙江工业大学信息工程学院，浙江 杭州 310023)

0 引 言

矿用电池作为紧急避险设施、检测通信系统和井下运输车辆等煤矿工业设备的动力源，其荷电状态(SOC)估计的准确性与避难人员的安危密切相关[1]。目前，常用的电池SOC估计方法有开路电压法、Ah计量法、模糊神经网络法和卡尔曼滤波法等[2-5]。由于矿用电池的初始SOC值难以确定，且电池SOC在电池工作过程中易受多种因素干扰[6]。而扩展卡尔曼滤波(Extended Kalman Filter，EKF)算法计算量适中，且具有克服初值误差和累计误差的能力，因此被广泛应用于非线性系统的状态估计[7]。由于EKF算法是利用泰勒级数展开，并截断高阶项来实现非线性系统的线性化，该算法只适用于低动态弱非线性系统。当算法的估计误差较大时，算法的滤波精度就会降低、不稳定，甚至发散[8]。

矿用电池是一个强非线性系统，针对EKF只适用于连续可微的弱非线性系统且必须计算复杂的Jacobian矩阵[9]，基于采样点卡尔曼滤波算法(sampling point kalman Filter，SPKF)，本研究通过采用加权统计线性回归法实现模型函数统计线性化，从而在克服EKF缺陷的同时，实现电池SOC估计。本研究针对有限的电池管理系统资源，基于电池模型状态方程线性的特征，通过将标准KF和SPKF组合使用，从而实现算法运算量的降低。由于SPKF需要进行状态误差协方差开方，易于引起病态矩阵问题，本研究在SPKF算法中引入奇异值分解，并用特征协方差阵代替均方估计误差协方差阵。此外，本研究针对矿用电池外特性呈高动态非线性且电池模型误差不可避免，基于强跟踪原理，引入次优渐消因子。

1 矿用电池状态观测复合模型

状态观测复合模型将电池SOC作为非线性系统的唯一状态变量，因此计算复杂度低。该模型之所以被称为复合模型，是由于该模型由3种简单电化学模型复合得到[10]。

Sherpherd模型:

Unnewehr universal模型:

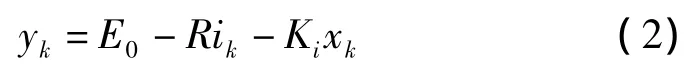
Nernst模型:

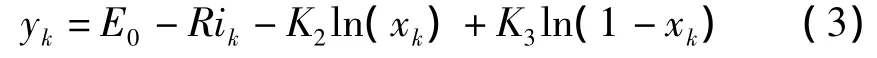
式中:xk—电池在k时刻的SOC值;E0—矿用电池的开路电压;R—示电池内阻;ik—k时刻电池的瞬时电流(电池放电时，ik—正;充电时，ik—负);yk—电池工作电压;K1，K2，K3—系统模型的匹配系数，其所在项表示电池极化内阻。

针对矿用电池SOC受环境温度和充、放电倍率影响较大的问题，本研究在复合模型中引入环境温度比例因子和充、放电倍率比例因子，并将其作为该算法的输入uk，而将易于直接测量的电池端电压作为电池模型的输出yk。由此得到，电池状态观测复合模型的表达式如下所示:

状态方程:

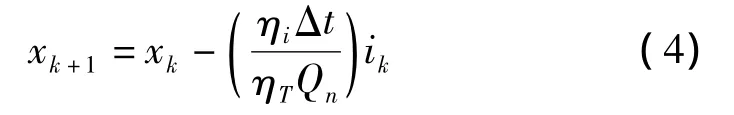
观测方程:

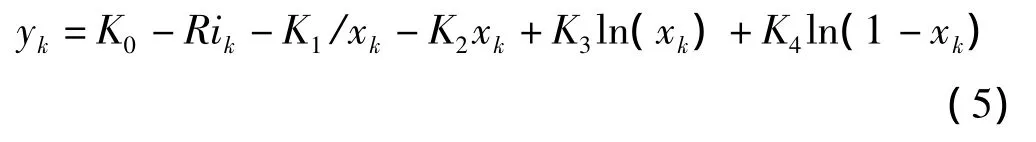
式中:K0—电池开路电压;ηi—额定温度下，放电电流为ik时的充放电倍率比例因子(在额定放电倍率下，ηi=1);ηT—额定放电倍率下，温度为T时的环境温度比例因子(在额定温度下，ηT=1);Qn—电池的额定容量。

电池状态观测复合模型作为Shepherd模型、Unnewehr universal模型、Nernst模型以及Ah模型的复合体，在性能上要远远优于其中任意一个电池模型。

2 基于改进型采样点卡尔曼滤波的电池SOC估计

矿用电池是一个高动态强非线性系统，为了获取实时、有效、精确的矿用电池SOC值，本研究基于最优高斯近似卡尔曼滤波框架中的SPKF算法，通过采用加权统计线性回归法实现非线性系统函数统计线性化，克服了EKF算法只适用于弱非线性系统以及必须计算Jacobian矩阵的缺陷，且使滤波精度逼近三阶以上[11]。

2.1 运算量的改进

由于矿用设备资源有限，针对“矿用电池状态观测复合模型的状态方程为线性方程，而只有观测方程为非线性方程”的特性，本研究通过在SPKF算法的时间更新阶段引入标准卡尔曼滤波算法来进行状态变量、状态误差协方差以及观测变量的一步预测，而后续测量更新与SPKF算法一致[12]。为了方便，该算法简写为KSPKF。

在算法的时间更新阶段，KSPKF算法只需要进行3步就可以完成，简单方便。笔者比较SPKF算法与KSPKF算法在时间更新阶段的运算量(乘法次数)，有关情况如表1所示。

观察表1可知，SPKF算法在时间更新阶段的运算量(乘法运算)为22n+7次，而KSPKF算法在时间更新阶段的运算量为10n+6次。可见，KSPKF算法在运算效率上得到了大大的提升。

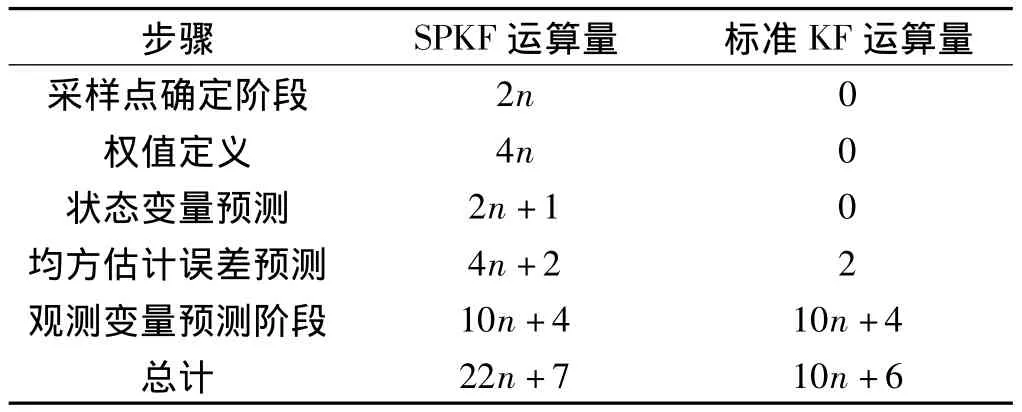
表1 SPKF和标准KF在时间更新阶段每步的运算量(乘法次数)

2.2 数值稳定性的改进

当KSPKF算法在进行采样点确定的过程中需要对误差协方差阵进行cholesky分解，而cholesky分解要求被分解矩阵必须满足正定性。

然而，矿用电池在工作过程中，由于物理因素以及环境因素引起的干扰的存在而使得采集误差不可避免。此外，对于含有误差的采集数据进行复杂的算法推导时，得到的结果又往往含有舍入误差，由此可知，误差协方差矩阵的正定性难以保证。

在SVD分解中，如果假定A∈Rm*n，m≥n，则SVD分解可以表示为:

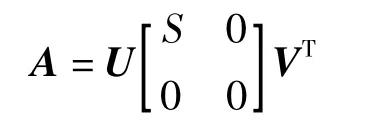
式中:U，V—A的左、右奇异向量;S—A的奇异值，S=diag{s1，s2，Λ，sn}，s1≥s2≥…≥sr≥0。

根据SVD分解的定义可知，SVD分解不仅不限制被分解矩阵的正定性，并且保证分解得到的奇异值都是正值[13]。因此，本研究针对KSPKF算法的数值稳定性问题，对算法的采样点确定进行了改进，试图采用稳定性和精度较好的SVD分解来代替cholesky分解，用特征协方差矩阵来代替协方差矩阵，其中采样点确定部分的方程式将被修改为:

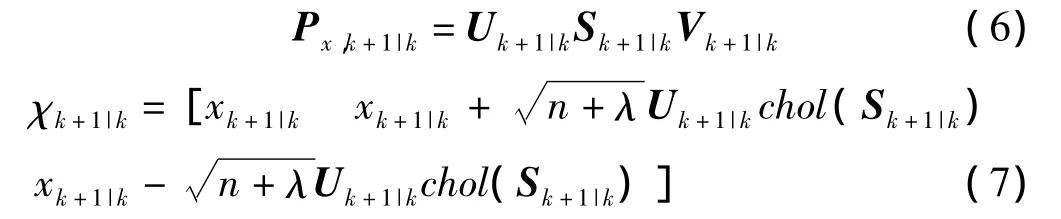
式中:λ=∂2(n+κ)－n;κ—比例因子，用于控制采样点与系统状态变量预测值xk+1|k点间的距离;n—系统状态维数;∂—采样点的扩散程度，通常满足:1e－4≤∂≤1。

为了方便，基于奇异值分解的SPKF算法在下面简写为SVD-KSPKF算法。

2.3 强跟踪原理的引入

对于矿用电池而言，噪声、部件磨损、老化等因素不可避免，因此要建立一个能够完全反映动力电池状态统计特性的精确模型十分困难。此外，矿用电池在工作过程中由于工作环境复杂，使得电池外特征参数变化较大，可见，本研究所设计的SOC估计算法不仅要有应对模型不准确的鲁棒性，还要能快速跟踪剧烈波动的电池端电流。然而，SVD-KSPKF算法对电池模型的依赖性很强，且当系统达到平稳状态时，SVDKSPKF算法增益阵Kk将趋于极小值;反之，当系统状态发生突变时，虽然预报残差有所增大，但增益阵Kk并没有随之迅速增大，而仍保持极小值。可见，该算法不具备快速跟踪突变状态的能力。对此，本研究在SVD-KSPKF算法中引入了强跟踪滤波器，并记为SSKSPKF算法。

强跟踪滤波器基于正交性原理，其基本思想是:在线选择适当的时变增益阵Kk，使得:

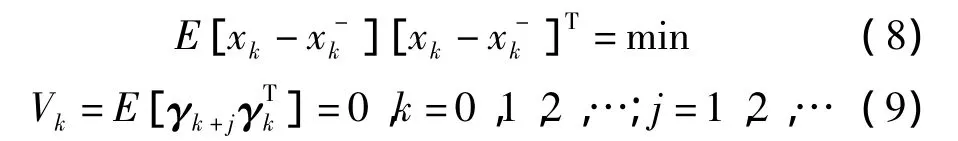
其中，式(8)是经典EKF的性能指标，式(9)要求不同时刻的残差序列处处保持相互正交。

本研究基于信息序列的正交性原理，在SVD-KSPKF算法中引入了次优渐消因子，其基本步骤如下:

首先，计算输出残差:

2.4 电池SOC估计算法设计

基于SPKF算法，本研究通过在时间更新阶段引入标准卡尔曼滤波原理实现算法运算量改进，并在此基础上引入奇异值分解和强跟踪原理，加强了算法的数值稳定性和跟踪突变状态的能力，且使其具有了抗模型误差的能力。其中，算法的递推过程如下:

(1)模型选择。

矿用电池内部化学反应复杂，汽车运行过程中易受物理振动、环境温度、测量误差等各种因素的影响。因此，本研究在上述观测方程和状态方程中引入了状态噪声和测量噪声，并将其表示为:

状态方程:

观测方程:

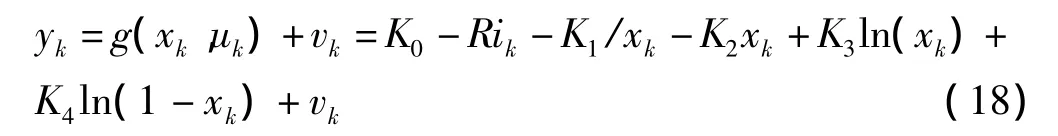
式中:wk—系统的状态噪声;vk—系统的测量噪声。

满足:

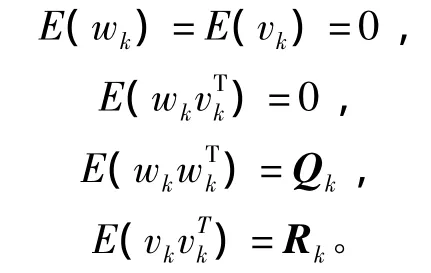
其中:Qk—系统状态噪声协方差阵，Rk—系统测量噪声协方差阵，E(.)—期望函数。

(2)初始化

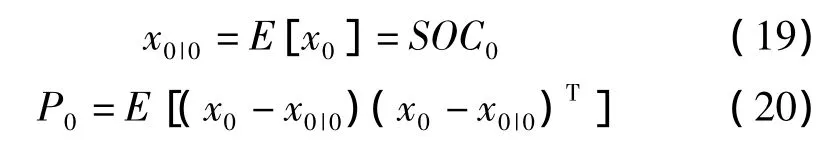
(3)状态变量和状态误差协方差的一步预测。

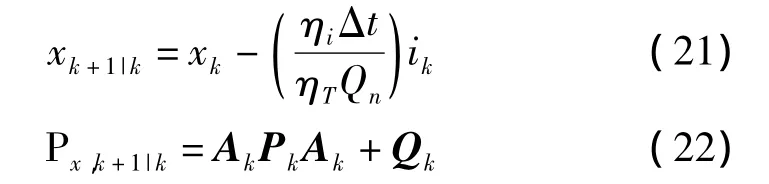
式中:Ak—系统动态特性的方程匹配系数，其取值为:Ak=1。

(4)观测变量yk+1|k的一步预测。

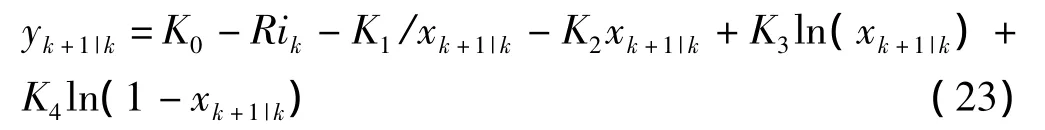
(5)次优渐消因子的引入。

其推导过程如公式(10～16)。

(6)奇异值分解及采样点确定。

其推导过程如公式(6～7)。

此外，与采样点对应的权值定义为:

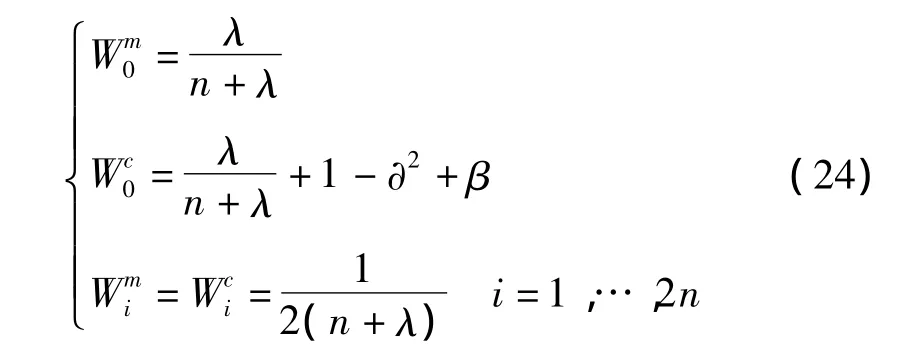
式中:β—状态分布参数。

(7)滤波增益阵的计算。

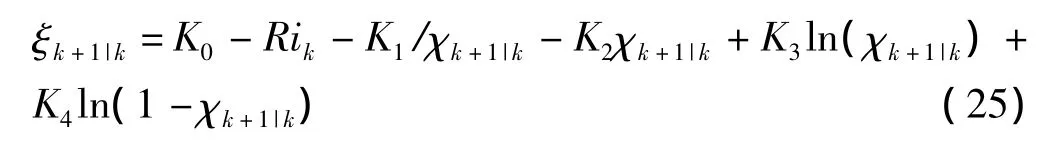
至此，若算法达到设定结束步数，则终止;否则，k=k+1，转向第(3)步，继续迭代循环。

3 实验分析

该实验选用的单体电池是型号为WX11U3215的磷酸铁锂聚合物动力电池，该电池的额定电压为3.2 V，额定容量≥15 Ah，额定放电电流为15 A，放电时的额定工作温度范围为－10℃ ～45℃[14]。其中，本研究所采用数据的实验对象为四节单体磷酸铁锂聚合物动力电池串联组成的电池组，由此可知，电池组的额定电压为12.8 V，额定容量为15 Ah。

为了更好验证所提出的改进算法应对模型误差的鲁棒性，本研究在算法模型输入参数K0中引入了随机噪声，其中，电池模型输入参数K0在引入随机噪声后的曲线图如图1所示。

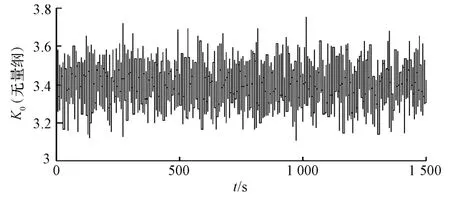
图1 电池模型参数K0加噪后的曲线图

此外，为了验证算法跟踪突变状态的能力，本研究通过在UDDS工况下对电池进行放电操作以模拟突变状态，并对电池端电流加入随机噪声以加大算法的模型误差。其中，加噪后的电池端电流波形图如图2所示。

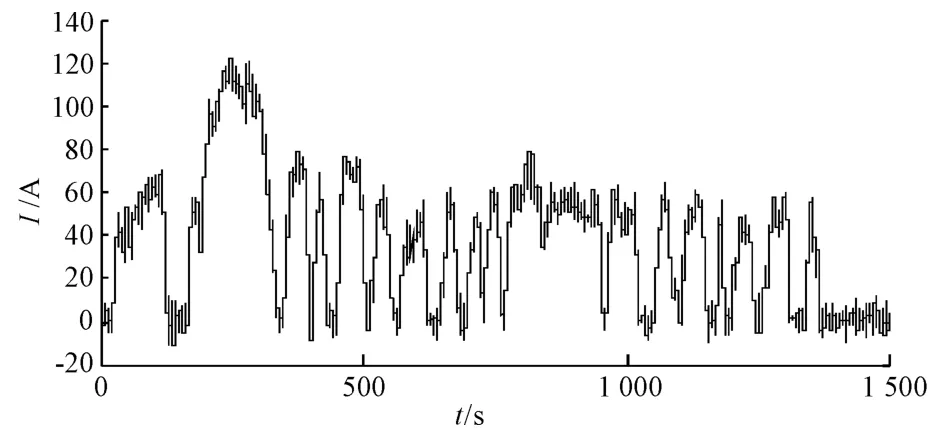
图2 加噪后放电电流波形图

为了更全面地验证所提出的算法的有效性，除了对SS-KSPKF算法进行了仿真实验外，本研究还对改进型EKF(在EKF中考虑了环境温度影响因子和充放电倍率影响因子)和SVD-KSPKF算法进行了仿真实验，以更全面地对算法估计结果进行比较分析。其中，电池SOC估计结果局部仿真放大图如图3所示。

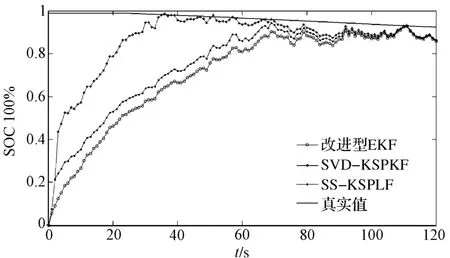
图3 电池SOC估计结果局部仿真放大图

观察图3可以发现，3种算法在大约80 s后均能较好地实现SOC值的准确估计。而在起初的0～80 s内，SS-KSPKF算法具有比SVD-KSPKF算法和改进型EKF算法更快的收敛速度和更好的收敛精度。可见，本研究提出的算法具有应对模型不准确以及跟踪突变状态的能力，很适合于矿用电池SOC估计。

4 结束语

本研究详细介绍了矿用电池状态观测复合模型，通过采用加权统计线性回归法，实现了非线性函数的统计线性化过程。针对电池复合模型的特殊性，将标准卡尔曼滤波算法与SPKF算法组合使用，减少了计算量。通过奇异值分解和强跟踪原理的引入，提出了改进型SPKF算法，并将其应用于矿用电池SOC估计。此外，本研究分析了改进型SPKF算法的递推过程，并进行了仿真验证。仿真结果表明:对于含有模型误差和状态突变的系统中，该算法依然具有较快的收敛速度以及较好的收敛精度。

综上所述，本研究提出的基于改进型的SPKF算法在保证了滤波精度和收敛速度的同时，还兼顾了计算量。可见，该算法可应用于矿用电池SOC估计。

[1]王沙沙，娄高峰，唐 霞，等.基于扩展卡尔曼滤波法的矿用可移动救生舱蓄电池荷电状态估计[J].工矿自动化，2013，39(2):43-47.

[2]江跃龙.基于UKF动力锂电池SOC动态估测方法与实现[D].广州:广东工业大学信息工程学院，2012.

[3]林成涛，陈全世，王军平，等.用改进的安时计量法估计电动汽车动力电池SOC[J].清华大学学报:自然科学版，2006，46(2):247-251.

[4]齐国光，李建民.电动汽车电量计量技术的研究[J].清华大学学报:自然科学版，1997，37(3):46-49.

[5]AFFANNI A，BELLINI A，CONCARI C，et al.EV Battery State of Charge:Neural Network Based Estimation[C]//IEEE International Electric Machines and Drives Conference.Medison:[s.n.]，2003:684-688.

[6]左适够，周 亚，张 达.基于DSP的电动汽车蓄电池电量计量及荷电状态估计[J].机电工程，2012，29(4):461-464.

[7]KALMAN R E.A new approach to linear filtering and prediction problems[J].Journal of basic Engineering，1960，82(1):35-45.

[8]赵 晓，汪 明，李晓明.改进扩展卡尔曼滤波算法在智能足球机器人比赛中的应用[J].机电工程，2012，29(3):334-338.

[9]PLETT G L.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs:Part 1.Background[J].Journal of Power sources，2004，134(2):252-261.

[10]HE H，XIONG R，GUO H，et al.Comparison study on the battery models used for the energy management of batteries in electric vehicles[J].Energy Conversion and Management，2012(64):113-121.

[11]LI J，KLEE BARILLAS J，GUENTHER C，et al.A comparative study of state of charge estimation algorithms for LiFePO4 batteries used in electric vehicles[J].Journal of Power Sources，2013，230(15):244-250.

[12]JWO D-J，LAI S-Y.Navigation integration using the fuzzy strong tracking unscented Kalman filter[J].Journal of Navigation，2009，62(2):303-322.

[13]LIU B，MA X-C，HOU C-H.A Particle Filter using SVD based Sampling Kalman Filter to Obtain the Proposal Distribution[C]//IEEE Conference on Cybernetics and Intelligent Systems.Chengdu:[s.n.]，2008:581-584.

[14]徐 杰.基于卡尔曼滤波的动力电池组SOC精确估计[D].杭州:杭州电子科技大学电子信息学院，2009.