Bouc-Wen土体动力模型的阈值应变研究

鲁丽雪，迟世春

（大连理工大学 海岸与近海工程国家重点实验室，辽宁 大连 116024）

1 引 言

土体的动力模型即动荷载下土体的应力-应变关系是表征土体动力学特性的基本关系，是土动力学研究的中心问题之一，也是分析土动力反应等一系列工程问题的重要基础。土体的动力特性主要表现出非线性、滞后性、变形累积以及强度与刚度退化特性。到目前为止，所提出土体动力模型大多不能令人满意。Bouc-Wen土体动力微分模型由Bouc[1]1967 年提出，Wen[2]和Baber等学者[3－4]对其进行了改进，使之能够模拟土体的强度和刚度退化特性。Bouc-Wen模型既包含非线性阻尼，又包含非线性刚度，可通过合理选择参数得到不同形状的滞回圈，用以描述土体在动力荷载作用下非线性、滞后性、变形积累以及强度与刚度退化等特性。Bouc-Wen土体动力模型也能很好地反映刚度和阻尼随剪应变的变化，适于描述多种类型土的循环动力特性。该模型还无需处理加载拐点，方便编程，具有良好的通用性。

图1为GDS动三轴试验得到的掺砾土心墙料滞回圈与Bouc-Wen模型滞回曲线的比较，可以看出，试验点与理论模型吻合良好。

国外学者已就Bouc-Wen模型的热力学可容许性开展大量研究工作，指出尽管Bouc-Wen模型独立于内时理论发展起来，但其仍属于基于内时概念的内部变量理论类模型[5－6]。由于某些应力路径引起负的能量耗散而可能违反热力学第二定律[7]。不过，单个滞回圈自动闭合而不发生应力或应变滑移，因此服从Drucker（或 Ilyushin）公设[8－9]。

Collins等[10]基于热力学基本原理建立了土体本构关系模型的方法，采用量纲分析，给出耗散函数的可能形式，对受力变形过程中的能量耗散机制等问题也进行了初步探讨。郭晓霞[11]、迟世春[12]等从热力学基本定律出发，对土体Hardin-Drnevich模型及 Ramberg-Osgood模型的增量耗散函数进行了构造，但由于采用了Masing准则假设，并未考虑实际阻尼比随剪应变的变化等。因此，有必要结合坝料的实际阻尼研究土石料动力变形机制。

本文以Bouc-Wen模型为研究对象，探讨其适用条件以及参数影响，从热力学基本定律出发，构造坝料的自由能函数和耗散函数，研究其耗散特征及动力变形机制，绘制其耗散应力空间和真实应力空间屈服曲线，探讨其屈服面的变化规律。

图1 理论滞回曲线与试验结果比较Fig.1 Comparison between theoretically predicted hysteretic loops and test results

2 Bouc-Wen模型耗散函数的构造

2.1 Bouc-Wen土体动力模型

Bouc-Wen土的动力模型的应力-应变关系为

式中：τ、γ分别为切应力和切应变；Gmax为最大剪切模量；α为屈服比，控制屈服后剪切刚度，取值范围(0,1)，主要影响滞回圈的面积。α越大，滞回圈越瘦，α对曲线的影响见图2。

图2 参数α 对滞回曲线的影响Fig.2 Influence of parameter α on hysteretic loop

参数ζ=ζ(t)是迟滞变量，用来控制土的非线性，由下列微分方程确定：

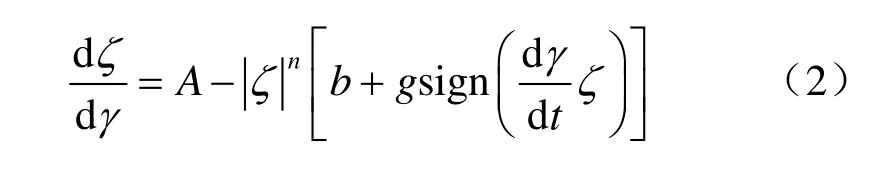
式中：A、g、b、n均为模型形状参数。

由式（1）、（2）可知，Bouc-Wen模型中加、卸载拐点由迟滞变量ζ和应变速率d/dtγ控制，无需特殊处理，这样可大大简化程序的编写。

A控制0ζ=时滞回圈的斜率，影响滞回圈的高度和面积。描述土的滞回特性时，A取值(0,1]，其单独变化时对滞回圈的影响见图3。

图3 参数A对滞回曲线的影响Fig.3 Influence of parameter A on hysteretic loop

g控制dγ/dt变号时曲线的刚度。为确保能量耗散值为正，应满足 g＞0，在此基础上具有物理意义的5种滞回圈分别是：①g+b＞0和g−b＞0（见图4）；②g+b＞0和g−b＜0（见图5）；③ g+b＞0和g−b=0（见图6）；④g+b = 0 和g−b＞0（见图7）；⑤g+b＜0和g−b＞0（见图8、9）。图2～9中 n = 1，Gmax=600000 MPa。

由图可知，当 g+b＜0 时滞回圈内凹，g+b＞0时滞回圈外凸，g+b = 0 时滞回圈呈拟线性。

图4 参数g对滞回曲线的影响Fig.4 Influence of parameter g on hysteretic loop

图5 参数b对滞回曲线的影响Fig.5 Influence of parameter b on hysteretic loop

图6 参数g+b对滞回曲线的影响(g-b=0,A=0.40)Fig.6 Influence of parameter g+b on hysteretic loop(g-b=0,A=0.40)

图7 参数g-b对滞回曲线的影响(g+b=0,A=0.50)Fig.7 Influence of parameter g-b on hysteretic loop(g+b=0,A=0.50)

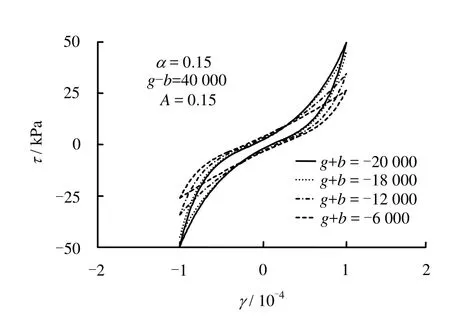
图8 参数g+b对滞回曲线的影响(g-b=40000,A=0.15)Fig.8 Influence of parameter g+b on hysteretic loop(g-b=40000,A=0.15)

图9 参数g-b对滞回曲线的影响(g+b=20000,A=0.10)Fig.9 Influence of parameter g-b on hysteretic loop(g+b=20000,A=0.10)

n为屈服指数，控制加载拐点初始加载阶段线性至非线性转换时的屈服前后滞回圈光滑程度，即屈服尖锐程度系数，n越小，过渡越平滑，其取值范围为0至无穷，n＞10时，近似理想弹塑性；n趋向无穷时，应力-应变曲线趋向双线性。n对单调加载曲线的影响见图10。

图10 参数n对滞回曲线的影响Fig.10 Influence of parameter n on hysteretic loop

2.2 模型耗散函数的构造

为确保模型不违背热力学定律，本文基于热力学基本定律构造了Bouc-Wen土体动力模型的增量耗散函数表达式。

假定塑性中心移动沿骨架曲线建立耗散函数，采用Ziegler正交条件，得到耗散应力空间中屈服函数的表达式。引入耗散应力及真实应力间的差别项，即迁移应力，得到真实空间中的屈服函数。由于Bouc-Wen模型的表达式是微分形式，为简化表达式，取n=1构造耗散函数。

滞回曲线统一表达为

骨架曲线为

式（3）与第1象限中骨架曲线走向相同的再加荷曲线g、γ1取负值，与第3象限中骨架曲线走向相同的卸荷曲线b取负值，与第3象限中骨架曲线走向相同的再加荷曲线g、γ1、b取负值；式（4）对于第3象限中骨架曲线g、b取负值，γ0为剪应变幅值，γ1为滞回曲线与横轴的交点，可由反对称性得出，下同。

综合公式（3）、（4）可得到塑性中心移动为即时骨架曲线时的耗散函数：

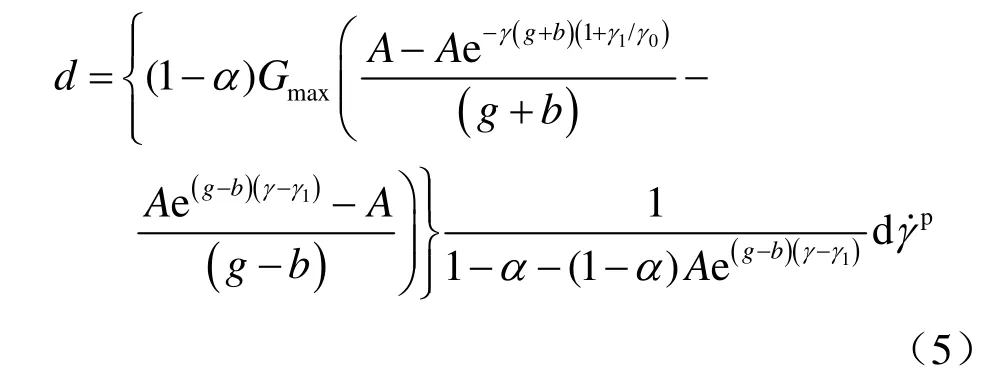
真实应力表达式为

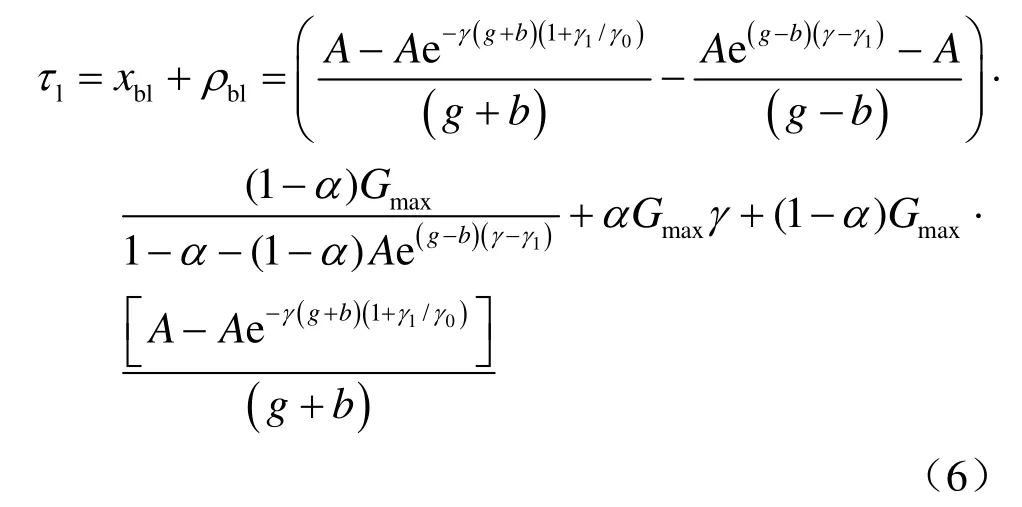
式中：xbl、ρbl分别为耗散应力和迁移应力，迁移应力，其公式为

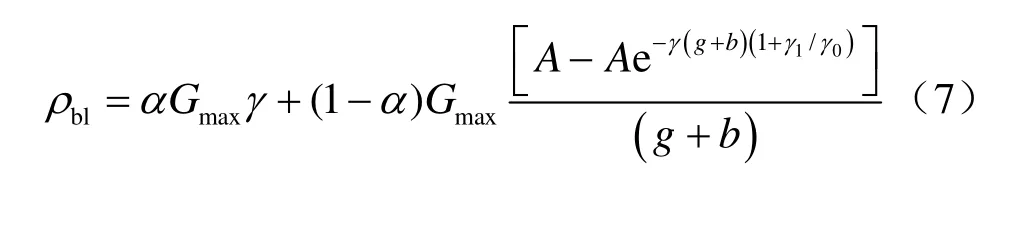
3 屈服曲线的绘制

结合某心墙坝工程选择粗堆石料、细堆石料及反滤料Ⅰ的动力试验成果，使用上述方法探讨其屈服面的变化规律。粗堆石料为角砾岩与花岗岩的混合物，细堆石料为弱风化以下花岗岩开挖料加工而成，二者采用大三轴动力试验机进行动力试验；反滤料I则为弱风化以下花岗岩加工而成，采用共振柱试验机及中型三轴仪进行动力试验。

3.1 最大动剪切模量

最大动剪切模量[13]由下式确定：

式中：Gmax为最大动剪切模量，σm为土体所受的初始平均静应力；pa为大气压力；k（与Gmax同量纲）、n1（无量纲）为试验常数，均由动力试验确定，筑坝粗堆石料、细堆石料及反滤料Ⅰ的模量系数k分别为2455.6、1303.9、976.0，指数 n1分别为0.6004、0.6109、0.4980。

坝料动剪模量比随动剪应变和阻尼比随动剪应变的变化见图11～13。

图12 细堆石料对应的模量衰减和阻尼增长曲线Fig.12 Corresponding modulus decline and damping growth curves of fine rockfill materials

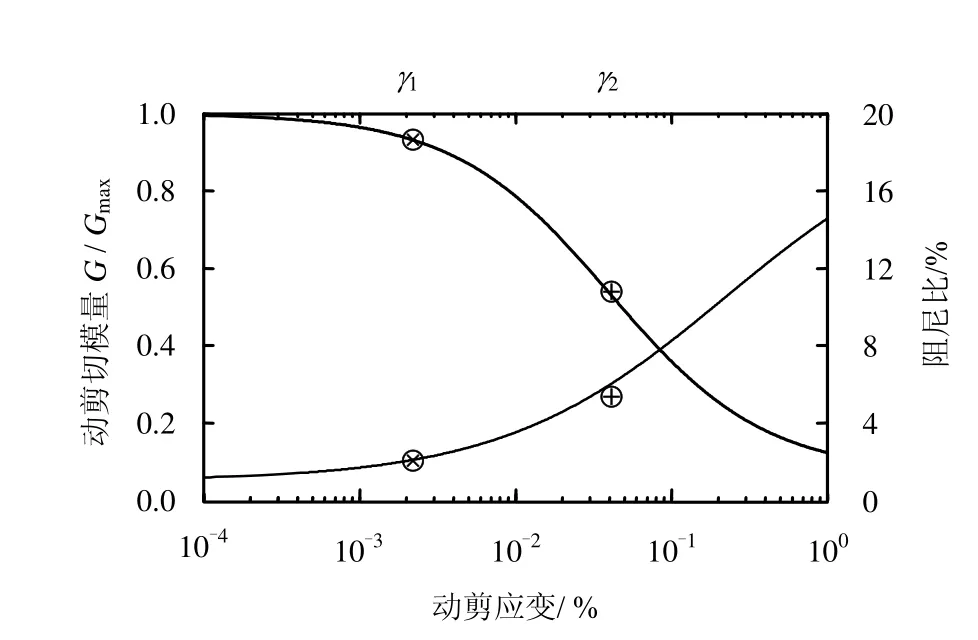
图13 反滤料Ⅰ对应的模量衰减和阻尼增长曲线Fig.13 Corresponding modulus decline and damping growth curves of the filter materialⅠ

3.2 Bouc-Wen模型参数辨识

根据动力试验提供的动剪切模量 Gs、等效阻尼比ξeq与动剪应变[14]的关系（见图11～13），用遗传算法对Bouc-Wen模型进行参数辨识。

遗传算法中选择算法采用比例选择方法，交叉采用非均匀算数交叉的方法，变异采用均匀变异，种群数量为80，迭代次数为1000，杂交概率为0.8，变异概率为0.1。由于参数n仅影响迟滞曲线的光滑度，取 n = 1，因此需辨识参数有α、A、g、b。

从模型参数识别的结果来看，随着动力水平的提高，阻尼增加，滞回圈变高、变胖，α、A、g−b、g+b 均逐渐降低。图14给出半对数坐标下粗堆石料对应的模型参数与动剪应变的变化规律。

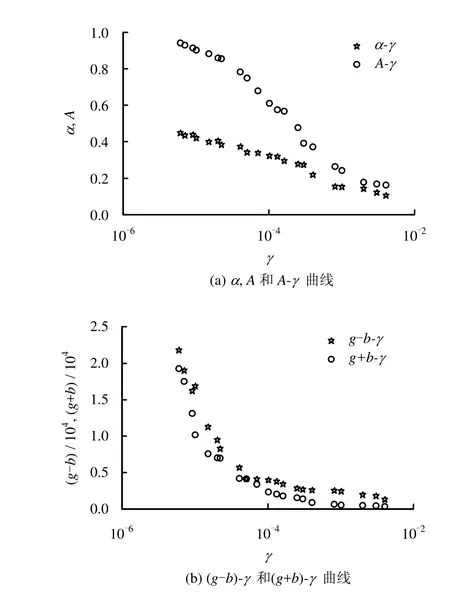
图14 参数α、A、g-b、g+b随剪应变的变化规律Fig.14 Variation trend of parameters α，A，g-b，g+b with the change of shear strain

在半对数坐标下拟合α-γ、A-γ、gb−-γ及g b+-γ曲线，得

3.3 屈服曲线的绘制

以粗堆石料为例，结合模量衰减和阻尼比增长建立Bouc-Wen模型，讨论p-q（单位为MPa）的应力空间中塑性中心的移动为骨架曲线时的屈服曲线的变化规律。随着γm不断增大，绘制屈服曲线如图15～17所示，其中（γm，τm）为滞回曲线的顶点。

图15 γm= 5×10-6时的屈服曲线Fig.15 Yield curves when γm= 5×10-6

图16 γm= 4×10-5时的屈服曲线Fig.16 Yield curves when γm= 4×10-5

图17 γm= 8×10-4时的屈服曲线Fig.17 Yield curves when γm= 8×10-4

图中分别绘制了γm=5× 10−6、4 × 10−5和8×10−4时试样的屈服曲线。由图可见，应变水平为5× 10−6时，不同γ/γm的屈服函数几乎为一条直线，滞回圈应变达到 4 × 10−5时，屈服面为斜率不同的直线。不同γ/γm的屈服面在p-q应力空间为同一直线说明土体屈服时土体颗粒之间的常摩擦系数起控制作用。因此，试样滞回圈应变在 5 × 10−6～4 × 10−5之间存在一个剪切屈服曲线的直线斜率，不再保持一致的界限应变，称之为第1阈值应变[15]，记为γt1。随着应变的增大，且达到 8 × 10−4时，屈服面已明显变弯。剪切屈服面弯曲代表控制堆石体试样塑性变形的机制除摩擦外，还有结构变化等机制。因此，试样滞回圈应变在 4 × 10−5～8 × 10−4之间存在剪切屈服曲线由直变弯的界限应变，称之为第2阈值应变，记为γt2[15]。

求出 3种坝料的阈值应变，并将其绘制于图11～13，得到第1、第2坝料阈值应变在Bouc-Wen模型对应的模量衰减及阻尼衰减情况。从粗堆石料及细堆石料的第1阈值应变所对应的归一化动剪切模量看，第1阈值应变对应的 G/Gmax在0.93～0.99之间，阻尼比为1%～4%。第2阈值应变对应的割线模量与最大动剪切模量之比范围为 0.54～0.79，与传统意义上以孔压开始升高或体积开始变化为标准定义的门槛应变相当。

4 结 语

本文探讨了Bouc-Wen土体动力微分模型的适用条件以及参数影响。从热力学基本定律出发，克服Hardin-Drnevich模型及Ramberg-Osgood模型未考虑实际阻尼比随剪应变变化的局限，结合模量衰减和阻尼增长给出基于Bouc-Wen微分模型的增量耗散函数，研究了筑坝土石料的动力耗散特征及动力变形机制，得到筑坝土石料的阈值应变。其中第二阈值应变与传统试验方法得到的门槛应变相当。

[1]BOUC R.Forced vibration of mechanical systems with hysteresis[C]//Proceedings of the Conference on Nonlinear Oscillators.Prague: [s.n.],1967: 315.

[2]WEN Y K.Method for random vibration of hysteretic systems[J].Journal of Engineering Mechanics Division,ASCE,1976.102: 249－263.

[3]BABER T T,WEN Y K.Random vibration of hysteretic systems[J].Journal of Engineering Mechanics Division,ASCE,1981,107(6): 1069－1086.

[4]BABER T T,NOORI M N.Random vibration of degrading,pinching systems[J].Journal of Engineering Mechanics,ASCE,1985,111(8): 1011－1027.

[5]CASCIATI F.Stochastic dynamics of hysteretic media[J].Structural Safety,1989,6(2－4): 259－269.

[6]SIVASELVAN M V,REINHORN A M.Hysteretic models for deteriorating inelastic structures[J].Journal of Engineering Mechanics,ASCE,2000,126(6): 633－640.

[7]CHARALAMPAKIS A E,KOUMOUSIS V K.A Bouc-Wen model compatible with plasticity postulates[J].Journal of Sound and Vibration,2009,322(4－5): 954－968.

[8]CAPECCHI D,DE FELICE G.Hysteretic systems with internal variables[J].Journal of Engineering Mechanics,2001,127(9): 891－898.

[9]ERLICHER S,BURSI O S.Bouc-Wen-Type models with stiffness degradation: Thermodynamic analysis and applications[J].Journal of Engineering Mechanics,2008,134(10): 843－855.

[10]COLLINS I F,HOULSBY G T.Application of thermomechanical principles to the modeling of geomaterials[C]//Proceedings of the Royal Society of London,Series A: Mathematical,Physical and Engineering Sciences.London: [s.n.],1997: 1975－2001.

[11]迟世春,郭晓霞,杨峻,等.土的动力 Hardin-Drnevich模型小应变特性及其阈值应变研究[J].岩土工程学报,2008,30(2): 243－249.CHI Shi-chun,GUO Xiao-xia,YANG jun,et al.Small strain characteristics and threshold strain of dynamic Hardin-Drnevich model for soils[J].Rock and Soil Mechanics,2008,30(2): 243－249.

[12]郭晓霞,迟世春,林皋.基于热力学定律的土体动力Hardin-Drnevich模型再认识[J].岩土力学,2008,29(9):2335－2340.GUO Xiao-xia,CHI Shi-chun,LIN Gao.Recognition of dynamic Hardin-Draevich model for soils based on generalized thermodynamics[J].Rock and Soil Mechanics,2008,29(9): 2335－2340.

[13]谢定义.土动力学[M].西安: 西安交通大学出版社,1988.

[14]王志良,韩清宇.黏弹塑性土层地震反应的波动分析法[J].地震工程与工程振动,1981,1(1): 117－136.WANG Zhi-liang,HAN Qing-yu.Sticky elastoplastic seismic response of soil layer wave analysis method[J].Earthquake Engineering and Engineering Vibration,1981,1(1): 117－136.

[15]郭晓霞.热力学方法在土体本构模型中的应用研究[D].大连: 大连理工大学,2009.