浅海低频声场水声信号时间相关性研究
2014-05-17张春华
于 倍,张春华,黄 勇,赵 闪
(1. 中国科学院声学研究所,北京 100190;2. 中国科学院大学,北京 100190)
0 引 言
水声信号在水下传播过程中,海水介质及其边界的不均匀性[1]会引起随机的声散射,反向散射同声源附近的接收器的声能叠加形成混响,前向散射的能量会导致接收信号幅度和波形的起伏变化。波浪会引起多途到达的信号的相对相位关系发生随机变化,从而导致在不同的时刻声源即使发出同样的信号,在固定的接收点收到的信号也会随时间而变化。
在起伏的海洋中,由于内波等海洋动力学过程[2]的存在,接收声场是时变的。水声信道中信号的时间相关特性是水声信号处理的理论基础和具体参数的选择依据。对水声信号的时间相关性[3]研究,一方面可找出补偿方案提高深度分辨、目标识别、数据融合的精准度;另一方面,线谱信号有较强的时间相关性,无论自相关或互相关均比海洋环境噪声强得多,可利用时间相关检测达到优良的抗噪声效果[4]。
1 信号时间相关的定义及特性
相关函数用于描述不同随机过程之间或同一随机过程内不同时刻取值的相互关系。相关运算分为自相关和互相关,互相关函数定义为:

对于自相关函数,只需以x (t)替换互相关函数中的y (t)即:

由于水声信号直接处理的都是实值信号,且经过采样成为能量有限的离散形式。所以,在工程应用中,提及的相关都是数字相关或相关序列。水声信号中的周期信号的自相关函数和原信号具有相同的周期,即rxx(m+M) =rxx(m)[5]。
在比较两个序列相似程度时,常常使用最小二乘法,旨在使序列x(n)和y(n)之间的线性相似程度最高,即相对误差能量最小。最小相对误差能量为

于是,定义相干系数为

扩展相干系数的定义,得到相干序列的定义:
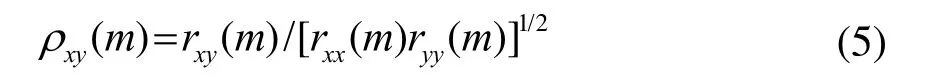
不难看出相干序列是归一化的相关序列。
声场的时间相关指的是水听器接收到的由稳定声源发出的信号在时间上的变化。声场中信号时间相关性强弱可以用其时间相关系数来定量表示。声源在不同的时刻发出相同的信号后,水听器接收到的信号分别是p(t)和p(t+τ),两个信号的时间相关系数定义为

归一化后得到

声场中信号相关系数是延迟时间τ的函数,声场时间相关系数下降到一定值时(一般取ρ(τ)下降3dB)对应的延迟时间τ0称为声场时间相关半径。
假设信号的变化主要由相位的变化引起,考虑线谱信号的相位率,窄带信号经过正交解调之后可表示为p(t) =R(t) eiϕ(t),其中R(t)是幅度,ϕ(t)是相位。

忽略幅度变化,有R(t+τ)≈R(t),自相关函数近似为其中:τ是延迟时间;ϕ'是信号相位对应的时间偏导(相位率);μ2是平均强度R(t+τ)R(t)≈μ2,把式(8)代入式(7),有ρ(τ) = e(−1/2)ϕ'2r2。由信号的时间相关半径定义求得:定义ϕ'=2πν,ν即是窄带信号的多普勒扩展,由上式可看出,多普勒扩展与信号的时间相关半径成反比。
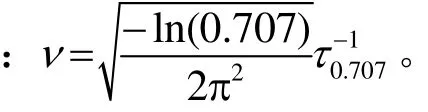
2 信号时间相关分析
在实际进行信号相关分析时,总是以有限的记录长度进行运算,在以有限的运算代替定义中无限时间的积分时,会产生误差。
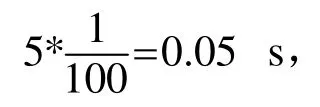
2.1 信号的自相关分析
单独分析均值为0、方差为1的高斯白噪声与带限白噪声的自相关函数如图1和图2、图3和图4所示,其中带限白噪声是白噪声通过fL=50 Hz、fH=200 Hz的带通滤波器产生的。
如图1所示,对应功率谱为σ2(仿真时σ2=1)的白噪声的自相关函数为rxx(m) =σ2δ(m)。

图1 高斯白噪声自相关分析Fig.1 The autocorrelation analysis of Gauss white noise
如图2所示的带限白噪声,其功率谱为一矩形波,因此自相关函数呈现sinc函数形状,m=0时有最大值,m足够大时趋近于零。

图2 带限高斯白噪声自相关分析Fig.2 The autocorrelation analysis of band limited white Gauss noise
分别对线谱信号及线谱信号叠加带限噪声进行自相关分析,如图3和图4所示,其中线谱频率为100 Hz,带限为50~200 Hz。由图可知,叠加带限噪声后,自相关的值比原线谱信号自相关值下降了很多,但其具有周期性,周期与线谱信号的周期相同。
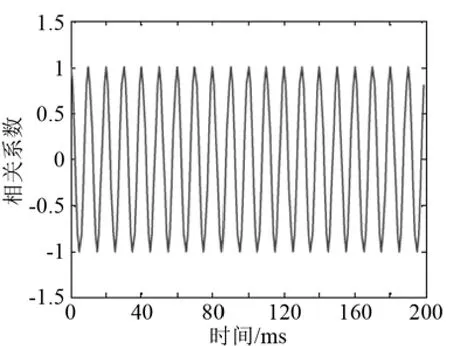
图3 线谱信号自相关分析Fig.3 The autocorrelation analysis of line spectrum signal
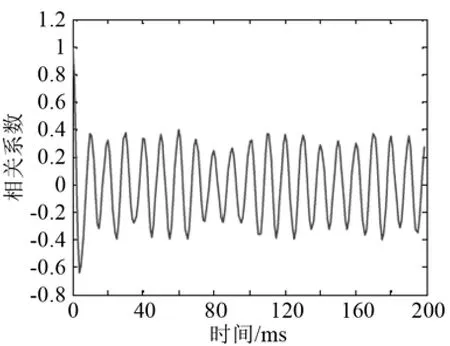
图4 线谱信号(100 Hz)叠加带限噪声自相关分析Fig.4 The autocorrelation analysis of line spectrum (100Hz) with stacked band-limited noise
进一步改变线谱频率为80 Hz,其它条件不变,分析如图5所示。线谱信号的频率不同,其自相关性分析仅表现为周期不同。通过分析可见,自相关分析对于不同频率、不同幅度的信号均使用,具有明显的抗噪声及整形作用。

图5 线谱信号(80 Hz)叠加带限噪声自相关分析Fig.5 The autocorrelation analysis of line spectrum (80Hz) with stacked band-limited noise
对信号较弱、背景噪声较强的信号做自相关性分析如图6和图7所示。在信号减弱时,自相关分析的数值降低很快,噪声的相关性成分会体现出来,但仍是以信号的相关性为主,且信号相关性仍是周期性变化的。
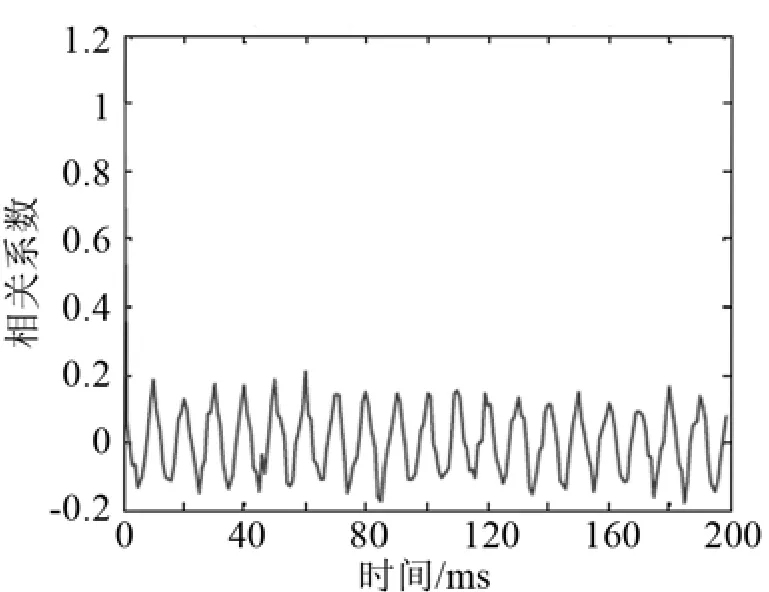
图6 低信噪比情况下线谱信号叠加高斯白噪声自相关分析Fig.6 The autocorrelation analysis of line spectrum with stacked band-limited noise(low SNR)

图7 线谱信号叠加高斯白噪声自相关分析(输入信噪比-10dB)Fig.7 The autocorrelation analysis of line spectrum with stacked band-limited noise (input SNR = −10dB)
上述分析可知,对于较强的信号,波形没有明显的失真,仍有强的时间自相关特性,说明自相关检测有较强的信道适应性,而且对于不同的工作频段,不同频点的自相关性不会因为频率改变而明显改变。而信号较弱时,噪声分量开始突出[7],此时虽仍有较强的相关性,但比强信号时下降了很多,可见自相关对于信号的强弱非常敏感。
2.2 信号的互相关分析
对仿真的接收信号分别做0.2、1 Hz的频移,且在0.2 Hz频移处与参考信号以及叠加噪声的参考信号进行比较,如图8、图9所示。1 Hz频点只与叠加噪声的参考信号进行比较,如图10所示。比较线谱信号自相关图3与频移0.2 Hz信号互相关图8,可看出相关系数略有降低。随着频移的增加,其互相关幅度明显下降,说明互相关要求参考信号与接收信号频率一致,当发生强烈的多普勒频偏漂移时,互相关检测可能失效。

图8 线谱信号频移0.2 Hz未叠加高斯白噪声互相关分析Fig.8 Cross-correlation analysis of line spectrum signal with a 0.2Hz frequency shift signal (no Gaussian white noise stacked)

图9 线谱信号频移0.2 Hz叠加高斯白噪声互相关分析Fig.9 Cross-correlation analysis of line spectrum signal with a 0.2Hz frequency shift signal (Gaussian white noise stacked)
3 低频水声场信号相关性仿真及验证
在基于时变的水声信道传播信号时间相关特性的仿真中,分别对400 Hz线谱和叠加噪声的400 Hz线谱进行互相关分析,得到图11、图12的特性曲线。
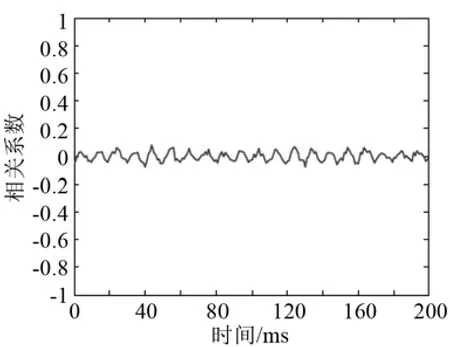
图10 线谱信号频移1 Hz叠加高斯噪声互相关分析Fig.10 Cross-correlation analysis of line spectrum signal with an 1Hz frequency shift signal (Gaussian white noise stacked)

图11 线谱信号400 Hz未叠加噪声时间相关分析Fig.11 Time correlation analysis of 400Hz line spectrum signal in underwater acoustic field without stacked noise
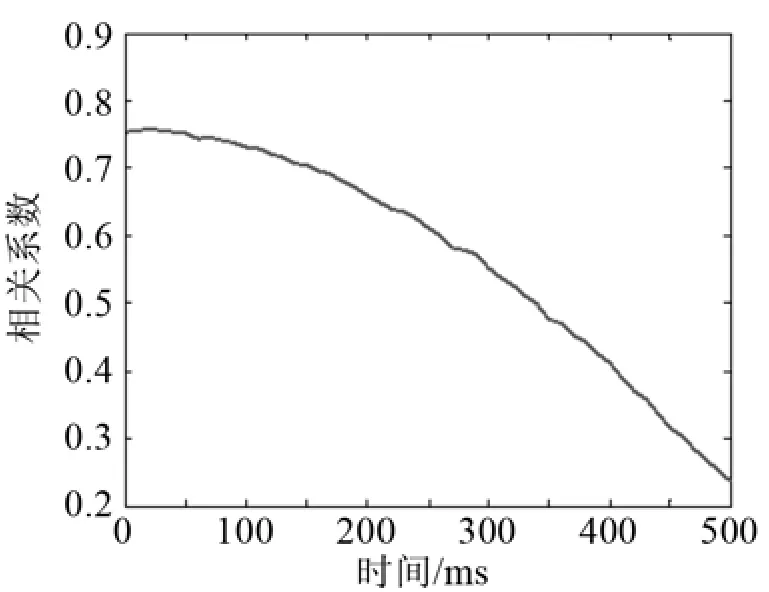
图12 线谱信号400 Hz叠加噪声时间相关分析Fig.12 Time correlation analysis of 400Hz line spectrum signal in underwater acoustic field with stacked noise
仿真验证不同频率信号在相同测试下的时间相关特性曲线,图13和图14分别为未叠加噪声与叠加−18 dB噪声的时间相关分析,可以看出,频率越低,其相干性越好,反映出水声信道随机扰动随着低频波长的增加而减弱。

图13 线谱信号未叠加噪声时间相关分析Fig.13 Line spectrum signal not stacked noise time-related analysis

图14 线谱信号叠加噪声时间互相关分析Fig.14 Time correlation analyses of different line spectrum signals in underwater acoustic field with stacked noise

图15 不同频率信号的时间相干性(海试实测)Fig.15 The temporal coherence of different frequency signals(measured form sea trial)
在实际海域进行试验,水深为70 m,声速剖面为负梯度。图15是在该低频浅海声场中接受到的不同频率信号的时间相干性曲线。可以看出,频率越低,相干时间越长,相干性越好,反映了信道随机扰动随着低频波长的增加而减弱,与仿真结果分析一致。
4 结 论
浅海声场中的水声信号传播受噪声干扰且具有随机时-空变化参数,波形畸变明显。本文研究浅海低频声场时间相关性以信号的自相关和互相关原理为基础,完成对信号时间相关半径、相关函数值的影响因素分析,得到不同声场条件下信号传播的作用结果。
研究表明在时-空变化参数的水声信道中进行相关性检测是有效的,可获得较高的抗噪声性能。仿真及实际海试数据验证得知,浅海低频声场随机扰动随低频波长的增加而减弱,且信号时间相关性研究为声场实际应用将提供一定参考依据。进一步工作将结合低频矢量探测,完成不同环境参数下目标深度的判别,在此基础上对多目标数据提取展开深入研究。
参考文献
[1] 李启虎. 声呐信号处理引论[M]. 北京: 海洋出版社, 2000: 96-100.LI Qihu. Sonar signal processing[M]. Beijing: Ocean Press, 2000:96-100.
[2] 蒋德军, 高天赋, 张云鹏, 等. 典型浅海温跃层内波对声场起伏的影响[J]. 声学学报, 1997, 22(3): 199.JIANG Dejun, GAO Tianfu, ZHANG Yunpeng, et al. The fluctuation of sound field due to internal waves on the thermocline in typical shallow water[J]. Acta Acoustics, 1997, 22(3): 199.
[3] 李启虎. 进入21世纪的声纳技术[J]. 信号处理, 2012, 28(1): 1-5.LI Qihu. Sonar technology in entering 21 century[J]. Signal Processing, 2012, 28(1): 1-5.
[4] 赵树杰, 赵建勋. 信号检测与估计理论[M]. 北京: 清华大学出版社, 2005: 36-61.ZHAO Shujie, ZHAO Jianxun. The theory of signal detection and estimation[M]. Beijing: Tsinghua University Press, 2005: 36-61.
[5] 袁兆凯, 隋天宇, 李宇, 等. 水声扩频通信中多普勒估计与补偿算法研究[J]. 电子与信息学报, 2012, 34(1): 51-56.YUAN Zhaokai, SUI Tianyu, LI Yu, et al. The estimation and compensation of Doppler effect on under water acoustic spectrum communication[J]. Journal of electronics & information technology, 2012, 34(1): 51-56.
[6] YANG T C. Measurements of temporal coherence of sound transmissions through shallow water[J]. J. Acoust. Soc. Am., 2006,120(5): 2595-2614.
[7] 曾庆勇. 微弱信号检测[M]. 杭州: 浙江大学出版社, 1994: 49-70.ZENG Qingyong. Weak signal detection[M]. Hangzhou: Zhejiang University Press, 1994: 49-70.
