小波阈值法在信号滤波中的应用研究

盛成明，唐锁夫，刘 超

(1. 海军702厂，上海 200434；2. 海鹰集团，江苏无锡 214000)

0 引 言

随着工程实践和理论分析的需要，经典傅里叶变换从不同角度衍生了诸如短时傅里叶变换、小波变换、分数傅里叶变换等理论。小波变换以其优越的时-频局部化分析能力在工程实践中得到了广泛应用[1,2]。小波变换通过从粗到细不断改变尺度，从而将研究对象的任何变换充分展示，近些年在信号滤波方面也取得了许多研究成果。小波域滤波通过小波变换方法对研究对象进行多层分解，由阈值函数对分解后得到的高频小波系数进行阈值量化，再由量化后的小波系数重构而得到真实信号的逼近。由此易知，阈值函数的选取对滤波效果将会产生直接影响。对于阈值函数的选取，大量研究人员也进行了一定的探索[3]。

本文通过对典型的阈值函数进行理论分析，提出了一种改进型的阈值函数，并和采用传统阈值函数的滤波效果进行对比。仿真结果表明，本文提出的改进型阈值函数在均方误差与信噪比方面都有一定改进。

1 小波阈值滤波原理

定义观测信号

其中：x(n)为原始信号，w(n)为噪声，且相互统计独立。

选择一个合适的小波函数，对y(n)进行N层分解，得到一系列小波系数[4]。由于在某些工程实际中，信号一般表现为频率较低或是平稳，而噪声通常表现为较高频率。通过小波多尺度分解产生的低频小波系数反映的是信号的逼近部分，高频系数反映的是信号的细节部分。因此，对第一层到第N层中的各层高频小波系数进行阈值量化得到估计小波系数，再通过小波逆变换实现信号的滤波，即信号的估计x1(n)[5,6]。具体实现方式如图1所示。

图1中，Aj为各层分解的低频系数，Dj为各层分解的高频系数。DDj为经过阈值函数量化后得到的高频系数，由图1可知，通过式(2)进行信号重构，即可实现信号的滤波。

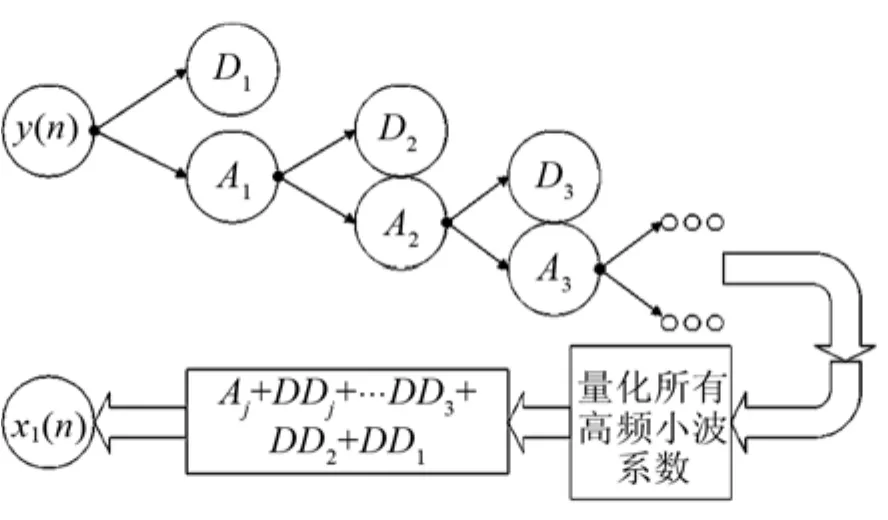
图1 小波阈值滤波实现方式Fig.1 Implementation method of wavelet threshold filtering

2 阈值函数的分析和改进

在小波系数阈值量化过程中，最具有代表性的阈值函数是硬阈值函数和软阈值函数，下面将通过硬阈值函数和软阈值函数的分析，给出改进型阈值函数。

2.1 硬阈值函数

设阈值为0＞λ，硬阈值函数定义为

即对自变量在阈值以下的函数值直接清零，阈值以上的函数值等于自变量的值。易知，函数在λ处不连续，且出现第一类间断点。

2.2 软阈值函数

软阈值函数定义如下：

其中sign(·)为符号函数，软阈值函数相当于对硬阈值函数曲线平移了λ个单位，实现了λ处曲线的连续。

2.3 改进型阈值函数

上述定义的软、硬阈值函数具有如下特点[7]：硬阈值函数在阈值处不连续，重构信号易产生振荡；软阈值函数的量化值与原始小波系数有恒定的偏差不能逼近。为了在一定程度上克服上述阈值函数的不足，本文构造一个新的阈值函数如下：

其中0＞α，为可变参数。

且f1(x) = 0 , (x= 0 )。因此，本文提出的新阈值函数既能在λ处连续，又能逼近原始小波系数。

2.4 三种阈值函数特点分析

为了更好地分析三种阈值函数的特点，图2给出了3种阈值的函数曲线，其中取0.1=α。

图2 三种阈值函数曲线Fig.2 Three kinds of threshold function curves

由图2易知，硬阈值函数对阈值以下的数值清零，满足小波阈值滤波的要求，但是函数在x=λ处不连续，出现了第一类间断点，因此对小波系数进行阈值处理后再重构的信号易产生振荡现象[8]，不利于含噪声信号的重构。

软阈值函数改善了硬阈值函数在x=λ处不连续、易引起重构信号振荡的不足，但由于软阈值函数对在阈值以上的小波系数也同样做了量化，且量化后的值与原始小波系数有一个恒定的偏差λ，不能够满足对小波系数的逼近，因此信号重构效果也并不好。

改进型的阈值函数对硬阈值函数的不连续性和软阈值函数的不能逼近性都进行了改善，同时，可变参数α可以根据实际情况进行调整，实现比硬阈值函数与软阈值函数更佳的滤波效果，因此应用将更加灵活。

3 信号滤波仿真分析

本文采用sym4小波，对信噪比为40 dB、幅值为10、频率为50 Hz的单频正弦信号进行3层分解，采样频率为2 kHz。其中噪声是方差为1的高斯白噪声。分别利用硬阈值函数、软阈值函数和改进型的阈值函数对各层高频系数进行阈值处理并进行信号重构。其中，α取0.1，阈值λ采用通用阈值[9]。

式中：σ为噪声的均方差；N为信号长度。三种阈值函数的滤波结果如图3所示。

图3 三种阈值函数滤波结果Fig.3 Filtering results of three threshold functions

由图3可知，三种阈值函数都有一定的滤波效果，但是三种阈值函数的滤波效果无法直观地进行对比，因此，定义如下参数：

其中：SNR为滤波后的信噪比，MSE为信号滤波后的均方误差[10]；x(n)为原始信号；x(n)为滤波后的重构信号。

为研究三种阈值函数在不同条件下的滤波效果，因此仿真时通过改变参数α以及信噪比以对比滤波效果，现将20 dB与10 dB时的滤波效果做如下对比，结果分别如表1、2所示。

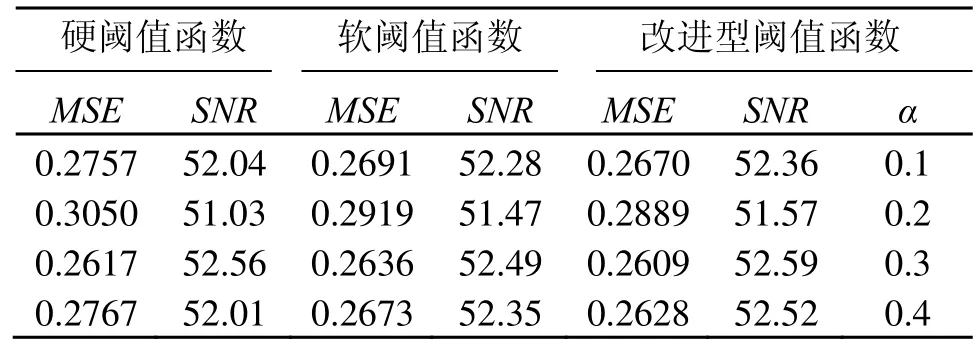
表1 20 dB条件下滤波效果对比Table 1 MSE and SNR of three threshold functions (20 dB)

表2 10 dB条件下滤波效果对比Table 2 MSE and SNR of three threshold functions (10 dB)

由表1、2可知，改进型的阈值函数无论是从MSE或者SNR都表现了良好的性能，在实际具体应用时，改进型的阈值函数可以灵活地通过改变参数α来改变滤波性能，而硬阈值函数和软阈值函数一旦确定阈值，便无法进行改变。

4 结 论

本文提出的改进型阈值函数，改善了硬阈值函数与软阈值函数的不足，通过对可变参数α进行调节，改进型阈值函数总能找到一个合适的α，使其在MSE和SNR方面优于硬阈值函数和软阈值函数。这对于需要同时考虑滤波效果以及波形失真度的应用场合则显得尤为有用。然而，由于改进型阈值函数中的参数α需要通过实验去确定最佳值，因此对于不确知环境的应用则尚有不足，需要进一步深入研究。

参考文献

[1] 冉启文, 谭立英. 小波分析与分数傅里叶变换及应用[M]. 北京:国防工业出版社, 2002.RAN Qiwen, TAN Liying. Wavelet analysis and fractional Fourier transform and its application[M]. Bejing: National Defence Industry Press, 2002.

[2] 邹红星, 周小波, 李衍达. 时频分析回溯与前瞻[J]. 电子学报,2000, 28(9): 78-84.ZOU Hongxing, ZHOU Xiaobo, LI Yanda. Retrospective and prospective time-frequency analysis[J]. Journal of Electronics,2000, 28(9): 78-84.

[3] Donoho D L. De-noising by soft thresholding[J]. IEEE Trans on Inform Theory, 1995, 41(3): 613-627.

[4] Donoho D L, Johnstone I M. Adapting to unknown smoothness Via Wavelet thrinkage[J]. Journal of American Stat Assoc, 1995,90(432): 1200-1204.

[5] 葛哲学. 小波分析理论与Matlab R2007实现[M]. 北京: 电子工业出版社, 2007.GE Zhexue. Wavelet theory and Matlab R2007 implementation[M]. Beijing: Electronic Industry Press, 2007.

[6] 高静怀, 汪文秉. 小波变换与信号瞬时特征分析[J]. 地球物理学报, 1997, 40(6): 821-832.GAO Jinghuai, WANG Wenbing. Wavelet transform and signal characteristics of transient[J]. Chinese Journal of Geophysics,1997, 40(6): 821-832.

[7] 张维强, 宋国乡. 基于一种新的阈值函数的小波域去噪[J]. 西安电子科技大学学报, 2004, 31(2): 296-299.ZHANG Weiqing, SONG Guoxiang. Signal de-noising in wavelet domain based on a new kind of thresholding function[J]. Journal of Xi- Dian University, 2004, 31 (2): 296-299.

[8] 王芳, 鲁顺昌. 小波软硬阈值去噪算法的研究及改进[J]. 信息技术, 2008(6): 124-127.WANG Fang, LU Shunchang. Study and improvement of hard and soft thresholding Wavelet algorithm[J]. Information Technology, 2008(6): 124-127.

[9] 叶重远, 黄永东. 小波阈值去噪算法的新改进[J]. 计算机工程与应用, 2011, 47(12): 141-144.YE Chongyuan, HUANG Yongdong. The new improved wavelet thresholding algorithm[J]. Computer Engineering and Applications, 2011, 47(12): 141-144.

[10] 付炜, 许山川. 一种改进的小波域阈值去噪算法[J]. 传感技术学报, 2006, 19(2): 534-540.FU Wei, XU Shanchuan. An improved wavelet thresholding algorithm[J]. Sensing Technology, 2006, 19(2): 534-540.