应用Poisson板理论求解S0兰姆波在通孔缺陷的散射

张海燕，姚杰聪，马世伟

(1. 上海大学通信与信息工程学院，特殊光纤与光接入网省部共建重点实验室，上海 200444；2. 上海大学机电工程与自动化学院，上海市电站自动化技术重点实验室，上海 200072)

0 引 言

因为兰姆波在(NonDestructive Testing, NDT)应用的潜力，近年来波导中的散射问题受到相当大的关注。由于其复杂性，所进行的研究主要是应用数值方法如有限元法(Finite Element Method, FEM)[1]或边界元法(Boundary Element Method, BEM)[2]。虽然二维(2D)研究能够部分洞察兰姆波与缺陷之间的相互作用，为了全面地理解散射过程，3D建模是必须的。尽管计算能力和效率不断提高，数值方法仍然需要相当高的计算代价。即使高性能计算机，对一个特定的入射波场，计算时间也是几个小时的数量级。而解析或半解析解对这样的问题是适用的，能够快速仿真众多不同散射体的散射。对于2D问题，解析解方法已用于研究兰姆波遇圆形腔体[3]或裂纹[4]的散射。对于3D问题，寻求解析解相当复杂。虽然瑞利-兰姆波解是精确的，然而，它在表征兰姆波与结构缺陷的作用时相当困难，因为在无限多的模式中，需要考虑模式耦合的影响[5-8]。即使激发频率低于第一阶模式的截止频率(也即仅有一个传播模式)，近场波高阶模式[9]在缺陷与周围结构的界面上也参与模式转换过程[10]。Grahn[6]采用双级数波函数展开法，给出了部分穿透孔的数值解，发现为了实现收敛，需要大量的兰姆波模式。例如，在第二个弯曲模式的1/3倍截止频率这样低的频率，计算中需要9个兰姆波模式[11]。对于更高的频率，在展开式中将会有更多项，这样将导致很慢的收敛率。因此，要求寻找计算上更有效的求解方法。

作为对兰姆波精确解的替代，各种近似板理论，如 Kane-Mindlin膨胀形变(extensional deformation)理论[12]以及 Mindlin板弯曲理论[13]，无论是对称和反对称模式，都已可以很精确地描述兰姆波的频散特性，达到了第二个弯曲模式的截止频率[14]。在低频限制下，对于膨胀波(S0波)，Mindlin板理论退化到 Poisson板理论，对于弯曲波(A0波)，Mindlin板理论退化到 Kirchhoff板理论。Mckeon和Hinders[15]采用Mindlin板理论，考察了S0波与各种尺寸孔的散射特征。对点源激发的 S0波，证实了当孔的尺寸大于波束尺寸时，散射的影响很重要，解释了铝板中大缺陷孔平行投影层析成像中存在星状条纹图案赝像的原因，文中的理论和散射求解方法对发展兰姆波衍射层析成像具有重要作用。

本文基于Poisson板理论，研究了入射的S0平面波与圆形通孔缺陷之间的相互作用。由于所考虑的问题是3D问题，散射场中也包含SH波。又因为入射场关于板中面是对称的，散射体也是对称的，在低频时，散射场中仅包含对称的S0和SH0模式，文中对这两种模态的散射特性进行了研究，并与Diligent的3D精确理论[5]进行比较。给出了这两个模式位移散射场的远场方向图，研究了激发频率和缺陷尺寸对散射结果的影响，希望能为兰姆波无损检测提供一些理论指导。

1 问题描述

考虑入射的 S0平面波遇到圆形通孔缺陷的散射。几何模型如图1所示，板的厚度为2h，通孔的半径为a，坐标系统原点位于通孔的中心。考虑时谐状态，省略时间因子exp(i)tω−，其中ω表示角频率，t表示时间。

2 Poisson板理论

2.1 基本方程

Poisson板理论是描述膨胀运动的低阶近似板理论。其位移场是由两个标量势场φ、ψ控制，在固定频率下，两者满足亥姆霍兹(Helmholtz)方程：

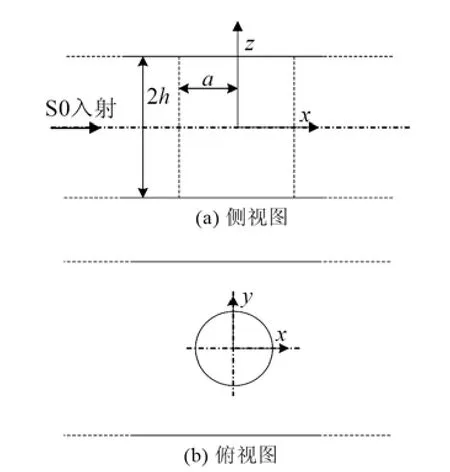
图1 含通孔板几何模型Fig.1 The geometry of plate with a through hole

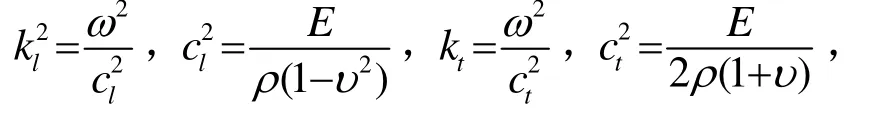
图2给出了Poisson板理论与3D精确理论频散曲线的比较。Poisson板理论的cl在低频时与S0模式重合，Poisson板理论的ct在整个频率范围内与SH0模式重合。在低于S1模式的截止频率(频厚积约为2.8 MHz·mm)，S0和SH0是3D精确理论中的传播模式，它们对波场的贡献最大，其它非传播模式(凋零波，波数为复数)相对于这两个模式对波场的贡献较小。因此，在与这两个模式重合的频率范围内，Poisson板理论可以作为3D精确理论的一种近似替代。

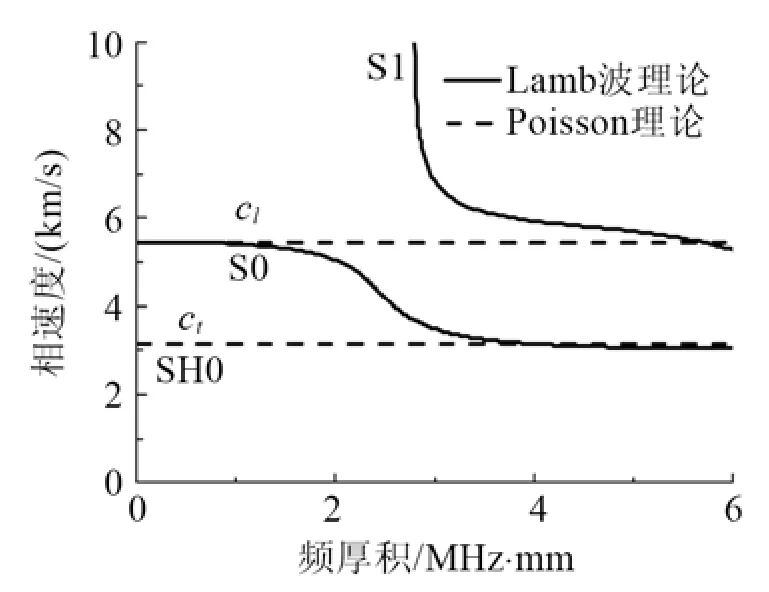
图2 Poisson板理论与3D精确理论频散曲线的比较Fig.2 Dispersion curves of the Poisson theory (dash lines) compared to the exact 3D theory (solid lines)

柱状坐标下的应力和应变可表示为[6]：

式(3)中的位移用势函数表示为

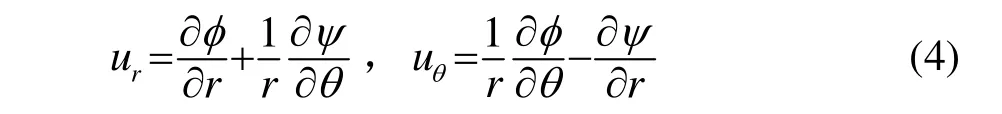
结合式(2)~(4)，可得：

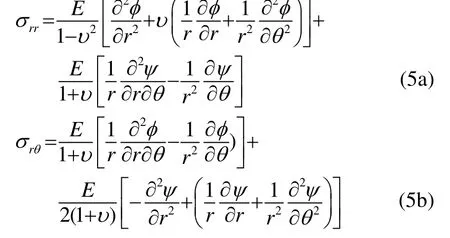
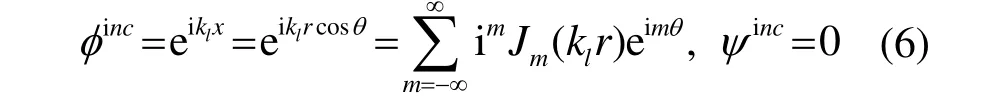
2.2 波场展开

S0平面波入射时，入射场用势函数表示为：

将式(6)代入式(5)，可得

在散射场区域，方程(1)的解为

am与bm为散射场的展开系数，可利用在缺陷处的边界条件求出。

将式(8)代入式(5)，可得

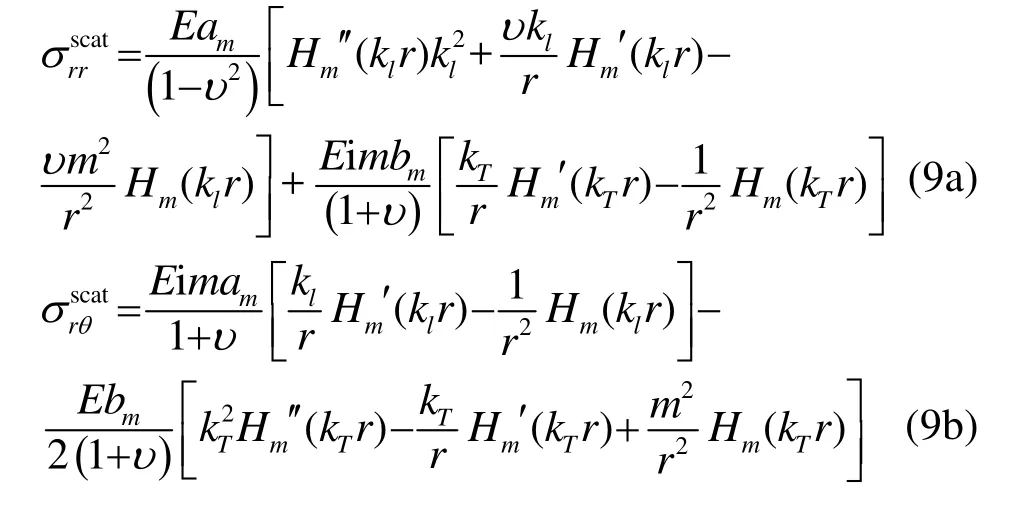
2.3 边界条件

同3D精确理论类似，在孔边缘r=a处的边界条件为：

方程(8)中的展开系数可通过式(10)确定。对每一个m值，含有两个未知数的系统方程用矩阵形式表示为

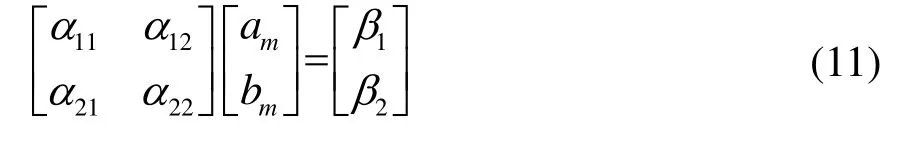
式(11)中的αi,j(i,j=1,2)、βi(i= 1 ,2)见后面附录。

3 数值计算

数值示例中所用的材料为刚板，其材料参数为：杨氏模量E=210GPa，泊松比υ=0.3，或Lamé常数λ=121.2 GPa，μ=80.8 GPa，密度ρ=8100 kg/m3。

数值分析中的无量纲参数为：入射场的波数k与孔半径的乘积ka(k为入射的S0模式的波数，这里k=kl)，归一化频率Ω=ωh/ct，孔半径a/h。

文献[5]给出了Poisson板理论和Diligent的3D精确理论在不同频率、不同孔径时两种基本对称模式的位移远场散射方向图，并对其结果进行了比较。散射波的位移远场幅值定义为

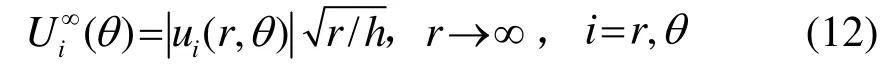
3.1 频率变化对散射场的影响

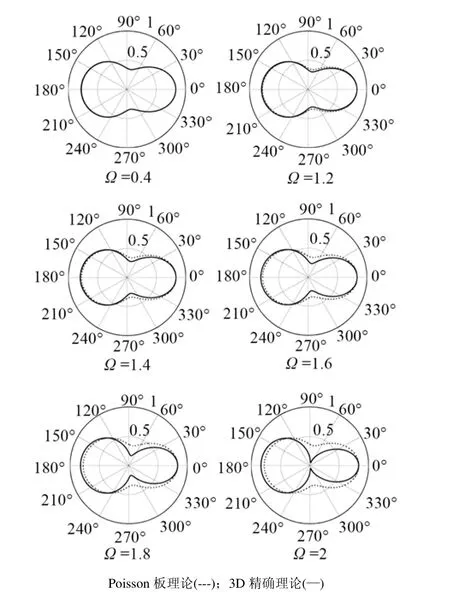
图3 不同频率时S0模式的位移散射远场方向图Fig.3 Far field patterns of displacement scattering for S0 mode at different frequencies

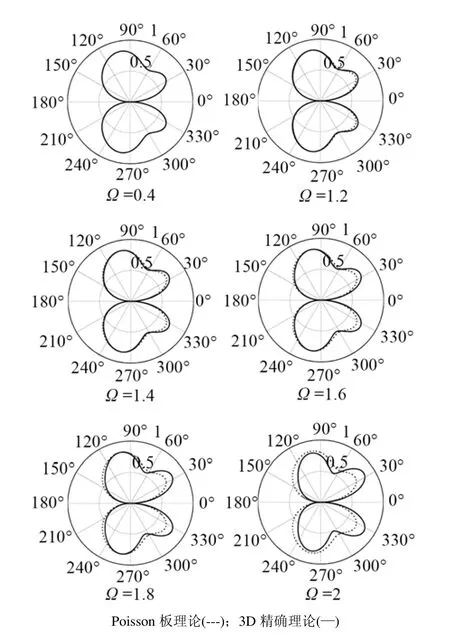
图4 不同频率时SH0模式的位移散射远场方向图Fig.4 Far field patterns of displacement scattering for SH0 mode at different frequencies

图3和图4给出了S0和SH0的位移散射远场方向图，其中，ka=1(a≈λ/6，λ为入射波的波长)。可以看到，随频率(更确切地说，频厚积)增加，Poisson板理论偏离3D精确理论的变化情况。低频时，Ω≤0.4，两个理论模型具有完好的一致性。随着频率增加，两者间逐渐分离，当Ω=1.2时，Poisson板理论与3D精确理论的偏差较小。但随着频率继续增大，Poisson板理论在形状上与3D精确理论的差异逐渐增大。对不同的孔径，如ka=2(a≈λ/3)，随着频率变化，这两个理论具有类似的变化趋势，只不过它们出现偏离时的频率可能不同，这里不再给出。

3.2 缺陷尺寸对散射场的影响

既然Poisson板理论在低频情况下可以作为3D精确理论的替代，我们可以在低频时采用 Poisson板理论研究散射体(缺陷)变化对散射场的影响，以便对缺陷进行评价，这将大大简化计算。图5和图6给出了Ω=0.4，不同ka值时的S0和SH0模式的位移散射远场方向图。可以看到，散射的 S0波主要集中在前向(0°)和后向(180°)(图5)，而散射的 SH0波主要集中在横向方向(90°~150°,210°~270°)(图6)。随着ka增大，S0波越来越集中在前向，且具有更强的波束指向性和更大的幅值(图5)。同样，随ka增大，SH0波在横向方向也具有更大的幅值(图6)。更清晰的比较显示在图7中，可以看到，0°散射角时的S0散射波幅值可以反映ka的变化，而110°(或 250°，由于对称性，图中未给出)附近散射角时SH0散射波的幅值也可以反映ka的变化，且这种变化近似线性，如图7(b)、7(d)所示，以此可以对缺陷的大小进行评判。

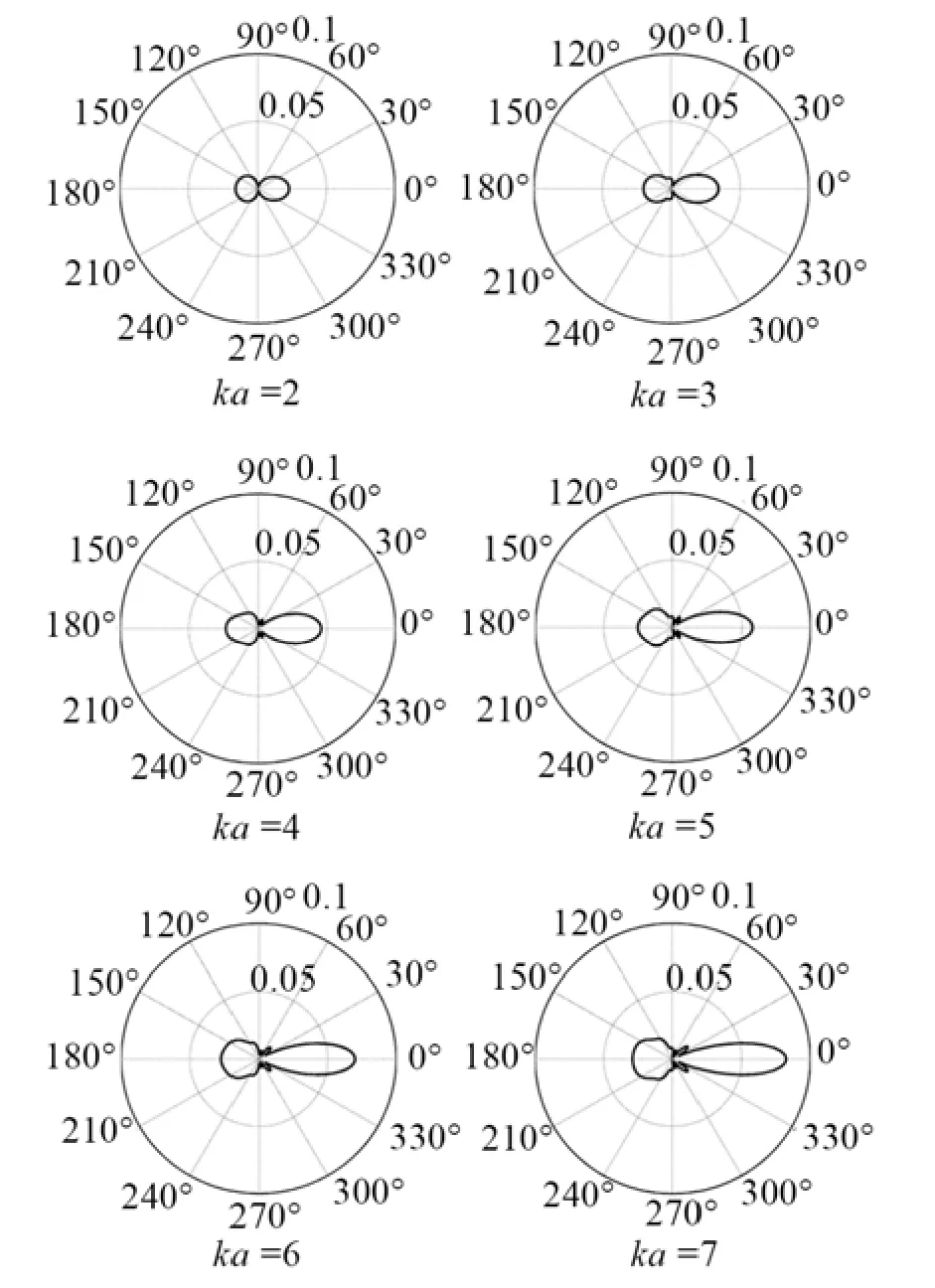
图5 Ω=0.4，不同ka值时S0模式的位移散射远场方向图Fig.5 Far field patterns of displacement scattering for S0 mode at Ω= 0 .4 for different ka values

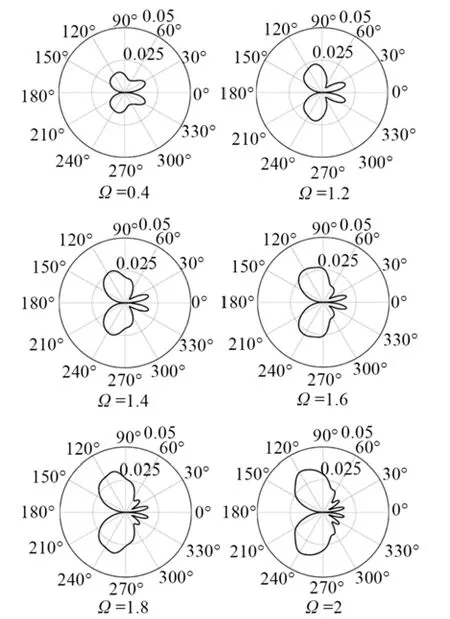
图6 Ω=0.4，不同ka值时SH0模式的位移散射远场方向图Fig.6 Far field patterns of displacement scattering for S0 mode at Ω= 0 .4for different ka values

图7 Ω =0.4，不同ka值时S0和SH0模式的散射图Fig.7 Scattering patterns of S0 and SH0 modes for different ka values atΩ=0.4

4 结 语

尽管3D精确理论在高频情况下求解散射场比较精确，但是其计算过程繁琐，并且随着频率的增高，模态数变多，计算复杂性变大。在低频情况下，采用3D精确理论并没有显示出优越性。基于此，本文用简单的Poisson板理论计算S0兰姆波对通孔的散射，并与 3D精确理论进行了对比，给出了Poisson板理论的适用范围。在此基础上，对S0和SH0的远场散射特性进行了研究，得出的结论是：

(1) Poisson板理论是最低阶的描述膨胀波运动的近似板理论，仅在低频下(如对钢板，Ω≤0.4，相当于频厚积≤0.4MHz·mm)才可以给出较精确的结果。

(2) 在低频限制下，Poisson板理论相比3D精确理论是一种较好的选择，可以极大地简化计算。这是因为3D精确理论波场展开式中包含较多的传播模式和非传播模式，而 Poisson板理论仅含有两个模式。实际上，为了避免兰姆波的频散和多模式混叠，兰姆波检测多在低频情况下进行。

(3) S0和SH0具有不同的散射场分布。S0散射波能量主要集中在前向和后向，其前向散射波幅度随孔径增大线性增加。SH0散射波能量主要集中在横向方向，在某些散射角度方向散射波幅值也随孔径呈近似线性变化。这两种模式都可以为缺陷无损评价提供理论指导。

(4) 本文所用的理论和方法为用解析法求解兰姆波在固体中的散射提供了基础。从入射场来说，可以推广到任何可能的波型，如更高阶的对称模式、弯曲波模式(反对称模式)，也可以从平面波入射推广到点源、有限宽度的源入射。从缺陷类型来说，可以从通孔推广到盲孔，也可以从圆孔推广到椭圆孔，甚至不规则孔。从材料来说，也可从各向同性材料推广到各向异性复合材料。

参考文献

[1] 郑阳, 何存富, 周进节, 等. 超声兰姆波斜入射裂纹时的散射特性[J]. 机械工程学报, 2013, 49(4): 6-12.ZHENG Yang, HE Cunfu, ZHOU Jinjie, et al. Scattering characteristic of Lamb wave at crack with oblique incident[J]. J. Mech.Engin., 2013, 49(4): 6-12.

[2] 王坤, 黄松龄, 赵伟. 平板兰姆波与缺陷作用边界元仿真实现研究[J]. 中国机械工程, 2009, 20(8): 887-891.WANG Kun, HUANG Songling, ZHAO Wei. Study on implementation of boundary element method simulation for Lamb wave interaction with defects in elastic plate[J]. China Mechanical Engineering, 2009, 20(8): 887-891.

[3] WANG X, YING C F. Scattering of Lamb waves by a circular cylinder[J]. J. Acoust. Soc. Am., 2001, 110(4): 1752-1763.

[4] Castaings M, Clezio E L, Hosten B. Modal decomposition method for modeling the interaction of Lamb waves with cracks[J]. J.Acoust. Soc. Am., 2002, 112(6): 2567-2582.

[5] Dilligent O, Grahn T A, Boström A, et al. The low-frequency reflection and scattering of the S0Lamb mode from a circular through-thickness hole in a plate: Finite Element, analytical and experimental studies[J]. J. Acoust. Soc. Am., 2002, 112(6):2589-2601.

[6] Grahn T. Lamb wave scattering from a circular partly through-thickness hole in a plate[J]. Wave Motion, 2003, 37: 63-80.

[7] 邓庆田, 杨智春. 导波在多损伤结构中的散射[J]. 振动与冲击,2010, 29(4): 40-43.DENG Qingtian, YANG Zhichun. Scattering of guided waves in a plate with multiple damages[J]. Journal of Vibration and Shock,2010, 29(4): 40-43.

[8] Moreau L, Caleap M, Velichko A, Wilcox P D. Scattering of guided waves by flat-bottomed cavities with irregular shapes[J].Wave Motion, 2012, 49: 375-387.

[9] Doyle J F. Wave propagation in structures[M]. Second Edition,New York: Springer, , 1997.

[10] Wang C H, Rose L R F. Wave reflection and transmission in beams containing delamination and inhomogeneity[J]. J. Sound. Vib.,2003, 264: 851-872

[11] Wang C H, Chang F K. Scattering of plate waves by a cylindrical inhomogeneity[J]. J. Sound. Vib., 2005, 282: 429-451.

[12] Kane T R, Mindlin R D. High-frequency extensional vibrations of plates[J]. J. Appl. Mech., 1956, 23: 277-283.

[13] Mindlin R D. Influence of rotary inertial and shear on flexural motions of isotropic, elastic paltes[J]. J. Appl. Mech., 1951, 18:31-38

[14] Wang C H, Rose L R F. Wave reflection and transmission in beams containing delamination and inhomogeneity[J]. J. Sound. Vib.,2003, 264: 851-872.

[15] Mckeon J C P, Hinders M K. Lamb wave scattering from a through hole[J]. J. Sound. Vib., 1999, 224(5): 843-862.