一种应变式超低频微振动测试台

陈江攀，程 伟，夏明一

（北京航空航天大学航空科学与工程学院，北京 100191）

一种应变式超低频微振动测试台

陈江攀，程 伟，夏明一

（北京航空航天大学航空科学与工程学院，北京 100191）

为了测试卫星太阳翼驱动机构低频、超低频区由机电耦合产生的微振动，发明了一种应变式超低频微振动六分量测试台，该测试台低频响应特性好，安装接口灵活。介绍该测试台的工作原理和动态标定方法，并对该测试台进行了线性度检验、固有频率测试以及动态测试误差检验。通过线性度检验可得：在100 N范围内的外力作用下，组成该测试台的八个双孔梁应变式力传感器的线性度相对误差在±3.4%以内；通过固有频率测试可得：该测试台在100 Hz内没有固有频率，不会通过结构耦合对被测微振动信号进行调制；通过动态测试误差检验可得：在频域上0～100 Hz范围内，该测试台对六个分量动态测试的相对误差在±9.6%以内，同时还可以得出该测试台对三个力分量和三个力矩分量的测试分辨率分别可达到0.01 N和0.001 N·m。

超低频；微振动；六分量；动态标定

卫星太阳翼驱动机构低频、超低频区由机电耦合产生的微振动会对卫星的成像质量和指向精度等关键性能产生较大影响［1］，因此通过测试来研究太阳翼驱动机构低频、超低频区微振动的特性是十分必要的。传统的压电式微振动六分量测试台低频响应特性差［2－3］，瑞士KISTLER公司生产的压电式微振动六分量测试台虽然解决了压电式力传感器低频响应特性差的缺点，但是其安装接口不够灵活，这都导致目前对太阳翼驱动机构低频、超低频区微振动的测试尚未实现。本文发明了一种应变式超低频微振动六分量测试台，应变式力传感器低频响应特性好，可以实现静态（0 Hz）测试，克服了压电式力传感器低频响应特性差的缺点；该测试台内部是一个空腔，被测扰动源既可以安装在测试台内部也可以安装在测试台外部，克服了KISTLER公司生产的六分量测试台安装接口不够灵活的缺点，因此该测试台可以实现对太阳翼驱动机构低频、超低频区微振动的测试。该测试台主要由八个双孔梁应变式力传感器和负载盘组成，利用双孔梁受弯矩作用时特殊的应变效果［4］，通过对应变片合理的布局以及测试电路合理的设计即可同时测得空间正交的三个力（Fx、Fy和Fz）和三个力矩（Mx、My和Mz），即六分量。

本文首先介绍了六分量测试台的工作原理和动态标定方法，然后对其进行了线性度检验、固有频率测试以及动态测试误差检验。结果表明：六分量测试台的线性度和稳定性好，低频区不会对被测信号进行调制，动态测试误差小，测试分辨率高。本文的发明为卫星活动部件低频、超低频区微振动的测试和研究提供了有力的帮助。

1 测试台工作原理

六分量测试台主要由八个双孔梁应变式力传感器和负载盘组成，其实物照片参见图1，其内部示意图参见图2。

图1 六分量测试台实物图Fig.1 Picture of the testing platform

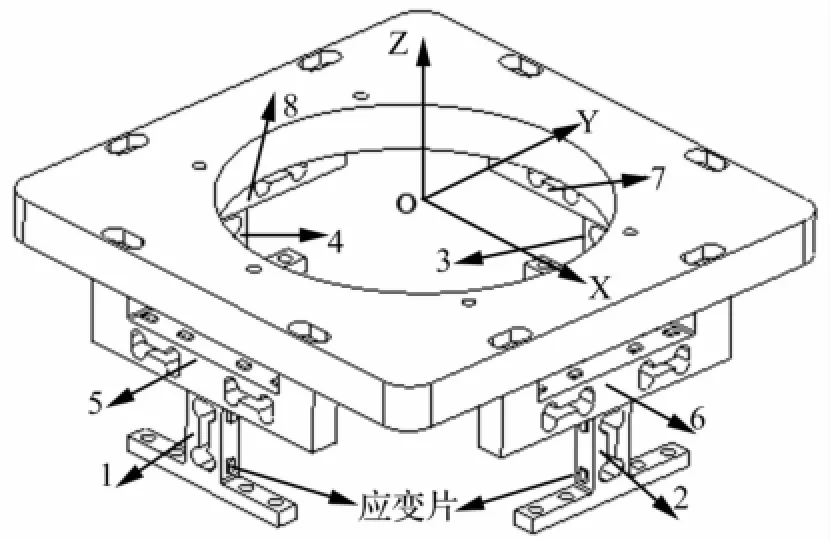
图2 六分量测试台内部示意图Fig.2 Internal schematic of the testing platform

双孔梁应变式力传感器具有结构刚度高、稳定度好、灵敏度高以及滞后小等优点，广泛应用于称重领域［5－6］。常用双孔梁应变式力传感器的结构如图2中竖直双孔梁力传感器1所示，即在板状梁上有两个孔，当在梁的端部有集中力作用时，孔内承受弯曲变形，将应变片粘贴在孔的外壁或内壁，应变片处于相反的应力区内，即孔壁上粘贴的四片应变片刚好有两个处于正应力区，两个处于负应力区，四个应变片恰好组成了一个等臂对称全桥测量电路［7］。为了结构对称，水平双孔梁力传感器5～8均由两个双孔梁组成，而竖直双孔梁力传感器1～4均为一个双孔梁，如图2所示。

应变片的粘贴位置参见图3，其中竖直双孔梁力传感器1～4在4个半圆孔对应的平面上粘贴应变片，即应变片a～d；水平双孔梁力传感器5～8只在靠近负载盘的四个半圆孔对应的平面上粘贴应变片，即应变片e～h。应变片的组合方式为：每个双孔梁力传感器上的四片应变片组成一个等臂对称全桥电路，其中应变片a和c接入相对桥臂，应变片b和d接入该全桥电路的另一对相对桥臂；应变片e和g接入相对桥臂，应变片f和h接入该全桥电路另一对相对桥臂。双孔梁力传感器1～4负责测试Fx、Fy和Mz三个分量，双孔梁力传感器5～8负责测试Fz、Mx和My三个分量。通过对应变片合理的布局以及测量电路合理的设计即可实现对六分量同时进行动态测试。

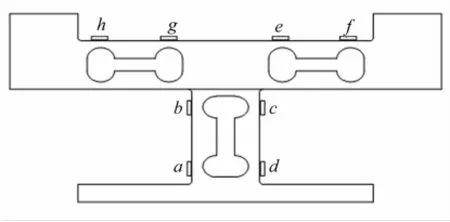
图3 应变片粘贴位置示意图Fig.3 Schematic of the location pasting strain gauge

2 动态标定方法

六分量测试台的动态标定是在频域内完成的。由于六分量测试台在进行动态测试时输出的是电压信号，即响应信号，为了能从测试到的响应信号U（ω）中确定出激励信号F（ω），首先应该求得相应的标定矩阵W（ω）。整体的标定矩阵实际上是八个双孔梁力传感器的响应信号与作用在等效中心点的载荷之间的频响函数矩阵。对于本文发明的六分量测试台，等效中心为负载盘上表面的几何中心点O，在此中心点直接施加六个分量难以实现，本文在假设负载盘为刚体的基础上，安装一个刚度很高的标定装置，并选择如图4所示的16个加载点，通过力锤敲击对其进行加载。根据空间力系平衡理论可知，利用选择的16个加载点能等效出作用在负载盘几何中心点的六个分量。图4给出了标定装置的示意图，其中O点为负载盘上表面的几何中心点，Lx、Ly和Lz分别为加载点对O点的力臂。

标定过程中，利用力锤敲击对标定装置施加F1至F1616个力，通过数据采集系统可测得八个双孔梁力传感器与每个敲击力的频响函数，以此来计算系统的标定矩阵W（ω）。由文献［8］可知，系统的响应与激励之间的关系为：

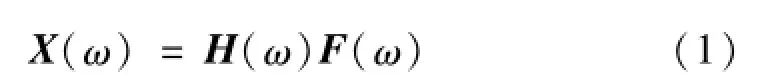
其中：X（ω）为系统的响应，F（ω）为系统的激励，H（ω）为频响函数。在六分量测试台动态标定过程中，系统的响应为八个双孔梁力传感器的输出电压，激励为16个敲击力，则式（1）可写为：

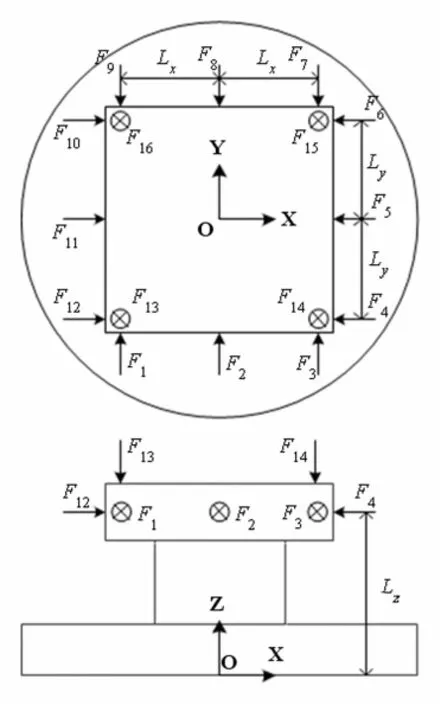
图4 标定装置示意图Fig.4 Schematic of the calibration device

八个传感器的输出电压与等效载荷之间的关系可写为：

3 线性度检验

对负载盘几何中心点分别施加沿X轴、Y轴和Z轴方向10 N、20 N、50 N和100 N四种不同重量的砝码来检验八个双孔梁力传感器的线性度。当沿X轴方向施加砝码时，检验传感器1和3的线性度；当沿Y轴方向施加砝码时，检验传感器2和4的线性度；当沿Z轴方向施加砝码时，检验传感器5～8的线性度。线性度检验实验中，采样时间为32 s，采样频率为8 Hz。由于六分量测试台是一个对称机构，本文只选取传感器1、2和5的线性度检验结果进行展示，参见图5。

由图5可知，双孔梁力传感器1、2和5的线性度和稳定性良好。表1给出了八个双孔梁力传感器输出电压的均值与施加砝码重量的比值。由表1可知，八个双孔梁力传感器的线性度良好。以10 N砝码作用时输出电压的均值与砝码重量比值为基准计算线性度相对误差，其计算公式为：

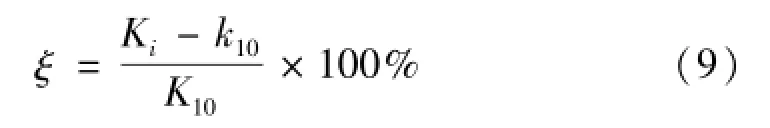
表1 输出电压与砝码重量比值Tab.1 Ratio of output voltage and load weight

其中：K10为10 N砝码作用时输出电压的均值与施加砝码重量的比值，Ki（i＝20，50，100）为其它三种重量砝码作用时输出电压的均值与施加砝码重量的比值。线性度相对误差计算结果参见表2。

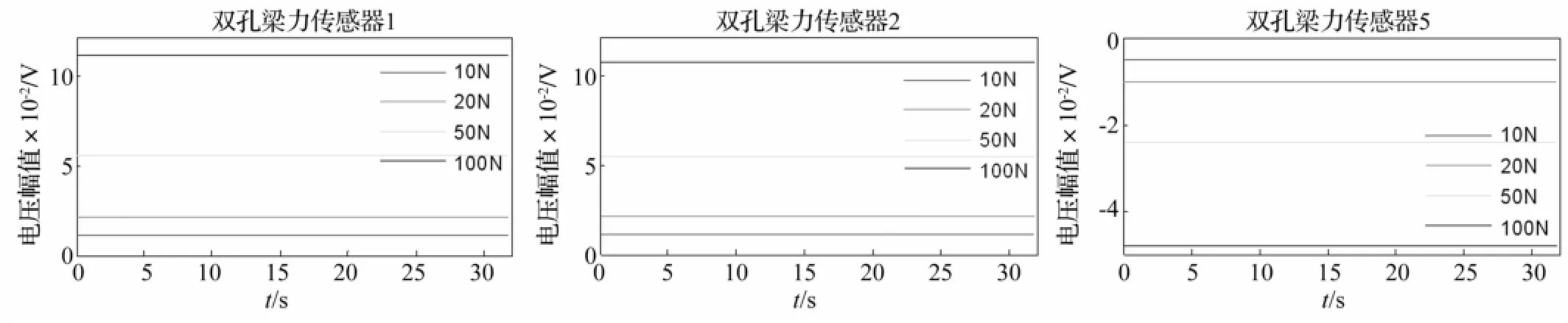
图5 线性度检验结果Fig.5 Result of linearity examination

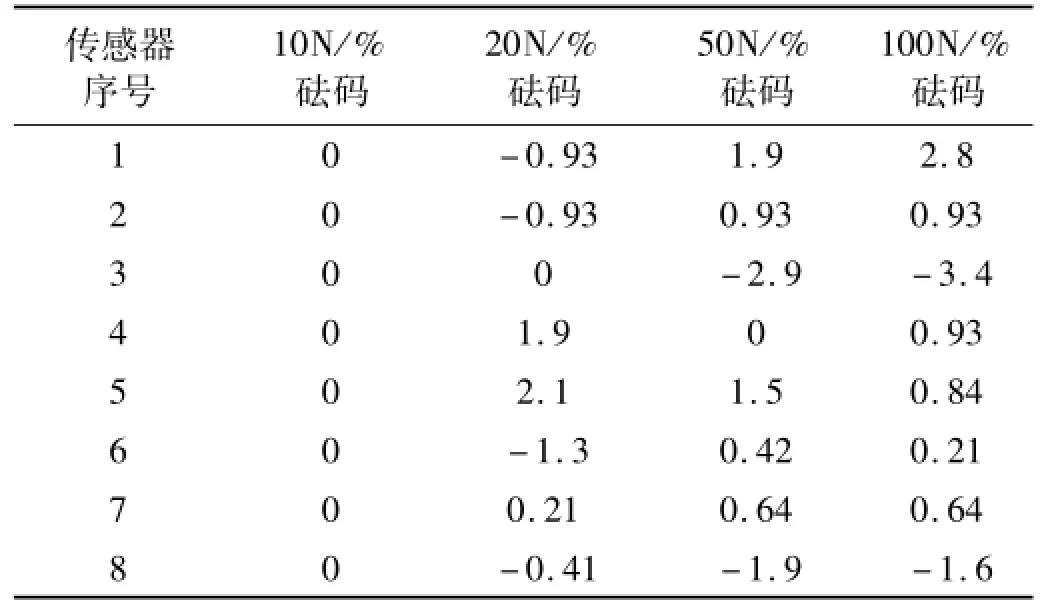
表2 线性度相对误差计算结果Tab.2 Result of linearity relative error

由表2可知，在100 N范围内的外力作用下，八个双孔梁力传感器的线性度相对误差在±3.4%以内。

4 固有频率测试

通过力锤敲击对六分量测试台的标定装置施加一个脉冲激励，然后分析八个双孔梁力传感器的频域响应特性，从而得到六分量测试台的固有频率。图6给出了脉冲激励下双孔梁力传感器1的频域响应曲线。

由图6可知，六分量测试台在100 Hz内没有固有频率，在进行动态测试时不会通过结构耦合对被测微振动信号调制，使其低频、超低频区域的测试结果有效。

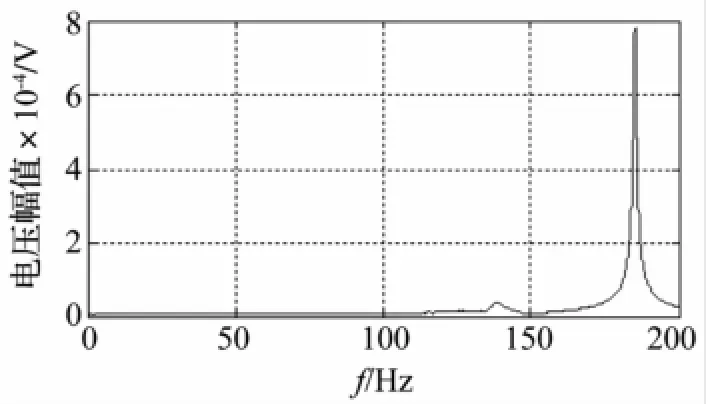
图6 传感器1的频域响应曲线Fig.6 Response of sensor No.1 in frequency domain

5 动态测试误差检验

通过对标定装置的16个加载点进行敲击，来获得六分量测试台的动态标定矩阵，标定过程中数据采集系统的采样频率为2 048 Hz，采样时间为16 s。为了检验六分量测试台的动态测试误差，在获得其动态标定矩阵后，再次用力锤敲击标定装置的加载点进行误差检验。由式（3）可知，敲击加载点1的等效载荷为Fy、Mx和Mz，敲击加载点5的等效载荷为Fx、My，敲击加载点16的等效载荷为Fz、Mx和My，因此通过再次敲击加载点1、5和16并比较实际值与测试结果即可获得六个分量的动态测试误差。

通过数据采集系统采集三次敲击的敲击力F（ω）以及相应的测试台输出电压U（ω）。将采集到的敲击力F（ω）右乘其对应的转化矩阵Ci即可得到其等效载荷F′（ω）；将采集到的输出电压U（ω）右乘已获得的标定矩阵W（ω）即可获得六分量测试台的测试结果F″（ω），即

动态测试的相对误差计算公式为：

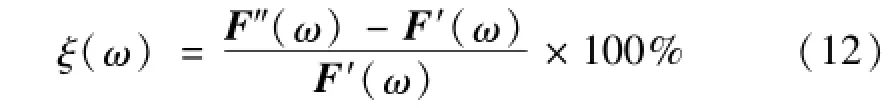
利用加载点1处的Fy、Mx和Mz分量，加载点5处的Fx、My分量以及加载点16处的Fz分量进行误差检验。图7给出了0～100 Hz范围内六个分量的实际值和测试结果的对比图。表3给出了由式（12）计算得到的0～100 Hz内六个分量动态测试的最大相对误差。

表3 六个分量100 Hz内动态测试的最大相对误差Tab.3 Maximum relative error of dynamic testing

由图7可以看出，在频域上100 Hz内六分量测试台对三个力分量的测试分辨率可达到0.01 N，对三个力矩分量的测试分辨率可达到0.001 Nm。由表3可以得出，在频域上100 Hz内测试台对六个分量动态测试的相对误差在±9.6%以内。同时发现Fz、Mx和My三个分量的相对误差较大，这是由于激励载荷不够大使得测试台的输出电压过小，背景噪声对测试精度的影响开始显著。

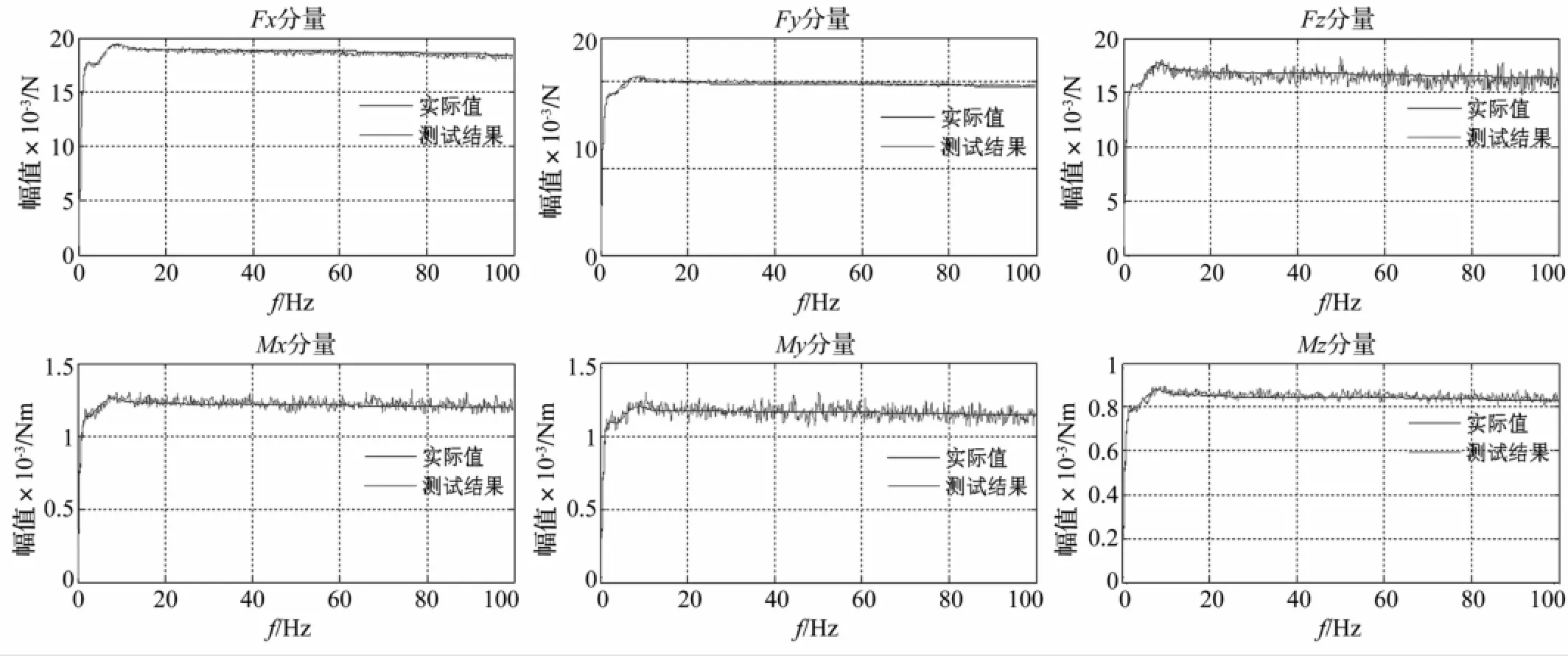
图7 实际值与测试结果对比图Fig.7 Contrast figure of actual value and testing result

6 结 论

本文发明了一种应变式超低频微振动六分量测试台，并详细介绍了其工作原理和动态标定方法。通过对六分量测试台进行线性度检验、固有频率测试以及动态测试误差检验可以发现，该测试台的八个双孔梁应变式力传感器线性度和稳定性良好，低频、超低频区不存在结构耦合对被测信号的调制，动态测试的相对误差小、分辨率高。本文的发明为卫星活动部件低频、超低频区微振动的测试和研究提供了有力的帮助。然而在进行动态测试误差检验时还发现，当激励载荷过小时，背景噪声的影响比较显著，使得测试误差偏大，因此六分量测试台的灵敏度有待进一步提高，以满足更小量级微振动的精确测试。

［1］张鹏飞，程伟，赵煜.考虑耦合效应的动量轮扰动测量［J］.北京航空航天大学学报，2011，37（8）：948－952.

ZHANG Peng-fei，CHENG Wei，ZHAO Yu.Measure of reaction wheels disturbance considering coup ling effect［J］.Journal of Beijing University of Aeronautics and Astronautics，2011，37（8）：948－952.

［2］刘向阳，张平，韩振海.动态补偿法在压电传感器静态校准中的应用［J］.仪器仪表学报，2004，25（4）：9－10.

LIU Xiang-yang，ZHANG Ping，HAN Zhen-hai.Application of dynamic compensation method to static calibration of piezoelectric sensors［J］.Chinese Journal of Scientific Instrument，2004，25（4）：9－10.

［3］鲁捷，孟凡文，张玉香.改进压电传感器频率响应特性的措施［J］.中国仪器仪表，2006，11：79－81.

LU Jie，MENG Fan-wen，ZHANG Yu-xiang.The discuss on improving frequency response properties of piezoelectricity sensor［J］.China Instrumentation，2006，11：79－81.

［4］潘雪涛，温秀兰.传感器原理与检测技术［M］.北京：国防工业出版社，2011：33－51.

［5］何芝仙，常小强，李震.双孔平行梁式传感器设计的理论分析与实验研究［J］.试验技术与试验机，2006，46（1）：14－17.

HE Zhi-xian，CHANG Xiao-qiang，LI Zhen.Theoretical analysis and experimental research on the beam sensorwith two parallel holes［J］.Test Technology and the Testing Machine，2006，46（1）：14－17.

［6］谢永华，孟凡虎.双孔平行梁式称重传感器非线性校正研究［J］.现代科学仪器，2010（6）：64－66.

XIE Yong-hua，MENG Fan-hu.Nonlinear correction study of double parallel beam weighing transducer［J］.Modern Scientific Instruments，2010（6）：64－66.

［7］王琦.电阻应变式称重传感器的设计［J］.木材加工机械，2005，3：20－23.

WANG Qi.Design of the weighing-sensor of resistance-strain model for measuring wood moisture content［J］.Wood Processing Machinery，2005，3：20－23.

［8］邢誉峰，李敏.工程振动基础［M］.2版.北京：北京航空航天大学出版社，2011：36－37.

An ultra-low frequency m icro-vibration testing p latform based on strain-resistance effect

CHEN Jiang-pan，CHENGWei，XIAMing-yi
（School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

In order to measure micro-vibration of a SADA（solar array drive assembly）in low and ultra-low frequency zone caused by electromechanical coupling，a six-component testing platform based on strain-resistance effect was developed.Its response characteristic in low frequency zonewas outstanding and its installation interfacewas flexible.The working principle and dynamic calibration method of this platform were introduced in detail.In order to assess the performance of this testing platform，linearity examination，natural frequencies measurement and dynamic testing error examination for itwere done.The results showed that linearity errors of eight force sensors are within 3.4%under the action of external forcewithin 100N；there are no natural frequencieswithin 100Hz，so that themicro-vibration signals can not be modulated through structural coupling in frequency domain of（0－100Hz）；dynamic testing errors of six components are within±9.6%in frequency domain of（0－100Hz），testing resolutions of three forces and three moments can reach 0.0lN and 0.001N.m，respectively.

ultra-low frequency；micro-vibration；six-component；dynamic calibration

TH823；TH825

A

10.13465/j.cnki.jvs.2014.24.013

2013－09－23 修改稿收到日期：2014－01－02

陈江攀男，博士生，1988年4月

程伟男，教授，1961年11月