基于Timoshenko梁理论的微细立铣刀动力学建模
2014-05-16方泽平王西彬刘志兵徐宗伟
方泽平,王西彬,刘志兵,陈 明,徐宗伟
(1.北京理工大学先进加工技术国防重点学科实验室,北京 100081;2.上海交通大学机械与动力工程学院,上海 200240;3.天津大学精密测量技术与仪器国家重点实验室,天津 300072)
基于Timoshenko梁理论的微细立铣刀动力学建模
方泽平1,王西彬1,刘志兵1,陈 明2,徐宗伟3
(1.北京理工大学先进加工技术国防重点学科实验室,北京 100081;2.上海交通大学机械与动力工程学院,上海 200240;3.天津大学精密测量技术与仪器国家重点实验室,天津 300072)
应用Timoshenko梁理论综合考虑了微细立铣刀特殊结构及其高转速工况引起的剪切效应和惯性效应,建立了微细立铣刀悬伸部分的动力学模型;分析了所建立的模型的收敛性问题,通过试验验证了模型的准确性,并与欧拉梁理论计算结果和有限元软件仿真结果比较,证明了模型的适用性;利用建立的微细立铣刀动力学模型,研究了微细立铣刀刀头直径、刀头部分长径比和刀颈半锥角等刀具结构参数对刀具固有频率的影响。模型可用于微细立铣刀的参数化设计和优化,改善其动力学特性。
微细立铣刀;动力学建模;Timoshenko梁;固有频率
微细铣削是采用直径极小的铣刀进行材料去除的一种加工方法[1]。为了获得足够的切削线速度和材料去除率,微细立铣刀的转速极高。通常,微细铣削的特征尺寸极小,要想获得足够的相对精度,需要达到极高的绝对精度,这对系统的动力学提出了极高的要求。考虑到刀具本身复杂的特性,微细立铣刀对微细铣削过程中的动态响应起重要作用。
目前只有少量文献研究了微细立铣刀的动力学模型。Filiz等[2-4]提出微细立铣刀包括粗短的结构和多种尺度范围,需要考虑一般被忽略的剪切效应,传统的Euler-Bemoulli梁并不适用。而且,在微细铣削过程中使用极高的转速,需要考虑动力学模型中的惯性效应。Jun等[5-6]通过将沟槽部分的横截面近似为圆形,采用Timoshenko横梁模型,研究了微细立铣刀的动态特性。Mustapha等[7]开发了一种基于离散结构单元的动力学混合分析模型,研究了刀具结构和加工参数对刀具动态性能的影响。
本文基于Timoshenko梁理论,用分段思路[8]建立微细立铣刀的动力学模型,研究了微细铣刀结构参数对刀具固有频率的影响,可用于指导微细铣刀的结构设计和工艺参数优化。
1 微细立铣刀结构动力学建模
1.1 基于Timoshenko梁的动力学建模
沿梁的轴线方向z取微段dz为隔离体,微段所受载荷如图1所示。θ表示仅有弯曲变形时挠曲线的斜率,γ为微段的剪切变形,有

由微段的受力平衡条件建立Timoshenko梁横向挠曲运动微分方程:

式中:A为截面面积;I为截面惯性矩;ρ为材料密度;E为材料弹性模型;G为材料剪切模量;k为截面的剪切变形系数。q为横向分布载荷,m为分布外力矩。

图1 Timoshenko梁微段的受力图Fig.1 Force diagrams of the infinitesimal element of Timoshenko beam
考虑自由振动状态,则q=0,m=0。
根据式(2),有
1.2 微细立铣刀的动力学建模
根据微细立铣刀的铣削加工形式,可以简化为如图2所示的不等截面Timoshenko悬臂梁模型。通常将铣刀分为三部分:刀柄部分为等截面圆柱梁,刀径部分为锥形梁,可简化为如图2所示的等梯度变化等截面阶梯梁,刀头部分同样简化为等截面圆柱梁。
因为微细立铣刀的截面尺寸与长度相比不算很小,且工作转速很高,转动惯量与剪切变形不可忽略,因此采用Timoshenko横梁方程描述其动态特性,以综合考虑剪切变形和转动惯量效应的影响。

图2 微细立铣刀的简化模型Fig.2 Model of micro-endmill
基于分段思想,将微细立铣刀分为互相连接的若干段,如图2所示。第i段梁长度、截面面积和截面惯性矩可分别表示为:
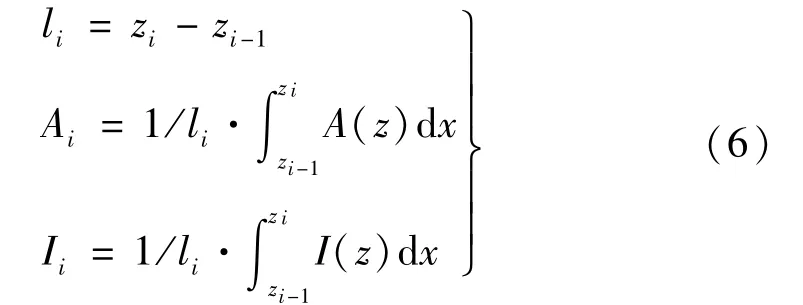
因此,第i段梁的模态函数为:

考虑i=1,2,…,N-1,得第1段待定系数C(1)和第N段待定系数C(N)之间的关系:

微细立铣刀安装后为悬臂梁结构,其边界条件:

将式(7)代入相应的边界条件,建立包含C1~C4的四个齐次方程。因为齐次方程存在非零解,可通过方程的特征方程式计算固有频率,进而求解相应振型。
2 模型精度分析
为了确定分段数对计算精度的影响,即收敛性,对比分析了不同分段数所得的固有频率,并利用有限元仿真结果进行评估。第r阶固有频率因分段数增加导致的偏差可以表示为:

选取表1所列的微细立铣刀结构参数,刀具材料密度ρ=14.45×103kg/m3,杨氏模量E=580 GPa,剪切模量G=242 GPa,截面剪切系数k=0.9,则其前三阶的固有频率的收敛性如图3所示。由图可见,分段数n=224时,获得的微细立铣刀前三阶模态的偏差已低于0.04%。

表1 微细立铣刀结构参数Tab.1 Structure parameters of micro-endmill
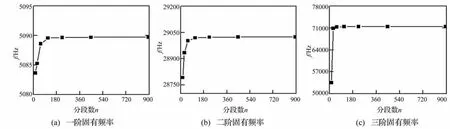
图3 模型的收敛性Fig.3 Convergence behavior for the model

图4 实验装置Fig.4 Experimental setup

图5 一阶固有频率实验值Fig.5 Experimental result of the first natural frequency
为了验证所建立模型的正确性,将微细立铣刀安装在微小型数控车铣磨复合加工中心CXKM25-Ⅲ上,如图4所示,采用Polytec激光测振仪CLV2534-2测量铣刀上节点在振动冲击力锤敲击下的响应信号。力锤和测振仪采集的信号经电荷电压滤波积分放大器DLF-6和智能信号采集处理分析仪INV306DF5120传输到计算机进行数据处理。取三次有效敲击(每次锤击的相干系数均大于0.85)的平均为最终结果。实验结果如图5所示,测得的一阶固有频率为4 846.87Hz,与计算的理论值的相对误差为5.02%。
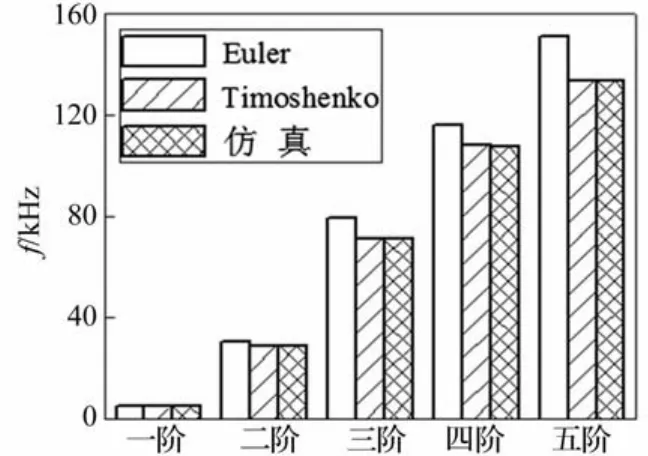
图6 固有频率计算结果Fig.6 Calculated results of natural frequency
为了比较高阶频率时,不同模型对计算结果的影响,以ABAQUS有限元软件进行铣刀实体模型仿真的结果为基准,将Euler梁模型、Timoshenko梁模型计算获得的固有频率值与ABAQUS有限元仿真的结果进行比较,如图6所示。可见,对于微细铣刀结构,采用Timoshenko梁方法获得的结果更为准确,而且频率越高,效果越明显。采用224个分段数的计算结果与ABAQUS仿真软件铣刀实体模型的动态仿真结果的误差范围控制可在1%以内。可见,该算法具有较高的计算精度,适用于对微细立铣刀结构的动力学分析。
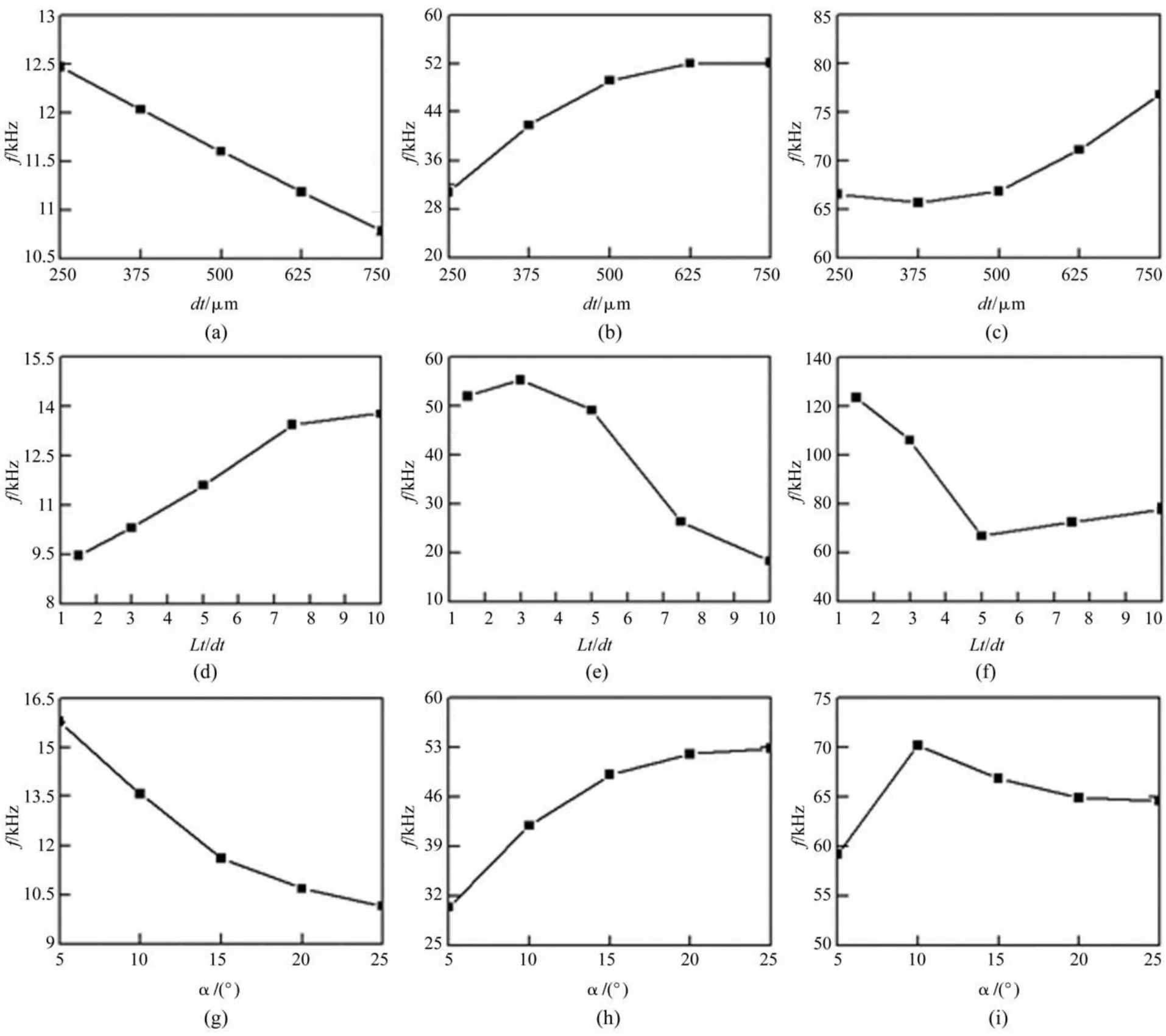
图7 固有频率随刀具结构参数的变化Fig.7 Natural frequency with the variation of tool structure parameters
3 刀具结构参数对动力学特性的影响规律
基于所建立的微细立铣刀动力学模型,分析了微细立铣刀几何结构对微细立铣刀固有频率的影响。分析的参数包括刀头部分直径dt(从250 μm到750μm)、刀头部分长径比Lt/dt(1.5~10)、半锥角α(5°~30°)。刀柄直径ds和悬伸长度L保持不变,分别为3 mm和20 mm。安装误差和主轴速度设置为0。
图7(a)~(c)显示了刀头直径对前三阶固有频率的影响。当分析刀头直径影响时,刀头长度、刀锥角分别为2.5 mm和15°。从图中可以看出在一阶模态,固有频率随刀头直径的增大而减小;在二阶模态,固有频率却随刀头直径的增大而增大,并趋于平稳;在三阶模态,刀头直径从250 μm增大到375 μm时,固有频率略微减小,而后随着直径的增大急剧增大。
图7(d)~(f)显示了刀头直径500 μm,半锥角15°时,刀头部分长径比对固有频率的影响。随着长径比的增大,刀具的一阶固有频率增大,二阶固有频率减小。当长径比从1.5增大到5时,三阶固有频率减小,而后随着长径比的继续增大开始逐渐变大。
图7(g)~(i)显示了刀头直径500 μm,刀头长径比5时,微细立铣刀半锥角对刀具固有频率的影响。随着刀具半锥角的增大,刀具一阶和二阶固有频率的变化趋势完全相反,三阶固有频率在半锥角为10°时最大,随后减小并趋于平稳。
三个刀具结构参数按对刀具固有频率影响的剧烈程度由大到小依次为刀头部分长径比、刀颈半锥角和刀头直径。各刀具结构参数对各阶频率的影响趋势也各不相同。通过合理的刀具结构参数设计,可以有效调整刀具的动态特性,获得满足应用需求的微细刀具。
4 结 论
(1)根据Timoshenko梁模型,应用分段思想建立了微细立铣刀悬伸部分的动力学模型,综合考虑了微细立铣刀结构和高转速工况引起的不可忽略的剪切效应和惯性效应,改进了微细立铣刀固有频率的求解方法。
(2)分析了模型分段数对模型计算精度的影响,通过模态实验测量微细铣刀安装状态下的固有频率,验证了模型的准确性,并将所建模型求得的固有频率与有限元软件仿真结果和Euler梁理论的计算结果进行对比,证明了所建模型求解微细立铣刀动力学问题的适用性。
(3)利用建立的微细立铣刀动力学模型,分析了微细立铣刀刀头直径、刀头部分长径比和刀颈半锥角对刀具固有频率的影响。模型的精度和适用性使其可用于基于动力学特性的微细立铣刀的设计研究和参数优化。
[1]Chae J,Park S.S,Freiheit T.Investigation of micro-cutting operations[J].International Journal of Machine Tools& Manufacture,2006,46:313-332.
[2]Filiz S,Ozdoganlar O B.Microendmill dynamics including the actual fluted geometry and setup errors-PartⅠ:Model development and numerical solution[J].Transactions of the ASME,2008,130.
[3]Filiz S,Ozdoganlar O B.Microendmill dynamics including the actual fluted geometry and setup errors-PartⅡ:Model validation and application[J].Transactions of the ASME,2008,130.
[4]Filiz S,Ozdoganlar O B.A three-dimensional model for the dynamics of micro-endmills including bending,torsional and axial vibrations[J].Precision Engineering,2011,35:24 -37.
[5]Jun M B G,Liu X,Devor R E,et al.Investigation of the dynamics of microend milling-PartⅠ:Model development [J].ASME J.Manuf.Sci.Eng.,2006,128:893-900.
[6]Jun M B G,Liu X,Devor R E,et al.Investigation of the dynamics of microend milling-PartⅡ:Model validation and interpretation[J].ASME J.Manuf.Sci.Eng.,2006,128:901-912.
[7]Mustapha K B,Zhong Z W.A hybrid analytical model for the transverse vibrationresponseofamicro-endmill[J].Mechanical Systems and Signal Processing,2013,34:321 -339.
[8]崔灿,蒋晗,李映辉.变截面梁横向振动特性半解析法[J].振动与冲击,2012,31(14):85-88.
CUI Can,JIANG Han,LI Ying-hui.Semi-analytical method for calculating vibration characteristics of variable cross-section beam[J].Journal of Vibration and Shock,2012,31(14):85 -88.
Dynamic modeling of a micro-endmill based on Timoshenko beam theory
FANG Ze-ping1,WANG Xi-bin1,LIU Zhi-bing1,CHEN Ming2,XU Zong-wei3
(1.Key Laboratory of Fundamental Science for Advanced Machining,Beijing Institute of Technology,Beijing 100081,China;2.School of Mechanical Engineering,Shanghai Jiaotong University,Shanghai 200240,China;3.State Key Laboratory of Precision Measuring Technology&Instruments,Tianjin University,Tianjin 300072,China)
A dynamic model for the over-hanged part of a micro-endmill was proposed comprehensively considering shear deformations and rotary inertia effect due to the nature of the micro-endmill with the theory of Timoshenko beam.The convergence behavior of the built model was analysed,and its correctness was verified with tests.The applicability of the model was proved by comparing the test data with the calculated results using the finite element method and the Euler beam theory.Based on the developed model,the effects of its tool tip diameter,tip section aspect ratio and semi-taper angle on the natural frequencies of the micro-endmill were studied.The proposed model provided a better basis for parametric design and optimization of micro-endmills to improve their dynamic performance.
micro-endmill;dynamic modeling;timoshenko beam;natural frequency
TH165;TG506.1
A
10.13465/j.cnki.jvs.2014.23.020
国家自然科学基金重点资助项目(50935001,51005023)
2013-06-07 修改稿收到日期:2013-12-19
方泽平男,博士生,1985年生
王西彬男,教授,博士生导师,1958年生
