P-碳的电学、力学性质的第一性原理预测
2014-05-15甄海龙刘红梅林巧文
甄海龙,高 海,刘红梅,林巧文
(山西大同大学物理与电子科学学院,山西大同037009)
由于碳可以具有多种成键方式,如sp、sp2和sp3杂化形式,能够形成众多具有优异的力学或电学特性的同素异形体结构。常见的如石墨、金刚石、碳纳米管(CNTs)、富勒烯(C60)、石墨烯(graphene)等。
层状石墨在高温高压的条件下(>15 GPa,>1 300 K),会发生sp2→sp3转变,生成立方或六方金刚石
[1]。实验发现,在冷压石墨过程中有结构异于金刚石的碳的同素异形体形成,并且硬度可与金刚石相比,但结构未知[2,3]。随后几个小组提出了几种模型来解释这种冷压石墨相[4-6]。2004年,Wang等人[7]在室温下压缩单壁碳纳米管束至75 GPa,在卸至常压的样品中观察到一种结构未知的新相存在。这些新奇的亚稳相的出现,是热力学和动力学共同作用的结果。探索高压下碳的亚稳相的结构演化、物理性质和形成机理,是材料学和物理学一个前沿的研究方向。
最近,Niu等人[8]提出一种名为P-碳的结构解释冷压碳纳米管束产生的未知相。这种P-碳可以看成是(2,2)或(4,4)纳米管束在静水压或非静水压作用下,通过相邻管束彼此相连而形成。理论模拟P-碳的X射线衍射图谱与Wang等人[7]实验中观察到的冷压碳纳米管相的X1射线衍射图谱吻合的很好。理论计算显示,P-碳的焓值在压力为9.4 GPa左右开始低于石墨相,表明在高压下P-碳是一种热力学比石墨更稳定的结构,有可能通过冷压石墨的方法获得。由于碳的同素异形体之间物理性质随结构的不同会有显著差异,本文采用第一性原理计算方法预测了这种P-碳的电学和力学性质,为将来新型功能材料的实验合成及应用提供理论参考。
1 计算方法
本文计算均采用Materials Studio软件中基于密度泛函理论的CASTEP模块进行[9]。采用超软赝势来描述电子-离子间相互作用[10],交换-关联泛函采用局域密度近似CA-PZ描述[11,12],平面波截止能设置为310 eV,C的价电子处理为2s22p2。布里渊区k点采样采用Monkhorst-Pack(MK)方案[13],k点选取为2π × 0.04。采用BFGS(Broyden-Fletcher-Goldfarb-Shanno)方法对结构进行优化[14]。结构优化的精度设置为:每个原子的能量变化小于5×10-6eV,施加到每个原子上的外力小于0.01 eV/,应力分量小于0.02 GPa,每个原子最大位移小于5.0×10-4。
2 结果与讨论
P-碳的空间群Pmmn(59),属正交晶系。每个晶胞中包含16个原子。原子间形成的均为扭曲四配位成键。在P-碳中C原子占据四个等价的Wyckoff坐标位置,分别为 4e(-1/2,0.185,0.292),4e(-1/2,0.182,-0.036),4e(-1/2,0.312,-0.541)和 4e(1/2,0.184,-0.215)。与金刚石中C原子全部六元环排列方式不同,P-碳中C原子形成的是四、六和八元环相互连接的复杂排列方式。碳纳米管沿径向的拉伸强度很高,但沿轴向很软。而通过冷压碳纳米管束使一维碳纳米管结构聚合成三维聚合物结构,同时碳纳米管中全sp2杂化方式转变为P-碳中sp3杂化方式。伴随结构和成键方式的改变,P-碳的力学性质也发生变化。表1中列出了金刚石和P-碳的晶参数,实验值也列出作为比较。理论计算的P-碳的体模量接近于金刚石,这暗示P-碳有可能是一种超硬材料。通常以体模量和剪切模量的比值B/G大小划分材料的脆性和韧性[15],临界值为1.75。当B/G的比值小于1.75时,是脆性材料,当B/G的比值大于1.75时,是韧性材料。计算的P-碳的B/G值为0.9,类似于金刚石,P-碳是一种脆性材料。

表1 金刚石和P-碳的参数表
图1为理论计算的P-碳的电子能带图,可以看出,P-碳为一种间接带隙半导体,价带顶位于Γ点,导带底位于Z-T方向。计算的间接带隙为3.47 eV,低于理论计算的金刚石的带隙值(4.2 eV)。这种宽带隙的特征表明P-碳是一种对可见光透过的材料,具有奇异的光学特性。
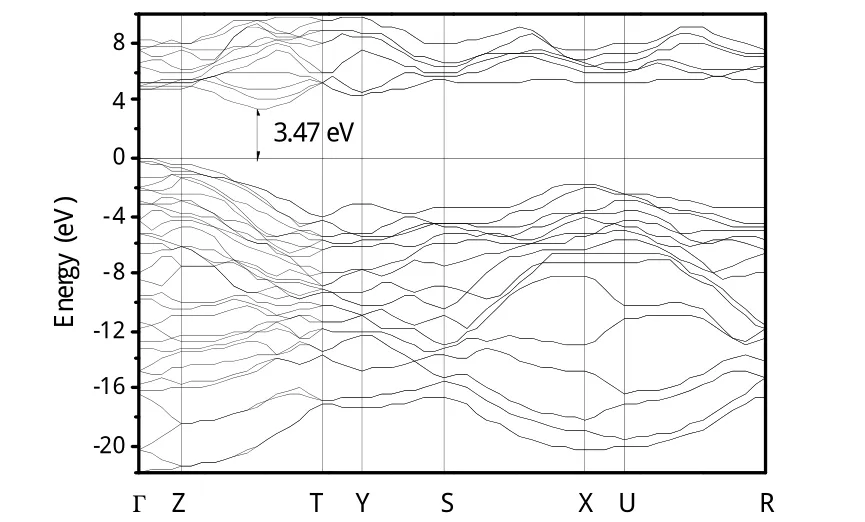
图1 P-碳的电子能带图
采用文献[18]中半经验的硬度计算的微观模型来计算金刚石和P-碳的维氏硬度。硬度可用下面公式计算:
Hv=350(Ne)e/d。
其中,Hv是维氏硬度(GPa),Ne为价电子密度,fi是Phillips定义的化学键的离子性,对于碳材料,fi取0,d为化学键键长。计算结果如表2所示。

表2 金刚石和P-碳的Vickers硬度理论计算值
通常定义维氏硬度超过40 GPa的材料为超硬材料。金刚石是已知硬度最高的材料,其维氏硬度高达96 GPa[19]。理论计算的金刚石的维氏硬度98.2 GPa,与实验值符合的很好。理论计算的P-碳的维氏硬度为96.3 GPa,略低于金刚石的硬度,表明P-碳是一种潜在的超硬材料,在工业上可作为磨削工具材料加以应用。
下面采用文献[20]中固体化学键的键强模型计算金刚石和P-碳的拉伸强度。晶体沿<hkl>方向的理想拉伸强度σhkl可表示为:

在这种模型中,i-j键的键强等于拆开i-j键所需的最大拉伸力Fij,而Fij只和i-j键的键长dij和i-j键上的有效成键价电子数nij有关。Shkl为沿(hkl)面每m2的化学键的面密度。
表3中列出了所计算的金刚石沿<111>方向和P-碳沿<010>方向的拉伸强度。可以看出,P-碳的拉伸强度接近于金刚石,表现出优异的力学性能。由于拉伸强度与键长成反比,与键的面密度成正比,因此键长越短、键的面密度越大的材料越具有较高的拉伸强度。
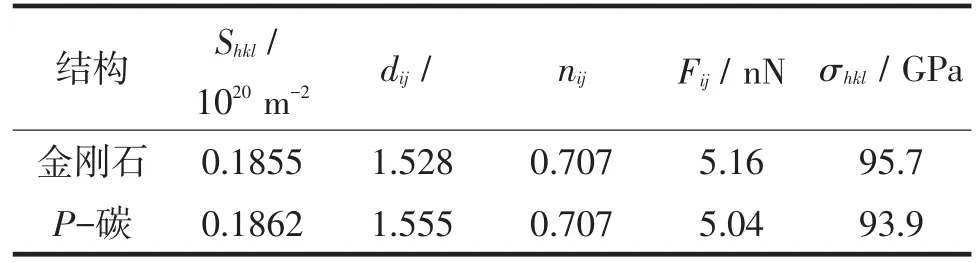
表3 金刚石和P-碳拉伸强度的理论计算值
3 结论
研究了一种碳的同素异形体P-碳的电学和力学性质。计算结果显示,这种P-碳是一种宽带隙半导体(3.47 eV),其硬度和拉伸强度接近于相应的金刚石的值。高压方法是一种有效的方法改变碳纳米管中原子的成键状态,产生丰富的3D碳纳米管聚合物,并且这些新奇的结构还有优异的电学或力学性能。获得的3D碳纳米管聚合物的结构与加压方式、晶格排列方式(如正交、四方、六方、立方等)、碳纳米管手性数(m,n)、管径d都有关系。探索压力下聚合碳纳米管束的结构和性质具有重大的理论和现实意义。
[1]Bundy F P,Bassett W A,Weathers M S,et al.The pressure-temperature phase and transformation diagram for carbon;updated through 1994[J].Carbon,1996,34(2):141-153.
[2]Miller E D,Nesting D C,Badding V.Quenchable transparent phase of carbon[J].Chem Mater,1997,9(1):18-22.
[3]Mao W L,Mao H K,Eng P J,et al.Bonding changes in compressed superhard graphite[J].Science,2003,302(5644):425-427.
[4]Li Q,Ma Y,Oganov A R,et al.Superhard monoclinic polymorph of carbon[J].Phys Rev Lett,2009,102(17):175506(1-4).
[5]Wang J T,Chen C,Kawazoe Y.Low-temperature phase transformation from graphite to sp3 orthorhombic carbon[J].Phys Rev Lett,2011,106(7):075501(1-4).
[6]Zhao Z S,Xu B,Zhou X F,et al.Novel Superhard Carbon:C-Centered Orthor hombicC8[J].Phys Rev Lett,2011,107(21):215502(1-5).
[7]Wang Z W,Zhao Y,Tait K,et al.A quenchable superhard carbon phase synthesized by cold compression of carbon nanotubes[J].Proc Natl Acad Sci U.S.A.2004,101(38):13699-13702.
[8]Niu H Y,Chen X Q,Wang S B,et al.Families of Superhard Crystalline Carbon Allotropes Constructed via Cold Compression of Graphite and Nanotubes[J].Phys Rev Lett,2012,108(13):135501(1-5).
[9]Segall M D,Lindan P J D,Probert M J,et al.First-principles simulation:ideas,illustrations and the CASTEP code[J].J Phys:Condens Matter,2002,14(11):2717-2720.
[10]Vanderbilt D.Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J].Phys Rev B,1990,41(11):7892-7895.
[11]Ceperley D M,Alder B J.Ground State of the Electron Gas by a Stochastic Method[J].Phys Rev Lett,1980,45(7):566-569.
[12]Perdew J P,Zunger A.Self-interaction correction to density-functional approximations for many-electron systems[J].Phys Rev B,1981,23(10):5048-5079.
[13]Monkhorst H J,Pack J D.Special points for Brillouin-zone integrations[J].Phys Rev B,1976,13(12):5188-5192.
[14]Pfrommer B G,Cté M,Louie S G,et al.Relaxation of Crystals with the Quasi-Newton Method[J].J Comput Phys,1997,131(1):233-240.
[15]Pugh S F.XCII.Relations between the elastic moduli and the plastic properties of polycrystalline pure metals[J].Philos Mag,1954,45(367):823-843.
[16]Yamanaka T,Morimoto S.Influence of the isotope ratio on the lattice constant of diamond[J].Phys Rev B,1994,49(14):9341-9343.
[17]Grimsditch M H,Ramdas A K.Brillouin scattering in diamond[J].Phys Rev B,1975,11(8):3139-3148.
[18]Gao F M,He J L,Wu E D,et al.Hardness of covalent crystals[J].Phys Rev Lett,2003,91(1):015502(1-4).
[19]Andrievski R A.Superhard materials based on nanostructured high-melting point compounds:achievements and perspectives[J].Int J Refract Met Hard Mater,2001,19(4):447-452.
[20]Guo X J,Wang L M,Xu B,et al.Unbinding force of chemical bonds and tensile strength in strong crystals[J].J Phys:Condens Matter,2009,21(48):485405(1-5).
