基于改进杂草优化算法的最优线性协作频谱感知

解武，李笑，李然

1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001 2.莫纳什大学信息技术学院，澳大利亚墨尔本 3145

基于改进杂草优化算法的最优线性协作频谱感知

解武1，李笑1，李然2

1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001 2.莫纳什大学信息技术学院，澳大利亚墨尔本 3145

线性加权协作频谱感知模型下，针对虚警概率最大化检测概率的问题，提出了一种基于改进入侵性杂草优化算法的协作频谱感知方案。算法中的可行解与频谱协作感知模型中的权重向量相对应，通过寻求最优权重向量，来达到最大化检测概率的目的。同时将改进后的杂草算法与传统的杂草算法及基于修正偏差因子方法性能进行对比。结果表明，改进后的杂草算法可根据当前噪声环境合理分配系统的权重系数，以较小的迭代次数找到更优的权重向量，在虚警概率一定的前提下，获得高的检测概率，其性能优于原始MDC算法。

认知无线电；频谱感知；最优线性协作；能量检测；杂草优化算法

随着无线业务的快速增长，无线电频谱的需求日益增加。然而，频谱资源有限，并且大多数已经分配给相应的授权用户在有限的频带内工作。为了处理频谱之间的不平衡和频谱利用率不足，认知无线电技术（cognitive radio，CR）被提出［1-3］以缓解无线频谱资源短缺及频谱利用率低下等问题。

频谱感知技术是认知无线电的关键技术，根据认知用户数分为单用户频谱感知和多用户合作频谱感知［4-5］。单用户频谱感知方法主要有匹配滤波器检测、能量检测和循环平稳特征检测［6］。但当受到阴影和多径影响时，存在的隐藏终端问题是实现频谱感知的巨大隐患，其使得单个认知用户不能准确确定未被占用的频段。而多点协作频谱感知是解决上述问题的有效方法之一［6-8］。文献［9］采用OR和AND准则，对各个感知结果进行融合，提高了检测的可靠性。文献［10］将D-S证据理论引入到协作频谱感知算法，该方法在性能上优于文献［9］采用的准则，但是需获得感知的先验知识，因此具有较高的复杂度。文献［11］采用似然比检测（likelihood ratio test，LRT）的软判决和采用OR准则的硬判决，LRT软判决可以达到更好的感知性能，但在报告信道非理想的情况下，LRT门限仍是一项未解决的难题。文献［12］提出一种更为简单的基于线性加权协作感知模型，该模型为求解最优权重向量，提出一种基于修正偏差因子（modified deflection coefficient，MDC）的方法，但MDC并不能保证得到理论的最优解。而杂草优化算法具有很好的鲁棒性，可通过动态调整正态分布的标准差，使算法在早期、中期充分保持种群的多样性，保证对解空间进行全面搜索。而在后期加强对优秀个体周围的局部搜索，可保稳健收敛到全局最优解。为此，研究了传统杂草优化算法（invasive weed optimiza-tion，IWO），提出了基于改进IWO的协作频谱感知算法，寻找到更好的权重系数，在虚警概率一定的条件下，有效地提高检测概率。

1 系统模型

1.1 线性加权协作频谱感知模型

CR网络中，假设M个认知用户相互协作进行感知，第k时刻各个认知用户的本地感知二元假设检验模型如下：

式中：xl（k）为第l个认知用户接收到的信号，s（k）为授权用户发射的信号，hl为信道衰减因子，vl（k）～CN（0，σl2）为零均值加性高斯白噪声，感知信道的噪声可由σ＝[σ12，σ22，…，σΜ2]T表示。不失一般性，假定vl（k）、s（k）相互独立。H0表示授权频段空闲；H1表示授权频段被占用。该系统模型如图1所示。

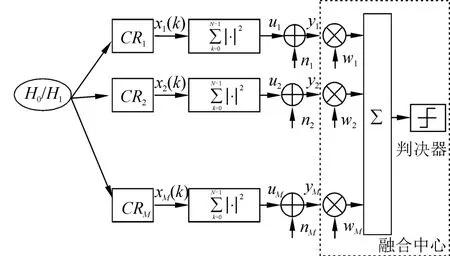
图1 协作感知系统模型

认知用户本地感知均采用能量检测，对接收到的s（k）进行采样，并对所有采样值模求平方和，得到检测统计量ul。

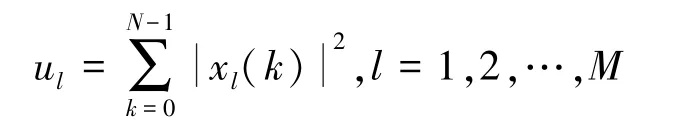
式中N为采样点。

每个认知用户通过控制信道将统计量ul传输给数据融合中心，融合中心收到的统计量为yl：

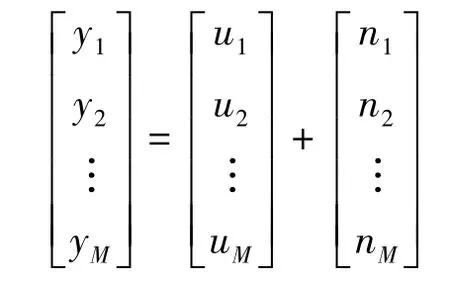
式中：nl为报告信道噪声，服从均值为0、方差为δ2的高斯分布。根据图1，可得融合中心的全局判决统计量yfc。

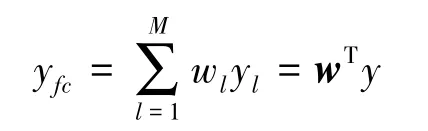
式中：w＝[w1，w2，…，wM]T为权值向量，wM≥0。y＝[y1，y2，…，yM]T为融合中心接收到各个认知用户的本地能量检测的统计量。权重反映各个认知用户对全局判决的影响程度，调整权重系数使接收到的信号的信噪比很高的认知用户分配到大的系数；分配小的权重系数给经受深度阴影和衰落认知用户，以降低它对融合判决结果的影响，提高准确性，使得结果更能反映实际情况。最后，融合中心将yfc与给定的判决器门限γfc进行比较，判决授权用户信号是否存在，实现最终判决。

下面给出该模型下虚警概率Pf和检测概率Pd，公式的推导见参考文献［12］。

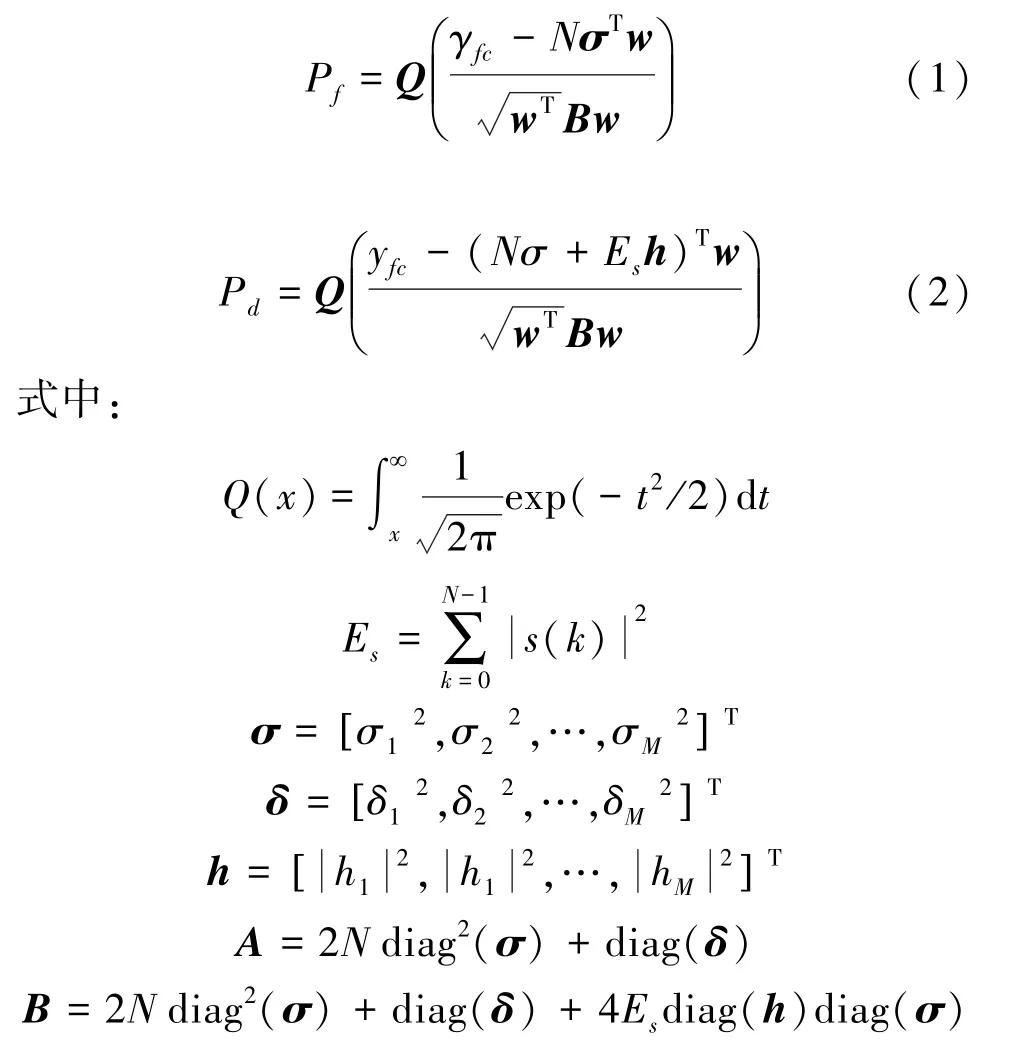
给定虚警概率Pf，门限为γfc：

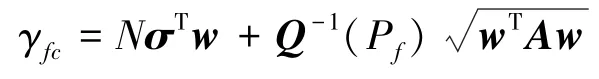
代入式（2），可得

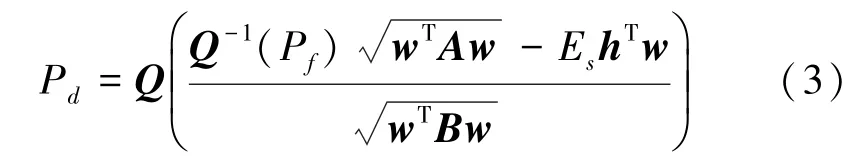
在虚警概率给定情况下，寻找一组权重向量使式（3）最大化，即达到协作频谱感知目的。由于Q函数是单调递减函数，因此将最大化式（3）等效为

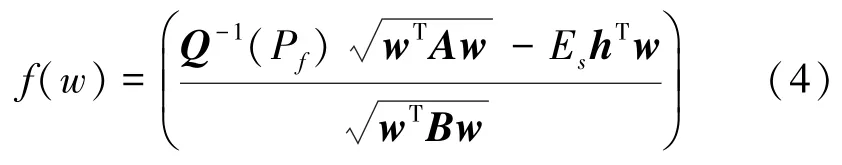
因此，只要找到f（w）的最小值，就可以实现在虚警概率Pf一定下最大化检测概率Pd。

1.2 最优权值求解方法

对于复杂的无线认知环境，直接寻找最优的权重向量w使f（w）达到最小比较困难。文献［12］提出的基于MDC求解w的方法，将f（w）的最小值的求解问题转换为MDC最大化，如下所示：

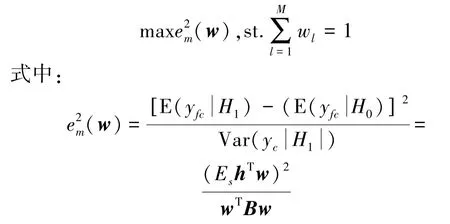
式中：E表示均值，Var表示方差，既而求得的最优权重系数向量：

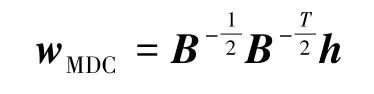
2 基于改进IWO最优线性协作频谱感知

2.1 入侵性杂草优化算法

入侵性杂草优化算法是2006年A.R.Mehrabi-an以及C.Luca受杂草启发而首度提出的，是一种基于种群的数值优化计算方法，能有效解决复杂的非线性工程问题［13-14］。IWO模仿自然界中杂草的种子生成、种子扩散、生长繁殖和竞争消亡过程，具有很强的随机性、鲁棒性和适应性。算法的基本流程分为种群初始化、生长繁殖、空间扩散、竞争排除4个部分，其中种子数量由式（5）确定。

式中：Nseed表示产生的种子数，f表示适应度函数值。个体适应度值与产生种子数成线性关系，S表示产生的种子数。fmax为种群最大的适应度值，fmin代表种群最小适应度值；Smax、Smin分别代表最大、最小种子数，S为可调参数，一般Smin＝1，Smax＝5，足以解决绝大部分最优化问题。

2.2 改进入侵性杂草优化算法的协作频谱感知

改进入侵性杂草的线性协作频谱感知算法直接对f（w）进行优化。频谱感知问题转化为如下带约束条件的优化问题：

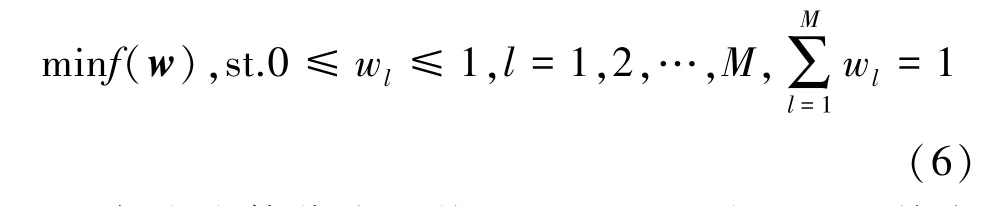
每个个体代表系统的一组权重向量w，其中w＝[w1，w2，…，wM]T，个体维数M代表参与协作频谱感知的用户个数，f（w）为目标函数，种群的初始化按一定的随机方式产生，同时还要保证式（6）的约束条件。本文初始种群的产生，采取每个个体所有元素相对均匀并保证和为1，以缩短算法的搜索时间。

在算法产生种子数前先对目标函数进行降序排列，并对式（5）进行改进，改变传统IWO算法种子产生时单纯的线性关系，增加自适应调整参数q。

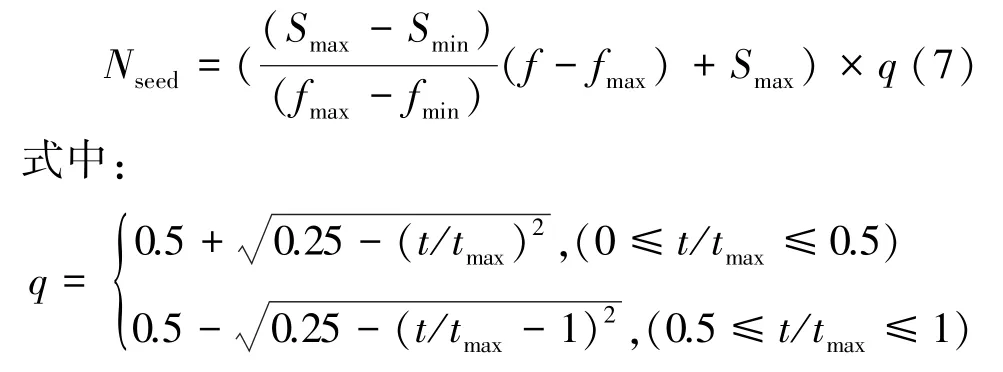
式中：t为当前迭代次数，tmax代表最大迭代次数。改进后的算法从适应度函数值最好的个体开始产生种子，并保证相对大适应度函数数值产生更多的种子，缩短了迭代次数以便更快的找到问题解。图2给出自适应参数q函数图像。

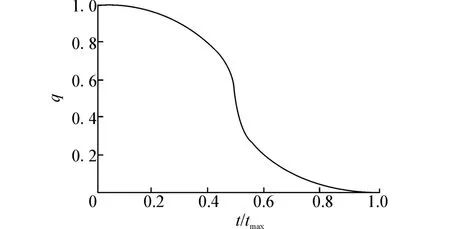
图2 自适应参数q

具体实现步骤如下：

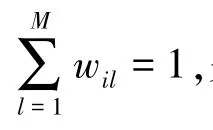
2）由式（4）计算初始种群个体的适应度函数f（w）的值，对其降序排列；

3）按式（7）计算每个个体能产生的种子数；

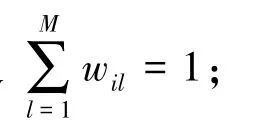
5）把新产生的个体同父代相加，组成新种群，若新种群超出设定的最大种群个体数，则去除适应度函数值较差并且超出种群限定范围的个体，否则跳到步骤6）；

6）若达到最大混合次数，算法终止，否则跳至步骤2）。

3 仿真结果分析

对传统IWO和改进IWO的性能进行比较，初始种群的个体数L＝30，最大种群个体数P＝50，最大迭代次数tmax＝50，调和指数n＝3，假设主用户信号为s（k）＝1，N＝20。图3、4给出了Pf＝0.1时，IWO和改进IWO的目标函数f（w）和检测概率Pd随混合次数的变化曲线，并假设协作认知用户数为M＝6，各个认知用户接收到信号的信噪比分别为9.3、7.8、9.6、7.6、3.5、9.2 dB，δ＝σ＝［1 1 1 1 1 1］T。

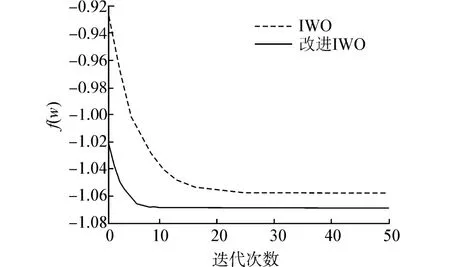
图3 改进IWO与传统IWO目标函数

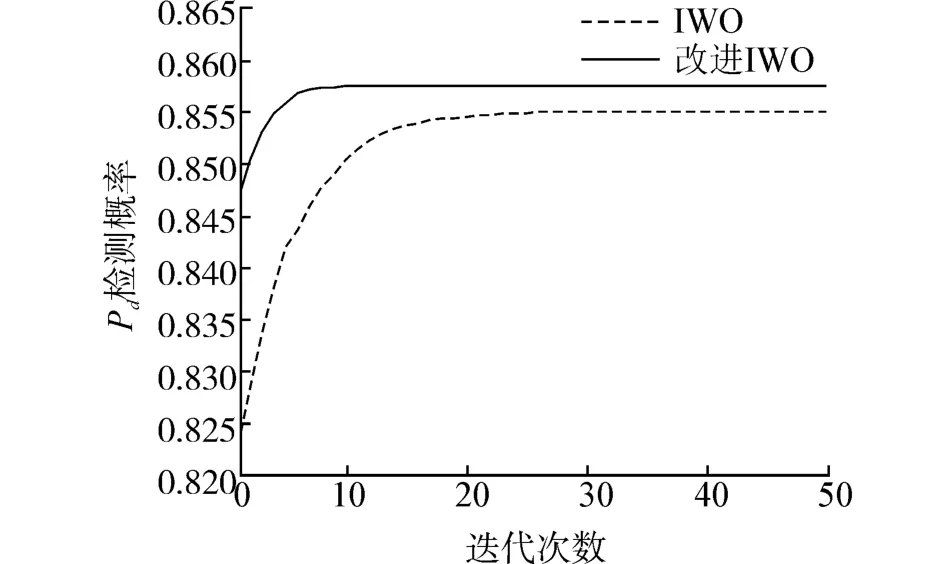
图4 改进IWO与传统IWO检测概率性能比较

传统的IWO算法经过50次迭代，寻找得到的f（w）最小值为－1.061 8，求得相应的Pd值0.855 8，权重系数为［0.208 1 0.146 2 0.227 9 0.148 1 0.088 9 0.180 8］；而改进的IWO算法，寻找到的f（w）最小值为－1.070 0，求得相应的Pd值0.8576，权重系数为［0.206 1 0.157 0 0.217 1 0.151 2 0.066 00.202 5］。可以看出，改进后的IWO算法能以较小的迭代次数找到更优权重向量，检测概率从0.855 8提高到0.857 6。

图5给出不同虚警概率下，改进IWO算法和文献［12］提出的MDC算法的Pd曲线。可以看出，改进IWO算法的检测概率均要略高于MDC算法。其中，各个认知用户接收到信号的信噪比分别为5.3、－2.8、6、7.6、－3.5、－2 dB，M＝6，σ＝［0.9 1.3 1 0.2 0 0.8］T，δ＝［0.4 0.2 0.5 0.4 0.7 0.6］T。

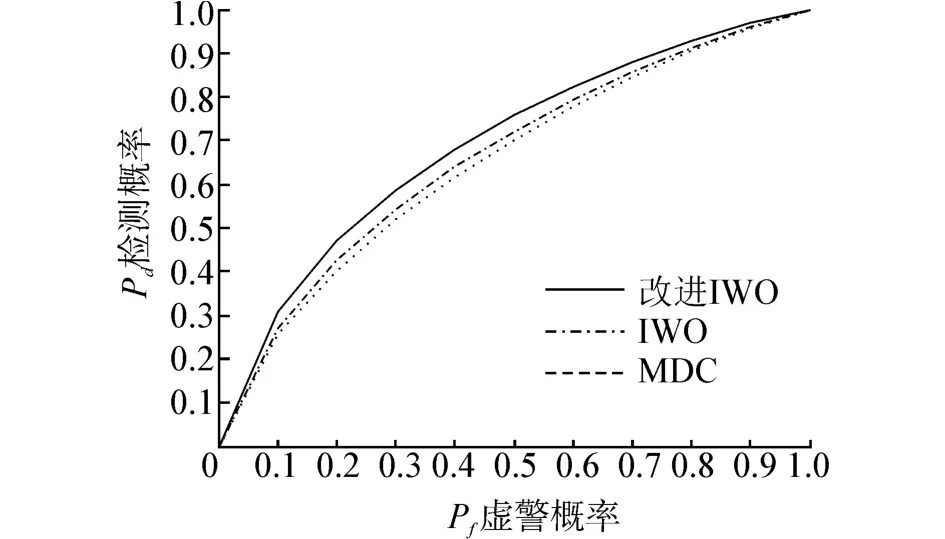
图5 改进IWO与MDC性能比

表1给出了Pf＝0.05，Pf＝0.1以及Pf＝0.2这3种情况下，改进IWO算法与文献［12］中MDC算法的f（w）、Pd数值，仿真条件与图3、4相同。结果亦可以看出改进IWO优化结果均优于MDC算法。

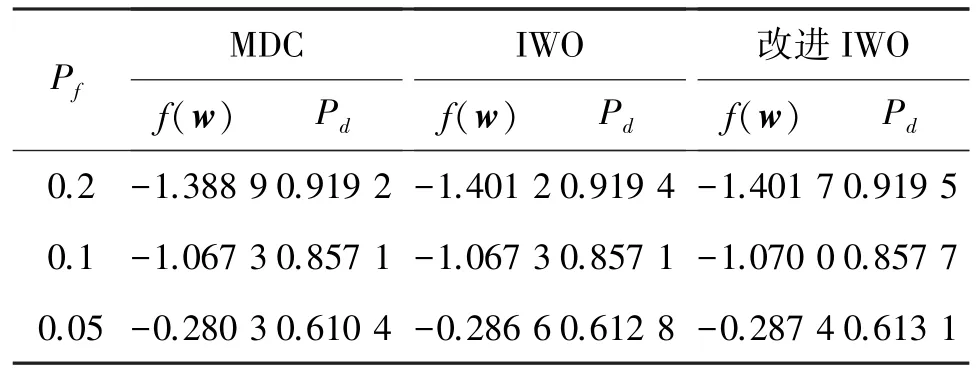
表1 改进IWO与MDC性能比较

表2相应给出3种给定的虚警概率下，改进IWO算法所求的权重向量w的值。可以看出，改进IWO算法可以根据各个认知用户间的不同信噪比很好地调整权重系数，分配较高的系数给接收信噪比高的认知用户，更好地反映当前感知环境的实际情况，从而提高融合判决结果的准确性。

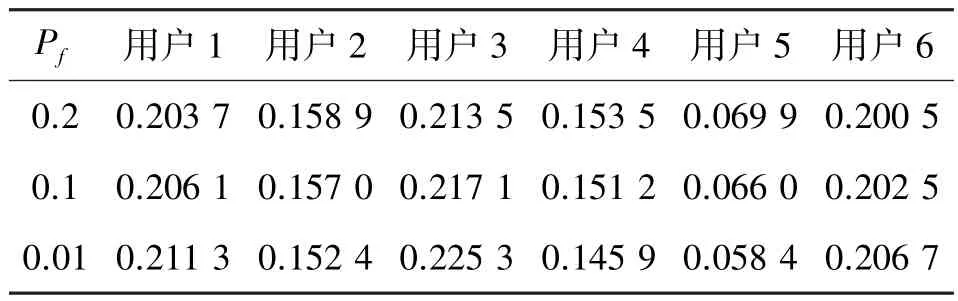
表2 权重系数

图6进一步给出不同噪声环境下漏检概率Pd和虚警概率Pf的性能曲线，其中M＝4，各认知用户接收信号信噪比分别为5.3、－2.8、6、－3.5 dB，δ0＝[0.3 0.9 0.2 0.2]T，σ0＝[0.1 0.3 0.1 0.9]T，3条曲线分别对应（σ＝10σ0，δ＝δ0）、（σ＝σ0，δ＝δ0）和（σ＝σ0，δ＝10δ0）3种噪声环境。

可以看出，随着噪声环境的变化，检测性能降低。检测性能受本地噪声的影响比受报告控制信道噪声的影响更大。

为了进一步研究参与协作频谱感知的认知用户数目对感知性能的影响，设所有情况下认知用户接收SNR取值均为－2 dB，δ＝σ＝[1 1 1 1 1 1]T，图7给出了M＝1、3、8这3种情况下的检测概率Pd曲线。

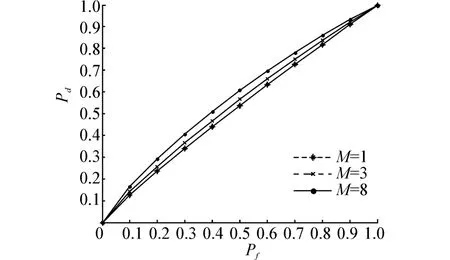
图7 不同认知用户的ROC曲线

可以看出，随着参与协作感知的认知用户数目的增加，检测性能不断提高。在噪声环境较为复杂的条件下，单一用户并不能达到检测效果，多用户协作可以有效地提高感知性能。

4 结束语

文中将改进IWO算法引入最优线性协作频谱感知模型中。改进后的IWO算法在减少迭代次数的同时可以找到比传统IWO更优的目标函数值，并给出最优权重向量。该算法能够更好地根据实际情况分配权重向量，使得该模型下的协作频谱感知结果更准确。对改进IWO算法与基于MDC的协作感知方法性能进行了比较，验证了在相同Pf下改进IWO算法可以获得更小的目标函数值，使得Pd性能变优。分析了不同噪声环境，不同感知用户等条件下对系统性能的影响，检测性能受本地噪声的影响比受报告控制信道噪声的影响更大，而在噪声环境较为复杂的条件下，单一用户并不能达到检测效果，多用户协作可以有效的提高感知性能。

［1］MITOLA J，MAGUIRE G Q.Cognitive radio：making soft-ware radios more personal［J］.IEEE Personal Communica-tions，1999，6（4）：13-18.

［2］MITOLA J.The software radio architecture［J］.IEEE Com-munications Magazine，1995，33（5）：26-38.

［3］王金龙，吴启晖，龚玉萍，等.认知无线电网络［M］.北京：机械工业出版社，2010：64-65.

［4］党建武，李翠然，谢健骊.认知无线电技术与应用［M］.北京：清华大学出版社，2012：78-98.

［5］庾志诚.认知无线电技术的新发展［J］.电信技术，2009，13（1）：111-114.

［6］姜微.基于能量检测的频谱检测技术研究［D］哈尔滨：哈尔滨工程大学，2010：29-35.

［7］王海军，粟欣，王京.认知无线电中的协作频谱检测技术［J］.中兴通讯技术，2009，15（2）：10-14.

［8］陈守坤，李莉，王沛，等.基于阈值选择信噪比的协作频谱检测［J］.通信技术，2011（3）：4-6.

［9］GHASEMI A，SOUSA E S.Collaborative spectrum sensing for opportunistic access in fading environments［C］／／Pro-ceedings of 2005 First IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks.Balti-more，USA，2005：131-136.

［10］PENG Q H，ZENG K，WANG J.A distributed spectrum sensing scheme based on credibility and evidence theory in cognitive radio context［C］／／Proceedings of 2006 IEEE 17th International Symposium on Personal，Indoor and Mo-bile Radio Communications.Helsinki，Finland，2006：1-5.

［11］VISTOTSKY E I，KUFFNER S，PETERSON R.On col-laborative detection of TV transmissions in support of dy-namic spectrum sharing［C］／／Proceedings of 2005 First IEEE International Symposium on New Frontiers in Dynam-ic Spectrum Access Networks.Baltimore，USA，2005：338-345.

［12］QUAN Zhi，CUI Shuguang，SAYED A H.Optimal linear cooperation for spectrum sensing in cognitive radio net-works［J］.IEEE Journal of Selected Topics in Signal Pro-cessing，2008，2（1）：28-40.

［13］MEHRABIAN A R，LUCAS C.A novel numerical optimi-zation algorithm inspired from weed colonization［J］.Eco-logical Informatics，2006，1（3）：355-366.

［14］刘逵，周竹荣.基于野草算法的文本特征选择［J］.计算机应用，2012，32（8）：2245-2249.

Optimal linear cooperation for spectrum sensing based on modified invasive weed optimization algorithm

XIE Wu1，LI Xiao1，LI Ran2
1.College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China 2.Institute of Information Technology，Monash University，Melbourne 3145，Australia

In order to solve the problem of maximizing detection probability，for the given probability of false alarm with the model of linear weighted spectrum sensing using energy detection，a cooperative spectrum sensing strategy based on modified invasive weed optimization（IWO）was proposed.The feasible solution of the algorithm corre-sponds to the weight factor of the spectrum cooperative sensing model.This method maximizes the detection proba-bility by searching the optimal weight vector.At the same time，the results shows that compared with traditional IWO and modified deflection coefficient（MDC），the modified IWO can reasonably distribute system weighting co-efficients according to the current noise environment conditions.It can find a better weight vector in a smaller num-ber of iterations to achieve higher detection probability with its better performance than original scheme of MDC.In conditions of given probability of false alarm，the detection efficiency has been effectively improved by the proposed strategy.

cognitive radio networks；spectrum sensing；optimal linear cooperation；energy detection；invasive weed optimization

TN92

A

1009-671X（2014）05-027-05

10.3969／j.issn.1009-671X.201310002

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1009-671X.201310002.html

2013-10-01.

日期：2014-09-22.

黑龙江省教育厅科学技术研究项目（12533034）；中央高校

基本科研业务费专项资金资助项目（HEUCF130809）.

解武（1967-），男，讲师，博士；

李笑（1988-），女，硕士研究生.

解武，E-mail：xiewu＠hrbeu.edu.cn.