基于时域仿真的船舶电力系统暂态分析
2014-05-15陈立伟汪晨栋冯驰徐玲
陈立伟,汪晨栋,冯驰,徐玲
哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001
基于时域仿真的船舶电力系统暂态分析
陈立伟,汪晨栋,冯驰,徐玲
哈尔滨工程大学信息与通信工程学院,黑龙江哈尔滨 150001
船舶电力系统一般分为发电、配电、输电、用电4个部分。通过研究各部分的运行机理后在MATLAB软件的Simulink环境下,利用模块化的方法,建立了柴油机及其调速系统、发电机励磁系统以及功率负载的仿真模型,进而搭建起船舶电力系统的仿真模型。通过对船舶电站暂态稳定性的特点进行分析,对船舶电力系统的正常运行以及发生的故障的情况进行了仿真并得到仿真结果。结果反映了船舶电站在正常和故障2种状况运行时电网上各部分以及发电机组的电压、电流运行情况,比较准确地反映实际运行中暂态稳定的过程。
船舶电力系统;暂态稳定性;电压;电流;时域仿真
船舶电力系统是船舶系统的重要的组成部分。随着社会发展,各国间的贸易增多,这就要求船舶的载重量也增大。随着超大型船舶更多地被人们采用,超大功率的用电设备在船舶上也得到了广泛应用,因此要求船舶电力系统的容量也要越来越大,以此满足用电设备的用电需求[1]。随着用电设备的增多,船舶电网变得更复杂,对船舶电力系统的管理和控制也更困难,所以船舶电网的供电质量和系统的稳定性越来越受到人们的重视[1-2]。
船舶电力系统的暂态稳定性指的是正常运行的电力系统承受一定大小的、瞬时出现但又立即消失的扰动后,恢复到近似它原有的运行状况的能力;或者这种扰动虽不消失,但系统可从原有运行状况安全地过渡到新的运行状况的可能性,也就是电力系统在急剧扰动下的稳定性[2]。
MATLAB/Simulink作为仿真工具提供了较广泛的应用,可以通过电力系统的电路图自动生成数学模型。利用MATLAB/Simulink可以构建出船舶电力系统的基本模型,然后运用时域仿真的方法来分析船舶电力系统的暂态稳定性[3]。时域仿真法作为分析暂态稳定性的方法之一,具有计算速度快、适应非线性的庞大系统和能给出稳定裕度等优点。针对电力系统的正常运行和故障2种情况分别进行仿真,在时域上清晰的给出系统的暂态过程[3-5]。
1 船舶电力系统的数学模型
1.1 柴油机以及调速器模型
船舶电力系统多用柴油机作为原动机带动同步发电机进行发电。调速器主要由测速器、缓冲器、伺服马达和执行机构4个部分组成,然后加上柴油机一起构成柴油机调速系统[6]。
测速部分的主要传递函数为
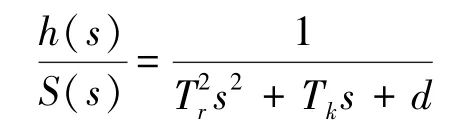
式中:Tr为测速器时间常数;Tk为阻尼器时间常数;d为由滑环行程所确定的位置相对偏差;s为机组的转差率。
伺服马达部分的主要传递函数为

式中:Tσ为导阀的时间常数;β为反馈系数;μ为伺服活塞的相对位移。
缓冲器部分的主要传递函数为

式中:βc为柴油机自调整系数;Ta为时间相对常数。
对各个部分的数学模型进行整合即可以得到柴油机及其调速系统的模型,然后在MATLAB/Simu-link进行搭建,封装得到具有有参数的可视化模块。
1.2 同步发电机及其励磁系统的数学模型
同步发电机的一般描述方法一般分为2种。一种常用的描述同步电机的方法为abc坐标系法,对于空间静止不动的三相坐标系列写方程[7]。另一种是用dq0轴系来表示的磁链电流电压关系方程又称派克变换[8]。对于同步发电机的三相电流两者的变换关系为

式中:a相和d轴之间的夹角为α,q轴超前d轴90°。在用dq0变量的同步电机方程进行分析时,对称条件下不会出现零序量,所以比用abc变量的方程要简单。相应的磁链方程为

式中:f为励磁回路,D、Q为阻尼绕组的等值绕组,式中Ld和Lq分别是定子等效绕组dd和qq的电感系数,称为纵轴同步电感和横轴同步电感。一般将dq0系统中的电势方程和磁链方程合称为同步电机的基本方程,用来描述其特性。
船舶电站上同步发电机的励磁系统多为可控的相复励无刷交流励磁系统,主要包括相复励装置、自动电压调节器和交流励磁机3部分[9-10],其简化的数学模型如图1所示。

图1 励磁系统原理
1.3 负载和网络部分的模型
船舶电力系统的负载主要包括静态负载和动态负载等[7]。静态负载是指船舶的电热和照明设备,占总负荷的比例比较小,采用静态数学模型进行仿真即可;动态负载是指异步电动机拖动装置,如舵机、锚机、水泵、空压机、风机、起货机等,它们的特性各不相同,占总负荷的比例比较大,但总体可以用异步电动机模型来描述[11]。
船舶电站中的负载多为感性负载满组方程:


其变为dq0坐标时的方程为式中:L为绕组电感,r为绕组电阻。
MATLAB/Simulink工具中提供了相应的模块用来描述负载模型。对于网络部分的模型例如输电线路和变压器的模拟,MATLAB/Simulink工具中也提供了可视化的模块,其模型如图2、3所示。

图2 输电线路的可视化模型

图3 变压器的可视化模型
2 时域仿真法的暂态分析
船舶电力系统基本由柴油机及其调速系统、发电机励磁系统、网络和功率负载组成。实际的电网有许多的发电机和负荷通过网络组成,各部分之间互相联系与影响。针对不同的网络结构用时域仿真法来分析暂态过程有以下的优点:l)能获得较好的数值稳定性和计算精度;2)能进行优化以弥补算法本身的缺点;3)能够适用于各种非线性元件和不同规模的系统;4)能辅助对电力系统的各种分析、控制;5)结果直观,信息丰富,能得到各接口变量、状态变量的时间变化曲线和变量之间的关系曲线[12-14]。
利用时域仿真法求解数学模型的过程,实质为在给定的初值条件下,求微分方程的数值解,即为对于离散的时间序列逐步求出相应的系统状态矢量值的过程[15]。在对电力系统进行暂态分析时,主要步骤为:
1)将系统中各元件的微分方程化为tn~tn+1时步的差分方程,包括发电机转子运动方程、发电机转子绕组暂态方程、励磁系统动态方程。
发电机绕组的方程为
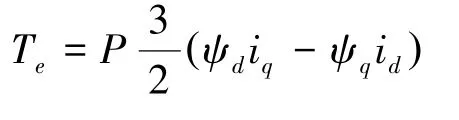
式中:Te表示电磁转矩,P为极对数。发电机转子运动方程为
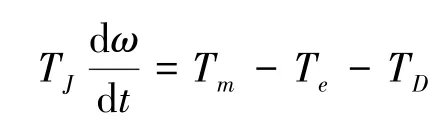
式中:Tm为机械转矩,Te为电磁转矩,TD为阻尼转矩,TJ为机组惯性时间常数。
定子励磁电动势Ef方程为

式中:Xad为电感阻抗,vf为绕组电压,rf为定子每相绕组电阻。
电机q轴空载电动势Eq方程为
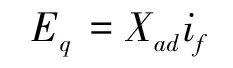
式中:Xad为电感阻抗,if为电流。
电机q轴空载电动势Eq′方程为

式中:ψf为各绕组的总磁链,Xf为电感阻抗。
2)通过上述的差分方程进行消元,只保留元件间的接口变量,而消去元件内部的中间变量。将消元后的差分方程和代数方程联立求解,只保留差分方程和代数方程交界处的变量,即出现在代数方程中的状态量,以便在扰动时进行代数量的跃变计算。
3)通过上述计算将电网中无关的变量消去转化为只关于发电机以及励磁系统、柴油机以及调速系统和负载的可设置的参数变量。即可在外部给定初始值的条件下来进行模型运行过程的仿真,这就是时域仿真暂态过程的基本思路。
船舶电力系统暂态稳定计算的结果可以得到相对的电压、功率、转速随时间变化的曲线,由此来判断系统是否具有暂态稳定性。换句话来说,当系统受到大扰动后,各发电机之间能否继续保持运行,是根据各发电机转子相对角的变化特性来判断整个电力系统的稳定性。即通过对外部系统的参数值进行设置便可以进行计算,在时域上得到关系变化图从而判断电力系统的暂态稳定性[16]。
3 仿真分析
研究船舶电力系统的暂态稳定性可以从许多方面进行下手。引起电力系统大扰动的原因主要有下列几种:1)负载的骤然变化,如投入或断开大容量的功率设备等;2)投入或切除系统的主要元件,如发电机、变压器及线路等;3)线路中某部分发生短路的故障[13]。
当电力系统受到比较大的干扰时,表示系统运行状态的各种电磁参数都要发生急剧的变化[17]。但是由于柴油机及调速器具有相当大的惯性,它必须经过一定时间后才能改变柴油机的功率,于是便产生了不平衡转矩。在转矩作用下发电机开始改变转速,使各发电机转子间的相对位置发生变化,转子的变化反过来又将影响到电力系统中电流、电压和发电机功率的变化[15]。因此由大扰动引起的电力系统暂态过程,是一个电磁暂态过程和发电机转子间机械运动暂态过程交织在一起的复杂过程。同时如果涉及柴油机调速器、发电机励磁调节器等调节设备的暂态过程,则这个过程更加复杂。
针对船舶电力系统的正常运行和故障2种情况,文中分别设计了对应的模型来仿真其暂态稳定的过程。实验仿真环境为Windows 7系统下的MATLAB R2010a。
3.1 投入和切除负荷的系统稳定性仿真
对设计好的船舶电力系统模型进行仿真。开始时发电机组带额定负载稳定运行,然后在电动机稳定后再加上负载,稳定后卸掉负载,观察此系统暂态稳定过程,以此来对应实际应用。发电机组的具体参数数据为:电压400 V、频率50 Hz、功率325 kVA。所带的负载起初功率为10%的动态负载,运行一段时间后加入另一10%的负载,待一段时间后卸除进行仿真,仿真的时间为12 s。观察这段时间内的暂态过程,发电机组的运行情况如图4所示。

图4 发电机组的运行情况
仿真结果显示开始时系统稳定运行,3 s时加上负载,电网电流开始增大,由于发电机端电压无法突变,因此电网消耗的功率加大,要求发电机输出功率加大,发电机的调速系统进行调节,转速逐渐恢复,在5.2 s左右恢复在额定转速,励磁系统进行调节加大励磁电压,使得发电机端电压逐渐回升,发电机功率最后趋于稳定,稳定值大于加上负载之前,因为这时电网消耗的功率增加了;7 s时卸掉该负载,电流减小,发电机组的控制系统工作,发电机各量发生与加载时相反的变化,最后趋于稳定,稳定时功率变小。图中4个数据分别为发电机的功率、励磁电压、端电压和转速,数据均采用标幺制。
3.2 短路故障下的系统稳定性仿真
对于上面的船舶电力系统模型,开始时发电机组带额定负载稳定运行,然后在某时刻电网的某部分发生短路故障,为保护系统,切断了短路部分电网。经一小段时间后系统重新达到稳定状态,观察此系统暂态稳定过程以此来对应实际应用。
图中发电机组的具体参数同上面一样,所带的负载仍为动态负载和静态负载,运行一段时间后发生短路故障,仿真的时间为3 s。观察这段时间内的暂态过程,发电机组的运行情况如图5所示。

图5 发电机组的运行情况
开始发电机稳定运行,0.5 s发生单相接地故障,1 s时故障解除,短路故障发生时发电机转速下降同时调速系统开始工作,但由于故障未切除,转速依然下降,发电机端电压剧烈波动,虽然励磁系统继续工作,但无法电压恢复稳定;故障切除后发电机功率逐渐趋于稳定,转速重新上升,经过2.3 s后逐渐恢复至额定转速,在励磁系统的调解下端电压也逐渐恢复。三相短路时电网的电压和电流分别如图6、7所示。

图6 电网的三相电压变化情况
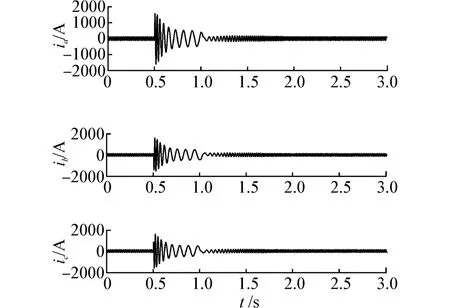
图7 电网的三相电流变化情况
电网发生三相短路时,三相电压全部减小近似为0,电流大幅度增加,导致发电机无法正常工作;将短路故障切除后在发电机的控制系统调节下,发电机的功率、电压和转速逐渐恢复,电网的电压和电流也逐渐恢复。
4 结束语
为了研究船舶电力系统的暂态稳定性,在分析船舶电力系统运行原理的基础上,对其进行建模和仿真。借助了MATLAB软件下的Simulink仿真工具箱,通过可视化的模块将模型搭建起来,然后通过时域仿真的方法来分析了模型的暂态过程,得到了电网参数的变化曲线。仿真结果给出了船舶电力系统在正常工作下和故障运行时,电网各部分的运行情况,通过抽象的仿真可以模拟实际电网的运行的情况,可作为船舶电力系统设计时的参考使用。同时作为参考的仿真结果,进一步验证了模型与算法的有效性。
[1]YANG Xiuxia,ZHANG Yi.Study of shipboard power system intelligent network reconfiguration[C]//Sixth International Conference on Intelligent Systems Design and Applications.Ji’nan,China,2006:1055-1060.
[2]王雪松.船舶应急电站自动控制系统的研究与设计[D].大连:大连海事大学,2010:18-14.
[3]张淑兴.应急柴油发电机组仿真研究[D].大连:大连理工大学,2009:22-27.
[4]吴志良.船舶电站及其自动化系统[M].大连:大连海事大学出版社,2010:34-69.
[5]SUN Wenfu,TENG Wanqing.Application of NetLinx net-work in marine power station monitoring system[C]//27th Chinese Control Conference.Kunming,China,2008:531-535.
[6]于群.MATLAB/Simulink电力系统建模与仿真[M].北京:机械工业出版社,2011:111-132.
[7]王晶,翁国庆,张有兵.电力系统的MATLAB/SIMU-LINK仿真与应用[M].西安:西安电子科技大学出版社,2008:134-145.
[8]王浩亮.船舶电站系统稳定性研究[D].大连:大连海事大学,2010:12-23.
[9]见可可.船舶电站系统的建模与模糊控制研究[D].武汉:武汉理工大学,2012:12-27.
[10]赵云利.船舶综合全电力推进系统的建模与计算机仿真研究[D].哈尔滨:哈尔滨工程大学,2007:29-33.
[11]王斌斌.船舶柴油机转速控制仿真研究[D].大连:大连海事大学,2009:18-23.
[12]周枫.船舶柴油机系统模块化建模与仿真[D].镇江:江苏科技大学,2010:44-47.
[13]CHOI B,CHIANG H.Measurement-based dynamic load models:derivation,comparison,and validation[J].IEEE Transactions on Power Systems,2006,21(3):1276-1283.
[14]CHAN R R,SUDHOFF S D.A linear programming ap-proach to shipboard electrical system modeling[C]//E-lectric Ship Technologies Symposium.Baltimore,USA,2009:261-269.
[15]CHEN H,LU Z.A real shipboard power system and its computer simulation[C]//Power Systems Conference and Exposition.Seattle,USA,2009:1-7.
[16]彭秀艳,于秀萍,王显峰.基于小波分析的电力系统故障检测[J].应用科技,2004,31(2):1-2.
[17]祝贺.船舶电力监控系统设计[D].哈尔滨:哈尔滨工程大学,2009:25-33.
The transient stability analysis of ship power system based on time-domain simulation
CHEN Liwei,WANG Chendong,FENG Chi,XU Ling
College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China
:Ship power system consists of generation,distribution,transmission,and use.By studying the running mechanism of each part and using modular approach,the simulation models of a diesel engine and its speed regula-ting system,generator excitation systems and power loading are established in the MATLAB/Simulink envirinment.On this basis,the ship power simulation system is built up.Through analysis of the ship power transient stability,the characteristics of the normal and failure operations of the ship power system are simulated.The simulation re-sults reflect the voltage and the current operating conditions under normal and failure opeation states of ship power stations,which actually show the process of transient stability during actual operation.
ship power system;transient stability;voltage;current;time-domain simulation
TM935
A
1009-671X(2014)05-014-05
10.3969/j.issn.1009-671X.201310007
http://www.cnki.net/kcms/doi/10.3969/j.issn.1009-671X.201310007.html
2013-10-14.
日期:2014-09-22.
黑龙江省自然科学基金资助项目(F201413).
陈立伟(1974-),女,副教授,博士;
汪晨栋(1988-),男,硕士研究生.
陈立伟,E-mail:chenliwei@hrbeu.edu.cn.
