基于三次非线性忆阻器的有源低通滤波器

欧青立，赵平荣，游淼

湖南科技大学信息与电气工程学院，湖南湘潭 411201

基于三次非线性忆阻器的有源低通滤波器

欧青立，赵平荣，游淼

湖南科技大学信息与电气工程学院，湖南湘潭 411201

忆阻器是具有记忆和连续输出特点的非线性电阻器，现已成为电路中的第4种基本元件。以一个三次光滑的非线性忆阻器模型为基础，与常见的有源低通滤波器相结合，利用电路分析的基本理论，分析该电路的频率响应特性，并与有源RC电路进行对比，对含有忆阻器的有源低通滤波电路进行电路仿真，其结果很好地验证了理论分析。

忆阻器；滤波电路；频率特性；有源低通滤波

自蔡教授在1971年提出忆阻器［1］的概念和定义后，科研人员花费了30多年的时间，终于在2008年，Strukov等［2］首次在实验室通过纳米技术实现了物理忆阻器。忆阻器被实现以来，关于忆阻器和忆阻器电路应用得到了很大地发展，其应用价值引起了国内外许多学者的兴趣：利用忆阻器的数字工作方式，可以制作非易失性阻抗存储器（RRAM）［3］，纳米忆阻器以及相关器件的物理实现［2］，忆阻器的建模以及电路特性研究［4-6］，忆阻混沌电路及动力学研究［7-11］等。忆阻器已经被国际上公认为第4种基本电路元件，所以有必要对其在电路中的基本特性进行建模和电路仿真研究。基于此，通过理论分析忆阻器的特性，建立一个三次光滑的忆阻模型，然后利用其取代有源低通滤波电路中的电阻来分析忆阻器在滤波电路的特性和应用前景。

1 磁控忆阻器的建模以及电路实现

1.1 磁控忆阻器的建模

忆阻器是一个两端元件，在文中用M表示其在电路中的符号，其忆阻值是由磁通量与通过其两端的电荷来决定，如式（1）所示：

式中W（φ）为忆阻器的忆导值。通过忆阻器两端的电压v（t）和电流i（t）的关系如式（2）所示：

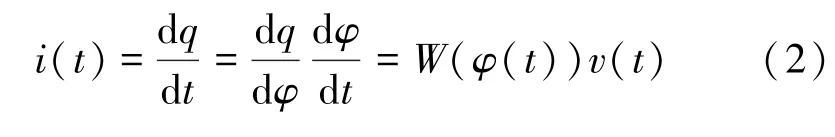
式中W（φ（t））＝W（∫v（t）），从忆导值的积分∫v（t）算子中，可以得出忆阻器对过去电压的状态具有依赖性，即为忆阻器的本质体现。

综合分析HP忆阻器的模型［2］和蔡教授提出的PWL模型［12］，文献［13］的乘法芯片AD633的电路如图1所示。

图1 AD633电路

设置AD633的增益为10，则可以得出W端输出的电压方程为

利用基尔霍夫定律可以得出电流的方程：

设当V1＝V2和V1＝V22时，可以得出：

由式（5）、（6）可以得出一个普适的三次非线性曲线方程如下：

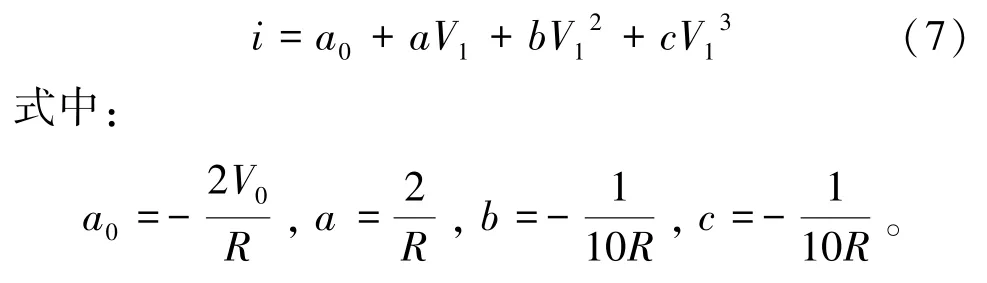
基于此，这里选择一个三次非线性作为q－φ的函数，方程如式（8）所示：

因此由式（8）可以得出忆阻器的忆导值为

1.2 三次非线性忆阻器模型的电路实现

利用电路中的常见元件搭建式（4）的电路模型，该电路模型由3个运算放大器、2个乘法器、6个电阻以及1个电容构成，电路图如图2所示。

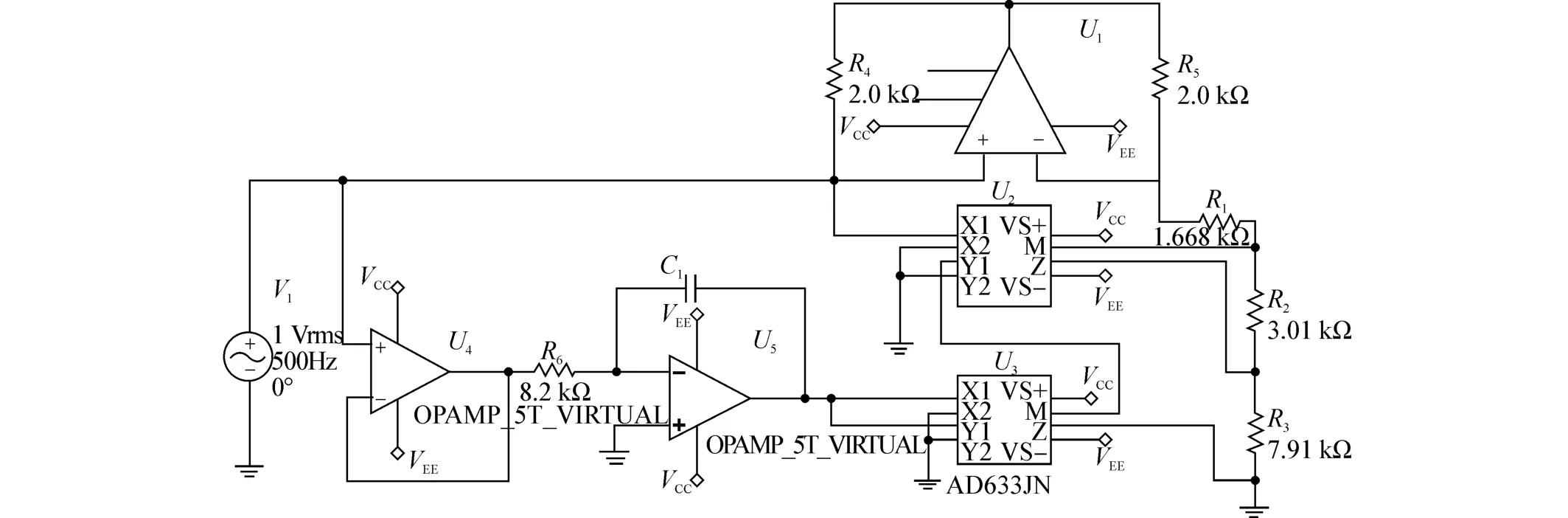
图2 三次非线性忆阻器的仿真电路

在图2中，VCC＝15 V，VEE＝－15 V，AD633JN乘法器的增益设置为10，根据文献［13］可以计算该电路的电压和电流的关系为

由电压与磁通量的关系可以得出：

结合式（10）和（11）得出：

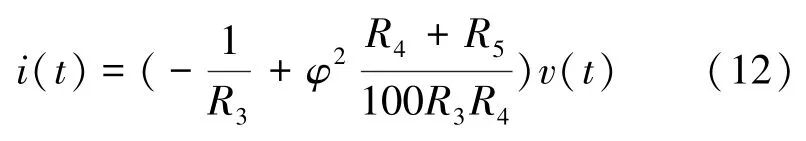
比较式（2）、（9）、（10），可以得出：

2 基于忆阻器的一阶有源低通滤波电路

2.1 电路仿真

图3所示为RC一阶有源低通滤波电路，设置参数Rf＝1 kΩ，R1＝1 kΩ，R＝1 kΩ，C＝0.25 μF，可得出增益A＝2，截止频率f0＝639.94 Hz，仿真电路以及交流分析如图3所示，其在不同频率的输入信号下的滤波如图4所示。

图3 一阶RC有源低通滤波电路

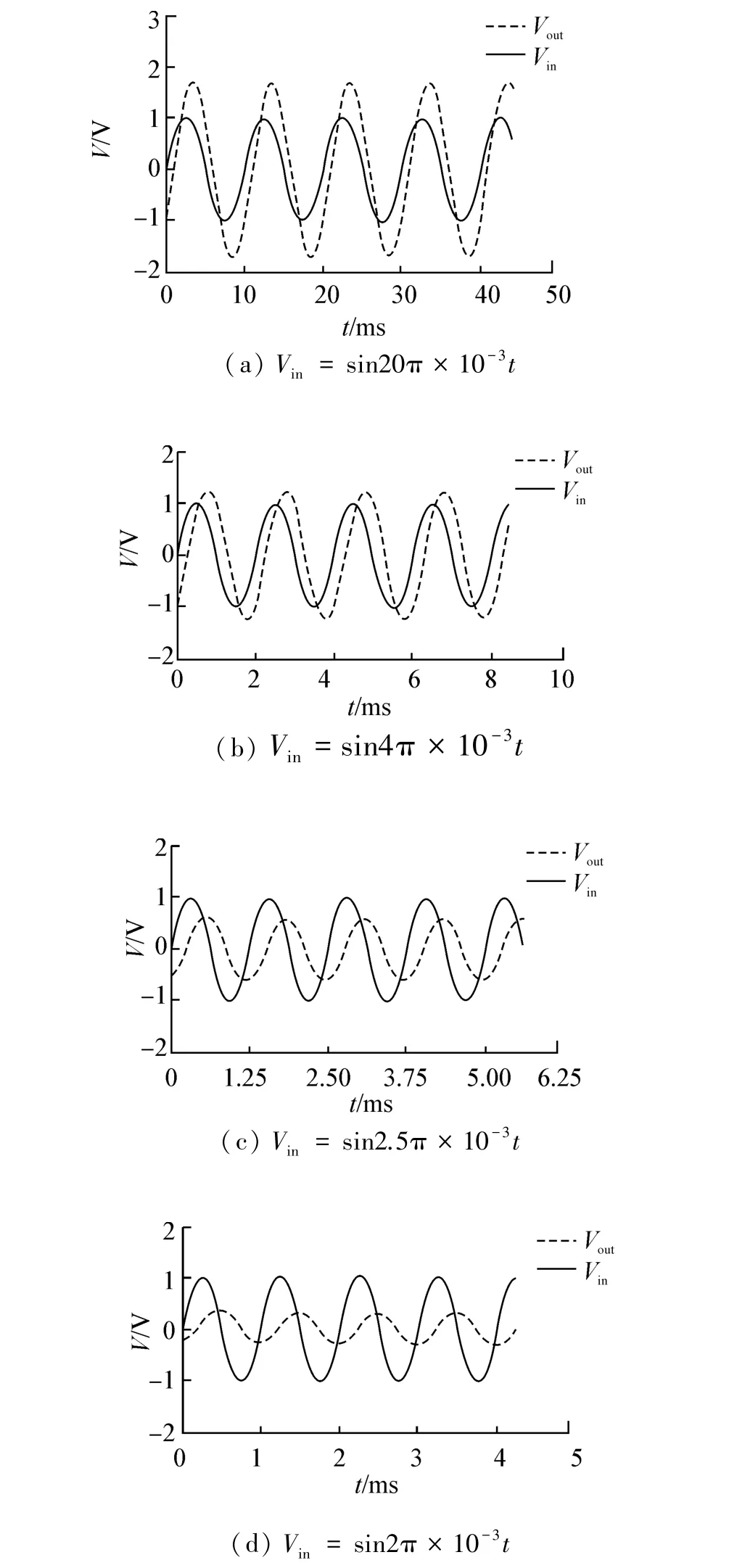
图4 一阶有源RC低通滤波电路时域

一阶RC有源低通滤波电路的时域仿真结果如表1所示。

表1 一阶有源RC低通滤波电路时域仿真结果

从图4和表1中可知，当输入电压的频率逐渐增加以后，输出电压会逐渐的减弱，直至不能输出，故为低通选频。

滤波器是一种能使有用频率信号通过而同时抑制无用频率信号的电子装置，常用于信号处理、数据传输和干扰抑制等方面。一阶有源低通滤波电路由集成运放和无源元件电阻和电容构成。它的功能是允许从零到某个截止频率的信号无衰减地通过，而对其他频率的信号有抑制作用，有源滤波器能够在滤波的同时对信号起放大作用，这是无源滤波无法做到的［14-15］。

现用上述忆阻器模型来建立一个有源MC低通滤波电路，其仿真电路如图5所示。设置输入电压v（t）＝sint，取零状态φ（0）＝0，由式（9）和（11）以及欧姆定律可以得出：

由式（14）中可得忆阻器M的忆导值为

从M的忆导值可以得出，图5电路的传递函数中包括时间因子t，因此该电路是一个时变系统，不能直接通过系统传递函数来描述MC有源低通滤波电路特性。

进而分析该电路的时域滤波特性，设置仿真参数如下：R1＝1.5 kΩ，R2＝3 kΩ，R3＝36 kΩ，R4＝2 kΩ，R5＝2 kΩ，R6＝1 kΩ，R7＝1 kΩ，R8＝8.2 kΩ，R9＝1 kΩ，C1＝0.25 μF，C2＝47 nF，VCC＝15 V，VEE＝－15 V。通过计算得出一阶MC有源低通滤波电路的截止频率：f0＝640.12 Hz，增益A＝2。该电路在不同频率下的滤波时域如图6所示。

图5 一阶有源MC低通滤波电路

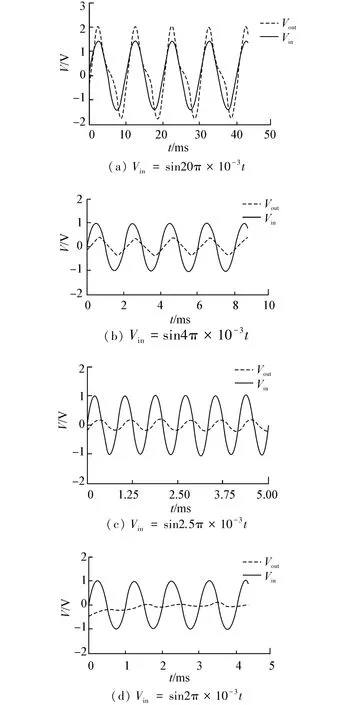
图6 一阶有源MC低通滤波电路时域

一阶有源MC低通滤波电路的时域仿真结果如表2所示。MC有源滤波电路特性不仅由M和C决定，还包括输入电压的频率以及时间因子，这是由于忆阻器阻值受时间因子决定的。对比RC滤波电路在同等参数条件下，当f≤f0时，一阶RC滤波电路和一阶MC滤波电路输出相对误差分别为1.0%和3.3%；而当f≥f0时，一阶MC滤波电路和一阶RC滤波电路的输出电压相对误差分别为10.1%、38.7%，即一阶MC滤波电路的斩波幅度明显高过一阶RC滤波电路。

表2 一阶有源MC低通滤波电路时域仿真结果

2.2 频域滤波特性分析

图7 一阶有源RC低通滤波器波特图

图8 一阶有源MC低通滤波器波特图

在同参数的条件下，一阶有源MC低通滤波电路的选频特性比一阶有源RC低通滤波电路更好。对于f≤f0的低频信号，一阶有源MC低通滤波电路具有与一阶RC电路相同的选通特性；而对于f≥f0的高频信号段，一阶MC电路的衰减的速度明显高过RC电路。从以上理论分析和仿真数据分析可以得出：一阶MC滤波电路完全能够取代一阶RC滤波电路，在斩波方面比一阶RC滤波电路的效果还要明显。

3 结束语

在分析各个忆阻器模型以及工作原理的基础上，提出一个容易实现的三次非线性忆阻器模型，并将该模型应用于一阶有源MC低通滤波电路中，通过理论分析其在一阶有源MC滤波电路中的电路特性，配置一定的参数，用仿真电路验证理论分析。仿真结果表明，数值仿真和理论分析很好地吻合，进一步说明可以用忆阻器来代替一阶有源MC低通滤波电路中的滤波电阻，由于忆阻器为纳米级的元件，用一阶MC滤波电路来取代一阶RC滤波电路，可以提高电路的集成度。

［1］CHUAL O.The missing circuit element［J］.IEEE Trans Circuit Theory，1971，18（5）：507-519.

［2］STRUKOV D B，SNIDER G S，STEWART D R，et al.The missing memristor found［J］.Nature，2008，453：80-83.

［3］胡小方，段书凯，王丽丹，等.脉冲控制忆阻模拟存储器［J］.电子科技大学学报，2011，40（5）：642-647.

［4］BENDERLI S，WEY T A.On SPICE macromodelling of TiO2memristors［J］.Electron Lett，2009，45（7）：377-379.

［5］JOGLEKAR Y N，WOLF S J.The elusive memristor：prop-erties of basic electrical circuits［J］.Euro J Phys，2009，30（4）：661-675.

［6］RIAZA R.Nondegeneracy conditions for active memristive circuits［J］.IEEE Trans Circuits and Systems II，2010，57（3）：223-227.

［7］MUTHUSWAMY B.Implementing memristor based chaotic circuits［J］.Int J Bifurcation and Chaos，2010，20（5）：1335-1350.

［8］BAO B C，LIU Z，XU J P.Steady periodic memristor oscil-lator with transient chaotic behaviors［J］.Electron Lett，2010，46（3）：228-230.

［9］BAO B C，XU J P，LIU Z.Initial state dependent dynami-cal behaviors in memristor based chaotic circuit［J］.Chin Phys Lett，2010，27（7）：070504.1-070504.3.

［10］BAO B C，MAZ H，XU J P，et al.A simple memristor chaotic circuit with complex dynamics［J］.Int J Bifurcation and Chaos，2011，21（9）：2629-2645.

［11］齐爱学，卞丽，李卫兵.基于记忆电阻的Chua混沌电路的实现及动态性能分析［J］.中国海洋大学学报，2011，41（6）：119-124.

［12］CHUA L O，KANG S M.Memristive devices and systems［J］.Proceedings of the IEEE，1976，64（2）：209-223.

［13］ZHONG G.Implementation of Chua’s circuit with a cubic nonlinearity［J］.IEEE Trans Circuits Syst，1994，41：934-941.

［14］ITOH M，CHUA L O.Memristor oscillators［J］.Interna-tional Journal of Bifurcation and Chaos，2008，18（11）：3183-3206.

［15］WANG Weidong，YU Qin，XU Chunxiang，et al.Study of filter characteristics based on PWL memristor［C］／／Inter-national Conference on Communications，Circuits and Sys-tems.Milpitas，USA，2009：969-973.

Active low-pass filter characteristics based on the cubic nonlinear memristor

OU Qingli，ZHAO Pingrong，YOU Miao
School of Information and Electrical Engineering，Hunan University of Science and Technology，Xiangtan 411201，China

The memristor is a nonlinear resistor as the fourth ideal circuit element，and it has the function of remem-bering the history state and continuous output characteristics.The active low-pass filter characteristics based on the cubic nonlinear memristor is studied，and the frequency response of this circuit is analyzed.Through simulating the active low-pass filter circuit with the memristor，experimental results verify the theoretical analysis well in compari-son with the active low-pass RC filter circuit.

memristor；filter circuit；frequency characteristics；active low-pass filter

TM132

A

1009-671X（2014）05-006-05

10.3969／j.issn.1009-671X.201312016

2013-12-28.

国家自然科学基金资助项目（11272119）；湖南省自然科学基金资助项目（14JJ2099）；湖南省工业科技支撑计划项目（2011GK3160），湖南科技大学研究生创新项目（S120020）.

欧青立（1962-），男，教授；

赵平荣（1987-），男，硕士研究生.

赵平荣，E-mail：409562347＠qq.com.