管道多单元磁轭法轴向磁化有限元分析和设计

，，，

（海军工程大学 动力工程学院，武汉 430033）

铁磁性管道广泛应用于冶金、石油和化工等行业，其质量和安全问题一直是人们关注的热点，作为一种强有力的探伤手段，电磁检测已广泛应用于各种铁磁性构件的检测［1－2]。其中，对铁磁材料进行磁化在电磁检测中占有重要地位，磁化合适与否严重影响着检测灵敏度和检测可重复性［3]。在过去的研究工作中，人们在研究裂纹的深度、宽度对磁化场的影响方面做了大量工作，但对磁化及磁路设计方面做的工作不多［4－6]。被测构件的磁化由磁化器实现，主要包括磁场源和磁回路等几个主要部分，针对被检测构件的结构特点，选择源磁场和设计磁回路是磁化器优化设计的关键［7]。

电磁检测中选择合适的磁化方法在磁化器结构设计中非常重要［8]。常用的磁化方法有交流磁化、永磁磁化和直流磁化。交流磁化易产生集肤效应，磁化深度有限；永磁磁化磁化强度不便于调节；直流磁化可根据对磁化程度的要求调节磁化强度［9]。综合比较以上三种方法，可以采用直流磁轭法对管道进行轴向磁化。考虑到单个单元的轴向磁化只能对管道进行一定圆周角度范围内的磁化，故采用8组磁化单元，沿管道圆周方向等距分布，这样可以对整个圆周进行磁化。传统的管道磁化方法局限于局部点或面的磁化或者线圈的圆周磁化。局部点或面的磁化效率低，容易漏检；线圈磁化只适用于两端有开口的管道，对于两端没有开口的管道，线圈无法套到管道上，故无法对管道进行磁化。而多单元磁轭法轴向磁化器可做成卡带式，对于没有开口的管道可从中间卡在管道上，并可以根据管道外径的变化增加或减少电磁铁的数目，通用性强。

1 管道磁化有限元模型的建立和求解

1.1 磁轭法磁化的基本数学方程

磁轭上缠绕的线圈叫做螺线管。设螺线管的半径为R，总长度为L，单位长度内的匝数为n，若取轴与螺线管的轴线重合，其中点设为原点O，设螺线管轴线上点P坐标为x，整个螺线管在P点产生的总磁场为：

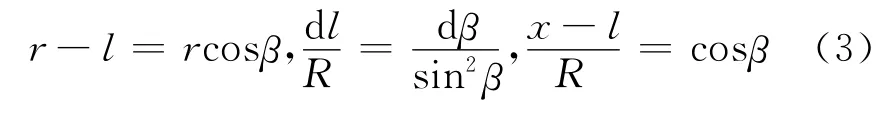
则有

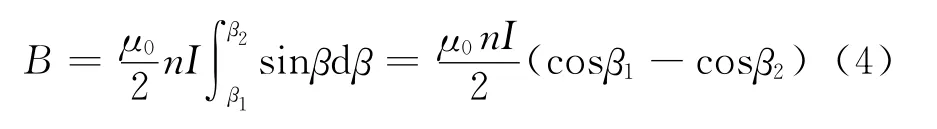
式中：β1，β2分别为β角在螺线管两端的数值。

对于闭合磁化磁路，由安培环路定律可得［10]：

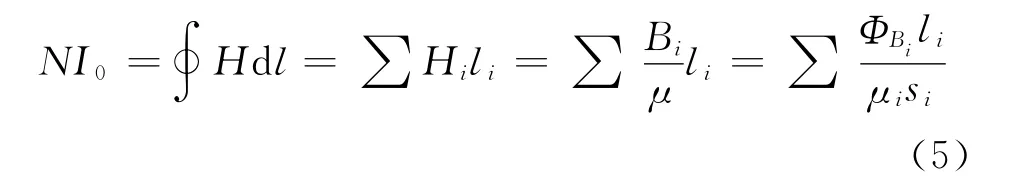
式中：N，I分别为产生磁化场的线圈匝数和传导电流；Hi，Bi，ΦBi，μi，l i，si分别为第i段均匀磁路中的磁场强度、磁感应强度、穿过的磁通量、磁导率、长度和截面积，积分回路L沿着磁路选取。

1.2 建立有限元模型和求解

只对局部管道、磁化结构及外层空气进行建模，这样既有利于网格的合理划分，又节省了计算时间。其中管道尺寸为φ273 mm×14 mm，材料为20钢，铁芯材料为纯铁，加载10 A的电流，线圈匝数为500匝，铁芯截面积为50 mm×50 mm，接触面气隙为5 mm，线圈安匝数为5 000安匝。采用三维静态标量法分析，磁标量位方法将电流源以基元的方式单独处理，无需为其建立模型和划分有限元网格。定义材料类型为SOLID96，其形状为六面体，有8个节点，使用RSP法求解。对于管道采用扫掠划分方式，由于其它结构的复杂性，故采用自由划分方式，设置网格智能化控制疏密等级为4，选取网格形状为四面体。得到磁化模型磁感应强度的结果云图，如图1所示。

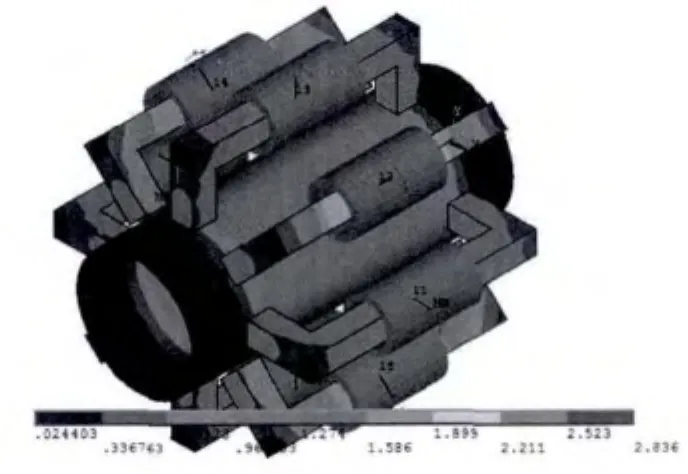
图1 磁化模型的磁感应强度云图

从图1中可以看出，磁轭法磁化的磁感应强度最大值位于线圈包裹的铁芯处，铁芯两轭之间管道的磁感应强度较大且比较均匀；而铁芯两轭之外的管道部分磁感应强度很小。

2 参数对管道磁化场的影响

从线圈安匝数、铁芯截面积以及接触面气隙三个方面探讨不同参数对管道磁化场的影响，得出相应规律从而为磁化器的设计提供理论指导。

2.1 线圈安匝数对管道磁化场的影响

保持铁芯截面积为50 mm×50 mm，接触面气隙为5 mm不变，将线圈安匝数依次设置为2 500，3 750，5 000，6 250，7 500安匝，沿管道外壁轴向建立路径，得到管道外壁沿轴向方向的磁感应强度分布，如图2所示。取管道均匀磁化部位所有数据的平均值，得到不同安匝数所产生的管道均匀磁化部位的平均磁感应强度值，如图3所示。

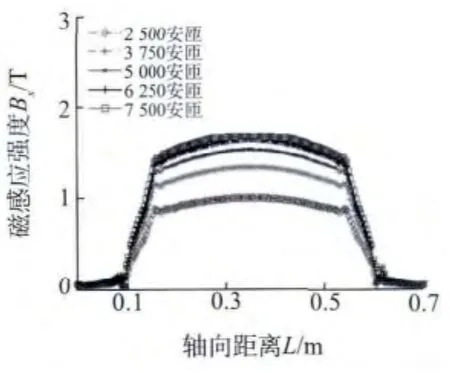
图2 不同线圈安匝数的管道磁感应强度分布

由图2可以直观地看出，管道两端的磁感应强度值很小，在磁轭处发生突变，中间部分的磁感应强度较大，并且比较均匀，这一部分是磁化的有效区域。由图3可以看出，随着安匝数的增大，管壁的平均磁感应强度呈现非线性增加，并且在达到6 250安匝后增长十分缓慢，出现饱和。这是由于铁芯和管道磁化曲线的非线性造成的。综合考虑线圈加载电流和线圈体积限制，设计时线圈采用5 000的安匝数。

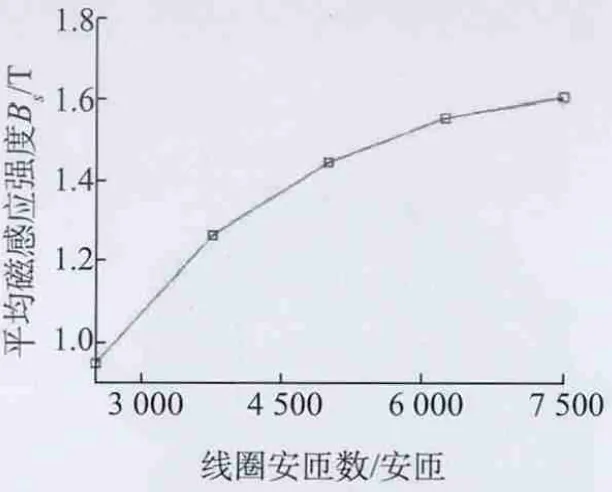
图3 线圈安匝数对管道磁感应强度的影响

通过曲线拟合可得到线圈安匝数与管道平均磁感应强度关系的经验公式：

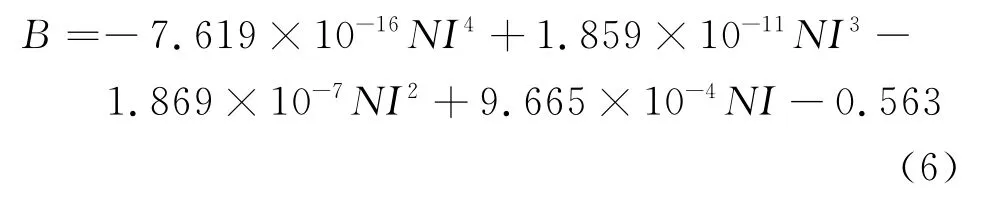
式中：B为磁感应强度，T；NI为线圈安匝数。

从上面的经验公式可以看出，在保持铁芯截面积，接触面气隙不变的情况下，磁感应强度与线圈安匝数呈非线性增长关系，根据经验公式可知，当我们改变线圈安匝数时可以估算磁感应强度。

2.2 铁芯截面积对管道磁化场的影响

保持线圈安匝数为5 000安匝，接触面气隙为5 mm不变，将铁芯截面积依次设置为20 mm×20 mm，30 mm×30 mm，40 mm×40 mm，50 mm×50 mm，60 mm×60 mm，得到管道外壁沿轴向方向的磁感应强度分布，如图4所示；得到不同铁芯截面积所产生的管道均匀磁化部位的平均磁感应强度值，如图5所示。

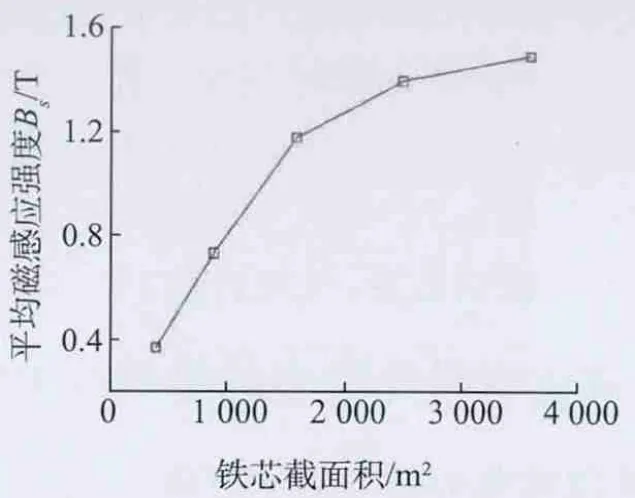
图5 铁芯截面积对管道磁感应强度的影响

可以看出，一开始在管道磁化曲线的线性区，随着铁芯截面积的增大，管道平均磁感应强度呈线性增加趋势，当进入管道磁化曲线的非线性区，随着铁芯截面积的增大，管道平均磁感应强度呈非线性增加趋势。综合考虑铁芯体积、质量以及管道的磁化效果，设计时采用50 mm×50 mm的截面积。

通过曲线拟合可得到铁芯截面积与管道平均磁感应强度关系经验公式：

式中：S为铁芯截面积，mm2。

从上面的经验公式可以看出，在保持线圈安匝数，接触面气隙不变的情况下，磁感应强度与铁芯截面积呈非线性增长关系，根据经验公式，当改变铁芯截面积时可以估算磁感应强度。

2.3 接触面气隙大小对管道磁化场的影响

保持线圈安匝数为2 500安匝，铁芯截面积为50 mm×50 mm不变，将接触面气隙厚度依次设置为1，2，3，4，5 mm，得到管道外壁沿轴向方向的磁感应强度分布，如图6所示。得到不同匝数所产生的管道均匀磁化部位的平均磁感应强度值，如图7所示。

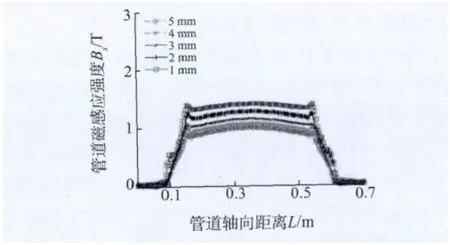
图6 不同接触面气隙厚度的管道磁感应强度分布

可以看出，随着气隙厚度的减小，管道平均磁感应强度逐渐增大，并且呈非线性增大趋势，气隙厚度越小，管道平均磁感应强度增加越多。在实际磁化器的设计时，要尽量减少接触气隙厚度，以达到更好的磁化效果，考虑到铁芯很难完全与管道无缝接触，设计时采用1 mm的气隙厚度。

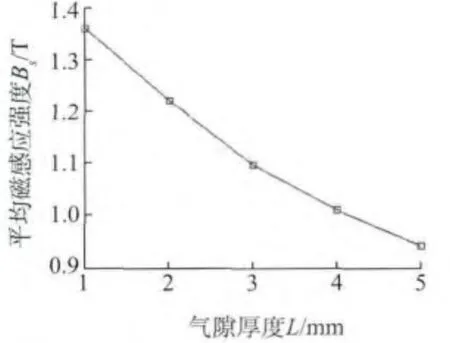
图7 接触面气隙厚度对管道磁感应强度的影响

通过曲线拟合可得到接触面气隙厚度与管道平均磁感应强度关系经验公式：

式中：L为气隙厚度，mm。

从上面的经验公式可以看出，在保持线圈安匝数、铁芯截面积不变的情况下，磁感应强度与气隙厚度呈非线性减小关系，根据经验公式，当改变气隙厚度时可以估算磁感应强度。

3 柱状缺陷与裂缝缺陷的漏磁场分布

为进一步探讨该磁化器的磁化效果，在完整管道上分别制作一个柱状缺陷和周向裂缝缺陷，数值仿真计算缺陷处的漏磁场分布，通过观察缺陷处的漏磁场分布来判定该磁化器是否达到磁化效果。

所建圆柱缺陷半径为10 mm，在柱状缺陷上方2 mm处，以圆柱形缺陷竖直对称轴为中心沿管道轴向向两侧各自延伸30 mm，得到圆柱形缺陷处的漏磁场分布，如图8所示。所建周向裂缝缺陷轴向宽度为6 mm，深度为7 mm，以裂缝缺陷对称轴为中心沿管道轴向向两侧各自延伸30 mm，得到裂缝缺陷处的漏磁场分布，如图9所示（Bx，By，Bsum分别表示磁感应强度x方向分量，y方向分量和矢量和）。

图8 圆柱形缺陷的漏磁场分布

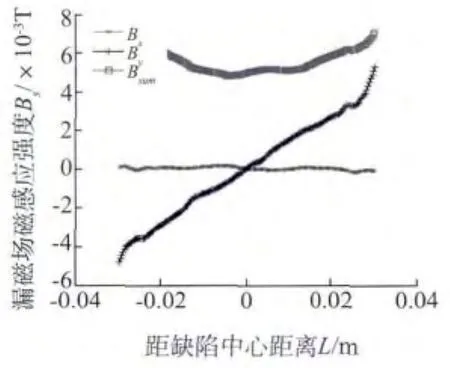
图9 裂缝缺陷的漏磁场分布

由图8可以看出圆柱形缺陷处的磁感应强度值发生明显的变化，并以缺陷中心为中心对称分布。其中磁感应强度矢量和在缺陷处出现一个峰值，在缺陷中心处出现最大值；磁感应强度x方向分量数值很小，几乎为零，在缺陷处并没有太大变化；磁感应强度y方向分量分布呈N字形，在缺陷边缘出现一个峰值，随后随着靠近缺陷中心不断变小，在缺陷中心处变为零，接着随着远离缺陷中心，变为负值，磁感应强度方向发生变化，其绝对值一直增加直到缺陷边缘处达到最大。

由图9可以看出周向裂缝缺陷处的磁感应强度分布也呈对称分布。其中磁感应强度矢量和在缺陷处出现一个峰值，在缺陷中心处出现最小值；磁感应强度x方向分量数值很小，几乎为零，在缺陷处并没有太大变化；磁感应强度y方向分量分布呈斜线分布，在缺陷中心处出现磁感应强度的方向变化。

以上圆柱形缺陷处和周向裂缝缺陷处磁感应强度的变化很好地说明了该磁化方式对圆柱形缺陷和周向裂缝缺陷检测的可行性，证明了磁化器磁化效果良好。

4 结论

磁化器安匝数越大，管道磁感应强度越大，当管道磁饱和时增长缓慢；铁芯截面积越大，管道磁感应强度越大，在管道未达到饱和时，呈线性增加趋势；接触面气隙对管道磁感应强度的影响是非线性的，气隙厚度越小，管道磁感应强度越大，而且气隙越小管道磁感应强度增加的越多。得到了圆柱形缺陷和周向裂缝缺陷处的漏磁场分布，漏磁场分布在两种缺陷处都发生变化，其中磁感应强度y方向分量在缺陷中心处发生方向变化，这可以很好的证明多单元磁轭法轴向磁化电磁检测的可行性，为磁化器的设计提供了理论指导作用。

［1]胡浪涛，何辅云.管道漏磁检测磁化系统研究和设计［J].电子测量与仪器学报，2008，22（6）：102－107.

［2]戴光，孙传轩，杨志军，等.管道外壁缺陷多磁化单元磁场数值模拟与参量分析［J].压力容器，2008，25（11）：24－29.

［3]孙燕华，康宜华，石晓鹏.基于单一轴向磁化的钢管高速漏磁检测方法［J].机械工程学报，2010，46（10）：8－13.

［4]JANSEN H J M ，CAMP P B J，GEERDINK M.Magnetisation as a key parameter of magnetic flux leakage pigs for pipeline inspection［J].Insight，1994，36（9）：672－677.

［5]黄松岭.管道磁化的有限元设计［J].清华大学学报：自然科学版，2000，40（2）：67－69.

［6]ATHERTON D L.Stress－shadow magnetic inspection technique for far－side anomalies in steel pipe［J].NDT International，1983，16（6）：145－149.

［7]ALTSCHULER E，PIGNOTTI A.Nonlinear model of flow detection in steel pipes by magnetic flux leakage［J].NDT International，1995，28（1）：35－40.

［8]康宜华，武新军，杨叔子.磁性无损检测技术中的磁化技术［J].无损检测，1999，21（5）：206－209.

［9]高廷岩.管外多磁化单元结构优化设计与实验研究［D].大庆：东北石油大学，2011.

［10]任吉林，林俊明.电磁无损检测［M].北京：科学出版社，2008.