Fe3Al合金表面偏析的Monte Carlo模拟研究

邓辉球



Fe3Al合金表面偏析的Monte Carlo模拟研究

邓辉球*

(湖南大学 应用物理系, 湖南 长沙, 410082)

应用改进分析型EAM理论和Monte Carlo方法模拟研究了温度从700～1 400 K时Fe3Al合金(100)和(110)面的表面成分和剖面成分分布情况, 发现在合金不同的表面方向, Al在表面偏析, Fe在次表面偏析, 剖面成分呈振荡分布. 在(100)方向, 模拟发现Fe3Al合金高温时发生有序-无序转变. 在(110)方向发现温度较高时计算的表面Al含量比实验测量值低, 温度较低时计算结果与实验结果符合得很好.

表面偏析; Fe3Al合金; Monte Carlo模拟

早在20世纪50年代人们就已经发现金属间化合物作为高温结构材料具有特殊的性能. 与常规铁基合金相比, Fe3Al金属间化合物比重小、弹性模量高、抗氧化、耐热腐蚀, 而且价格便宜. 在低于600 ℃的温度下, Fe3Al的屈服强度随温度的升高而提高. 但是其室温脆性及600℃以上时力学性能的不足, 成为其作为工业合金应用的障碍. 近十年来, 由于Fe3Al环境氢脆机制以及改善Fe3Al室温塑性等方面的研究取得重要进展, 有力地推动了FeAl合金的实用化进程[1].

合金表面的成分分布与材料的表面性能密切相关. 合金表面偏析是指合金表面的成分与其体内成分不同的现象. 凡是对合金表面敏感的问题和性能, 诸如催化、腐蚀、氧化、摩擦磨损和晶体生长等都与之有关. Voges等[2]应用LEIS研究了Fe3Al(110)面在有序—无序转变温度附近时的表面偏析, 发现Al在表面富集, 而Fe在次表面富集. Eltester等[3]应用AES和LEED研究了Fe85Al15单晶合金(100)面的表面偏析和氧化, 发现Al在表面富集, 高温时表面生成Al2O3薄层, 形成(6 × 6)的超结构. 从理论上对合金表面偏析现象进行计算和预测, 不仅对深入了解这个问题具有重要意义, 而且对表面偏析现象进行实验研究具有指导作用. 从20世纪七八十年代开始人们相继提出了一些计算表面偏析的理论模型, 如基于Miedema理论[4]的热力学理论[5]、纯经验的断键模型[6]和半经验的BFS理论[7], 以及基于第一性原理的电子理论[8]等. 基于热力学计算的理论, 只能描述合金元素表面偏析的倾向, 且与实验结果偏差较大. 基于第一性原理计算的电子理论, 物理思想深刻, 但因计算过程极其繁杂而在应用上受到限制. 基于密度泛函理论, 包括了多体相互作用的半经验的嵌入原子方法(EAM)理论, 既具有较深刻的物理实质, 计算上又比第一性原理方法简单, 应用于表面偏析的理论研究比较合适. 但由于原有EAM理论模型缺乏一个统一普适的分析型形式, 通常只能针对个别的合金系统进行计算, 而无法推广应用于更多合金系统的计算. 而且已有这些研究都只局限于一些fcc结构的二元合金系统表面偏析的模拟研究, 对bcc结构的二元合金、hcp结构的二元合金以及不同结构元素组成的二元合金系统的表面偏析计算机模拟还没有人进行过系统研究. Fe为bcc金属元素, Al为fcc金属元素, 因此对Fe3Al合金表面偏析的研究具有重要的理论意义和实用价值. 本文应用改进分析型EAM理论和Monte Carlo方法研究了Fe3Al合金在不同温度下的表面偏析, 发现在不同的表面方向Al均在表面偏析, 剖面成分呈振荡分布, 与已有实验结果符合较好.

1 理论模型与计算方法

EAM模型是由Daw和Baskes根据准原子概念和密度泛函理论导出的一个半经验理论[9]. 由于原有模型参数的确定不是解析形式, 不能直接和具体的物理参数相联系, 因此只适应所处理的特定系统, 如对元素计算的参数不能推广到其合金系统, 对合金系统的计算则需要用合金特性参数进行拟合[10], 使EAM理论的应用受到很大限制, 特别是不适合用来系统地处理有关合金方面的问题. 为此, Johnson提出了分析型的EAM模型, 给出了模型参数和物理参数对应关系的解析表达式, 构筑了合金势, 使特定结构的金属及合金系统的EAM模型初步普适化[11—15]. 为了克服Johnson模型不能解决负Cauchy压元素的困难, Zhang和Hu等在Johnson的EAM模型基础上发展和改进了分析型EAM理论[16—19], 将嵌入一个原子引起的能量变化表示成:

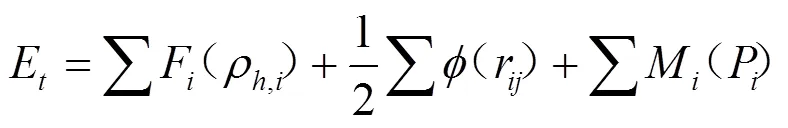
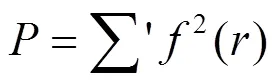
嵌入函数()和电子密度函数()分别沿用Johnson的表达式[11, 15]:

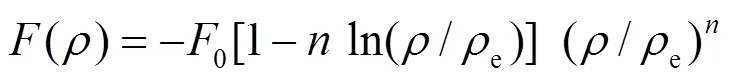
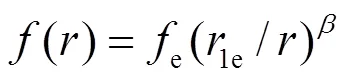
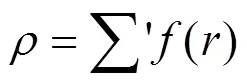
表达式中的下标e表示平衡状态, 指数β通常经验地取为6. 式(1)中的()项为修正项,为基体电子密度中原子的电子密度非球对称部分的贡献. 因此, 修正项的物理意义主要是描述原子电子密度非球对称分布所引起的系统总能量的变化. 两体势的函数形式为:

在处理势函数()时, 使用三次条样函数作为截尾函数:

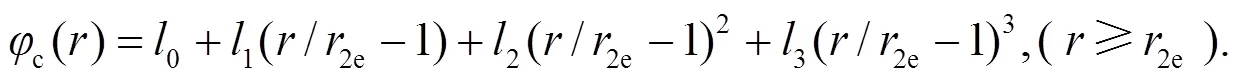
根据势函数和其一阶导数连续, 以及在特定点平滑趋于0的条件来确定截尾函数中的参数. 势函数光滑连接的条件为:

当≥c时, 势函数取0. 其中

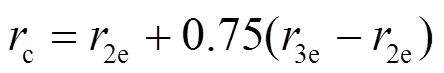
1e、2e、3e分别表示平衡时原子间最近邻、次近邻和第三近邻距离. 模型参数通过拟合纯金属的结合能c、单空位形成能1f、晶格常数, 以及弹性模量11、12和44来确定. 对于bcc元素, 可求得势函数的系数为[18]:

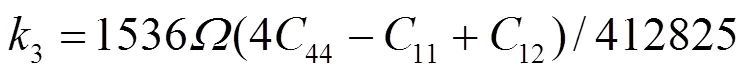
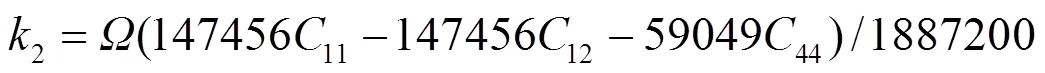
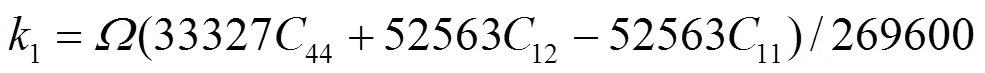
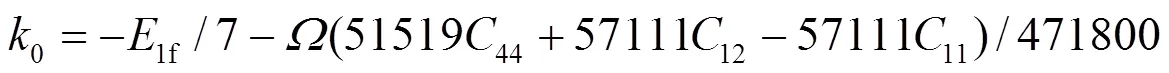
对于fcc元素, 可求得势函数的系数为[19]:

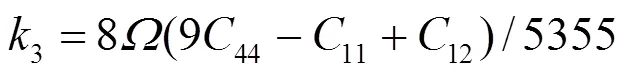
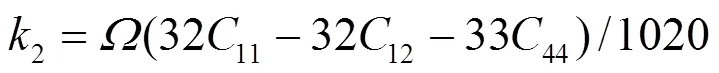
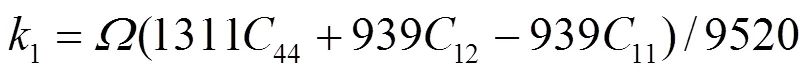
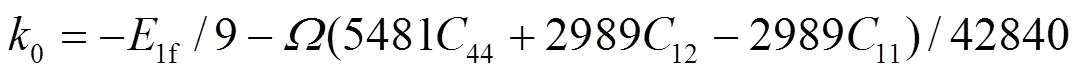
对于合金势函数本文中将采用类似于Johnson的线性叠加法[13]来表示. 这种新的合金势函数考虑了不同种类原子尺寸的影响, 具体形式为[20]:

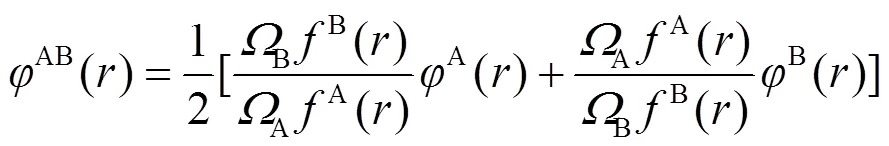
其中A、B分别指原子A和B,A、B指原子A和B的体积. 该模型的最大优点是只需要元素的各种物理特性, 即可通过所构筑的合金势计算合金的物理性能. 同时, 由于模型中的电子密度与周围原子的配位数有关, 因此模型能根据表面和体内原子配位数的不同来自动区分表面情况, 而无需另外增加其它任何条件.

在计算中系统的能量由以上建立的分析型EAM理论来计算, 对于表面偏析的计算则要应用统计学方法. Monte Carlo 方法是基于统计力学原理, 根据微观统计规律来解释可观察到的宏观物理性质. 应用Monte Carlo方法模拟表面偏析的具体方法可以参考文献[21]. 根据巨正则系综的统计规律, 从状态X到X的Markov过程的跃迁几率P为(设一个B原子取代一个A原子)[22]:

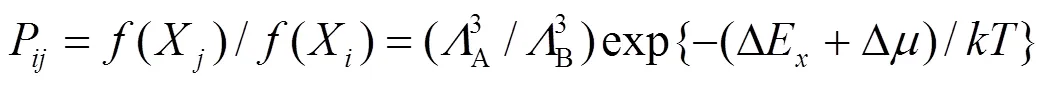
其中A、B分别是原子A、B的De Broglie波长, ∆E是状态能量的变化, ∆是两种原子的化学势之差,是Boltzmann常数,是系统的温度.

按照Metropolis算法, 在状态X向X1的演化过程中, 当系统的能量变化Δ≤0时, 接受X1状态; 当Δ＞0时, 取一个0与1之间的随机数, 若P1≥, 则接受X1状态, 否则不接受这一状态. 在Markov链经过步(足够大)以后, 对Markov链上的微观状态抽样, 计算其平均值和相应的偏差.

本文所用的计算程序是在Foiles等人的MC92程序基础上结合Zhang和Hu等人改进的分析型EAM势改编而成. 程序允许系统有3种不同的方式朝平衡态方向演化: ①原子位置可以作小的位移——模拟原子的振动与弛豫; ②整个系统的空间膨胀和收缩——模拟热膨胀效应; ③在总的原子数不变的情况下, 原子类型可以任意变化——模拟合金中原子之间通过相互扩散而达到平衡状态.

在计算机模拟过程中, 计算体成分时取8个原子层, 每层有64个原子, 空间3个方向取周期性边界条件. 计算其表面和剖面成分分布时取21个原子层, 每层同样为64个原子. 模拟过程中系统的体积和原子总数目都保持恒定, 系统的温度从700～1 400 K之间变化. 合金成分由两种元素的相对化学势∆确定. 在进行表面偏析模拟之前需要多次调整相对化学势∆来得到所要计算的合金成分. 模拟计算体成分时每个原子的平均统计步数为5 000次, 考虑到表面的影响, 在模拟计算表面时每个原子的平均统计步数增加到20 000次, 总的Monte Carlo统计步数超过2千万次.

2 结果与讨论

应用bcc和fcc金属的改进分析型EAM理论, Fe和Al元素的输入物理参数分别列于表1中, 相对应的模型参数见表2, 计算所得的势函数随距离变化的关系如图1所示.不同结构的金属元素组成的二元合金, 其无序固溶体可能存在两种与组成元素相同的结构. 对于Fe-Al合金系, 无序固溶体可能具有bcc或fcc结构类型. 假设在整个成分范围内均为bcc或fcc结构的无序固溶体, 应用改进分析型EAM模型计算的FeAl无序固溶体的形成焓如图2所示. 作为比较, 实验值[23]和Miedema理论的热力学数据[24]也一同列于图2中. 因为Fe的稳定结构为bcc结构, 所以在富Fe端fcc结构的无序固溶体的形成热为正值, 这意味着fcc结构在此成分范围里为不稳定结构. 由图2可知, 本文计算的形成焓与实验值和Miedema理论计算值都比较接近, 仅有很小的差异, 这可能是因为在计算中没有考虑系统的温度以及原子间的弛豫作用.

表1 Fe、Al元素的输入物理参数

表2 Fe、Al元素相应的EAM模型参数

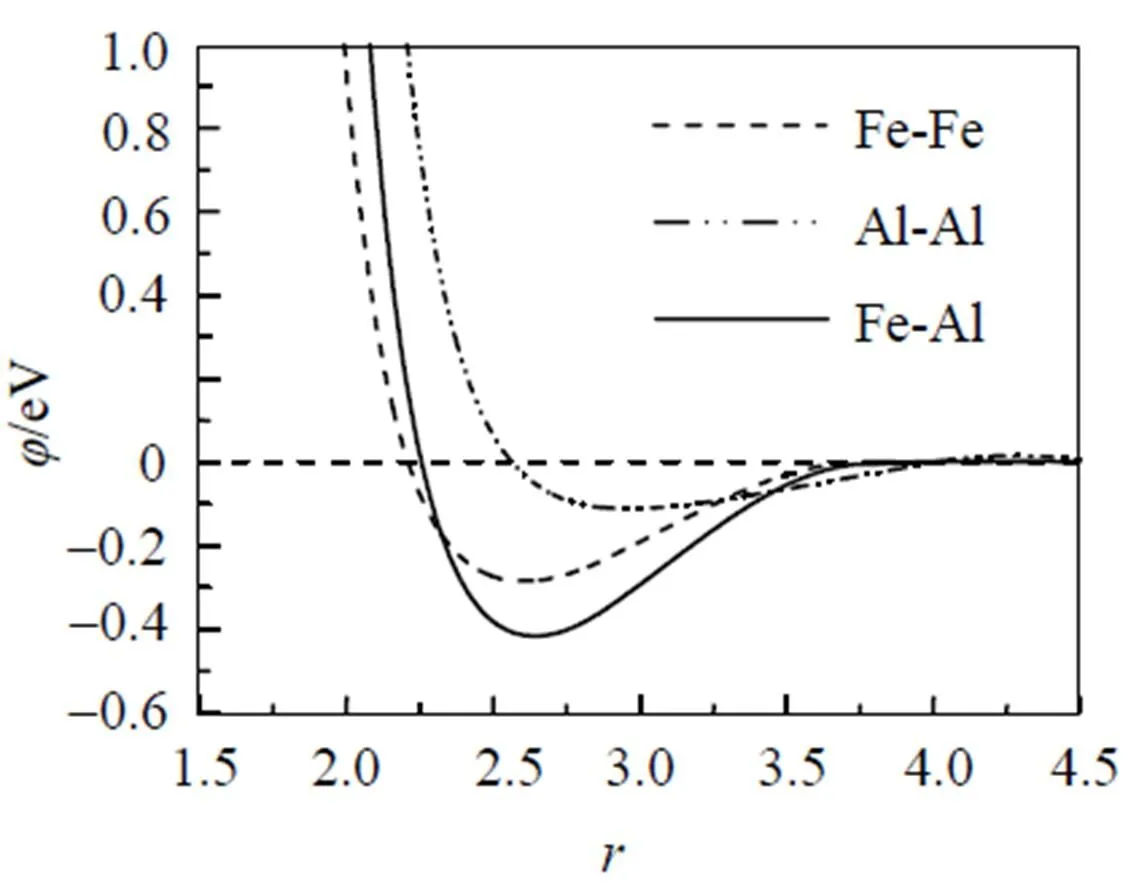
图1 Fe元素和Al元素及其合金势函数

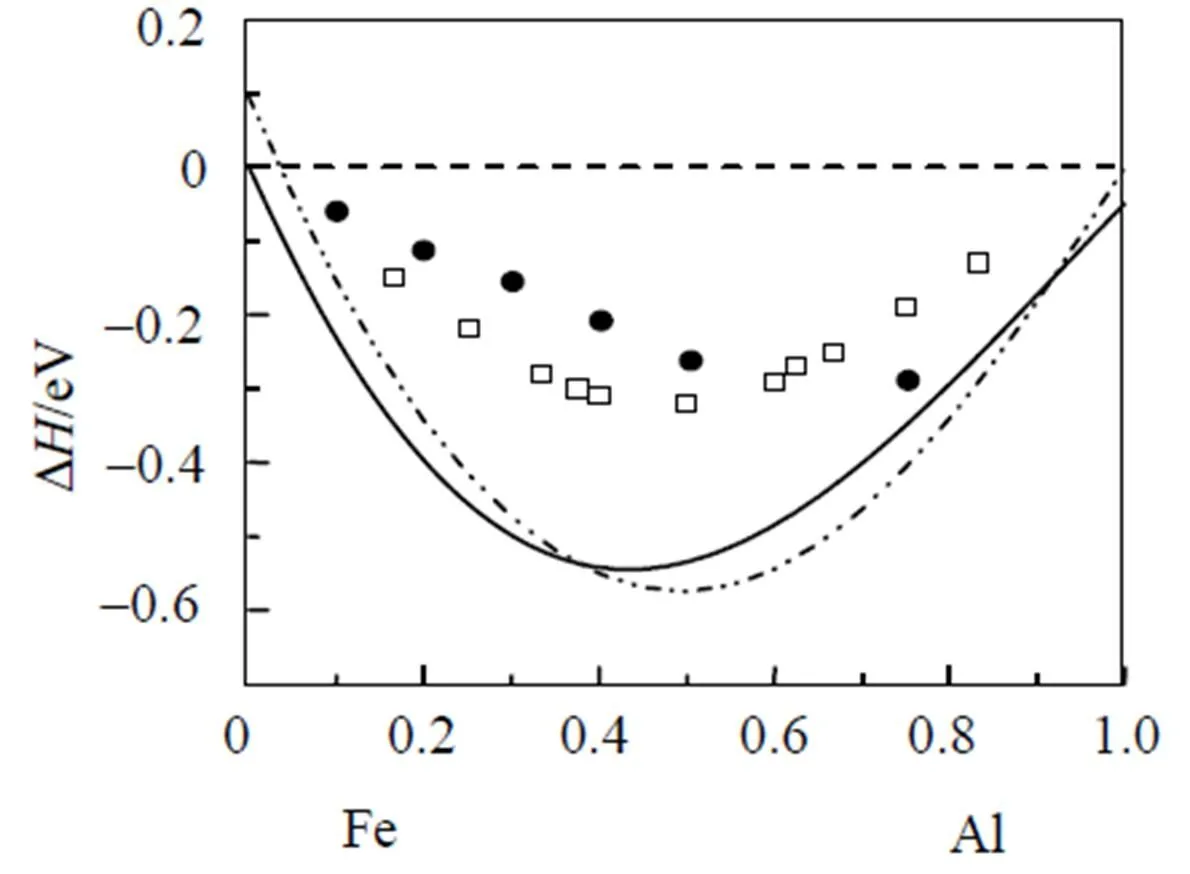
图2 Fe-Al无序固溶体的形成焓.Miedema

图3为FeAl合金系的相图[25], FeAl合金在18%～20%Al含量以下均为无序的α-Fe固溶体, 当含Al量高于18%～20%时就出现有序化. Fe3Al成分处于稳定的结构是有序的DO3结构, 但其稳定的温度随成分而异, 最高的温度c为550℃, 温度再高时稳定的结构为不完整的B2有序结构. 当Al含量达到37%以上时, 室温下也是B2稳定结构. 在23%～37%Al区间, 存在B2→DO3有序结构转变, 高于c时为B2结构. 用Monte Carlo方法与EAM模型模拟的Fe3Al(100)面成分随温度变化的偏析情况如图4所示. 图4中的虚线表示相应的合金体成分, 1和21表示外表面原子层, 2和20表示次表面层, 其余依此类推. 因为Fe3Al成分处于稳定的结构是有序的DO3结构, 在温度为800 K左右时存在DO3→B2有序结构转变, 但本文模拟的700～900 K之间的结果发现表面Al含量随温度升高而有少量增加, 次表面Fe偏析, 剖面成分振荡分布, 除此之外并没有发现其他方面的突变. B2结构为体心结构, Al原子占据体心位置. DO3结构为8个小体心结构组成的超结构, Al原子和Fe原子间隔占据体心位置, 晶体中的Fe原子与Al原子之比为3: 1. 在DO3结构的(100)面由两层原子交替堆积而成, 一层是纯Fe原子, 另一层是Fe和Al各占一半. 这与本文中模拟的(100)面的剖面分布是一致的, 只是Al在表面发生偏析. Blum等[26]应用LEED、LEIS和STM研究了Fe1-Al(= 0.03, 0.15, 0.30)合金系(100)面的聚集和有序化, 认为平衡表面的Al含量的增加是由于Al在表面的聚集和有序相互作用的结果. Meier等[27]应用定量LEED和AES研究了Fe1-Al(= 0.03, 0.15, 0.30, 0.47)合金系的(100)方向的表面, 发现平衡状态时表面总是富集Al. 由此可见本文的模拟结果与实验结果符合得很好.

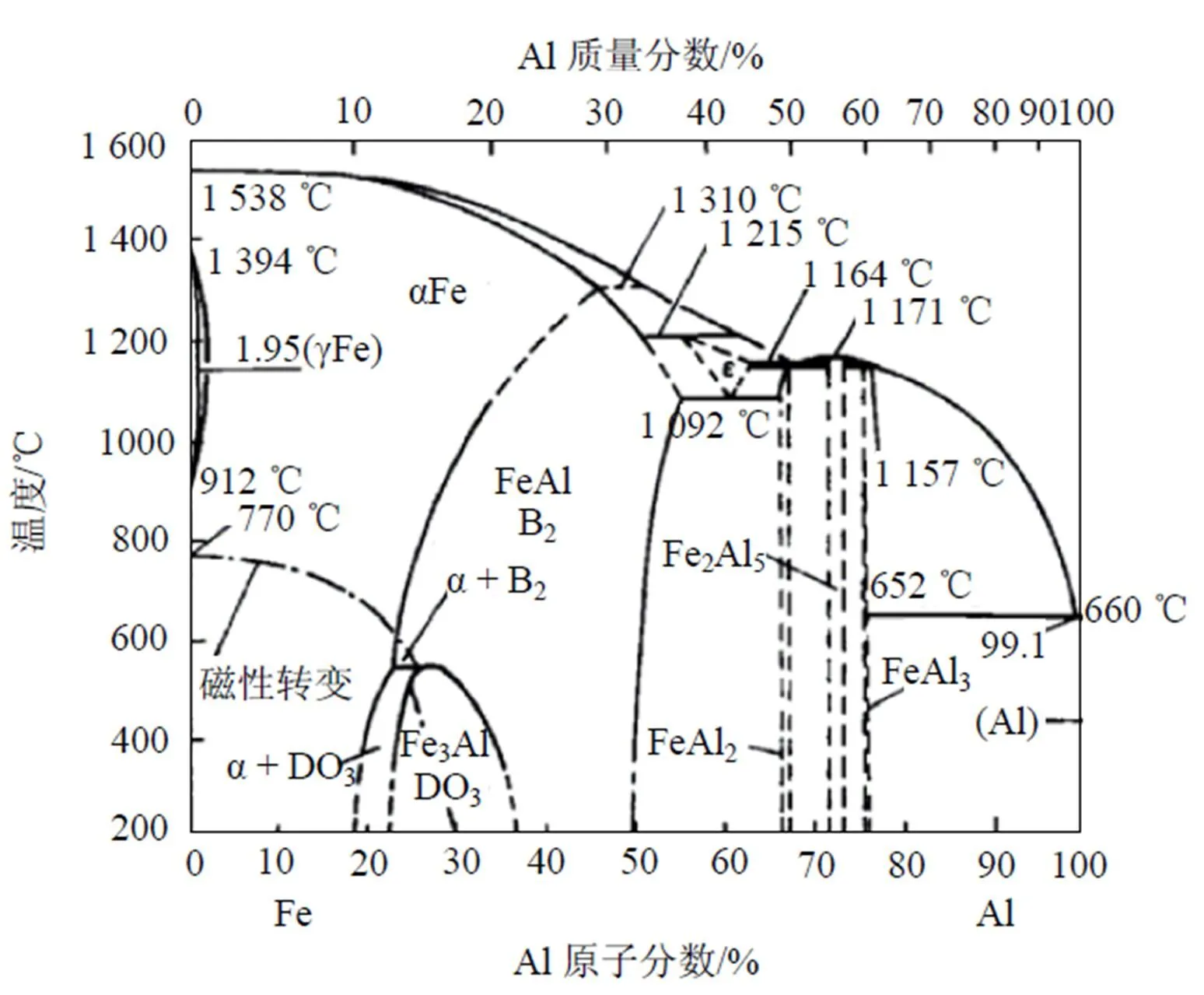
图3 FeAl 合金相图

当温度升高时, Fe3Al由DO3结构转变为不完整的B2结构时, 晶体结构中必然会出现一些结构缺陷来维持B2结构. 由于本文中的模拟方法只对成分进行统计平均, 并不能反映这些结构缺陷, 所以本文中模拟的900 K以上温度时的表面偏析, 其情形与温度较低时相差不多, 仍只能发现Al在表面偏析, 如图4(b)—4(c)所示. 当温度进一步升高到1 200 K时, 由图3可知, Fe3Al合金结构由不完整的B2结构转变为α-Fe结构, 这种结构是一种完全无序的bcc结构. 本文模拟计算的图4(c)—4(f)正好反映了这一转变过程. 在1 200 K时, 次表面的Fe原子和Al原子占位开始混乱; 1 300 K时, 合金中间的Fe原子和Al原子占位混乱得很厉害, 呈现一种无序状态; 1 350 K时合金中间部分已经是一种完全无序状态; 1 400 K时无序状态向表面方向扩展, 整个合金已经变成完全无序的α-Fe(bcc)结构, 并且在表面几层Al发生偏析.

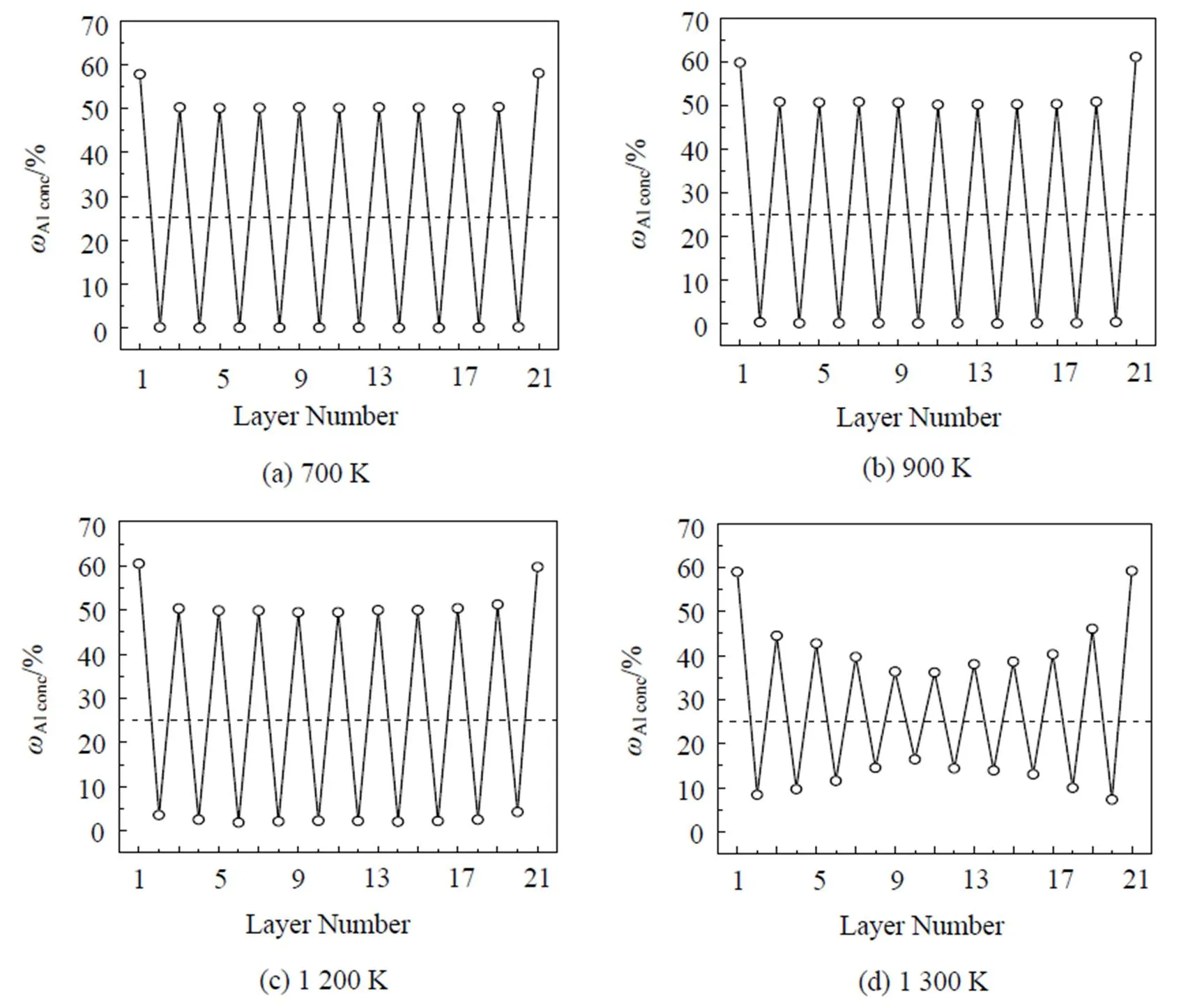
(图中1 和21 表示外表面原子层, 2 和20 表示次表面层, 其余依此类推)

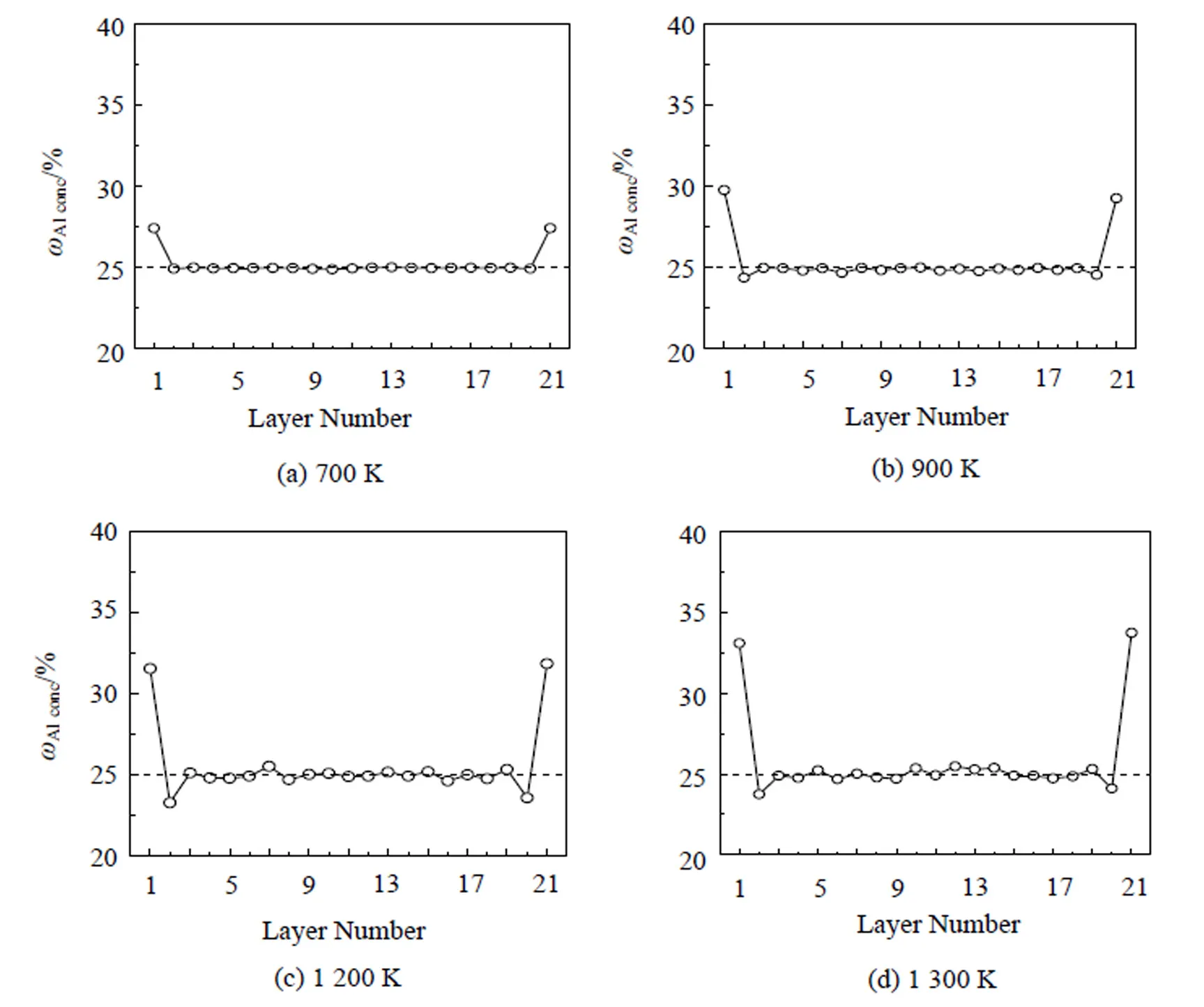
应用改进分析型EAM多体势, 结合Monte Carlo模拟的Fe3Al(110)方向的表面成分及剖面成分分布如图5所示, 在700 K时Al含量为27.4%, 800 K时为28.3%, 900 K时为29.5%, 1 300 K时稳定为33.5%左右. Hammer等[28]研究了有序FeAl合金的表面聚集现象, 发现表面形成纯Al层. Voges等[2]应用LEIS研究了Fe-29%Al合金的表面成分, 发现在室温时(110)方向的表面Al含量为43%, 在700 K时表面成分增加到94%, 在800 K以上温度时表面成分达到100%. 本文模拟结果在低温时与他们的实验结果符合较好, 但在高温时定量比较方面相差甚远. Baddorf等[29]应用X-射线衍射和反射研究了800℃时Fe-47%Al (110)面的表面, 发现表面Fe和Al的原子比为1: 2, 形成一层FeAl2层. 其表面Al的偏析量与本文计算的比较接近.

用Monte Ca -rlo模拟方法模拟的从700～1 400 K在Fe3Al合金的(110)面的成分分布, 都是Al在表面偏析, 次表面都是Fe偏析, 且随温度升高有所增加. 在温度增加的过程中发生了结构相变, 但模拟结果并没有发现任何反常. 这是因为无论是有序的DO3结构, 还是完全无序的α-Fe结构, 在(110)方向的成分分布平均值均为25%, 从平均成分分布的角度不能反映出结构的变化, 这与本文模拟的结果是吻合的.

3 结论

本文中应用Zhang和Hu等人所发展起来的改进分析型EAM理论, 结合Monte Carlo方法, 模拟计算了Fe3Al合金(100)和(110)表面的Al成分偏析情况. 模拟发现在Fe3Al (100)表面, 高温时发生有序-无序转变, 与FeAl合金相图符合得很好. 在(110)表面发现Al在表面偏析, Fe在次表面偏析, 温度较低时模拟计算结果与实验测量结果符合较好, 温度较高时模拟计算结果比实验测量结果偏低.

[1] Baker I, Munroe P R. Mechanical properties of FeAl [J]. Inter Mater Rev, 1997, 42(5): 181—205.

[2] Voges D, Taglauer E, Dosch H, et al. Surface segregation on Fe3Al near the order-disorder transition temperature [J]. Surf Sci, 1992, 269/270: 1142—1146.

[3] Elterster B, Uebing C, Viefhaus H, et al. AES and LES investigation of Al segregation and oxidation of the (100) face of Fe85Al15single crystals [J]. Fresenius Journal of Analytical chemistry, 1997, 358(1-2): 196—199.

[4] Miedema A R. Surface Segregation in Alloys of Transition Metals [J]. Z Metallk, 1978, 69: 455—461.

[5] Chelikowsky J R. Predictions for Surface Segregation in Intermetallic Alloys [J]. Surf Sci, 1984, 139: L197—203.

[6] William F L, Nason D. Binary alloy surface compositions from bulk alloy thermodynamic data [J]. Surf Sci, 1974, 45: 337—408.

[7] Bozzolo G, Ferrante J, Smith J R. Method for calculating alloy energies [J]. Phys Rev, 1992, B45(1): 493—496.

[8] Monnier R. First-principles approaches to surface segregation [J]. Phil Mag, 1997, B75(1): 67—144.

[9] Daw M S, Baskes M I. Embedded-atom method- derivation and application to impurities, surfaces, and other defects in metals [J]. Phys Rev, 1984, B29(12): 6443-6453.

[10] Foils S M, Baskes M I, Daw M S. Embedded-atom-method functions for metals Cu, Ag, Au, Ni, Pd, Pt, and their alloys [J]. Phys Rev, 1986, B33(12): 7983—7991.

[11] Johnson R A. Analytic nearest-neighbor model for fcc metals [J]. Phys Rev, 1988, B37(8): 3924—3931.

[12] Oh D J, Johnson R A. Simple embedded atom method model for fcc and hcp metals [J]. J Mater Res, 1988, 3(3): 471—478.

[13] Johnson R A. Alloy models with the embedded-atom method [J]. Phys Rev, 1989, B39(17): 12554—12559.

[14] Johnson R A, Oh D J. Analytic embedded atom method model for bcc metals [J]. J Mater Res, 1989, 4(5): 1195—1201.

[15] Johnson R A. Phase stability of fcc alloys with the embedded-atom method [J]. Phys Rev, 1990, B41(14): 9717—9720.

[16] Zhang Bangwei, Ouyang Yifang, Liao Shuzhi, et al. An analytic MEAM model for all BCC transition metals [J]. Physica, 1999, B262: 218—225.

[17] Hu Wangyu, Zhang Bangwei, Bacon D J, et al. Analytic modified embedded atom potentials for HCP [J]. J Phys: Condens Matter, 2001, 13: 1193—1213.

[18] Hu Wangyu. An analytic MEAM model and its application to intermetallic compounds [R]. Postdoctoral Research Report, Central South University of Technology, Changsha, China, 1999.

[19] Hu Wangyu, Zhang Bangwei, Shu Xiaolin, et al. Calculation of formation enthalpies and phase stability for Ru-Al alloys using an analytic embedded atom model [J]. J Alloys Compd, 1999, 287: 159—162.

[20] Hu Wangyu, Xu Huaide, Shu Xiaolin, et al. Calculation of thermodynamic properties of Mg-RE (RE = Sc, Y, Pr, Nd, Gd, Tb, Dy, Ho or Er) alloys by analytic modified embedded atom method [J]. J Phys D: Appl Phys, 2000, 33: 711—718.

[21] Deng Huiqiu, Hu Wangyu, Shu Xiaolin, et al. Monte Carlo simulation of the surface segregation of Pt-Pd and Pt-Ir alloys with an analytic embedded-atom method [J]. Surf Sci, 2002, 517: 177—185.

[22] Foiles S M. In: Surface Segregation Phenomena [M]. Dowben P A, Miller A (Eds.), Florida: CRC Press, 1990: 79.

[23] Hutgren R, Desai P D, Hawkins D T, et al. Selected values of the thermodynamic properties of binary alloys [M]. OH: American Society for Metals, 1973: 156.

[24] de Boer F R, Boom R, Mattens W C M, et al. Cohesion in Metals [M]. Amsterdam: North-Holland Publishing Company, 1988: 450.

[25] Chen Guoliang, Lin Junpin. Physical metallurgy foundation of order intermetallic compound structural materials [M]. Beijing: Metallurgical Industry Publishing House, 1999.

[26] Blum V, Hammer L, Meier W, et al. Segregation and ordering at Fe1-Al(100) surfaces: a model case for binary alloys [J]. Surf Sci, 2001, 474: 81—97.

[27] Meier W, Blum V, Hammer L, Heinz K. Equilibration of stoichiometrically distorted Fe1-Al(100) surface [J]. J Phys: Conden Matter, 2001, 13(9): 1791—1791.

[28] Hammer L, Graupner H, Blum V, et al. Segregation phenomena on surfaces of the ordered bimetallic alloy FeAl [J]. Surf Sci, 1998, 413: 69—81.

[29] Baddorf A P, Chandavarkar S S. Identification of an incommensurate FeAl2overlayer on FeAl(110) using X-ray diffraction and reflectivity [J]. Physica, 1996; B221: 141—144.

Monte Carlo simulation of the surface segregation of Fe3Al alloy

DENG HuiQiu

(Department of Applied Physics, Hunan University, Changsha 410082, China)

The surface segregation of Fe3Al alloy is simulated with our modified analytic EAM potential and Monte Carlo simulation in the present paper. The surface compositions and composition depth profiles of Fe3Al (100) and (110) faces are simulated at the temperature ranging from 700 K to 1 400 K. The results show that the topmost layers are enriched with Al, the sub-surfaces are enriched with Fe, and the Al concentration oscillates toward the bulk value. An order-disorder transition in the (100) orientation is observed at high temperatures, which is in good agreement with the Fe-Al phase diagram. The amount of Al segregation in the (110) orientation is lower than the experimental values at high temperatures. The above results are in good agreement with the available experimental data at low temperatures.

surface segregation; Fe3Al alloy; Monte Carlo simulation

TG 146.3; O 485

1672-6146(2014)02-0040-07

10.3969/j.issn.1672-6146.2014.02.009

通讯作者email: hqdeng@hnu.edu.cn.

2014-05-22

湖南省自然科学基金资助项目(03JJY3011)

(责任编校:刘刚毅)