一种分层阈值优化的语音感知小波去噪方法

曹斌芳, 彭光含, 彭元杰, 黎小琴



一种分层阈值优化的语音感知小波去噪方法

曹斌芳*, 彭光含, 彭元杰, 黎小琴

(湖南文理学院 物理与电子科学学院, 湖南 常德, 415000)

通过分析含噪语音信号的特点, 引入能够兼顾人耳听觉特性的听觉感知小波变换, 构造了新的小波阈值函数, 并对小波变换分解后的阈值进行基于微粒群算法的分层优化. 仿真实验表明, 该方法在不同信噪比条件下均具有较好的去噪性能, 语音的可懂度和听觉效果得到有效提高.

语音去噪; 听觉感知小波变换; 分层阈值; 微粒群算法

在语音通信过程中, 常常会受到环境噪声的影响, 这些噪声的存在严重影响了语音的质量, 导致接收者收到的语音信号并非纯净的原始信号. 语音信号的噪声消除技术是语音信号处理的一个重要分支, 主要是完成在保证语音可懂度的条件下, 较多地消除语音信号中的噪声成分[1]. 经过多年的发展, 研究者提出了多种语音去噪算法, 如维纳滤波方法、谱减法、子空间法、统计模型法以及小波变换法[2—4]等, 它们具有各自不同的特点, 实际应用时可以依据这些算法的难易程度及去噪效果进行选择.

语音信号是一种时变的非平稳信号, 很难用传统的维纳滤波或者卡尔曼滤波实现最优去噪, 而小波变换(Wavelet transform, WT)作为一种非常重要的非平稳信号分析工具, 它可以在很大程度上对噪声加以消除[4], 因此, 在信号处理领域获得了广泛的应用. 目前, 基于小波变化的噪声消除方法大致有以下几种: 第1种, 基于Mallat及其合作者提出的模极大值的小波去噪算法[5]; 第2种, 依据小波变换后系数之间的相关性实现小波系数的类型判别, 从而完成处理; 第3种, Donoho提出的软硬阈值去噪方法, 该方法实现简单、计算量小, 因而获得了广泛应用. 在小波阈值法进行语音信号的噪声消除时, 发现该方法不能很好地反应人耳对信号幅度以及频率的听觉特性, 因此, 文献[6—7]采用了一种听觉感知的小波变换, 建立了人类听觉系统对于声音频率的感知与实际频率的对应关系. 另外研究发现, 在小波阈值去噪法中, 不同的阈值和阈值函数都会影响到最终的去噪效果, 所以很多的研究者针对阈值和阈值函数的合理选择问题进行了大量研究. Donoho通过理论证明, 得出小波变化过程存在最优的通用阈值, 然而后续的分析和研究说明噪声和信号的小波系数具有明显不同的分布特征, 因此通用阈值很难在实际中产生很好的效果. 国内外学者提出了多种改进阈值去噪法[8—11], 本文在此基础上, 结合语音信号的特点, 构造了一个新的阈值函数, 并提出针对不同的小波分解尺度, 采用不同的阈值, 即分层阈值. 针对分层阈值的选择问题, 本文采用微粒群优化算法来确定最佳分层阈值, 最后通过实验仿真验证了该方法的有效性.

1 基于小波变化的阈值去噪法

1.1 听觉感知小波变换

人耳基底膜具有与频谱分析器相似的作用, 可将20～16 000 Hz分成24个频率群[6]. 文中引入听觉感知的小波变换进行语音信号的分解和重构, 可以很好地兼顾多分辨率的思想, 同时也使得处理后的语音信号可以在很大程度上符合人类的听觉系统特性.

定义信号()的小波变换为:

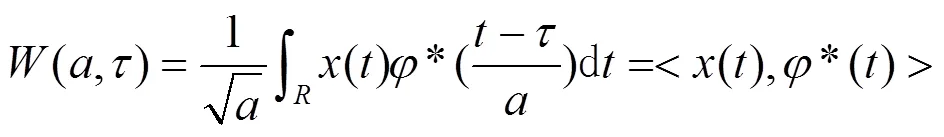
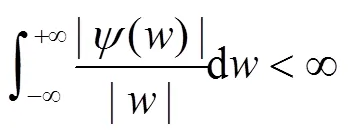
人耳的听觉系统非常复杂, 目前很难从机理结构上对它进行完全的解释. 人耳对于声音频率的理解与真实频率之间呈现一种复杂的非线性关系, 如文献[7]给出其函数表达式如下:

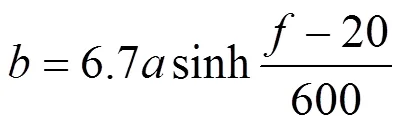
其中,代表听觉感知频率,代表线性频率.

选择小波母函数:

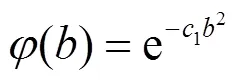
其中,1= 4ln2, 取参数(,)为(1,1-D)可得听觉感知域下的小波函数的表达式, 即:

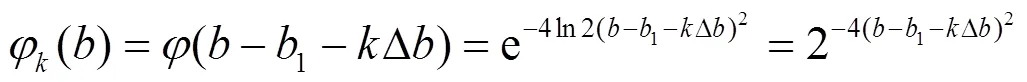
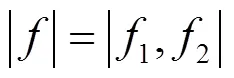
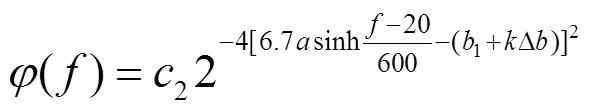
1.2 阈值函数分析

小波变换过程中阈值函数的选取是非常重要的, 它直接影响到后续对不同分解层次上小波系数的处理. 小波软、硬阈值噪声消除方法最早由Donoho等人提出[12], 其定义如下:

硬阈值:

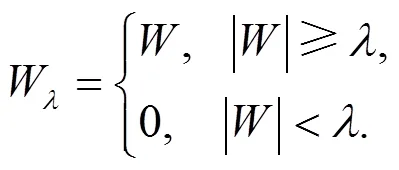
软阈值:

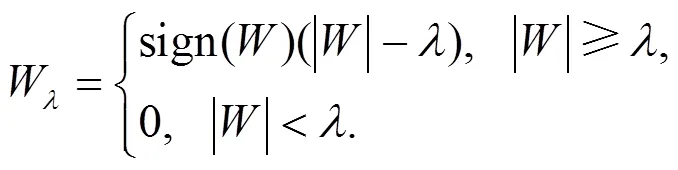
其中, sign()为符号函数, 该软、硬阈值函数在去噪方法中获得广泛应用, 也成为后续阈值去噪方法的基础.

Donoho提出的软、硬阈值函数在很多方面获得了广泛的应用, 但是研究发现它们都有一定的局限性. 比如, 硬阈值法可以较好地消除噪声, 但是由于阈值函数在连接点处存在不连续性, 进行小波去噪后, 恢复出来的信号会出现振荡现象. 相比硬阈值法, 由于软阈值方法在连接点处是连续的, 进而可以避免振荡现象的产生, 但是, 软阈值后的小波系数与真实信号的小波系数相比, 有一定的偏差, 会造成信号的逼近误差偏大.

针对软、硬阈值方法的这些缺点, 很多学者提出了改进的阈值方法, 但各种方法在小波系数小于0时都简单地设置为0, 这是不合理的. 为了既保证施加阈值后小波系数的平滑过渡, 又保证大的小波系数能够去掉噪声, 本文结合语音信号的特点构造了一种新的阈值函数, 其描述如下:

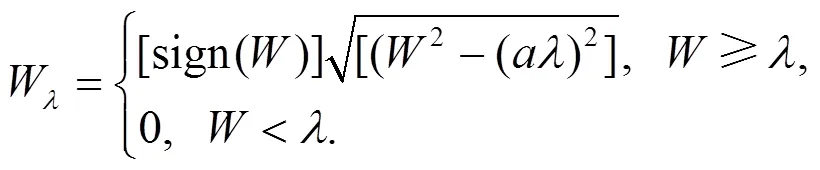
式中为0～1之间的一个参数, 即当小波系数小于阈值时, 让小波系数平滑减小到0, 大于阈值时, 小波系数的平方减去阈值平方再开方, 从而减少音乐噪声. 针对所提出的阈值函数中阈值的选取, 本文引入微粒群算法进行分层优化.

2 语音听觉感知小波变化分层阈值去噪的微粒群优化方法

2.1 微粒群算法

Kennedy和Eberhart在1995年提出了粒子群优化进化算法(Particle Swarm Optimization algorithm, PSO), 与其他进化算法相类似, PSO算法也是通过个体间的协作与竞争, 实现在复杂空间中最优解的搜索[13]. PSO算法借用了“群体”和“进化”的概念, 依据粒子的适应值大小进行变换操作, 但是与其它进化算法的不同在于, 它同时保留和利用了位置和速度信息, 从理论上将进化规划有更大可能在优化点区域内获取, PSO有更大可能更快的抵达最优解.

在PSO优化算法中, 离子从进化种群中可以提取的信息包括群体的最优位置、粒子的全局极值以及单个粒子的个体极值, 其中群体最优位置使得粒子能够快速收敛形成微粒群, 并对全局极值的邻域进行搜索, 个体自身经验最优位置保证粒子不至于过快收敛到群最优, 而陷入局部极小点, 使得粒子能够在一次迭代中对个体极值和全局极值之间的区域进行搜索.

2.2 基于PSO的感知小波语音阈值去噪方法

小波变换已经成为信号处理领域噪声消除的强有力工具, 本文在常规小波阈值去噪方法的基础上, 提出了一种分层阈值优化的语音感知小波去噪方法, 具体包括以下步骤:

Step1:利用听觉感知小波对包含噪声的语音信号进行多层分解. 设含噪语音信号表示为:

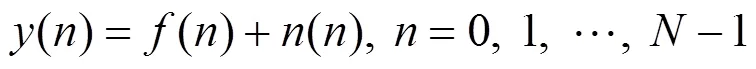
其中,为纯净语音信号,为加性噪声,为含噪语音信号,为信号的长度. 对上述含噪语音信号利用公式(1)和公式(4)进行听觉感知小波变换分解, 得到小波系数.

Step2: 初始化微粒群参数, 包括算法控制参数、粒子的速度、位置以及设置最大迭代次数.

Step3: 采用去噪信号的信噪比(Signal to Noise Ratio, SNR)作为适应值函数, 将PSO中的位置参数作为要寻优的小波阈值. 采用本文所提出的阈值函数对小波分解以后的系数进行处理, 便可以获得估计信号.

Step4:评价粒子的个体极值和种群全局极值. 具体评价包括2部分: ① 目标函数值的比较. 如果粒子当前的目标函数值小于以前获得的最优目标函数值, 则需要将当前的目标函数值作为最优的个体极值P, 否则,P保持不变. ②适应值的比较. 如果当前粒子的适应值小于全局所经历的最好位置P, 则需要将当前的适应值作为最好的位置P, 相反则P保持不变.

Step5: 更新群中粒子的速度和位置.

Step6:判断粒子的更新结束与否. 判断粒子的迭代次数是否达到了预先设定值, 是否满足精度要求, 如果满足要求, 则停止迭代, 否则重复上述Step2～Step5.

利用上述微粒群优化算法可以获得不同信噪比下的最优分层阈值POS, 再结合本文提出的阈值函数, 完成对含噪语音信号的噪声消除.

3 仿真实验和结果分析

本文采用传统的软阈值函数、硬阈值函数、文献[4]方法和本文提出的采用微粒群优化后的分层阈值方法进行去噪实验. 具体实验过程:首先从863语音库中选取语音样本, 然后设置信号的采样频率(文中为8 kHz), 最后通过改变高斯白噪声(0,W2)的噪声方差W2来达到调节语音信号输出信噪比的目的, 实验中调节范围为-10～10 dB, 间隔为5 dB. 实验用窗函数选取汉宁窗, 经过多次试验参数取0.564 2. PSO算法中的参数设置为: 种群数目25, 最大迭代次数100, 学习因子1,2均为1.370 6. 采用Morlet函数作为听觉感知小波的母小波函数, 变换尺度为22, 分解层数为3. 仿真结果如表1所示, 表1给出了4种语音去噪方法在-10～10 dB间的信噪比的改善情况.

表1 4种算法在10、5、0、-5、-10 dB处信噪比改善情况

图1给出了信噪比为-10 dB时不同去噪算法的仿真图, 其中, 图1(a)为纯净的语音信号, 图1(b)为带噪语音信号, 图1(c)、(d)、(e)、(f)分别为采用听觉感知小波变换的硬阈值法、软阈值法、文献[4]方法和本文研究所述方法去噪后的仿真图形.

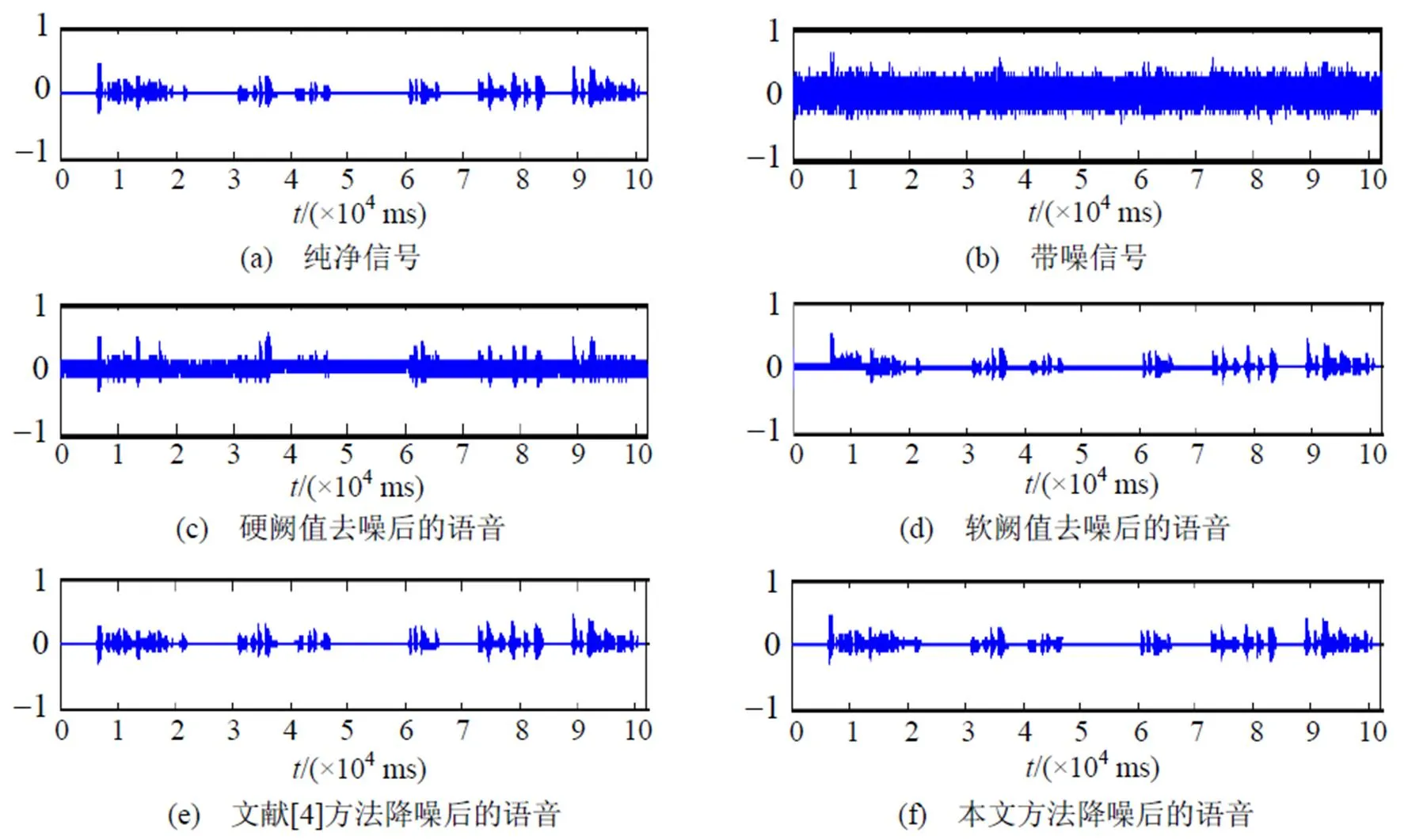
图1 采用不同阈值法去噪后的语音波形

由图1可知, 不同去噪方法的效果差别很大, 如: 硬阈值去噪法具有对噪声消除不够彻底, 而且图形中存在局部振荡和突变现象; 软阈值去噪法可以在一定程度上消除噪声, 但对语音的损害较大, 导致语音质量下降; 文献[4]的方法能够较好地去除背景噪声, 听觉效果有明显提高, 但在不同分解层次上小波层次不齐, 进而影响最终去噪效果. 本文提出的方法克服了上述问题, 对语音质量有较大的改善.

表1数据进一步说明, 随着信噪比的降低, 本文方法对噪声的抑制效果也越来越明显, 其原因主要是因为听觉感知小波变换保证了人耳对信号幅度以及频率的听觉特性, 微粒群优化阈值能够保证最优的分层阈值. 结合人耳的听觉测试, 进一步说明本文提出的分层阈值优化的语音感知小波去噪方法具有较好的听觉效果, 能够满足通信中语音信号的质量要求.

4 结束语

针对传统小波变化去噪方法存在的一些问题, 本文从小波变换后阈值函数和阈值的优化问题出发, 进行了相应的改进和优化. 本文方法兼顾了人耳对声音信号的感知特性, 构造了新的阈值函数, 并对小波变换后的阈值进行基于PSO算法的参数优化. 实验结果表明, 本文方法能有效地去除语音信号中包含的高斯白噪声, 提高峰值信噪比, 并能较好地保留语音信号的细节. 与小波硬阈值法、软阈值法、感知小波软阈值法相比, 本文方法在不同信噪比条件下均具有较好的去噪性能, 在语音波形的视觉和听觉效果2方面都有明显地改善.

[1] You C H, Rahardja S, Koh S N. Audible noise reduction in eigendomain for speech enhancement [J]. Audio Speech and Language Processing, IEEE Transactions on, 2007, 15(6): 1753—1765.

[2] 李如玮, 鲍长春. 基于小波变换的语音增强算法综述[J]. 数据采集与处理, 2009, 24(3): 362—368.

[3] Ephraim Y, Malah D. Speech enhancement using a minimum mean-square error short-time spectral amplitude estimator [J]. IEEE Trans Acoust, Speech Signal Process, 1984, 32(6): 1109—1121.

[4] Donoho D L. De-noising by soft-thresholding [J]. IEEE Trans on Information Theory, 1995, 41(3):613—627

[5] Mallat S, Hwang W L. Singularity Direction and Processing with Wavelets [J]. IEEE Trans on IT, 1992, 38(2): 617—643.

[6] Yu Shao, Chip-Hong Chang. A versatile speech enhancement system based on perceptual wavelet denoising [J]. Circuits and Systems, 2005(2): 23—26.

[7] 曹斌芳, 李建奇. 一种基于听觉特性的自适应小波语音增强方法[J]. 计算机工程与应用, 2012, 47(33): 123—125.

[8] Tao Z, Zhao H, Gu J, et al. Speech feature extraction of cochlear implants on the basis of auditory perception wavelet transform [C]. Shanghai: Audio, Language and Image Processing, 2008. ICALIP 2008. International Conference on IEEE, 2008: 80—86.

[9] Virag N. Single channel speech enhancement based on masking properties of the human auditory system [J]. Speech and Audio Processing, IEEE Transactions on, 1999, 7(2): 126—137.

[10] Hu Y, Loizou, Philipos C. Speech enhancement based on wavelet thresholding the multitaper spectrum [J]. IEEE Trans on Speech and Audio Processing, 2004, 12(1): 59—67.

[11] Lei S F, Tung Y K. Speech enhancement for nonstationary noises by wavelet packet transform and adaptive noise estimation [C]. Hongkong: International Sym. on Intelligent Signal Processing and Comm. Systems, 2005: 41—44.

[12] Donoho D L, Yu T P Y. Robust nonlinear wavelet transform based on median-interpolation [J]. Conference Record of the Thirty-First Asilomar Conference on. IEEE, 1997, 1: 75—79.

[13] Kennedy J, Eberhart R. Particle swarm optimization [J]. Proceedings of IEEE international conference on neural networks, 1995, 4(2): 1942—1948.

Speech de-noising algorithm of perception wavelet transform based on hierarchical threshold optimization

CAO BinFang, PENG GuangHan, PENG YuanJie, LI XiaoQin

(College of Physics and Electronics Science, Hunan University of Arts and Science, Changde 415000, China)

By analyzing the characteristicof noisy speech signals, audio perception wavelet transform was introduced, which considered human auditory effect. New wavelet threshold function was constructed and hierarchical optimization was performed based on particle swarm optimizationalgorithm after wavelet transform. Simulation indicated that the proposed method had a good de-noising effect under circumstances of different signal-noise-ratio(SNR) , improved speech intelligibility and auditory effect.

speech de-noising; auditory perception wavelet transform; Hierarchical threshold; particle swarm optimization

TN 912

1672-6146(2014)02-0035-05

10.3969/j.issn.1672-6146.2014.02.008

通讯作者email: cao_bf@163.com.

2014-05-06

湖南省科技计划资助项目(2010SK3052); 光电信息集成与光学制造技术湖南省重点实验室资助项目; 湖南文理学院重点学科建设项目(无线电物理).

(责任编校: 江 河)