W纠缠辅助下的熵测不准关系

倪顺利,贺 志,姚春梅



W纠缠辅助下的熵测不准关系

倪顺利,贺 志,姚春梅*

(湖南文理学院 物理与电子科学学院, 湖南 常德, 415000)

利用弱测量与反弱测量技术, 研究了基于W纠缠辅助的熵测不准关系在振幅阻尼噪声下的演化行为. 分别对单粒子和双粒子经历噪声的情况进行了模拟计算, 发现弱测量与反弱测量技术对双粒子经历噪声的纠缠恢复优于单粒子噪声情况. 在双粒子噪声情况下, 2个不对易的力学量在同一个体系中的测不准量会明显减少, 计算发现该测不准量与弱测量和反弱测量强度、阻尼衰减系数等因素有关. 阻尼衰减系数在一定的范围内, 弱测量与反弱测量技术有效地提高了W纠缠态抵御噪声的能力, 本文给出了关于不确定量更紧的束缚.

W纠缠; 弱测量; 熵测不准关系; 振幅阻尼通道

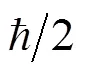
1 单粒子经历AD噪声通道熵的演化情况

设体系中有3个qubit处在W态时, 体系的波函数能表示成:

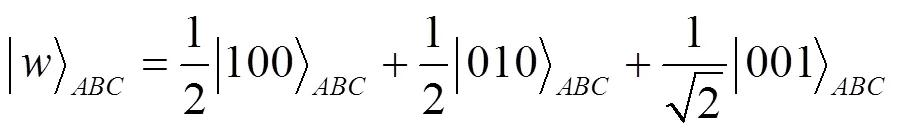
弱测量:

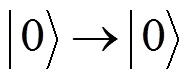
AD噪声通道(振幅阻尼噪声通道):

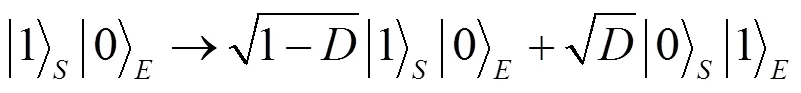
反弱测量:

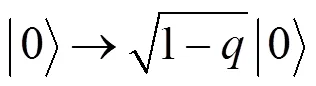
让粒子依次经过弱测量、振幅阻尼噪声通道、反弱测量, 计算得到:

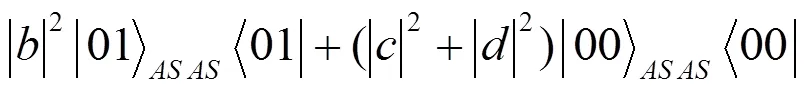
其中:

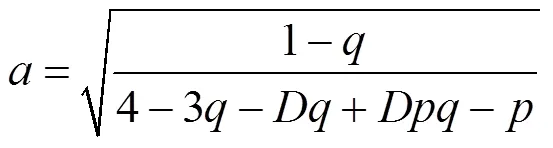
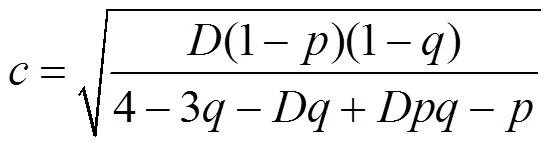
等价地, 可将写成密度矩阵的形式为:

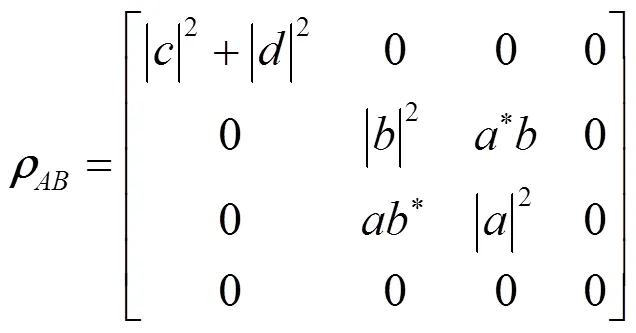
()为的von Neumann entropy, 通过计算得到:

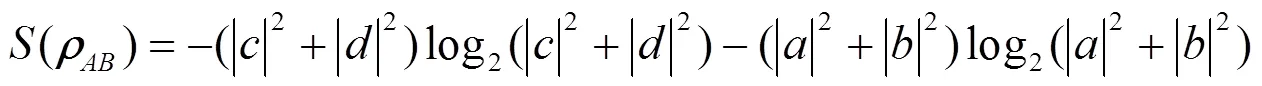
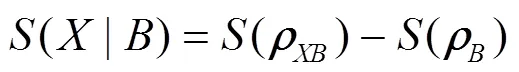
令()为的冯若依曼熵, 计算得到:

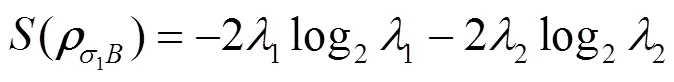
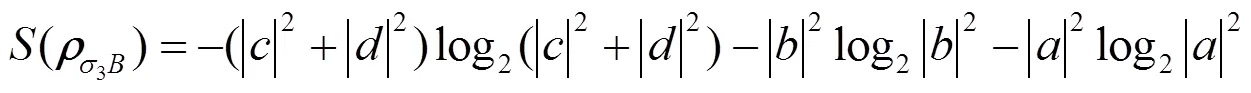
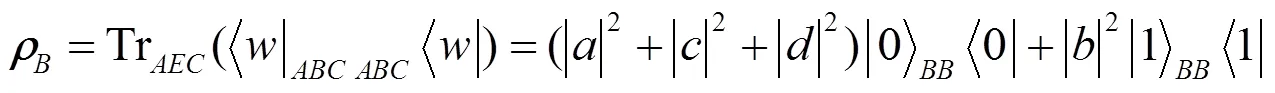
()为的冯若依曼熵:

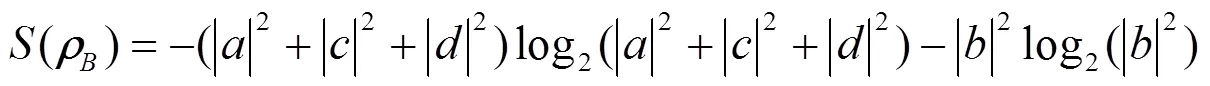
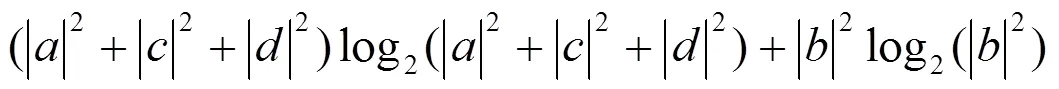
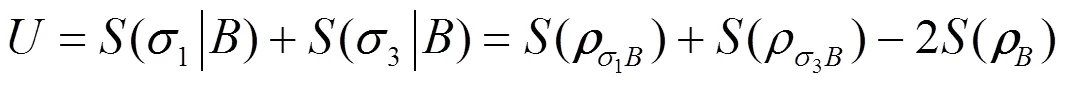
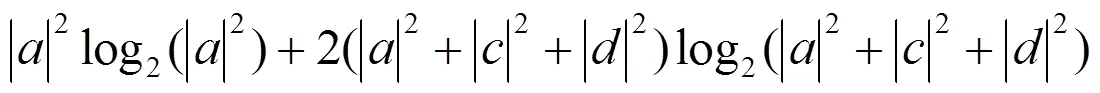
文中和U是关于弱测量与反弱测量强度及AD通道系数的函数, 将通道系数转化为振幅阻尼噪声系数,与的关系为= 1-e-,为振幅阻尼衰减系数.

从图1以及通过程序筛选可知其最大纠缠是在= 0.93,= 0.99取得的.

图2为没有用弱测量和反弱测量, 即= 0,= 0时测不准量(用、U表示)随阻尼衰减系数的变化曲线. 从图2发现, 在较小的一段范围内测不准量随的增加而增加, 并且和U接近程度越好. 当增大到某一值时, 测不准量、U达到一个稳定值.

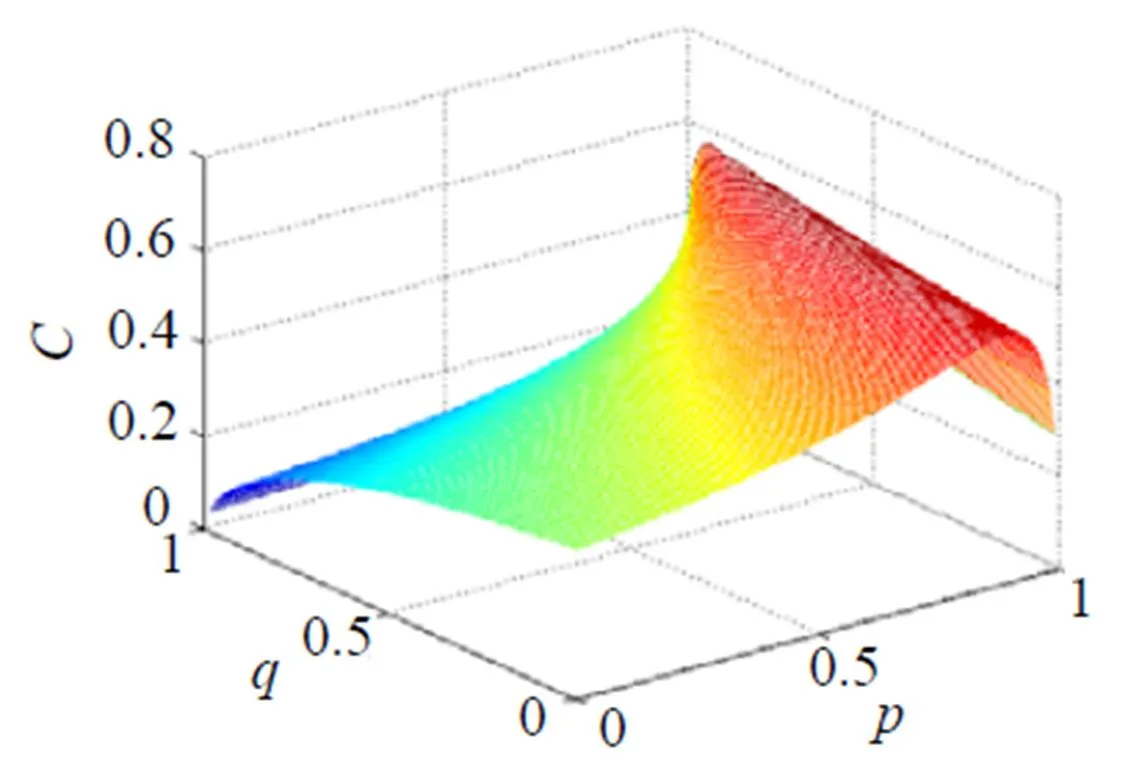
图1 rAB纠缠度随弱测量和反弱测量强度的变化曲线

图3为利用弱测量和反弱测量当= 0.93,= 0.99(最大纠缠)时, 测不准量(、U)随阻尼衰减系数的变化曲线. 从图3发现, 在趋近于0时,U相比= 0,= 0时要小, 而有所增加. 测不准量的变化趋势与= 0,= 0的情况相当.

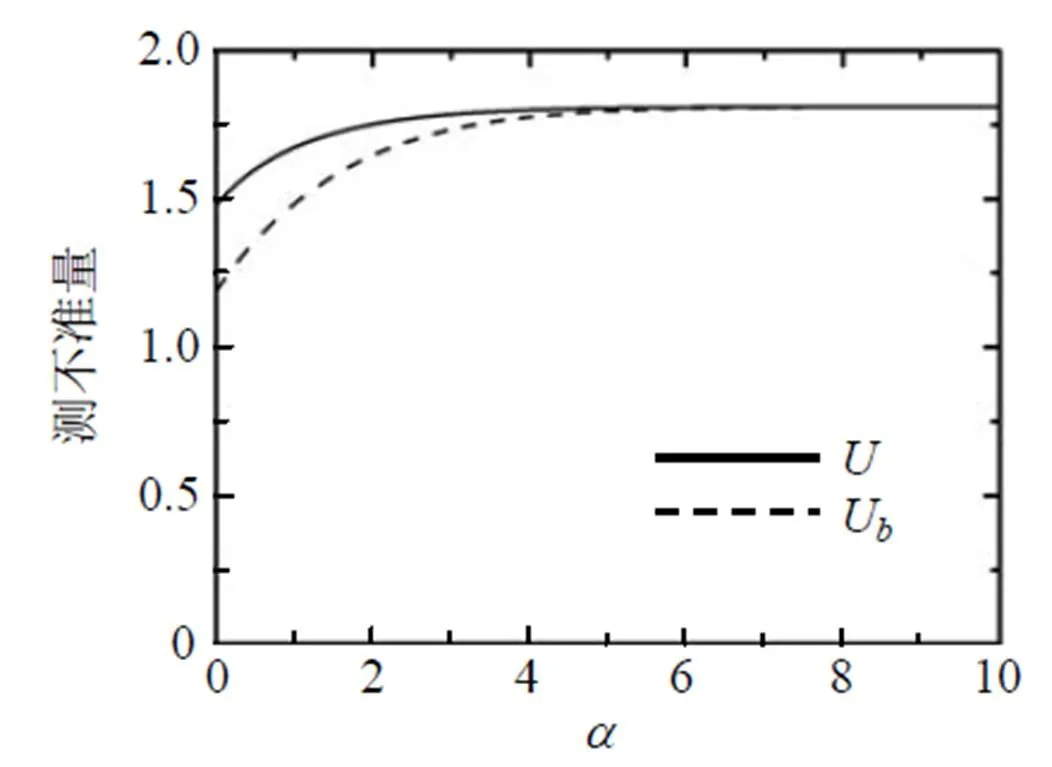
图2 p = 0, q = 0 时, 测不准量随阻尼衰减系数的变化

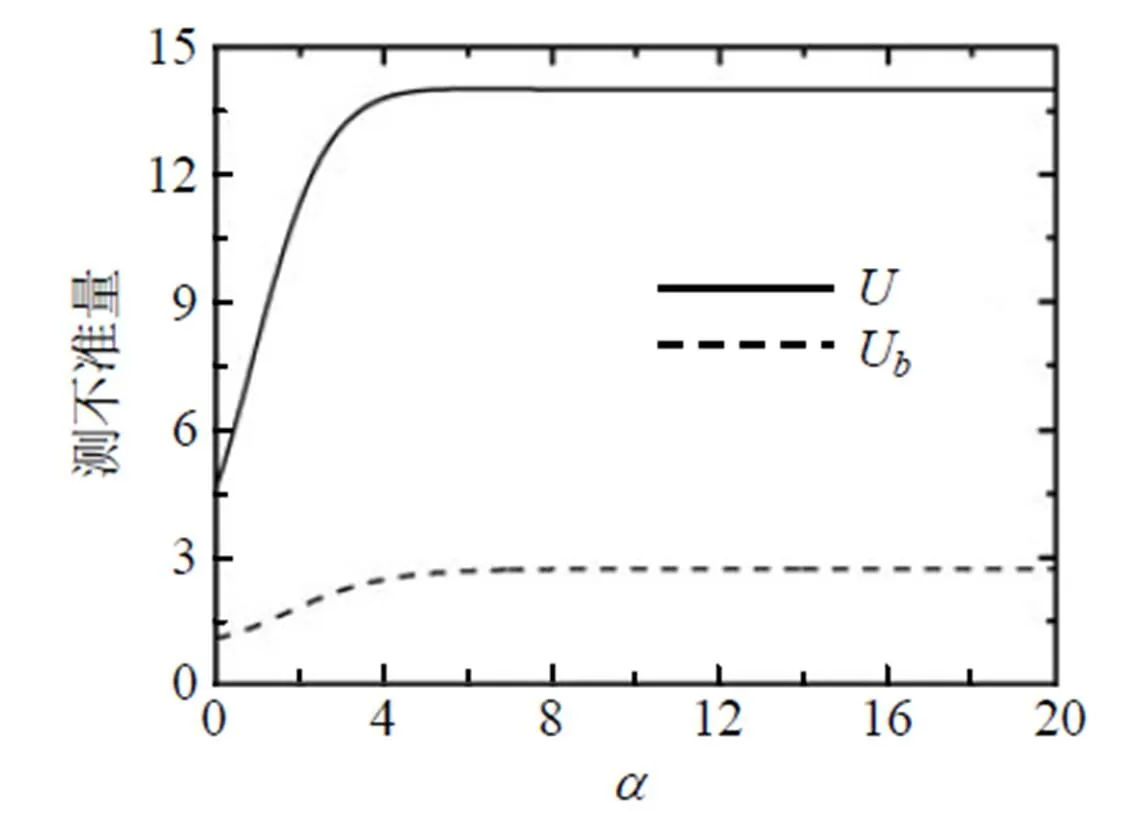
图3 p = 0.93, q = 0.99 时, 测不准量随阻尼衰减系数的变化

图4为利用弱测量和反弱测量= 0.5,= 0.9时测不准量(、U)随阻尼衰减系数的变化曲线. 从图4可发现, 由于、的取值变化, 测不准量和U有所下降.

图5为=0.5,= 0.4时测不准量(、U)随阻尼衰减系数的变化曲线. 从图4可知,很小时, 测不准量接近程度要优于=0,= 0时的测不准量的接近程度, 并且相应的测不准量有所下降.

从以上分析可知, 在单粒子情况下, 使用弱测量与反弱测量技术较不使用相比熵测不准关系吻合得要好, 并且相应的测不准量也会降低; 与两体纠缠经历振幅阻尼噪声通道相比, 相应的测不准量有所降低, 说明使用弱测量与反弱测量提高了W纠缠态抵御噪声的能力.

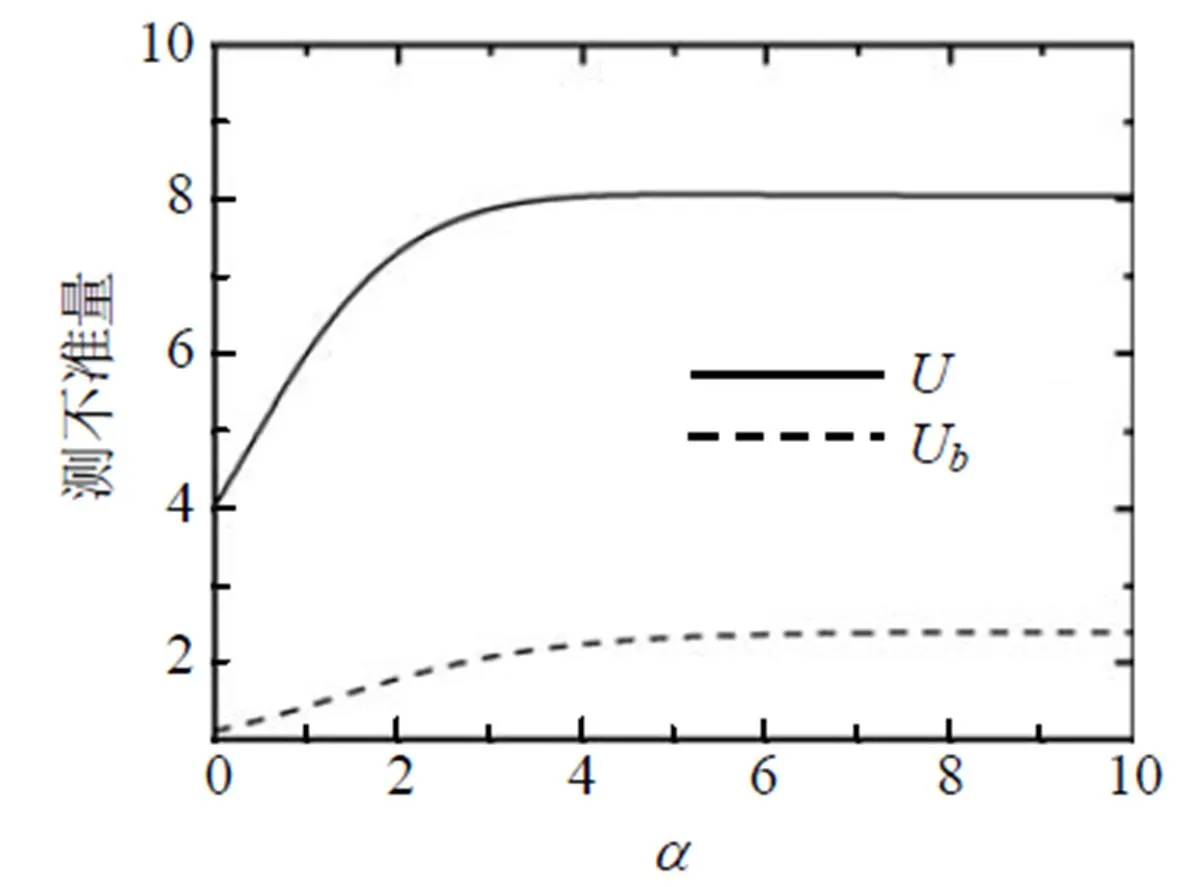
图4 p = 0.5, q = 0.9 时, 测不准量随阻尼衰减系数的变化

2 两粒子经历AD噪声通道熵的演化情况

设体系中有3个qubit处在W态时, 体系的波函数能表示成(1)式的开式. 弱测量为:

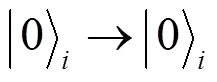
双粒子经历AD噪声通道(振幅阻尼噪声通道)与单粒子情况计算公式相同, 单考虑到通道对2个粒子的作用可能不一样, 所以设定了1和2系数. 反弱测量:

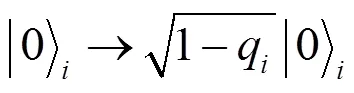
让、粒子依次经过弱测量、振幅阻尼噪声通道、反弱测量, 计算得到:

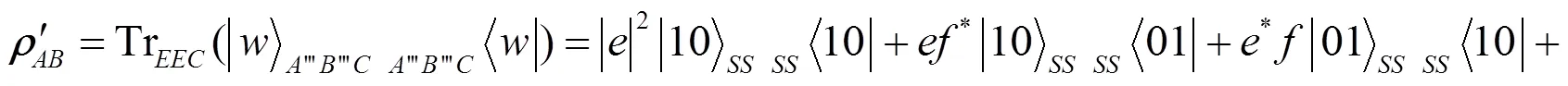
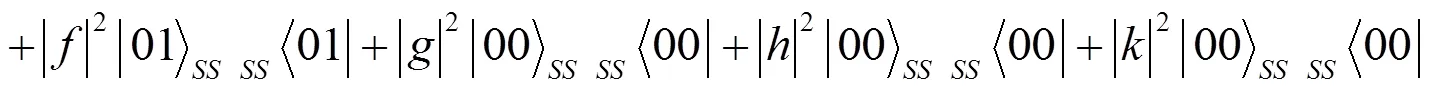
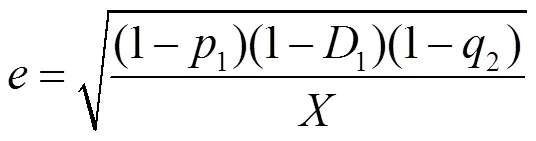
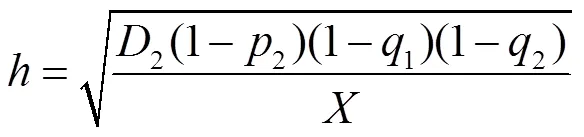
等价地, 可将它写成密度矩阵的形式为:

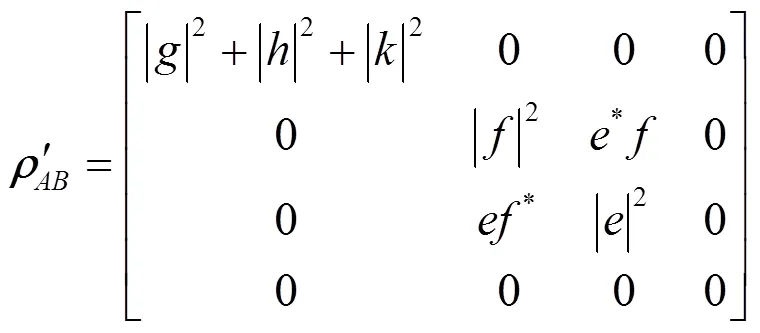
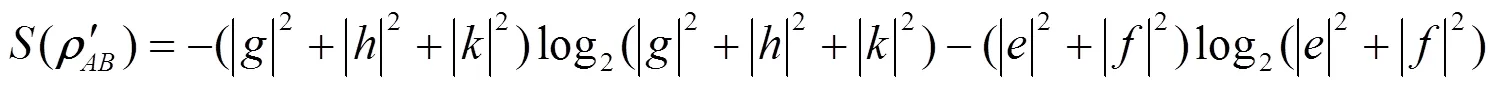
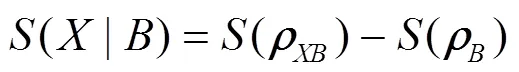
令()为的冯若依曼熵, 计算得到:

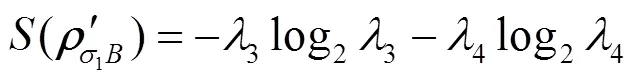
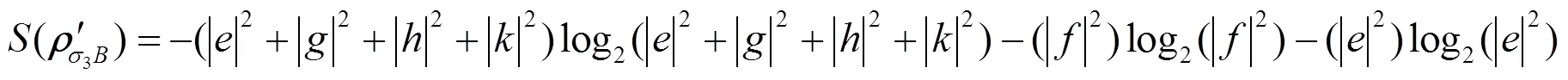
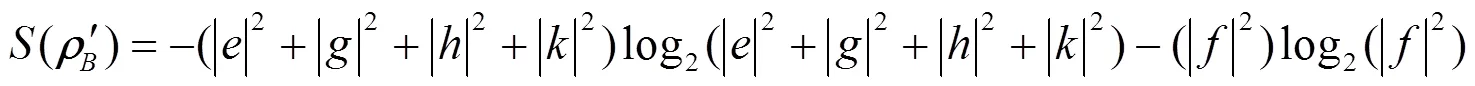
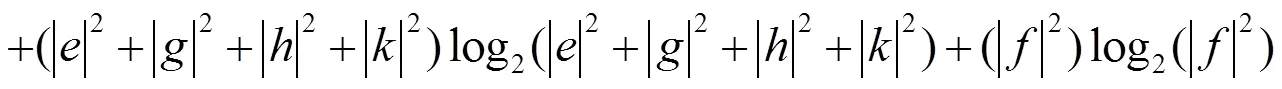
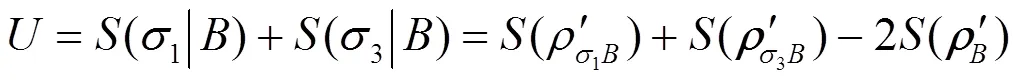
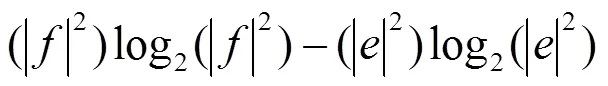
密度算子rAB为X型矩阵, 它的纠缠度是关于弱测量与反弱测量的函数, 其函数关系用matlab绘出. 从图6及通过程序筛选其最大纠缠在p1= p2 = 0.01, q1 = q1 = 0.99取得.

图7为没有用弱测量和反弱测量, 即1=2= 0,1=1= 0时, 测不准量(、U)随阻尼衰减系数的变化曲线. 从图7可知, 在较小的一段范围内测不准量随的增加而增加, 并且和U随减小, 其接近程度越好; 当增大到某一值时,、U逐渐减小.

图8为利用弱测量和反弱测量1=2= 0.01,1=1=0.99(最大纠缠)时, 测不准量(、U)随阻尼衰减系数的变化曲线. 从图8可知, 现在趋近于0时,U比在1=2= 0,1=1= 0时要小得多, 而有所增加; 随着阻尼衰减系数的增加测不准量、U趋于稳定.

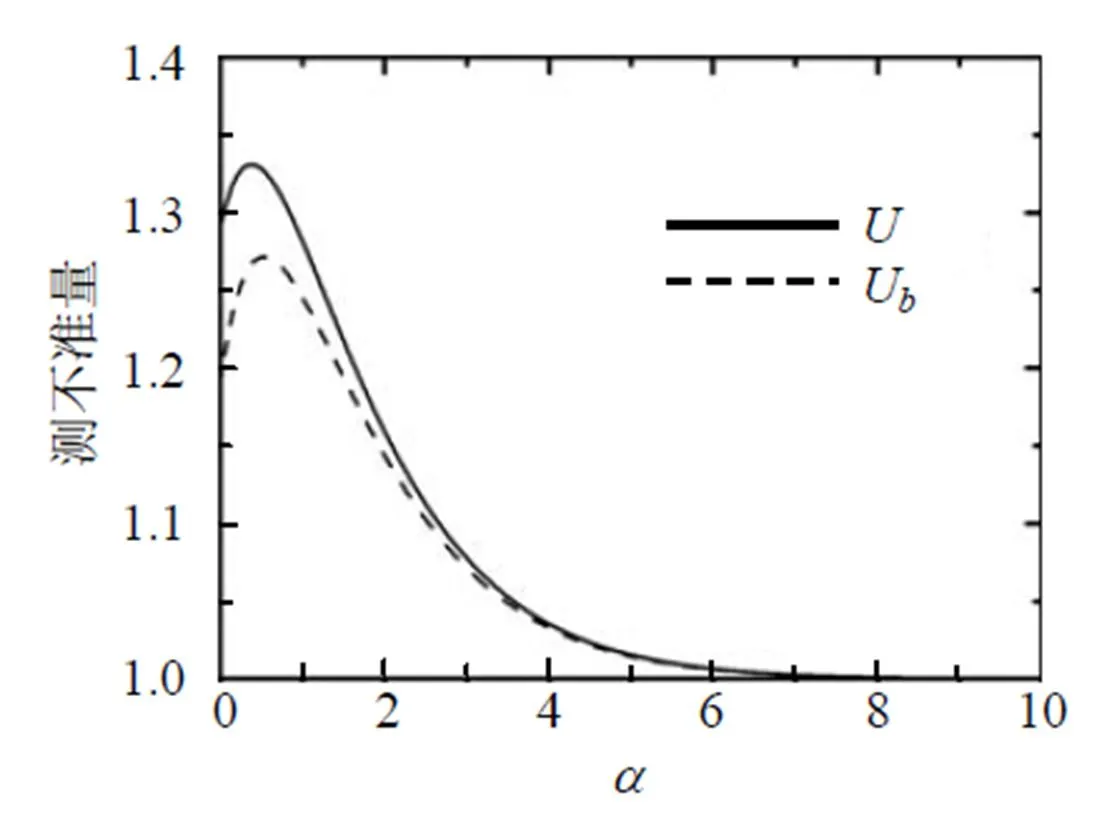
图7 没有用弱测量和反弱测量(p1 = p2 = 0, q1 = q2 = 0)时, 测不准量随阻尼衰减系数的变化

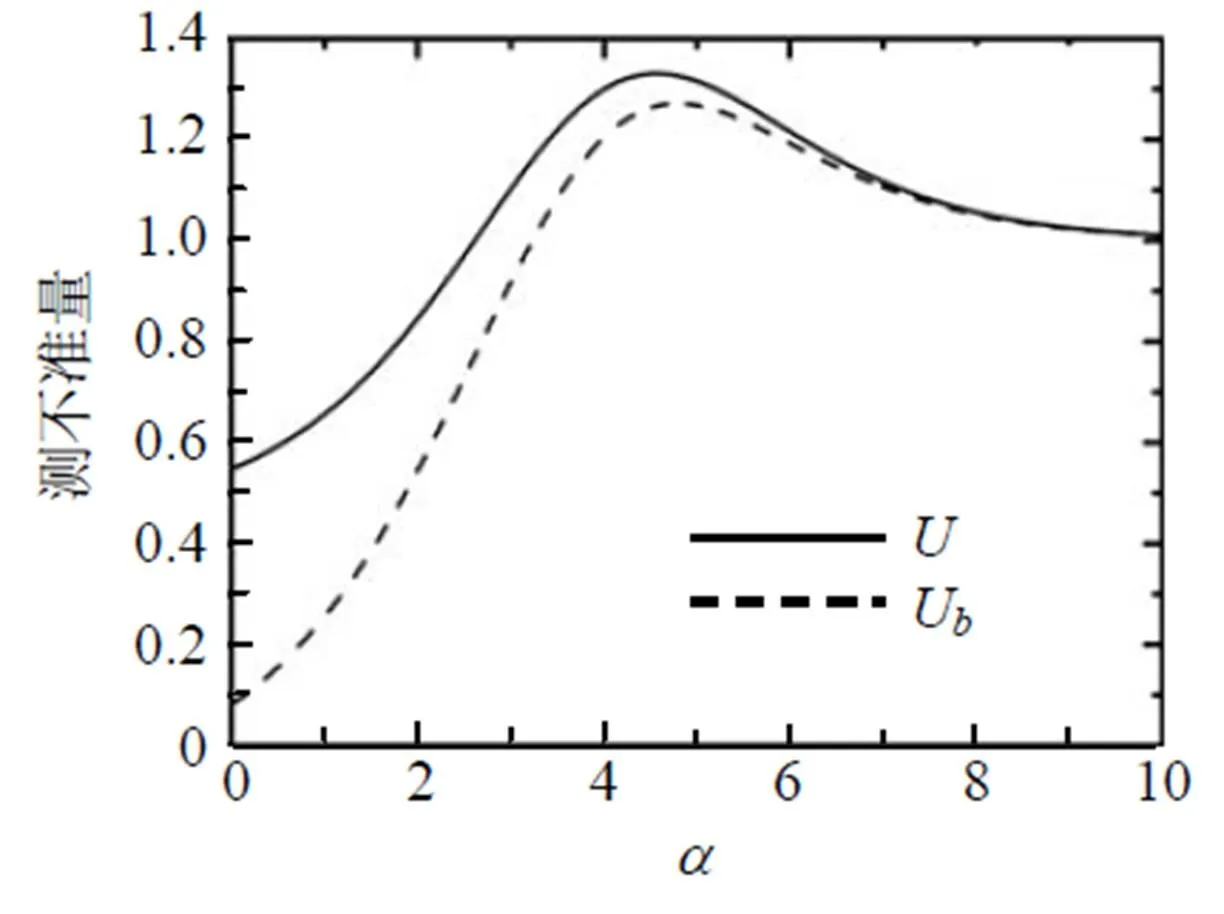
图8 利用弱测量和反弱测量p1 =p2 = 0.01, q1 = q2 = 0.99(最大纠缠)时, 测不准量随阻尼衰减系数的变化

图9为利用弱测量和反弱测量1=2= 0.99,1=2=0.01时, 测不准量(、U)随阻尼衰减系数的变化曲线. 从图9可知,1、2、1、2取其它值时, 测不准量和U有所下降, 并且测不准量接近程度更好, 相应的熵测不准关系更吻合.

从以上分析可知, 使用了弱测量与反弱测量技术之后, 熵测不准关系吻合得更好, 并且相应的测不准量也会降低; 与单粒子的情况相比, 双粒子经历振幅阻尼噪声的纠缠恢复要优于单粒子; 与两体纠缠的情况相比, W纠缠态经历振幅阻尼噪声的纠缠恢复要优于两体纠缠. 以上说明双粒子经历噪声时使用弱测量与反弱测量提高了W纠缠态抵御噪声的能力.

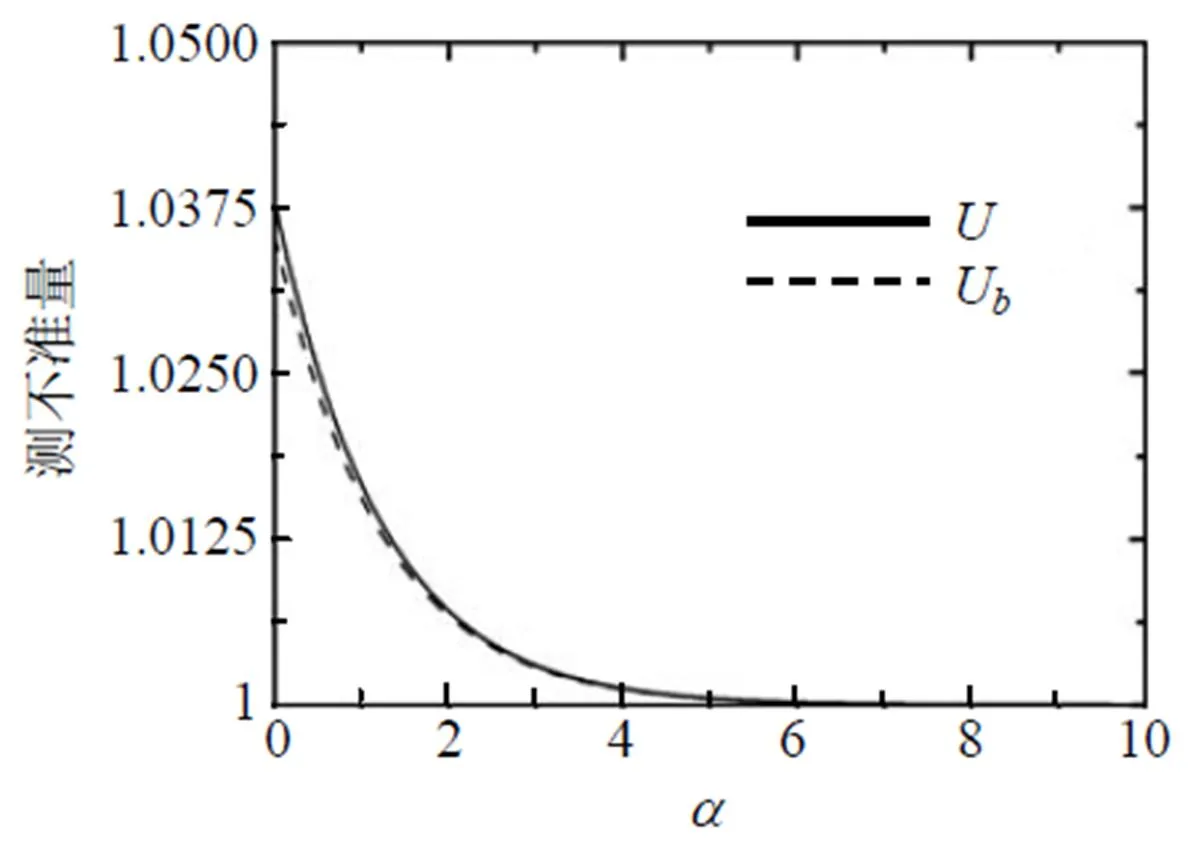
图9 弱测量和反弱测量p1= p2 = 0.99, q1 = q2 = 0.01时, 测不准量随阻尼衰减系数的变化

3 结论

在W纠缠经历振幅阻尼噪声的熵测不准关系的研究中, 本文采取了对单粒子和双粒子分别经历振幅阻尼噪声通道, 对比使用与不使用弱测量与反弱测量技术时的测不准量的变化关系, 发现弱测量与反弱测量技术会提高W纠缠态抵御噪声的能力, 并且, W纠缠态在双粒子经历振幅阻尼噪声通道使用弱测量与反弱测量技术的纠缠恢复要优于两体纠缠的情况. 该研究结果对W纠缠经历幺正噪声通道有借鉴意义.

[1] 周世勋. 量子力学教程[M]. 2版. 北京: 高等教育出版社, 2009: 79—81.

[2] 李承祖. 量子纠缠在量子信息处理中的应用[M]. 长沙: 国防科技大学出版社, 2000: 77—99.

[3] 姚春梅, 顾永建, 聂建军, 等. 量子纠缠在量子信息处理中的应用[M]. 长沙: 中南大学出版社, 2010: 2—20.

[4] Xu Z Y, Yang W L, Feng M. Quantum-memory-assisted entropic uncertainty principle under noise [J]. Phys Rev A, 2012, 86: 012113.

[5] Berta M, Christandl M, Colbeck R, et al. The uncertainty principle in the presence of quantum memory [J]. Nature Physics, 2010, 6: 659–662.

[6] Winter A.Quantum information: Coping with uncertainty [J]. Nature Physics, 2010, 6: 640–641.

[7] Pati A K, Wilde M M, Usha Devi A R, et al. Quantum discord and classical correlation can tighten the uncertainty principle in the presence of quantum memory [J]. Phys Rev A, 2012, 86: 042105.

[8] Prabhu R, Pati A K, Sen De A, et al. Conditions for monogamy of quantum correlations: Greenberger-Horne-Zeilinger versus W states [J]. Phys Rev A, 2012, 85: 040102.

[9] Kim Y S, Lee J C, Kwon O, et al. Protecting entanglement from decoherence using weak measurement and quantum measurement reversal [J]. Nature Physics, 2012, 8: 117–120.

[10] Agrawal P, Pati A. Perfect teleportation and superdense coding with W states [J]. Phys Rev A, 2006, 74: 062320.

[11] Li C F, Xu J S, Xu X Y, et al. Experimental investigation of the entanglement-assisted entropic uncertainty principle [J]. Nature Physics, 2011, 7: 752–756.

[12] Yao C M, Ma Z H, Chen Z H, et al. Robust tripartite-to-bipartite entanglement localization by weak measurements and reversal [J]. Phys Rev A, 2012, 86: 022312.

[13] Renes J M, Boileau J C. Conjectured Strong Complementary Information Tradeoff [J]. Phys Rev Lett, 2009, 103: 020402.

[14] Yu T, Eberly J H. Sudden Death of Entanglement: Classical Noise Effects [J]. Phys Rev Lett, 2004, 93: 140404.

[15] Tomamichel M, Renner R. Uncertainty relation for smooth entropies [J]. Phys Rev Lett, 2011, 106: 110506.

[16] Streltsov A, Kampermann A, Bruss D. Behavior of Quantum Correlations under Local Noise [J]. Phys Rev Lett, 2011, 107: 170502.

[17] Mazzola L, Piilo J, Maniscalco S. Sudden Transition between Classical and Quantum Decoherence [J]. Phys Rev Lett, 2010, 104: 200401.

Entropic uncertainty principle with W state-assisted

NI ShunLi, HE Zhi, YAO ChunMei

(College of Physics and Electronics, Hunan University of Arts and Science, Changde 415000, China )

By the weak quantum measurement and quantum measurement reversal, the entropic uncertainty principle with W state-assisted via amplitude-damping channel noise was studied and the situations of single-particle and two-particle via the noises respectively were calculated. The results show that the capability of entanglement recovery of two-particle through the noises was superior to that of single-particle by using of the technology of weak quantum measurement and it ws reversal. Furthermore, the uncertainties about the outcomes of two incompatible measurements on a particle would reduce obviously with the strengths of weak measurement and quantum measurement reversal, the damping rate etc.. For a certain values of the damping rate, a lower bound on the uncertainties was put forward, which depends on the amount of entanglement between the particle and the quantum memory.

W state; weak measurements; entropic uncertainty principle; amplitude-damping channel

O 431.2

1672-6146(2014)02-0007-06

10.3969/j.issn.1672-6146.2014.02.002

通讯作者email: yyccmei@sina.com.

email: 854815310@qq.com.

2014-05-08

光电信息集成与光学制造技术湖南省重点实验室资助项目; 科技厅计划项目(No 2010FJ3147); 湖南文理学院重点学科光学建设项目.

(责任编校: 江 河)