基于Matlab/Simulink的天线系统自适应滤波器的仿真实现

胡开宇，艾力·玉苏甫，刘 奇

(1.中国科学院新疆天文台，新疆 乌鲁木齐 830011；2.中国科学院大学，北京 100049)

基于Matlab/Simulink的天线系统自适应滤波器的仿真实现

胡开宇1，2，艾力·玉苏甫1，刘 奇1

(1.中国科学院新疆天文台，新疆 乌鲁木齐 830011；2.中国科学院大学，北京 100049)

为了使天线系统接收和显示的信号更清晰，达到消除系统噪声和电磁干扰的目的，针对中国科学院新疆天文台南山观测基地对射电天文观测和深空探测(探月工程和火星探测)的特殊要求，利用Matlab/Simulink强大的数值计算与仿真功能实现了一种依据自适应方法滤除噪声的滤波器。首先选择脉冲星1910＋0728和1913－0440的观测信号为滤波参考信号。在Matlab上通过编写M文件设计了滤波算法并有效滤除了噪声。然后运用Simulink进行建模仿真，通过不断改变系统阶数与步长找到了滤波效果最好的自适应滤波器，确定了其最优参数为8阶，迭代步长为0.005。实验表明在这种阶数和步长下，滤波器能在保证快速滤波的前提下有效地还原接收信号的轮廓，将偏差降到最小。仿真最终结果表明自适应滤波器滤波效果良好，实用性强，满足了射电天文观测和探月的需求。

天线；自适应滤波器；脉冲星；仿真

CN53－1189/P ISSN1672－7673

自适应滤波器是近几十年发展起来的信号处理理论的一个新的分支。它的研究对象是可以调整自身参数的系统，即可以通过自身与外界环境的接触来改变自身对信号处理的性能，在输入过程的统计特性未知或是输入过程的统计特性变换时，它能够调整自己的参数，达到使系统误差降到最小的目的。随着人们在该领域的研究深入，自适应信号处理的理论和技术日趋完善，其应用领域也越来越广，目前在射电天文领域，国外很多天文台已经开始采用这种新的滤波方法消除无线电干扰对天文观测带来的影响[1]。

1 自适应滤波器的结构

自适应滤波技术是一种能调节自身传输特性以达到最优化目的的维纳滤波器[2－3]，因其不需要输入信号的先验知识，因此得到了广泛的应用。自适应滤波，是利用前一时刻获得的滤波器参数的结果，自动调节当前时刻的滤波器参数，以适应信号或噪声未知的或随时间变化的统计特性，从而实现最优滤波。自适应滤波器实质上是一种能调节自身传输特性以达到最优的维纳滤波器。自适应滤波器不需要输入信号的先验知识，计算量小，特别适用于实时处理。图1给出了天线自适应滤波器的工作原理图和新疆天文台南山基地的数字滤波器实物图。

图中，x为输入信号；y为输出信号；d为参考信号；e是d和y的误差信号。自适应滤波器的滤波器系数受到误差信号e控制，根据e的值和自适应算法自动调整，用以达到滤除y中噪声的目的，并将滤除噪声后的信号传输到显示系统中。一个自适应滤波器的完整规范由3项组成:(1)应用，主要应用在回波消除、色散信道的均衡、系统辨识、信号增强、自适应波束形成、噪声消除一级控制等领域；(2)结构，有两种结构形式，有限长冲击响应(FIR)滤波器和无限长冲击响应(IIR)滤波器；(3)算法，常用的自适应算法有迫零算法、最陡下降算法、LMS算法、RLS算法以及各种盲均衡算法等[4]。应用最广泛的是LMS算法。

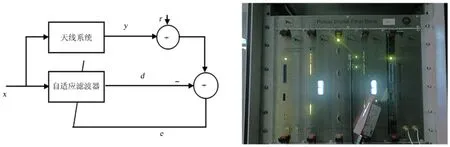
图1 自适应滤波器的工作原理图及南山站的数字滤波器Fig.1 A schematic diagram of an adaptive filter and a picture of the digital filter in the Nanshan station

2 自适应滤波器的原理

根据自适应算法的优化准则的不同，自适应滤波算法可以分为两类最基本的算法:最小均方(LMS)算法和递推最小二乘(RLS)算法。最小均方算法简单，计算量小，容易硬件实现，是目前实际应用中较为广泛也较成熟的一种算法，本文对脉冲星信号进行处理选用的是最小均方算法。

最小均方算法是1960年由Hoff和Widrow提出的最小均方误差算法[5－6]，此算法是基于估计梯度的最速下降算法，算法的判据是基于最小均方误差，即理想信号d(n)与滤波器输出y(n)之差e(n)的平方值的期望值最小，并且根据这个判据修改权系数wi(n)，因此这种算法称为最小均方算法。绝大多数对自适应滤波器的研究是基于由Widrow提出的最小均方算法。这是因为最小均方算法的设计和实现都比较简单，在很多应用场合比较实用。令N阶FIR滤波器的抽头系数为wi(n)，滤波器的输入和输出分别为x(n)和y(n)，则FIR横向滤波器方程可表示为:

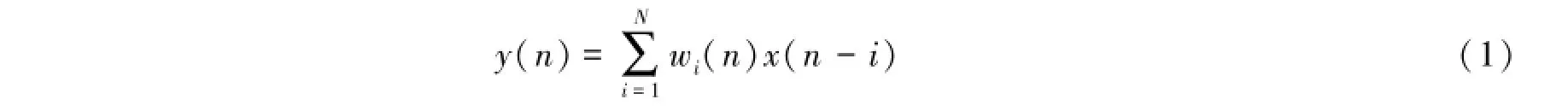
令d(n)代表“所期望的响应”，并定义误差信号:

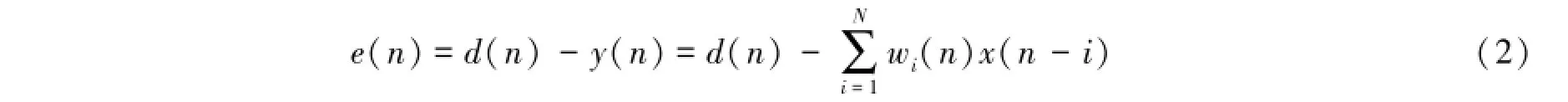
采用向量形式表示权系数以及输入w和X(n)，可以将误差信号e(n)写作:

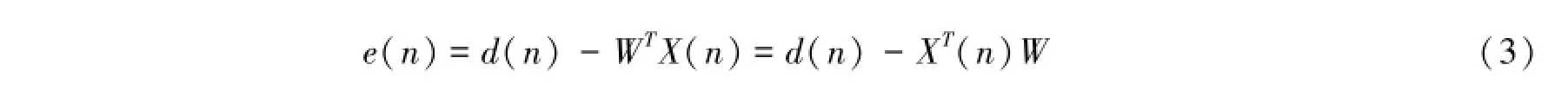
误差的平方为:

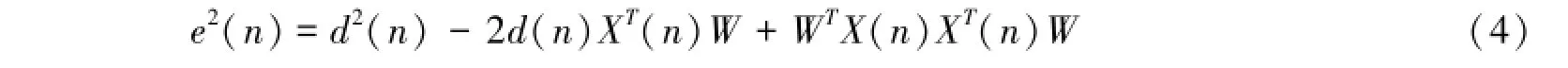
上式两边取数学期望后，得均方误差:

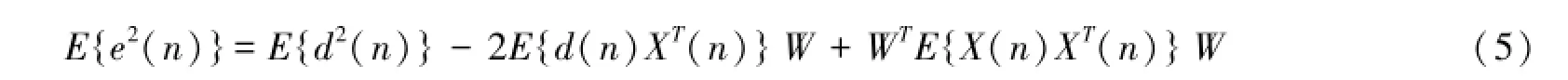
Widrow和Hoff提出了一种在这些先验统计知识未知时求Wopt的近似值的方法，习惯上称之为Widrow-Hoff LMS算法。这种方法的根据是最优化方法中的最速下降法。根据最速下降法，“下一时刻”权系数向量W(n＋1)应该等于“现在时刻”权系数向量W(n)加上一个负均方误差梯度－(n)的比例项，即:

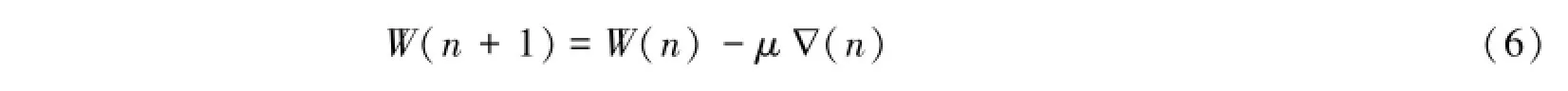
式中μ是一个控制收敛速度与稳定性的常数，称之为收敛因子。因此Widrow-Hoff最小均方算法最终为:

最后，若输出信号y(k)、输出误差e(k)和权系数为W(k)，则最小均方算法递推公式如下:

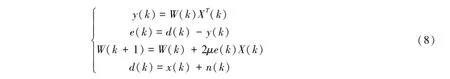
式中，K为迭代次数；M为滤波器的阶数；d(k)表示第k时刻的输入信号矢量；X(k)表示参考信号的信号矢量:

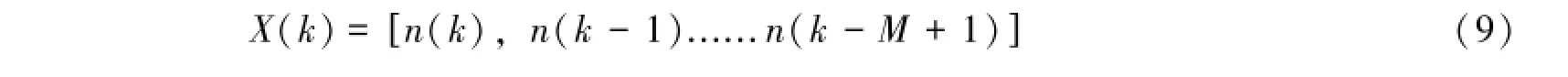
y(k)、e(k)分别表示第k时刻的输出信号与输出误差；W(k)表示k时刻的权系数矢量:

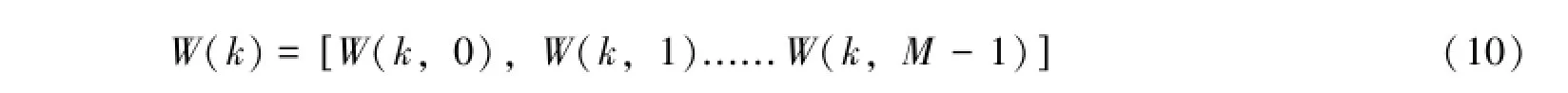
式中μ表示最小均方算法步长收敛因子。自适应滤波器收敛的条件是:

其中λmax是输入信号的自相关矩阵R的最大特征值；μ的选取必须在收敛速度和失调之间取得较好的折中，既要具有较快的收敛速度，又要使稳态误差最小。

3 自适应滤波器的Matlab实现

本文研究了在最小均方算法的基础上，用Matlab软件编写滤波程序实现最小均方误差算法，利用最小均方算法处理脉冲星信号的实现流程如图2。其中基于Matlab的最小均方滤波程序M文件代码如下(脉冲星1910＋0728，第2个脉冲星原理相同):

不同步长因子u的迭代结果不同，步长太长收敛速度较快，误差也较大，步长较小则收敛速度慢，但误差小，这一点在下文的Simulink中得到了验证。本文对新疆天文台南山观测基地观测的脉冲星信号进行了干扰消除算法实验。脉冲星信号依然选用1910＋0728和1913－0440两个信号源，滤波器阶数设置为8阶迭代步长设置为0.000 1，实验发现，对于不同的脉冲星信号源，最小均方算法滤除干扰的效果最好，被选取的脉冲星参考信号基本上可以显示轮廓，两个脉冲星信号的滤波结果如图3。由于南山站是单天线观测，因此对于实验中需要使用的信号无法获取实时的相关信号，为了解决这个矛盾，实验中将天线位置偏离观测源方向2°，采取背景噪声作为本实验的参考信号(图3第2栏曲线)，这个参考信号不具备实时性，相关性也较差，但可以将其信号作为参考样本进行研究，本文将采样信号归一化为512点，在进行滤波之前先进行数据的预处理。

从干扰消除结果上看，在算法上基于Matlab的最小均方自适应滤波器可以很好地消除干扰，凸显脉冲星的轮廓，实现了干扰的消除。

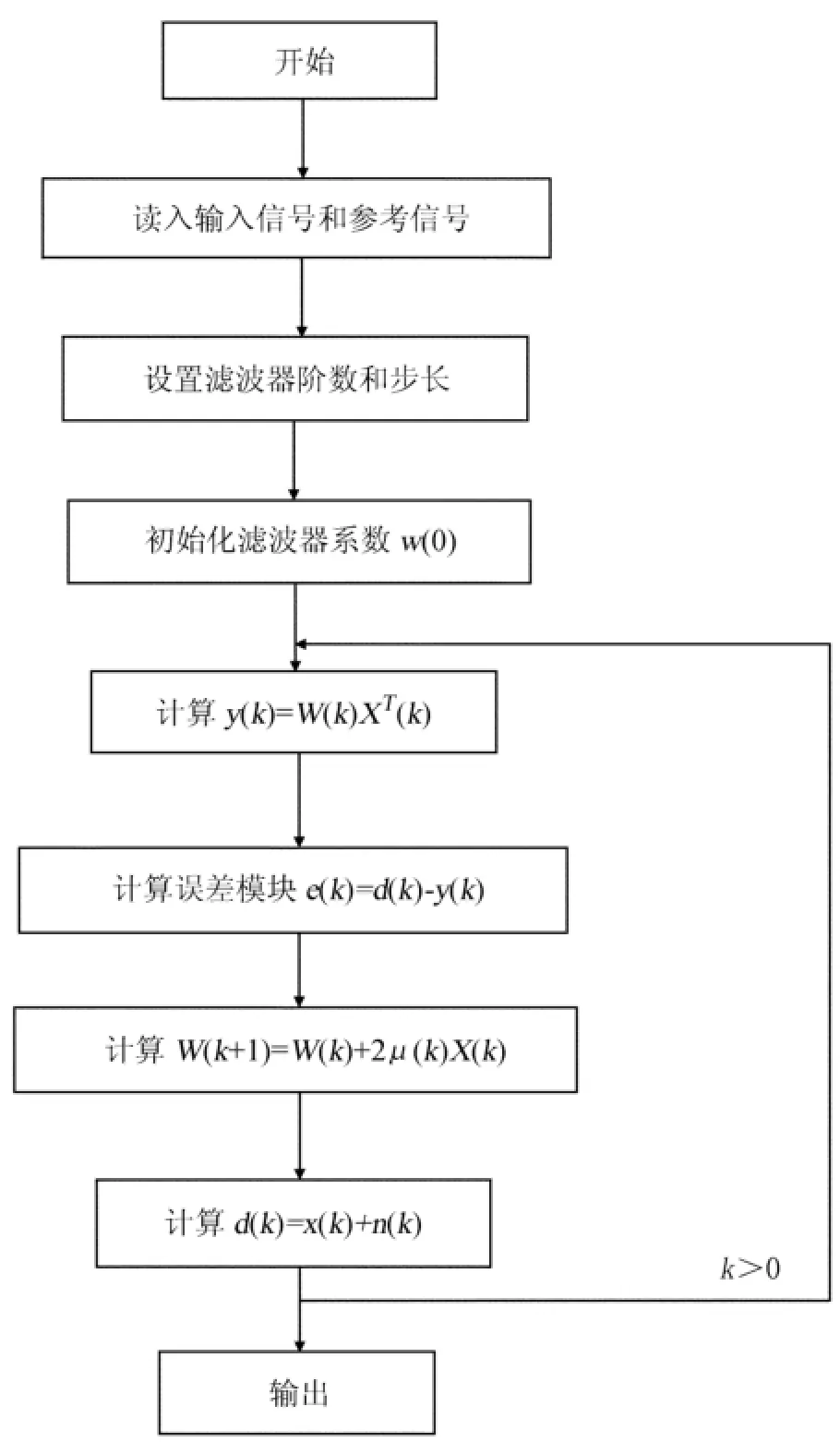
图2 LMS滤波器算法流程图Fig.2 The flowchart of an LMS filter

4 自适应滤波器的Simulink实现

为了获取最小均方滤波器的最优参数，本文在设计最小均方滤波器的时候，首先在Simulink仿真工具箱里对最小均方滤波器建立了一个模型，通过理想信号的输入，对最小均方滤波器的不同参数和性能进行了测试。最小均方的模型如图5。输入信号采用正弦波加入白噪声，参考信号采用白噪声信号。

滤波器的算法采用最小均方误差算法，滤波器的阶数设置为8、32、128等，步长设置为0.01、0.005、0.000 1。滤波器的示波器模块显示的前两栏曲线图中，第1栏表示输入的白噪声信号，第2栏表示输入的参考信号，不论滤波器参数如何变化，这两幅曲线图是相同的，如图5。测试结果如图6、图7、图8(每幅图上、中、下3个子图中第1栏为误差演化；第2栏为滤波输出；第3栏为误差系数)。

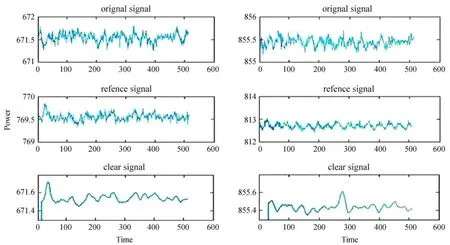
图3 脉冲星1910＋0728(左图)和脉冲星1913－0440(右图)的滤波结果Fig.3 Filtering results of signals from the pulsar 1910＋0728(left-hand panel)and the pulsar 1913－0440(right-hand panel)

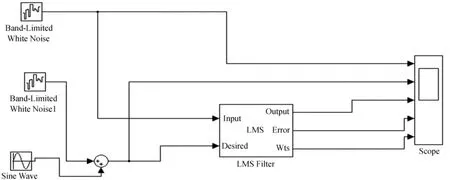
图4 最小均方滤波器的Simulink建模Fig.4 Our Simulink modeling of an LMS filter

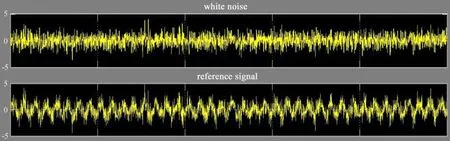
图5 输入信号Fig.5 Input signals

图6 迭代步长0.005，阶数分别为8(上图)、32(中图)、128(下图)的滤波器Fig.6 Test outputs from LMS filters of an iteration step size 0.005.The top，middle，and bottom sets of panels show the outputs from the filters of the orders 8，32，and 128，respectively

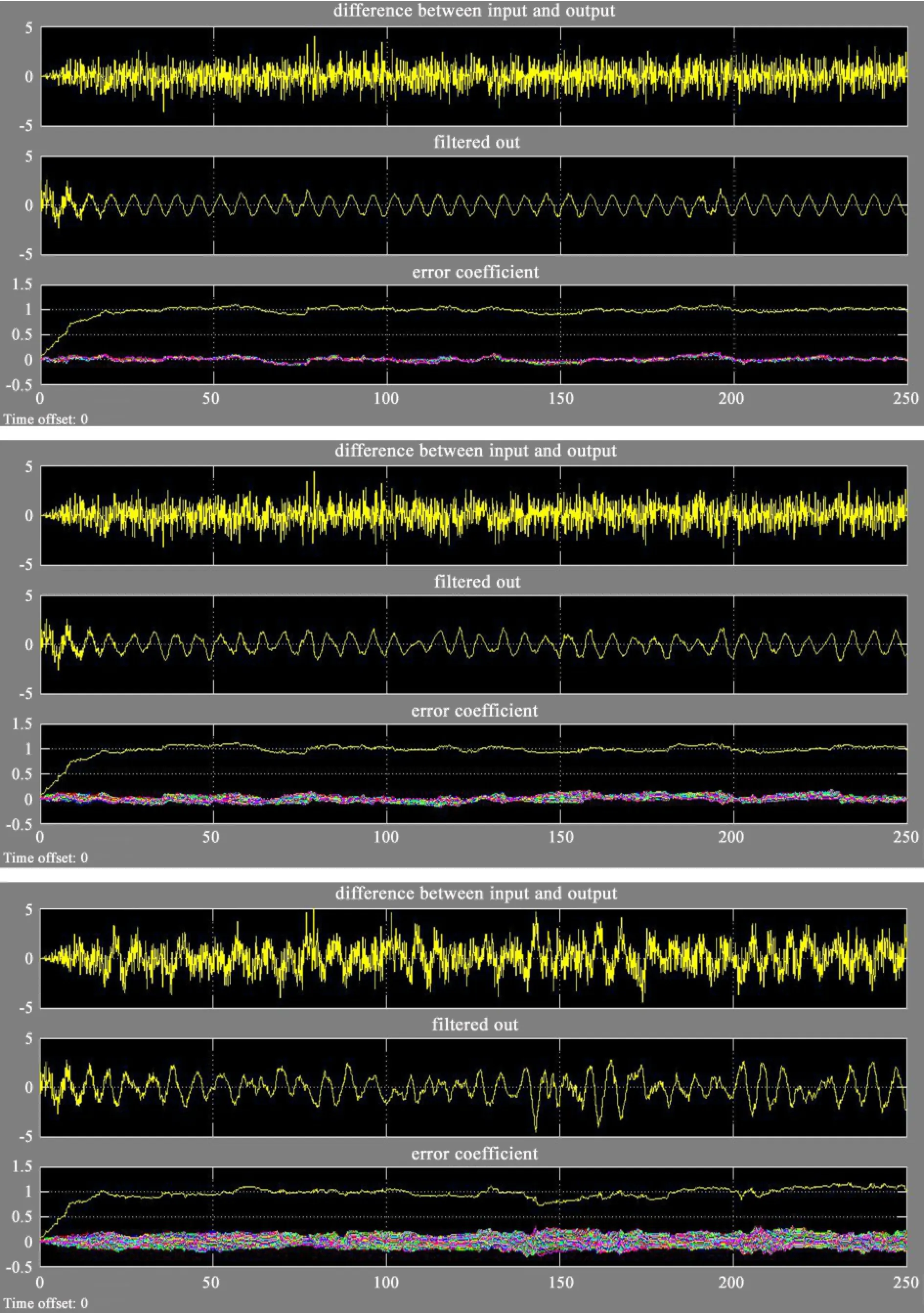
图7 迭代步长0.01，阶数分别为88(上图)、328(中图)、1288(下图)的滤波器Fig.7 Test outputs from LMS filters of an iteration step size 0.01.The top，middle，and bottom sets of panels show the outputs from the filters of the orders 8，32，and 128，respectively

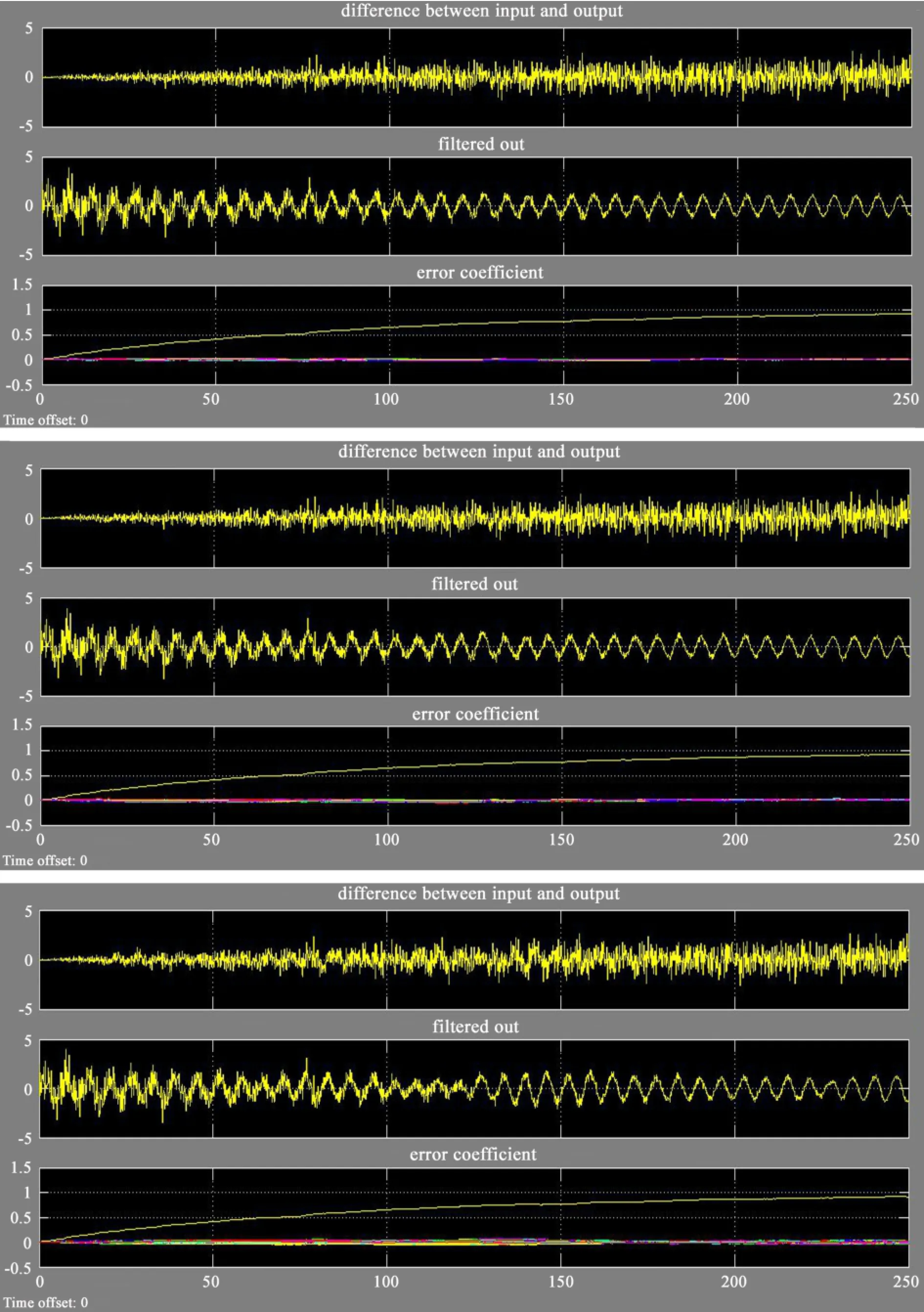
图8 迭代步长0.001，阶数分别为8(上图)、32(中图)、128(下图)的滤波器Fig.8 Test outputs from LMS filters of an iteration step size 0.001.The top，middle，and bottom sets of panels show the outputs from the filters of the orders 8，32，and 128，respectively

5 Simulink仿真结果分析

由以上9幅图像，可以通过对比得出的明显结论是:当步长比较小时，如0.001，滤波器的误差系数在时间上变化缓慢，导致了正弦波噪声在较长的一段时间内无法被有效滤除，如图8上图、中图、下图的滤波输出曲线(第2栏)，因此不能将滤波器的步长设置得太小。另外，为了能够更清晰地做出比较，首先分析当步长一定时改变阶数对滤波效果的影响，比如当步长是0.005时，分别将图6上图、中图、下图的滤波输出曲线的某段时间放大进行对比，如图9，图中从左到右3条曲线依次代表的滤波器的阶数为8、32、128。

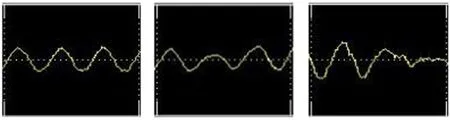
图9 步长不变时阶数升高对滤波效果的影响Fig.9 Outputs from filters of a common iteration step size showing the influences of increasing the filter order

从图中能明显地看出，8阶滤波器滤波效果最好，原有的正弦波得到了较好的还原，而32阶滤波器出现了一定程度的扭曲变形，128阶滤波器变形更严重，甚至出现了数秒钟正弦波幅值为零的情况，这种滤波结果是失败的。由此可以得出结论:当阶数增加时滤波器的性能将变坏，经过反复改变参数，本文最终确定最优的阶数即图6上图所示的8阶。

当滤波器阶数确定时，不同的步长也会明显地影响滤波器性能，明显的结论如图10，阶数同为128，步长分别为0.005和0.01，从图中能看出当步长变大时滤波器的误差系数将变得不稳定，而且噪声很大。因此在保证滤波速度的前提下，应该选择步长较小的滤波器。

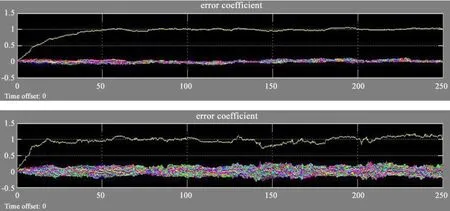
图10 阶数同为128时步长分别为0.005(上图)和0.01(下图)的滤波器的误差系数曲线Fig.10 The error-coefficient curve of a filter of an iteration step size 0.005(the top panel)and that of a filter of an iteration step size 0.01(the bottom panel).The orders of the filters are both 128

经过对系数的反复修改，最终确定了最优的阶数与步长，即图6上图所示的阶数为8阶，步长为0.005的滤波器。

6 结 论

本文利用Matlab和Simulink强大的数值计算和仿真功能，通过不断实验，设计了性能优良的自适应滤波器，得到了能够有效滤除天文台无线电干扰和脉冲星信号噪声的方法。基于新疆天文台良好的实验条件，尤其是借助即将建设的全世界最大口径的新疆110 m射电望远镜这个平台，本文设计的自适应滤波器的实用性和应用前景都非常好，可以满足天文学家对天文观测的技术要求。

[1] Fridman P A，Baan W A.RFI mitigation methods in radio astronomy[J].Astronomy＆Astrophysics，2001，378:327－344.

[2] Jia L Q，Sun Z W，Chen Y，et al.RFI mitigation and implements in radio astronomy[C]// 2011 International Conference on Multimedia and Signal Processing.2011，1:82－85.

[3] 程玉柱，华晋，李赵春.自适应滤波器的算法比较研究[J].大庆师范学院学报，2008，28 (2):23－26.

Cheng Yuzhu，Hua Jin，Li Zhaochun.Comparison study of adaptive filtering algorithm[J]. Journal of Daqing Normal University，2008，28(2):23－26.

[4] 许光辉，胡光锐，宋阳.基于奇异值分解的非线性滤波算法[J].上海交通大学学报，2005，39(4):626－628.

Xu Guanghui，Hu Guangrui，Song Yang.Singular Value Decomposition(SVD)-based nonlinear filtering algorithm[J].Journal of Shanghai Jiaotong University，2005，39(4):626－628.

[5] 陈志军，颜毅华，刘玉英，等.关于中国厘米－分米波频谱日像仪(CSRH)选址与无线电环境监测[J].天文研究与技术——国家天文台台刊，2006，3(2):168－175.

Chen Zhijun，Yan Yihua，Liu Yuying，et al.Site survey and RFI test for CSRH[J]. Astronomical Research＆Technology——Publications of National Astronomical Observatories of China，2006，3(2):168－175.

[6] 贺宽，黄涛.基于Matlab的自适应滤波器设计[J].武汉理工大学学报:信息与管理工程版，2008，30(1):70－73.

He Kuan，Huang Tao.Adaptive filter design based on Matlab[J].Journal of Wuhan University of Technology:Information＆Management Engineering，2008，30(1):70－73.

Simulations of Adaptive Filters of Antenna Systems Based on the Matlab/Simulink Tools

Hu Kaiyu1，2，Aili Yusup1，Liu Qi1
(1.Xinjiang Astronomical Observatory，Chinese Academy of Sciences，Urumqi 830011，China，Email:hukaiyu＠xao.ac.cn；2.University of Chinese Academy of Sciences，Beijing 100049，China)

In order to make signals received by radio-telescope antenna systems more clearly recognizable，i.e.with system noise and electromagnetic interferences reduced to desired levels，we design a type of adaptive filters and numerically simulate their performances using the powerful Matlab/Simulink tools.Ouradaptive filters are to meet the special requirements on radio-astronomy observations and deep-space explorations(of the Moon and Mars)at the Nanshan Station of the Xinjiang Astronomical Observatory，Chinese Academy of Sciences.In an earlier section of this paper we present signals from the pulsars 1910＋0728 and 1913－0440(Liu Qi，private communication)，which serve as reference signals for testing the filters.We write an algorithm in a Matlab M-file realizing the adaptive filtering.The file is easily understandable and allows other people to study.Our simulation tests with the pulsar signals show that the filters can effectively reduce the noise.In addition，we use the Simulink in the Matlab for modeling and simulating antenna systems(including the filtering).By extensively changing the order and the iteration step size of a modeled filter，we find the optimal parameters for our adaptive filter:an order of eight and a step size of 0.005.In the process，we have also verified that filters of this type can effectively restore profiles of received signals and minimize errors while fast processing signals.The simulation results and subsequent analyses of these(particularly the results with the Simulink)show that our adaptive filters can practically result in fine outputs and meet the needs of radio astronomy.With the rapid development of radio astronomy in China and the progress of building the 110m radio telescope in Xinjiang，filters as ours will be widely used for deep-space explorations and astronomical observations.

Antenna；Adaptive filter；Pulsar；Simulation

TN911.4

A

1672－7673(2014)03－0264－11

2013－10－23；

2013－11－08

胡开宇，男，硕士.研究方向:天文技术与方法.Email:hukaiyu＠xao.ac.cn