隔振数控机床的轮廓误差控制方法研究

杨 洋，李金良，李晓春，周 亮

（1.吉林大学 工程训练中心，长春 130025；2.吉林大学 材料科学与工程学院，长春 130025）

隔振数控机床的轮廓误差控制方法研究

杨 洋1，李金良2，李晓春1，周 亮1

（1.吉林大学 工程训练中心，长春 130025；2.吉林大学 材料科学与工程学院，长春 130025）

0 引言

机床在加工过程中会受到加工载荷导致的颤振与惰性力传递的振动，这两种振动都会导致加工表面质量下降，甚至会损坏机床或者零件[1～4]。加工载荷引发的振动可以通过在数控程序中选择合适的切削深度和主轴转速来避免，惰性力振动常发生在大质量机床组件加速的过程中[5,6]。本文给出一种结合修正输入和轮廓误差补偿的方法来减少惰性力引发的振动。在工业中的惰性振动通常由在位置反馈上采用滤波器的方法来进行避免，因此振动频率不会传递到控制器中，但是这种方法却会减小驱动的带宽，所以这不是提高机床精度的理想方法[7]。可以在不同的控制律中采用位置或加速度反馈的方法来减小振动，然而这种方式不但给驱动信号带来了高频成分，还需要增加一些额外的传感器来测量振动信号，并且难以整合到数控系统中去。Singer[8]提出了输入修正方法来避免触发机构的振动频率，Dietmair[9]在数控机床线性驱动上应用命令修正方法，结果显示在高速定位过程中，瞬态振动达到了最小。尽管输入修正在单轴定位上取得了一定的效果，但是应用到多周的时候会增加轮廓误差[10,11]。当修正多轴轨迹生成命令来避免振动时，依靠运动轴的路径会发生变形，从而增加了轮廓误差。由于带宽和动态导致的轴控制器滞后位置命令造成的轮廓误差，在轮廓加工中主要依赖于各个驱动的路径形态及跟踪误差。Koren[12]提出一种简单的交叉耦合控制器来估计和最小化两轴轮廓误差。Chen[13]提出一种跟踪误差与轮廓误差的几何关系，并通过交叉耦合命令修正控制器来提高轮廓精度。Altintas[14]提出一种滑模控制器来预测和补偿五轴刀具路径的轮廓误差。机床的结构振动在以前的轮廓误差控制器中并未考虑。因此本文提出结合隔振和轮廓误差补偿的方法来用于多轴数控机床。

1 隔振下的轨迹修正

定义进给驱动i的结构动力学模型为有阻尼的二阶系统，表示如下：

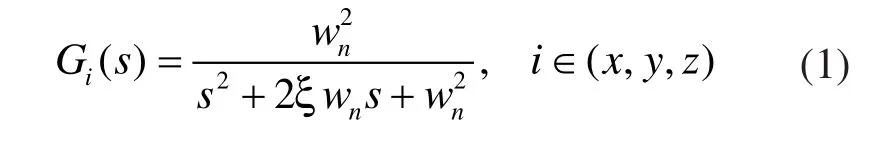
其中，nw与ξ为固有频率和阻尼率。轨迹修正的目标是将由结构模型造成的残余振动减少至0，用到哦脉冲信号的卷积方法，也称为输入修正，将离散位置命令施加到每一根轴的伺服系统，带阻尼驱动对于jt时刻幅值为jA的脉冲信号的响应为：

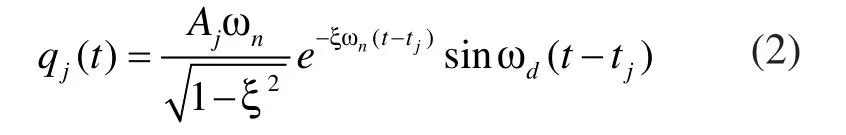
可以通过减小振幅至零来缩小残余振动，也导致了零振动整形：

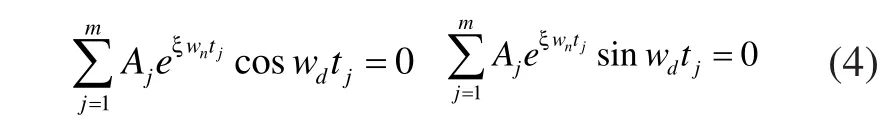
隔振的鲁棒性阻止了结构动力学沿着刀具路径变化，通过设置残余振动的振幅微分来进行提高，同时考虑了固有频率趋于零[3]：

零振动和微分输入修正器，有三个施加在tj=0,0.5Td,Td的脉冲组成，经常在实际应用中得到零残余振动，鲁棒性阻止了固有频率在15%-20%内的变化。零振动和微分输入修正器的方程可以表示为：

通过建立安全生产管理体系，加强危险源辨识、评价的培训，切实落实危险源控制工作，以提升危险源控制与管理水平。利用安全工作例会机会检查危险源辨识工作开展情况，逐一点评，统一思路，相互借鉴，促进危险源辨识工作水平提升。

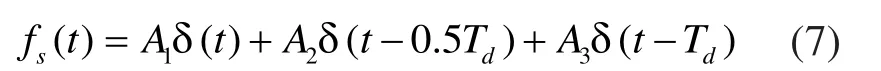
在数控系统的实时间隔中采用以下递归算法：

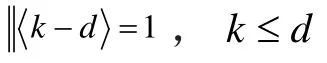
2 轮廓误差补偿

引入驱动伺服带宽导致的跟踪误差，输入修正由于延迟项(t− (j− 1 )Td/2)会带来额外的误差，这个增加的跟踪误差会导致沿着曲线刀具路径的大的轮廓误差。如果不进行补偿，则输入修正将不能够抑制机床的残余振动。

本文给出一种在控制环之前的进一步修正位置命令的预补偿方法，为了能够实现轮廓误差补偿技术，首先将轮廓误差用一种已有的方法估计出来，如图1所示一个三轴刀具路径样例，其中Pd和Pa代表着理想刀尖位置和实际刀尖位置，跟踪误差e定义为实际位置和理想位置之间的差值：

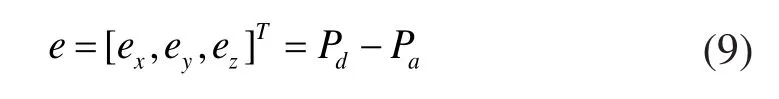
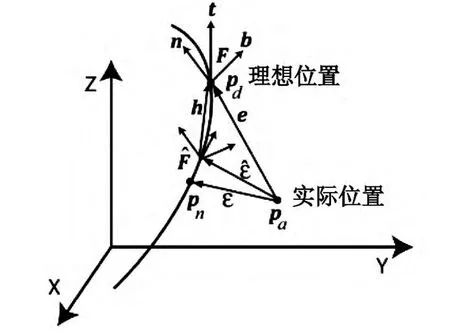
图1 三轴刀具路径轮廓误差估计

轮廓误差ε为实际刀具路径与理想刀具路径的偏差情况，定义为刀具路径跟踪误差的法向分量：

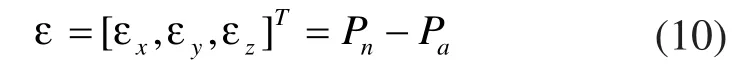
其中，Pn用解析的方法很难去估计。由Erkorkmaz等人提出的迭代轮廓误差估计具有一定的预测精度，但是在计算极其复杂。本文使用的是由Altintas等人提出的用弗雷涅漂移方法直接估计轮廓误差。

弗雷涅漂移方法中，随着参考位置移动，由多正交单元正切 n(t)，向量 n(t)，双向量 b(t)来定义，如图1中：

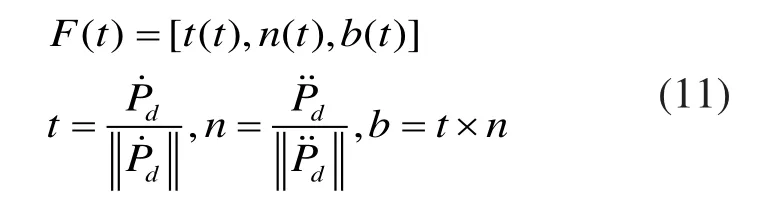
然而，由机床动态或者输入修正导致的跟踪误差，具有一个延迟时间dt的实际响应滞后可以估计为：

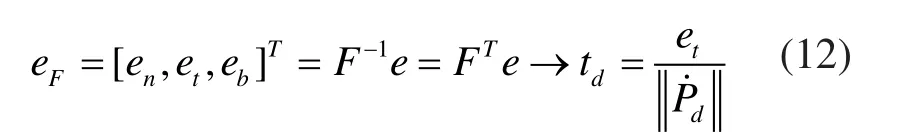
其中，eF为跟踪误差向量，延迟位置向量h和弗雷涅漂移定义为：

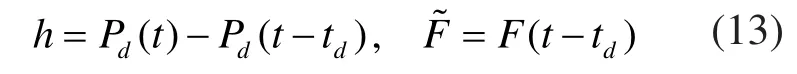
最终的轮廓误差向量可以估计为：

其中，n～和b～在工件坐标系中代表的是弗雷涅漂移的法线方向和双法线方向。本文提出的结合输入修正的前馈命令修正轮廓误差补偿技术如图2所示。

图2 带轮廓误差补偿的命令修正模块流程图

为了简化说明，图2中只给出了X轴和Y轴，但是所提出的方法可以用于五轴命令修正。由插补器和轨迹生成算法产生的参考轴的起始位置命令通过式（9）输入修正器第一次滤波。输入修正器消除了激励机构固有频率引起的谐波效应，但是却带来了刀具路径失真和大的轮廓误差，轮廓误差预补偿方式如下：

进给驱动刚体i的闭环传递函数假设有如下离散形式：

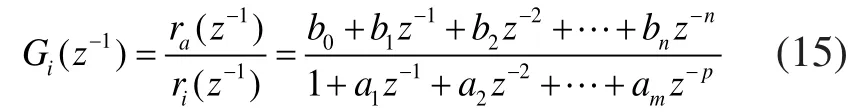
驱动的实际位置可以假设为：

采用机床的正运动学将式（16）预测的运动轴位置映射到工件坐标系中，预测的刀尖位置与起始位置之间的轮廓误差，未修正刀尖位置命令由式（14）来估计。采用机床的逆运动学将计算的轮廓误差向量反映射到各个轴来确定相应的补偿项。然而，预测的轮廓误差信号通常具有高频振荡，主要由驱动的动力学特性和外界的干扰激发，因为补偿方法目的是减小轮廓误差的中频误差和低频误差项，所计算的补偿信号采用低通滤波器来进行滤波，最终，过滤的补偿信号增加到输入修正参考命令来预补偿轮廓误差：

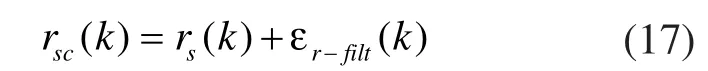
式（17）改进的位置命令，施加到实际轴的控制环，可以减小驱动机构的残余振动和轮廓误差。

3 实验结果

本文所提出的隔振情况下的轮廓误差控制方法在一个两轴机构上进行试验，两轴线性电机驱动平台如图3所示。

图3 线性电机驱动XY平台

将驱动的控制参数调节到未匹配有阻尼动力学下来验证本文方法的有效性，两轴用于输入修正滤波器建模的固有频率和阻尼率为：

X轴和Y轴修正器设计为卷积的形式，这样形成的XY修正器可以同时修正两个轴：

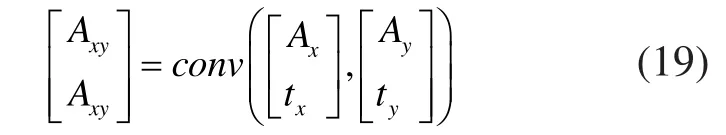
驱动的闭环传递函数为：

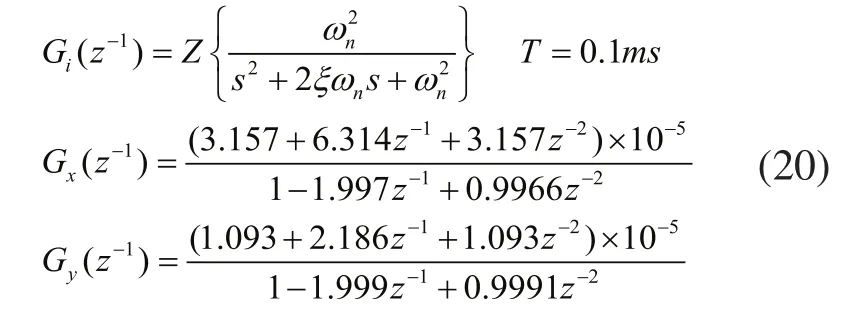
在XY两轴运动信号存在一定的相位差时，可以合成一个圆轨迹，如图4所示。

图4 圆刀具路径和相应的轴位置命令

形成的圆轨迹的半径为40mm，此时的进给率f=80mm/s。需要注意的是刀具路径轨迹的起始点不是从正90°开始，这样两个轴都可以被激励。

试验测量了X轴和Y轴的跟踪误差，如图5所示。

图5 未修正和修正后的跟踪误差

当位置命令直接施加到有阻尼的驱动时，每个轴在其固有频率附近产生了大振幅的振动，当位置命令由滤波器（式（8））进行修正后，跟踪误差从振幅上面显著的减小。然而，输入修正滤波器由于时间延迟增加了轮廓误差，如图6所示。

图6 未修正，修正以及修正并补偿的轮廓误差与补偿信号

通过本文提出的方法，对于输入修正滤波器进行误差补偿，同样的刀具路径轨迹如图6所示，由于采用低通滤波器来减小震荡，通过误差补偿后的轮廓误差和震荡情况显著的减小。

4 结论

机床在高速和高加速度操作中容易产生残余振动和轮廓误差，振动主要由于机床的机构模型产生，轮廓误差源由伺服驱动带宽限制或者用于产生轨迹命令的隔振方法导致，本文提出一种隔振情况下结合轨迹命令修正的误差补偿控制方法，由驱动的闭环传递函数和机床运动学来估计轮廓误差，并在控制环进行前馈补偿，并在一个XY运动平台上进行试验，试验的结果表明，采用本文提出的方法，可以有效的减小轮廓误差和震荡情况。

[1]Altintas Y,Verl A, Brecher C, Uriarte L,Pritschow G.Machine Tool Feed Drives.CIRP Annals ,2011,60(2):779-796.

[2]Erkorkmaz K,Yeung CH, Altintas Y.Virtual CNC System.Part II. High Speed Contouring Application. International Journal of Machine Tools and Manufacture ,2006,46(10):1124-1138.

[3]彭振洲.直线电机驱动的数控机床XY工作台轮廓误差控制系统设计[D].电子科技大学,2013.

[4]李学伟,赵万华,卢秉恒.轨迹误差建模的多轴联动机床轮廓误差补偿技术[J].西安交通大学学报,2011, 3(46):48-52.

[5]王广炎,张润孝,帅梅,王小椿.数控机床的轮廓误差的控制[J].机床与液压,1999,6:59-61.

[6]SinghoseWE,Seering WP,Singer NC.Improving Repeatability of Coordinate Measuring Machines with Shaped Command Signals. Precision Engineering,1996,18(2–3):138-146.

[7]于洋,张为民,来燕菁.PLC在数控机床轮廓误差控制中的应用[J].制造业自动化,2011,7(33):32-34.

[8]Singer NC, Seering WP .Preshaping Command Inputs to Reduce System Vibration. ASME Journal of Dynamic Systems Measurement and Control ,1990,11(2):76-82.

[9]Dietmair A,Verl.A Drive Based Vibration Reduction for Production Machines.Modern Machinery Science Journal ,2009,3(4):112-119.

[10]肖本贤.多轴运动下的轮廓跟踪误差控制与补偿方法研究[D].合肥工业大学,2004.8.

[11]肖本贤,王群京,昂卫兵,娄天玲.基于神经网络的轮廓误差控制仿真研究[J].系统仿真学报,2003,4(15):572-574.

[12]Koren Y,Lo CC .Variable-gain Cross-coupling Controller for Contouring.Annals of CIRP,1991,40(1):371-374.

[13]Chen CS, Chen LY.Cross-coupling Position Command Shaping Control in a Multi-axis Motion System.Mechatronics,2011,21(3):625-632.

[14]Altintas Y, Sencer B.High Speed Contouring Control Strategy for Five-axis Machine Tools. Annals of CIRP ,2010,59(1):417-420.

Contour error control method of CNC machine tools under vibrate isolation

YANG Yang1，LI Jin-liang2，LI Xiao-chun1，ZHOU Liang1

针对机床在加工过程中的颤振与惰性力传递振动，提出了一种进给驱动的隔振以及轮廓误差

补偿算法。首先在参考轴的命令信号中施加输入修正滤波器来避免残余振动，所施加的输入修正滤波器可以结构模态激振，但是会增大跟踪误差和轮廓误差。所提出方法的跟踪误差由驱动轴的闭环传递函数来估计，同时用来预测映射到每一根轴的轮廓误差，预测的结果用来进行预补偿。将所提出方法通过在XY两轴平台上进行试验，验证了结合隔振和轮廓误差补偿方法的有效性，试验结果表明所提出方法能够提高了阻尼和轮廓精度。

隔振；数控机床；轮廓误差；误差控制；误差补偿

杨洋（1984 -），女，吉林通化人，助理工程师，硕士研究生，研究方向为高校工程训练教学管理。

TH161

A

1009-0134(2014)06(上)-0053-04

10.3969/j.issn.1009-0134.2014.06(上).15

2014-03-20