基于Raleigh-Ritz的五自由度并联机床刚度分析及仿真
2014-05-11贾艳丽
贾艳丽,刘 岩
(南阳理工学院 软件学院,南阳 473000)
基于Raleigh-Ritz的五自由度并联机床刚度分析及仿真
贾艳丽,刘 岩
(南阳理工学院 软件学院,南阳 473000)
0 引言
并联机床(Parallel Machine Tool, PMT)是一种新型机床,具有精度高、响应快和刚度大等特点[1~3]。并联机床的高刚度特性可以在高速金属加工过程中,保证加工精度以及提高刀具使用时间[4,5],因此刚度是并联机床设计制造过程中的重要指标,对并联机床的性能有着重要指导意义[6]。并联机床的刚度分析通常采用结构矩阵分析法、雅克比矩阵法以及假设模态法等数值方法以及Anasys软件模拟方法等,其中数值方法虽然能够在工作空间内进行分析,但是建模过程复杂,通用性不强,而软件模拟方法适合针对某一固定位置进行刚度分析,不适合对并联机构的工作空间刚度进行分析[7,8]。为解决以上问题,本文根据有限元基本原理,对一种五自由度并联机床进行了刚度分析,并进行了刚度仿真,为并联机床的优化设计及性能分析提供了一定的理论基础。
1 并联机床机构分析
五自由度并联机床是一种五自由度虚拟轴机床,主要有动平台、静平台、驱动支链以及约束支链构成,机构拓扑图如图1所示,静平台上设有全局坐标系OA-XAYAZA,动平台上设有动坐标系OB-XBYBZB,假设Ri表示Ai与OA之间的距离,iθ表示OAAi与XA轴之间的夹角,ri表示Bi与OB之间的距离,iϕ表示OBBi与XB轴之间的夹角,其中i=1,2,…,5。
通过机构分析可以知道,中间支链具有5个刚体自由度,由此可知中间支链不会影响动平台其他5个自由度方向的刚度,因此进行刚度分析时可以忽略中间支链,根据有限理论对并联机床进行机构离散,离散化模型如图2所示。
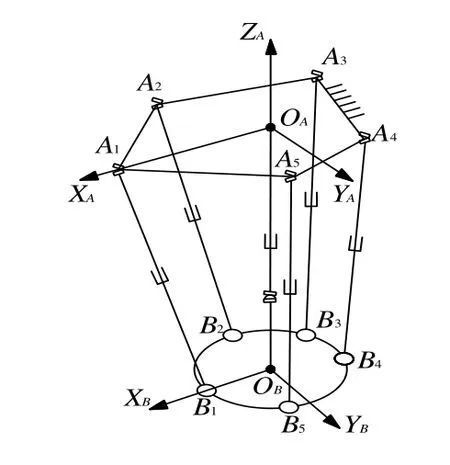
图1 并联机床拓扑图
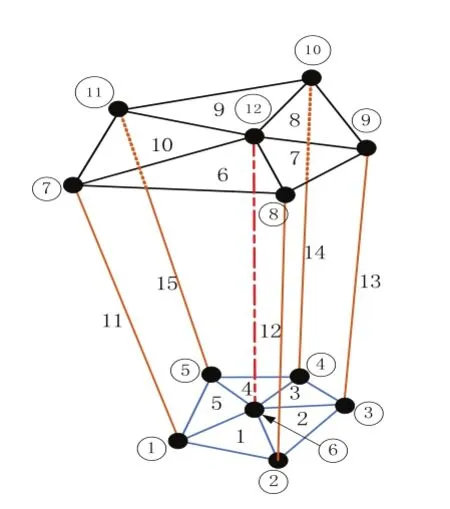
图2 并联机床离散化
2 有限元单元刚度分析
根据五自由度并联机床机构特性及离散化后的有限元模型可知,构成五自由度并联机床的基本有限元单元有两类,一类是空间三角单元,此类单元有1~10。第二类基本单元是空间杆单元,此类单元是11~15,因此需要对以上两种单元进行有限元刚度建模。本文采用的建模方法是Raleigh-Ritz方法。首先建立空间杆单元有限元刚度模型,在外力的作用下单元上的平衡方程为一维微分方程。设坐标x处的应力分布为σ(x),截面积为A(x),轴向外力为f(x),则杆单元在该处的应力为σ(x)A(x),可以得到如下的基本方程:
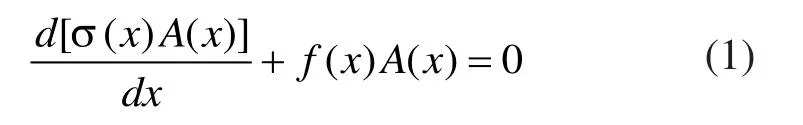
由Hooke定律可以得到位移u(x)的二阶微分方程:

根据最小势能原理,公式(2)的变分函数如下所示:

其中abr是积分常数。
设单元节点位移构成的位移响亮为{u},形函数矩阵为[N],可以得到:

将公式(5)带入公式(4)中,并带入单元的材料等参数,可以得到带有形函数形式的变分函数,并进行变分求解进行极小化,如公式(5)所示:

通过矩阵计算,可以得到局部坐标系下的刚度矩阵KL,通过Z-Y-X形式的欧拉角变换矩阵R,可以得到全局坐标系下的刚度矩阵KG,如公式(6)所示。

通过得到的各个单元在全局坐标系下的刚度矩阵,根据有限元原理,可以得到五自由度并联机床的刚度矩阵K。对刚度矩阵K进行边界条件处理后既可以得到并联机床的刚度分布情况。
3 仿真及模拟分析
3.1 刚度分布仿真分析
机构的刚度特性和机械结构密切相关,五自由度并联机床的结构如表1所示,根据给定的物理参数,支链的截面积简化为7.8×10-4m2,动平台、静平台及支链的弹性模量均设为2.03×1011N/m2。五自由度并联机床有五个自由度,其中沿X、Y两个方向的刚度值对加工质量的影响最大,设α为动平台相对静平台绕Y轴的转角。

表1 并联机床主要结构参数
此并联机构具有5自由度,为了能够在笛卡尔坐标系表示机构的刚度特性,在此固定1个方向的自由度,其余两个自由度在笛卡尔坐标系X-Y平面内表示,用Z表示机构的静刚度特性。分别假设α=0°和α=25°两种条件下,采用极坐标搜索形式数值求解位置工作空间,进行静刚度分析,结果如图3所示。
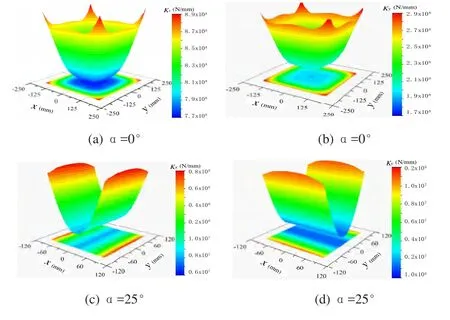
图3 刚度分布
从图3中可以看出,当α=0°时X与Y方向的刚度明显大于α=25°时的对应刚度,说明动平台平行于静平台时刚度特性优良,并且中间刚度位置低于边界值,是由于处于边界位姿时靠近机构的奇异位置引起的。机构刚度的最小值出现在工作空间的中心处,并且最小刚度值都大于允许刚度值,表明并机床的静刚度满足静刚度指标。在同一位置时X、Y两方向的刚度也不相同,符合机构各向异性的机构特性。为检验计算结果,利用有限元软件对并联机床的中心位置进行了刚度模拟仿真。
3.2 刚度模拟仿真分析
为进行软件仿真,首先建立五自由度并联机床的三维模型,通过网格划分以及边界条件设定,进行刚度模拟仿真,图4为弹性变形的结果图。
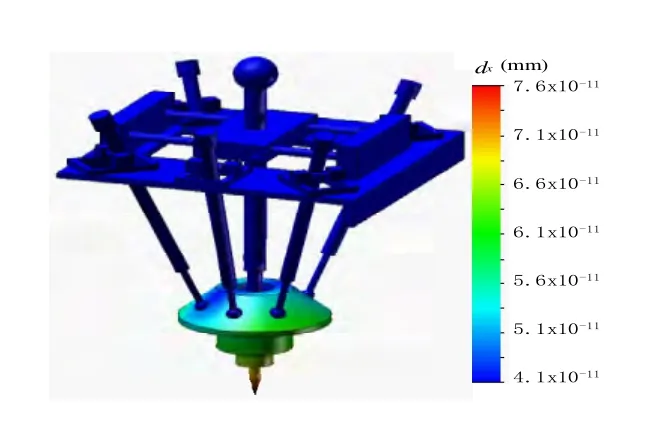
图4 刚度模拟仿真弹性变形结果
根据图4所示的弹性变形,利用胡克定律得到该位姿下动平台中心点处的X方向刚度,计算结果为5.9×108N/m,该位姿情况下有限元理论计算结果为6.2×108N/m,与图4中所示的结果进行对比分析,相对误差为4.76%,造成误差的主要原因在于对球副的简化以及动平台的简化分析,但是结果的误差满足工程应用,表明了Raleigh-Ritz方法对并联机床进行刚度分析的有效性。
4 结论
通过对五自由度并联机床进行机构特性分析,确定了构成并联机床的基本有限单元,然后通过Raleigh-Ritz方法得到单元及整体的刚度矩阵,通过整体刚度矩阵对五自由度并联机床进行了刚度计算,得到了工作空间的刚度分布情况,并利用有限元软件进行了刚度仿真,通过对比两种方法得到的刚度结果,验证了Raleigh-Ritz方法分析静刚度的正确性,并表明了并联机床的静刚度满足工作需求。Raleigh-Ritz方法相对于其他刚度分析方法建模过程清晰,并适合计算机自动求解,对并联机床的可靠性以及并联机床的优化设计具有一定的理论指导意义。
[1]李长河,蔡光起.并联机床发展与国内外研究现状[J].青岛理工大学学报,2008,29(01):7-13.
[2]汪劲松,黄田.并联机床-机床行业面临的机遇与挑战[J].中国机械工程,1999,10(10):1103-1107.
[3]段广洪,李铁民.并联机器的起源和发展[J].世界制造技术与装备市场,2006(1):41-48.
[4]孟祥志.一种新型立卧转换式三杆混联机床的设计研究[D].沈阳:东北大学,2004.
[5]Kim B H,Park T,Shin H Y, et al.A comparative study of the tension estimation methods for cable supported bridges[J].Steel Structures,2007,7(3):77-84.
[6]Krenk S.Complex modes and frequencies in damped structural vibrations[J].Journal of Sound and Vibration,2004,270: 981-996.
[7]吴海兵,刘远伟,左敦稳.交叉式并联机床工作空间分析[J]. 机械科学与技术,2009,28(4):472-475.
[8]徐开元,徐武彬,唐满宾.基于有限元的机床滑鞍结构的动特性分析[J].机械设计与制造.2011(04),170-173.
Stiffness analysis and simulation of 5-dof parallel machine tool based on raleigh-ritz method
JIA Yan-li,LIU Yan
针对软件模拟方法适合某一固定位置的刚度分析,不适合对并联机构的工作空间刚度分析的问题,提出了一种基于Raleigh-Ritz的五自由度并联机床刚度分析方法。首先利用有限元基本原理对并联机床的机构分析离散出基本单元,然后利用Raleigh-Ritz方法计算出基本单元的刚度矩阵,装配后得到系统刚度矩阵,最后通过系统刚度矩阵对并联机床的刚度进行了分析,得到了并联机床工作空间内的刚度分布,并利用刚度分析软件进行了仿真实验,对分析结果进行了对比分析,为并联机床的优化设计提供了理论依据。
Raleigh-Ritz方法;有限元理论;并联机床;刚度矩阵
贾艳丽(1977 -),女,河南新野人,讲师,硕士,研究方向为软件设计与数据挖掘。
TP193
A
1009-0134(2014)06(上)-0098-03
10.3969/j.issn.1009-0134.2014.06(上).29
2014-03-20
河南省科技攻关计划项目(A13060232)
