基于遗传算法和神经网络的矮小儿童智能诊断研究

张京军，王 健，邵伟东，高瑞贞

(1. 河北工程大学 信息与电气工程学院，河北 邯郸 056038；2. 石家庄展望未来科技有限公司，河北 石家庄 050081)

矮小是危害人们身心健康的主要外在表现之一，它不仅仅是患者的个人问题，又是不得不面对的社会问题。而通过先进的信息技术将具有该领域医疗专家水平的计算机辅助诊断系统应用到医疗机构，一方面可以大大提高诊断效率与准确率，另一方面也有利于患者的及时就诊。从20世纪70年代末开始至80年代中期，我国先后出现一批医学诊断专家系统软件[1]，早期的有上海计算所的中医妇科诊断系统、吉林大学和白求恩医科大学合作的妇科专家系统等。近期的有上海中西医结合医院与颐圣计算机公司联合开发具有咨询和辅助诊断性质的计算机辅助诊疗系统等。当前的人工智能技术发展已经较为成熟，尤其是神经网络技术在诸多工程领域的应用日趋广泛，而利用遗传算法来优化神经网络并应用到医学辅助诊断领域的研究尚处于初级阶段。鉴于此，本文利用遗传算法来优化矮小儿童智能诊断的神经网络模型。

1 临床数据预处理

1.1 矮小症病例样本数据规范化

本文采取石家庄展望未来科技长期跟踪监测研究数据(所有检查结果均来自于国内各地正规医院)，对影响儿童身高发育的病因进行分析训练和仿真。根据资料分析以及专家经验确定影响儿童身高发育的主要因素[2]和检查项目,并将之列为神经网络的输入数据：患儿性别，实际年龄，体重，现身高，CHN骨龄，BMI(Body Mass Index身体质量指数)评价，父身高，母身高，生长激素水平(GH)，血清总三碘甲状腺原氨酸(TT3)，血清总甲状腺素(TT4)，促甲状腺激素(TSH)，促黄体生成素(LH)，胰岛素样生长因子1(IGF-1)，胰岛素样生长因子结合蛋白3(IGFBP-3)，微量元素，脑CT。其中患儿性别、微量元素、脑CT都是非数值形式，不能直接被BP网络识别，必须对其进行数值化。分别用1，0代表性别属性中的男和女，微量元素的不缺乏和缺乏，脑CT影像检查结果的正常和异常。

诊断结果为8种常见的矮小病因类型，并将其作为神经网络的期望输出模式：遗传性矮小(0 0 0)，体质性青春期发育迟缓(0 0 1)，原发性GHD(0 1 0)，甲状腺功能障碍(0 1 1)，营养性矮小(1 0 0)，继发性GHD(1 0 1)，性早熟(1 1 0)，其他疾病(1 1 1)。

1.2 实验数据归一化

对于样本数据属性的差异问题运用数据归一化方法对神经网络输入数据进行预处理，使数据分布在[-1，1]的区间上，以便于神经网络的快速收敛从而得出正确的诊断结果[3]。

Pn=2*(P-minp)/(maxp-minp)-1

(1)

Tn=2*(T-mint)/(maxt-mint)-1

(2)

这里，P和T分别为样本中待处理的输入数据和原始的目标数据，Pn和Tn为经过归一化处理后的输入数据和目标数据。矮小儿童病例数据归一化后的结果如下表1所示：

2 矮小儿童智能诊断模型

矮小儿童智能诊断的数学模型是基于BP算法[4]的数学模型。BP网络的学习是信息的正向传递和误差的反向传播，通过不断修正权值来使目标输出与期望输出更加接近。

三层感知器中，输入向量为x=(x1,x2,…,xn)T，其中x0=-1是为隐层神经元引入阈值而设置的；隐层的输入向量为y=(y1,y2,…,ym)T，其中y0=-1是为输出层神经元引入阈值而设置的；输出层输出向量为o=(o1,o2,…,ol)T；期望输出向量为d=(d1,d2,…,dl)T。输入层到隐层之间的权值矩阵用v=(v1,v2,…,vm)T表示；隐层到输出层之间的权值矩阵用w=(w1,w2,…,wi)T表示。

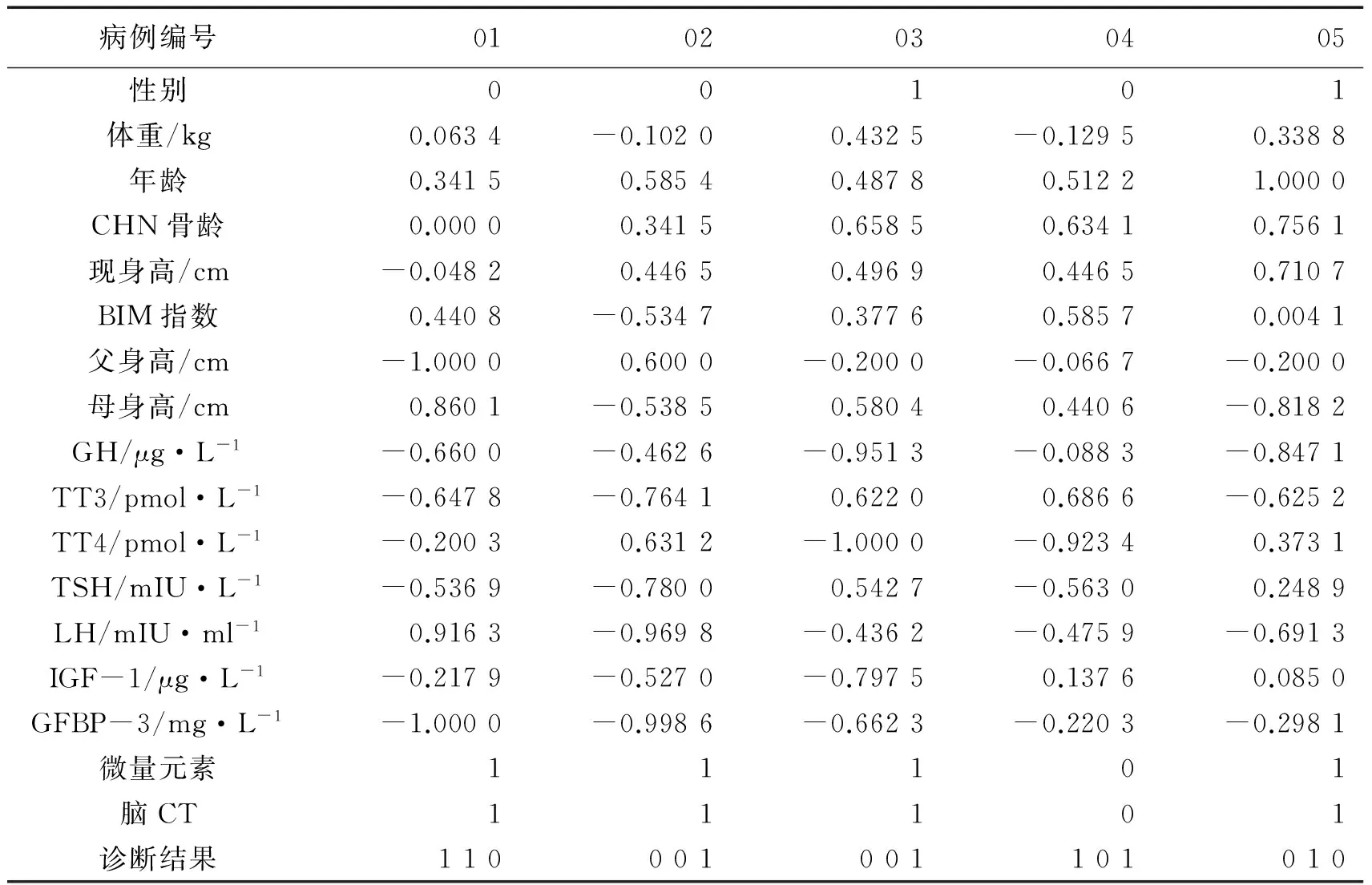
表1 病例样本归一化数据表

对于输出层，有

ok=f(knet)

(3)

对于隐层，有

yj=f(jnet)

(4)

当网络输出与期望不等时，存在输出误差E，定义如下：

(5)

将式(3)扩展至隐层与输入层，有

(6)

(7)

相应得出的三层感知器的BP学习算法权值调整计算公式为

Δwjk=ηδk0yj=η(dk-ok)ok(1-ok)yj

(8)

(9)

3 实例分析与仿真实验

3.1 BP网络结构设计

对于基于BP神经网络的矮小儿童智能诊断模型而言，神经网络的输入信息为影响儿童矮小的属性特征，总共有17个属性；神经网络的输出信息为最终诊断后的儿童矮小症的病因类型(如上文1.1所述)。考虑到基于BP祌经网络的矮小儿童智能诊断模型的输入变量和输出变量的规模较小，因此在这里选用一层隐含层即可满足网络的性能要求。通过试算法比较不同的隐层神经元数下网络的训练情况，最终设定隐含层数目为10。至此得到网络的拓扑结构为17 - 10 - 8，如图1所示。

3.2 模型重要参数的设置

在MATLAB的神经网络工具箱中，提供了多种不同的训练函数，在本网络中选择trainlm对网络进行训练，该函数的学习算法为Levenberg-Marquardt优化算法，其优点在于收敛速度很快，能够很好的达到预期的效率。选取purelin为神经元上的传递函数，误差界值设置为0.01。为了平衡速率与精度之间的关系，将学习率初步设置为0.1。

3.3 遗传算法对系统的优化设计

遗传算法[5]对系统的具体优化设计单元中，具体步骤如下：

(1) 初步确定BP神经网络连接的取值范围；

(2) 对网络连接的取值进行二进制编码；

(3) 以目标函数最大值作为遗传算法的适应度函数，即：

(10)

(4) 采用BP神经网络算法对所有权值组分别进行训练，如果该N组权值至少有一组满足精度的要求，那么寻优算法结束，不然就转入步骤(4)继续学习。

(5) 在训练好的N组较好的权值中随机选择N组新的权值，与原来N组权值组合在一起，构成一个完整的基因群体，这样就共得到2N组权值。

(6) 将这2N组权值进行遗传操作(复制、杂交、变异)。

(7) 对经过遗传操作后获得的新2N组权值进行排序，并从中选出N组较好的权值，跳转到步骤(3)。

遗传算法的优化[6]，首先需要设置一些具体的算法参数如：种群规模、迭代次数、交叉率、变异率等；其次要对每一个具体算子的内部参数进行相关设计和确定。采用实验数据与BP网络相同，30例样本数据的前20例用于训练，10例用于检测。根据网络模型的拓扑结构得到权值共有17×10+10×8=250个，阈值10+8=18个，遗传算法染色体编码长度[7]为250+18=268。确定好染色体编码长度后，对种群进行初始化，GA的编码程序可以实现初始化操作[8]，最后将遗传算法优化后的权值阈值传递给BP网络。

3.4 矮小儿童智能诊断的MATLAB仿真

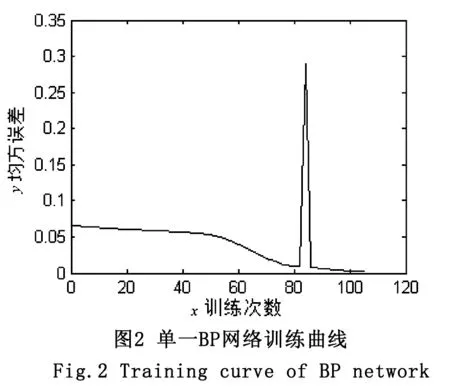
将实验数据用于单纯BP算法，网络的训练结果如图2所示。由实验仿真图可以看到，网络在训练到80次时达到期望的误差界值，但是仿真曲线显示在网络训练到大约82次时发生了振荡，这对实验结果的准确率产生一定影响。

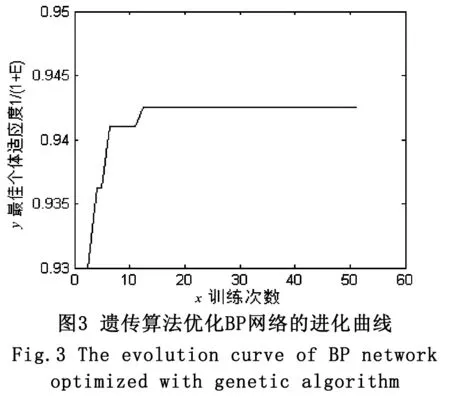
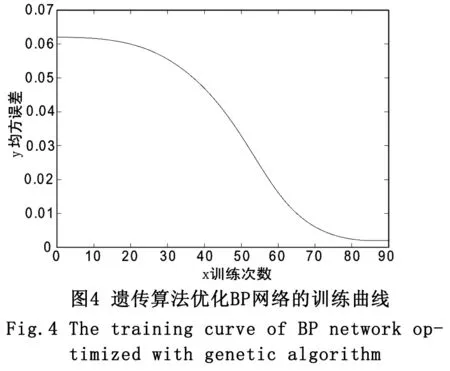
然后将相同的网络规模和拓扑结构运用到遗传算法的优化中，遗传算法优化BP网络的进化曲线如图3所示，优化算法的训练次数为50次，得出BP网络的平均收敛次数为85。遗传算法优化BP网络的训练曲线如图4所示，与传统BP网络相比，收敛明显加快，也没有发生训练振荡。

4 结论

(1)用遗传算法优化的BP网络和单纯的BP网络相比，无论是在收敛速度还是在训练的稳定性方面都表现出优势。

(2)将遗传算法与BP神经网络的结合充分发挥了遗传算法的全局搜索能力优势和BP神经网络的非线性映射能力和泛化能力的优势，提高了网络的性能，得到理想的实验效果，有效适用于对矮小儿童的智能诊断。

参考文献：

[1] 魏海坤. 神经网络结构设计的理论与方法[M]. 北京：国防工业出版社, 2005.

[2] 祁建勤, 凌 星, 李亚玲, 等. 矮小儿童发病因素临床分析[J]. 中国儿童保健杂志, 2006，14(1)：94-95.

[3] 王 华，胡学钢.医学数据挖掘中的数据预处理与Apriori算法改进[J]. 计算机系统与应用，2009，9(1)：94-97.

[4] P KAELO, M M ALI. Integrated crossover rules in real coded genetic algorithms[J]. European Journal of Operational Research, 2007, 7(6)：60-76.

[5] ZHEN GUOTU，YONG LU. A robust stochastic genetic algorithm for global numerical optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(5): 456-470.

[6] 王 南，张京军，高瑞贞. 基于改进遗传算法多体模型的汽车悬架参数优化[J].辽宁工程技术大学学报, 2007, 26(3)：435-437.

[7] 张京军，吕 品，高瑞贞，等. 单纯同伦算法的改进遗传算法 [J].辽宁工程技术大学学报, 2013，32(7):987-991.

[8] 熊 凌.基于遗传算法的BP网络全局收敛的混合智能学习算法[J].武汉科技大学学报, 2000，23(2):45-47.