三维蚁堆算法在视频关键帧提取中的应用

吴开兴, 沈志佳

(河北工程大学 信息与电气工程学院, 河北 邯郸 056038)

随着计算机的普及和网络技术的不断发展，越来越多的视频数据不断涌现。如何对这些数据进行高效的存储、浏览和检索便显得十分重要[1-2]。在基于内容的视频检索中，关键帧提取是最关键的技术之一。目前关键帧提取技术方法很多[3-10]，但多数存在提取效果不理想或算法复杂等问题。本文主要是在传统蚁堆算法的基础上，提出了一种改进的三维蚁堆算法，将传统算法的蚂蚁运动路径扩展到三维平面。则三维平面与三维视频帧特征向量的帧数一致，从而提高了聚类的查全率和查准率。

1传统的蚁堆算法

蚂蚁是一种社会性昆虫，具有自组织、自适应、分布式、相互通信、相互合作等特点。模拟蚂蚁的这些特性，我们可以解决许多很复杂的问题。Deneubourg等人从蚂蚁堆积尸体中受到启发，提出了一种基本模型BM(Basic Model)。Lumer和Faieta在BM的基础上进行了改进，增加了数据对象的相似性表达式，提出了用于数据聚类的LF算法。LF算法的基本思想如下：将N个数据对象随机的投入到M×M的网格中，将A只蚂蚁也随机的投入到该网格中，蚂蚁沿着网格随机移动，蚂蚁遇到数据对象后，根据该数据对象与蚂蚁可视范围内数据对象的相似度，以一定的概率负载数据对象，负载数据对象的蚂蚁沿着网格随机移动，当遇到空网格后，根据负载与可视范围内数据对象的相似度，以一定的概率卸载负载，然后未负载的蚂蚁继续随机移动。

设蚂蚁的可视范围为r，则相似度计算函数为如下公式[8]：

(1)

d(oi,oj)为数据对象oi与oj的距离，通常用欧式距离，a为相似性参数，neigh(r)表示以r为半径的圆形区域。

Pp和Pd分别为蚂蚁拾起对象和放下对象的概率，计算如公式(2)(3)[8]所示。

(2)

(3)

2 改进的蚁堆算法在关键帧提取中的应用

传统的蚁堆算法，是基于二维平面的，数据对象是以随机的方式投入到二维网格上。本文在传统蚁堆算法的基础上，将其扩展到三维平面，数据对象以其在H-S-V空间中的三维特征向量为坐标，分布在三维立体网格上。这样，数据对象之间的欧式距离，便是其在三维空间中的直线距离，距离近的数据对象聚集在一起，因此，数据对象已在一定程度完成了初始聚类。

首先进行视频帧特征向量的提取。视频帧的每个像素均可以在H-S-V空间中表现出来，其中H的取值范围为[0,360]，S和V的取值范围均为[0,1]，为了使视频帧的距离计算更加有效，将S和V的取值乘以360，使S和V的取值范围也扩展到[0,360]，这样就得到了关于每个象素的三维特征向量。计算第n帧整幅图像的平均特征向量Xn，两帧之间的欧式距离d(oi,oj)便可由公式(4)表示：

(4)

其中xnk为特征向量Xn的k维分量。

将每一个视频帧映射到三维的欧式空间，这样，两帧之间的欧式距离便可由三维空间中两点的直线距离表示。

一段镜头便可由三维空间中一系列的散点表示，如下图1。

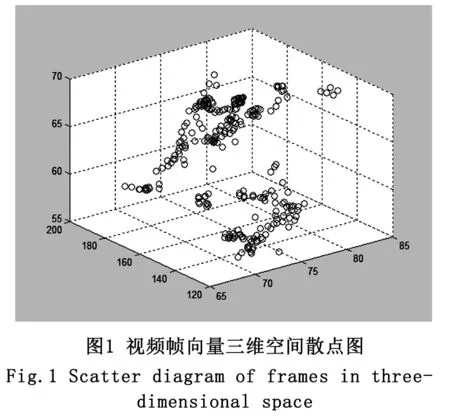
之后，我们通过对传统蚁堆算法进行改进，使其适应于H-S-V三维空间。具体的改进方面如下，

(1)将数据对象按照其在H-S-V中的坐标放在三维数据空间中，由于数据对象在三维空间中的实际距离，即是其欧式距离，从某种程度说，数据对象，已经完成了初始聚类。

(2)由于数据对象在三维空间中已经有一定的聚类性质，初始放置蚂蚁时，将蚂蚁均匀的分布在三维空间中，并且使每一只蚂蚁，在一个已有数据对象的网格内，避免蚂蚁对于负载的饥饿。

(3)数据对象周围的数据对象有很大几率属于同一聚类，因此，蚂蚁放下负载后，自动寻找与此数据对象最近的负载点，减少蚂蚁的无意义运动。

(4)蚂蚁拾起负载后，有很大概率，在其负载周围再次放下负载，因此，蚂蚁以负载初始位置为圆点，在半径r1为1的球面内运动，如果在此球面内不能放下负载，则半径r1+1，直到蚂蚁放下负载为止。此改进点的目的是使蚂蚁在较短的步数内，在正确位置放下负载，这也是因为数据对象之间的欧式距离就是其实际距离，欧式距离近的数据对象已经聚集在一起的缘故。

(5)如果蚂蚁欲放下负载的位置已有其它的数据对象，则在此位置的邻域内求其放下对象的概率。如果所有的领域都不能放下，则蚂蚁回到原先的运动路径，继续在以r1为半径的球面内移动。

(6)定义数据对象的优先级，如果，蚂蚁经过较少的步骤，即放下数据对象，说明数据对象已经在其正确位置，则此数据对象需要再次移动的概率很低，我们就赋予此数据对象较低的优先级，否则赋予较高的优先级，当条件一样时，即步骤3中存在多个最近负载点时，蚂蚁优先负载优先级较高的负载点，如果优先级一致则随机选取。

(7)参数a的确定非常依赖使用者的经验，使算法缺少普适性。算法中a初始值设为0.1，如果迭代时，蚂蚁放下对象失败次数与迭代次数的比值大于0.99，则a增加0.01，否则减少0.01。

(8)当蚁堆算法迭代到一定次数t后，数据对象已完成了进一步的聚类，按照文献[11]所述方法，再一次提取每一帧的H-S-V颜色直方图。之后以每一帧中H-S-V颜色直方图的72维特征向量为标准，以蚁堆算法提取的聚类中心和聚类个数作为参考，通过K-均值聚类算法完成最终的聚类。则最终聚类中，距离每一个最终聚类中心距离最小的维特征向量所代表的视频帧，即为我们所需要的关键帧。最终聚类选取72维颜色直方图作为特征向量是因为，采用72维特征向量，比前述三维特征向量在计算欧式距离时更精确，最终聚类的结果也会更准确。

3 实验结果与讨论

利用三维蚁堆算法提取出的基于前图1所代表镜头的关键帧如下图2所示。

可见提取出的关键帧分别代表了停车场某一个车位，汽车的动态变化，提取出的关键帧具有代表性。

利用本算法提取出的某个演讲镜头的关键帧如图3所示。

由于该演讲镜头内视频内容变化很少，所以仅提取出了唯一的关键帧，由此可见，本算法具有自适应性，能够根据镜头内容的复杂程度，自适应的提取出不同数量的关键帧。

为了验证算法的有效性，本文采用了120个不同的镜头来对算法进行分析。具体的实验结果如下图4、图5所示。

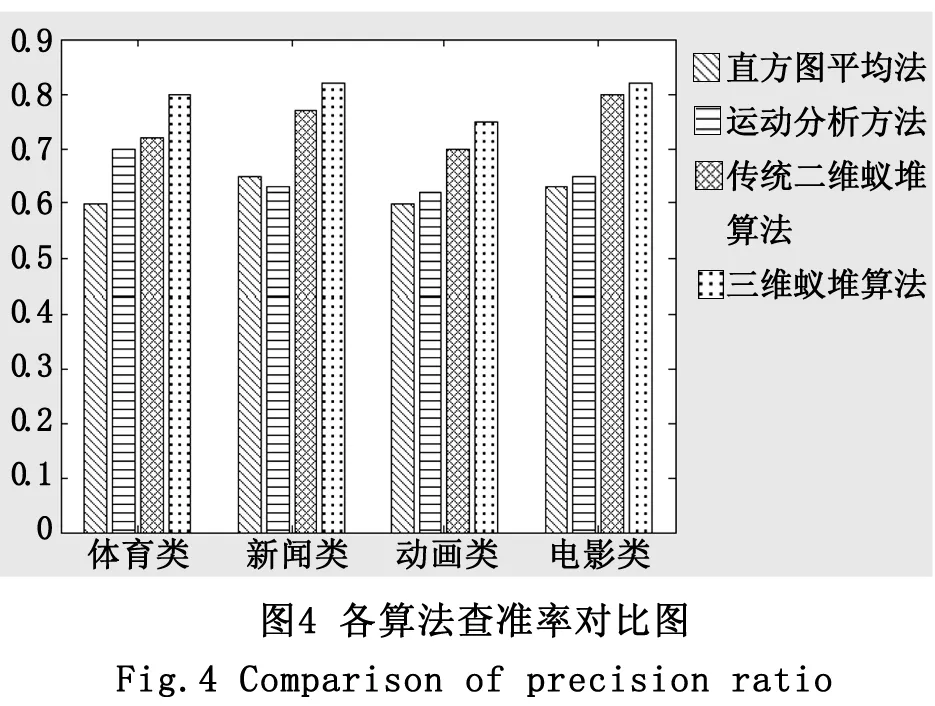
可见，无论是在体育类，新闻类，动画类，电影类的视频中，本文算法的查全率和查准率，都优于其它的传统算法。

4 结论

(1)本算法能够根据镜头内容的复杂程度，自适应地提取出不同数量，且具有代表性的关键帧。

(2)在体育类、新闻类、动画类、电影类的视频中，本文算法的查全率和查准率都优于传统的直方图法，运动分析法和二维蚁堆算法。

参考文献：

[1] TANIGUCHI Y. An intuitive and efficient access interface to real- time incoming video based on automatic indexing [C]// Proc of ACM Multimedia. San Francisco，1995: 25-33.

[2] 汪 勤. 基于视频图像处理的无人值守变电站在线检测的研究[J]. 四川理工学院学报: 自然科学版, 2013, 26(3): 91-94.

[3] 瞿 中, 高腾飞, 张庆庆.一种改进的视频关键帧提取算法研究[J]. 计算机科学, 2012(8): 300-303.

[4] 柴饶军, 马彩文. 图像序列中目标关键帧快速搜索算法[J]. 光子学报, 2004(10):1233-1235.

[5] WORF W. Key frame selection by motion analysis[C]//Proc of IEEE International Conference on Acoustics Speech and Signal Processing. Atlanta, 1996: 1228-1231．

[6] 顾家玉，覃团发，陈慧婷. 一种基于MPEG-7颜色特征和块运动信息的关键帧提取方法[J]. 广西大学学报: 自然科学版, 2010(2): 310-314.

[7] YANG SHUPING, LIN XINGGANG. Key frame extraction using unsupervised clustering based on a statistical model[J]. Tsinghua Science and Technology，2005(2): 169-173.

[8] HUA MAN, JIANG PENG. A feature weighed clustering based key-frames Extraction method[C]. // Proceedings of the 2009 International Forum on Information Technology and Applications. Piscataway，2009: 69-72.

[9] 张建明, 刘海燕, 孙淑敏. 改进的蚁群算法与凝聚相结合的关键帧提取[J]. 计算机工程与应用, 2013(3): 222-226.

[10] 贾存锋, 朱加雷, 焦向东, 等. GMAW熔滴过渡高速摄像系统与熔滴边缘提取[J]. 河北科技大学学报, 2013, 34(4): 316-319.

[11] 王 娟，孔 兵，贾巧丽，等. 基于颜色特征的图像检索技术[J]. 计算机系统应用, 2011(7):160-164.