电极型复电阻率扫频系统响应数值模拟

尹成芳, 柯式镇, 张雷洁

(1.中国石油大学, 北京 102249; 2.北京市地球探测与信息技术实验室, 北京 102249)

0 引 言

普通电阻率测井、电流聚焦测井、感应测井、电磁波传播测井、介电测井,以及阵列测井、井壁电成像测井、过套管电阻率测井等测井仪器所使用的测量频率和测量方式虽不尽相同,但它们大部分采用测量单一标量参数识别油气,没有同时采用多种参数及频谱特性参数识别油气,因而这些测井方法的测井响应的数值模拟计算相对简单。对于普通电阻率测井、电流聚焦测井视为稳定电场进行求解,对于感应测井、电磁波传播测井和介电测井则视为磁场问题进行求解。复电阻率测井[1-2]方法采用了2个频率的测量值,这种方法的数值模拟在已发表的文章[3-8]中虽然用到岩石复电阻率的频散特性给正演模型的介质赋于属性,但计算中均未考虑磁场影响,只求解标量电位的方程,因而只适用于频率不高的情况。对于多频率的应用,林树海等[9]采用多频电磁场法给出了模拟计算的结果,但其频率范围10～70 MHz,分布较窄,与传统方法相比没有较大优势。阵列感应测井虽然采用了多种频率进行测量,但只是为了寻求匹配相应仪器长度探测深度所需的频率[10],没有用于直接识别油气。斯伦贝谢公司的介电扫描测井所用频率20 MHz～1 GHz,范围属于射频-高频范围,受趋肤效应明显,探测深度较浅(2.54～10.26 cm)[11],基本在冲洗带范围内。本文在岩石物理性质实验研究[12-15]的基础上提出一种采用电极方式进行复电阻率扫频的测井方法,并采用同时考虑标量电位势和矢量磁势的有限元算法进行仪器响应模拟计算,从而进行电极系的优化设计、探测特性及测井响应的考察,为仪器的实现进行论证和指导。

1 复电阻率扫频电测井原理

电极型复电阻率扫频电测井仪器采用如图1所示的电极系作为探测器。其尺寸参数描述为

整个探测器全长6.12 m;电极系具有3个探测深度,对应于3种工作模式(见表1);测量频率为10 Hz～500 kHz,取若干个频率点进行测量(如100 Hz、30、100、200、300 kHz和500 kHz等6个频率)。测量参数有A0电极电流、M1电极电位等。对于每个频率,测量A0电极的供电电流和复电压,并计算出地层复电阻率

(1)

式中,UA0为A0电极处测得的复电压;IA0为A0电极电流,当以电流为参考相位时为标量。

当测量完所给的多个频率下的电阻率值后,用Cole-Cole电阻率频散模型[16]拟合得到地层的电频谱曲线,利用该频谱曲线可以计算出多种与地层含水饱和度相关参数,因而可以用来识别油气。

图1 复电阻率扫频电极型电测井探测器示意图

工作模式电极工作情况模式1屏蔽电极A1(或A1')供屏流;UM1=UM2;A2(或A2')、A3(或A3')作为回路电极接地模式2屏蔽电极A1(或A1')、A2(或A2')供屏流;UM1=UM2;A3(或A3')作为回路电极接地模式3屏蔽电极A1(或A1')、A2(或A2')、A3(或A3')供屏流;UM1=UM2;远电极作为回路电极接地

2 数值模拟方法

10 Hz～500 kHz频率范围的复电阻率扫频测井其电磁场问题可以由Maxwell方程组描述

(2)

式中,E为电场强度;B为磁场强度;D为电通密度;H为磁通密度;Je为介质中的涡流密度;Js为电流源提供的电流密度;ρ为电荷密度。

状态方程为

D=εE,Je=σE,B=μH

(3)

由以上方程及B=A和E=-可得涡流区域

(

(4)

(5)

非涡流区域

(A)=μJs

(6)

根据变分原理由式(4)、式(5)、式(6)可得矩阵方程

(7)

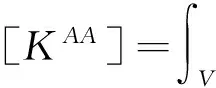
根据有限元原理离散并求解上述矩阵方程可以求得各节点的矢量磁位A和标量电位φ,然后根据式(1)计算出地层复电阻率。

3 算法实现与计算实例

根据上述算法在ANSYS平台[17-18]上实现了电极型复电阻率扫频测井响应数值模拟计算。①选择电磁功能模块及耦合场单元SOLID236。②进入预处理阶段,根据仪器参数建立有限元模型及介质模型,通常是圆柱体。所建介质模型半径30 m、高度40 m。③对所建的计算模型进行网格剖分和属性赋值。网格采用变尺度自动划分,由内到外依次变大。根据岩心实验数据(见图2)拟合得到Cole-Cole模型各参数,给介质属性赋值。④边界条件约束和激励加载。边界条件约束主要是无穷远边界施加矢量磁位和标量电位为0。激励加载则是将电流强度加到发射电极上。⑤方程组求解。给定分析类型和加载的信号频率,选择求解器求解。⑥处理。根据计算结果输出的参数,计算仪器测量信号,完成整个数值模拟计算过程。

图2 岩心实验测得的岩石电频谱响应

3.1 算法正确性验证

为验证算法的正确性,用该算法计算典型三层介质模型(目的层电阻率为666 Ω·m,围岩为63 Ω·m,层厚1 m)、100 Hz的测井曲线与采用直接求解标量电位的拉普拉斯方程法(用SOLID231单元计算)得到的计算结果进行比较(结果见图3),二者具有很好的一致性,二者最大误差不超过0.3%,说明了采用耦合方程的计算方法正确可行。

图3 典型三层介质模型2种不同算法计算的测井曲线对比

3.2 无限大均匀介质电频谱响应

考虑涡流影响时计算得到仪器的地层电频谱响应如图4和图5所示。由计算结果可见,在这种情况下虽然存在明显的涡流影响,但其频谱特性依然能被监测到。当把式(4)中的涡流项去掉后再进行模拟计算,其结果如图6和图7所示。涡流的影响没有了,地层的电频谱非常清楚地被监测出。由此可见,用这种方法再加上合适的涡流影响校正方法完全可以很好地探测到地层电频谱特性。

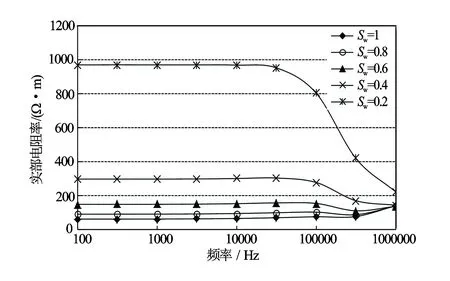
图4 考虑涡流影响计算的地层电频谱响应实分量

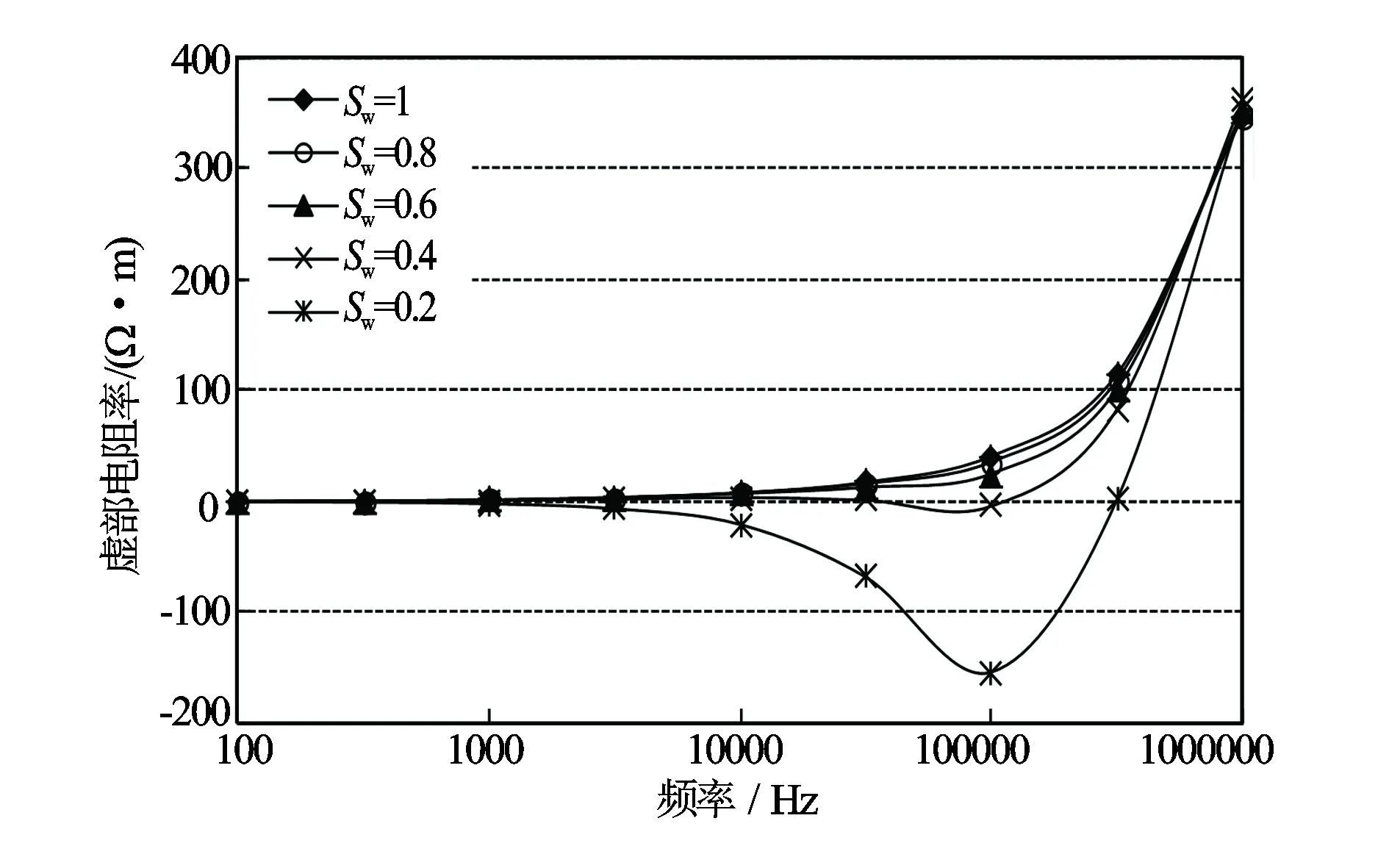
图5 考虑涡流影响计算的地层电频谱响应虚分量

图6 不考虑涡流影响计算的地层电频谱响应实分量

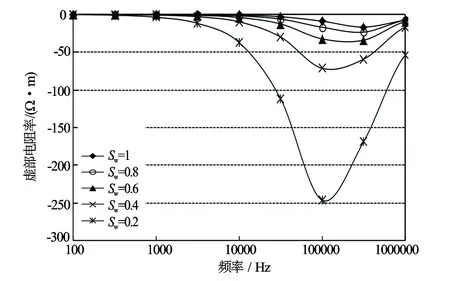
图7 不考虑涡流影响计算的地层电频谱响应虚分量

3.3 仪器的径向探测特性考察

由于多频测量要求不同频率的探测深度要尽量一致,所以对仪器探测深度有较高要求,在电极系设计时必须进行计算考察。首先计算3个不同探测深度在相对低(1 kHz)和高(100 kHz)的频率径向探测深度(计算结果见图8和图9)。由结果可见,在这2个频率,3个工作模式仪器径向探测深度明显分开,很好地实现了浅、中、深的探测特性,而且从1～100 kHz探测特性变化不大。对于深探测工作模式,计算出不同频率仪器径向探测深度如图10所示,计算结果可以进一步证明频率从10 Hz到1 MHz范围内变化,仪器的径向探测特性变化不大,说明了采用电极作为探头的复电阻率扫频测井探测器是合适的。

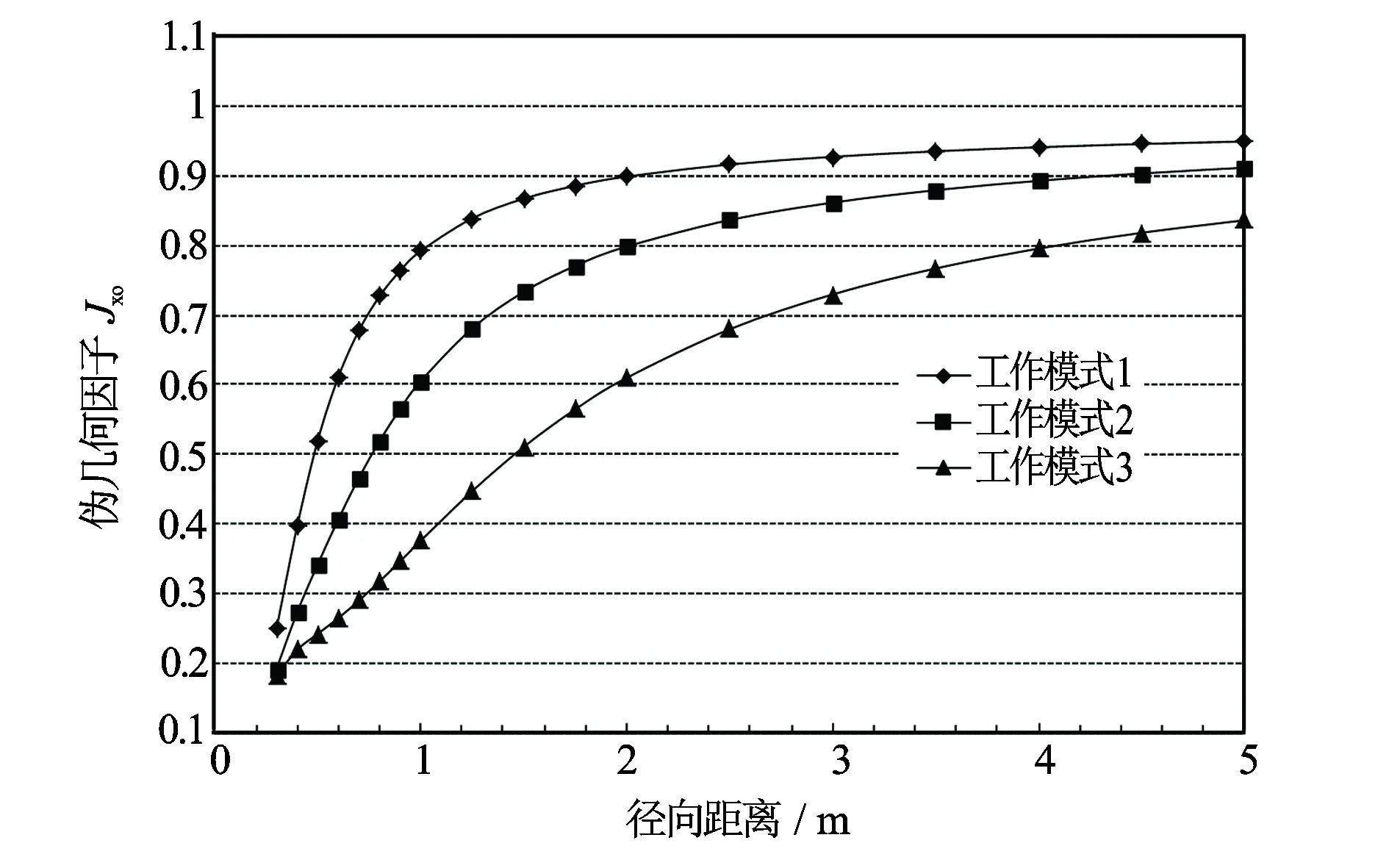
图8 频率为1 kHz时的3个不同工作模式径向探测特性曲线

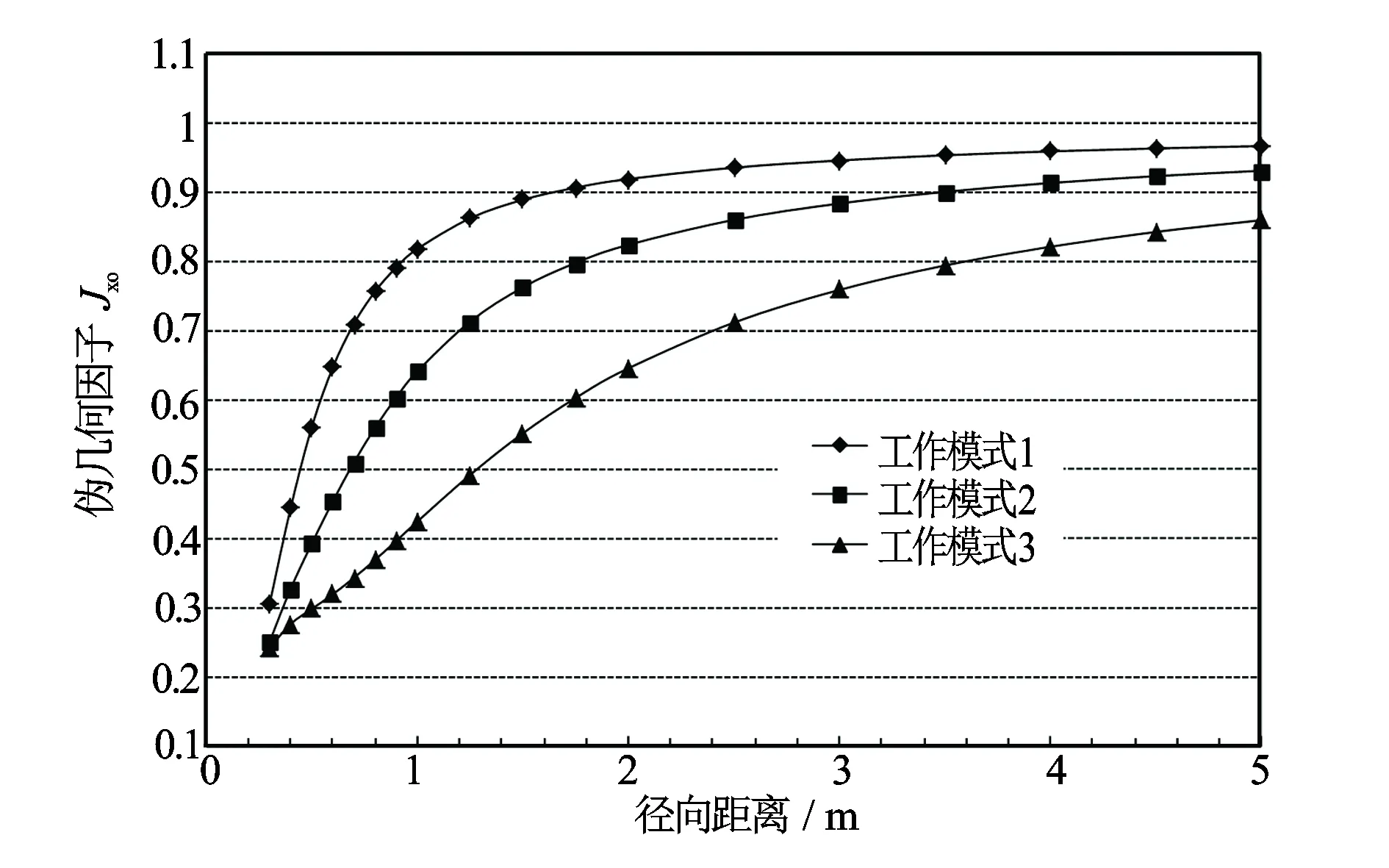
图9 频率为100 kHz时的3个不同工作模式径向探测特性曲线

3.4 典型三层介质下的测井曲线

为考察仪器过地层界面的响应特性,计算了典型三层介质模型(带井眼,围岩100%含水,目的层25%含水,无侵入)的测井曲线。计算结果如图11和图12所示。由结果可以看出仪器的地层界面响应平稳,各个频率对油气层均有响应,而且不同频率对油气层的响应程度不同。根据实验室测量结果分析,虚部电阻率界面极化频率与含水饱和度存在近线性关系(见图13)。该特性预示识别油气将突破传统单一电阻率或单一介电常数识别油气的方法。

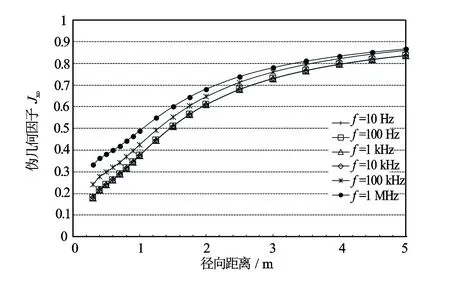
图10 不同频率深探测径向探测特性曲线

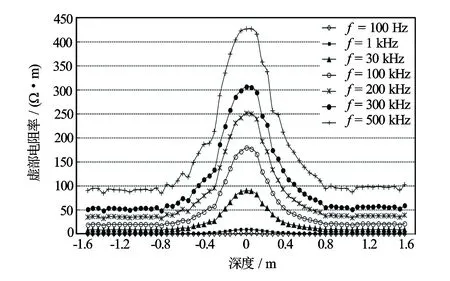
图12 典型三层介质模型复电阻率扫频测井曲线虚部电阻率响应

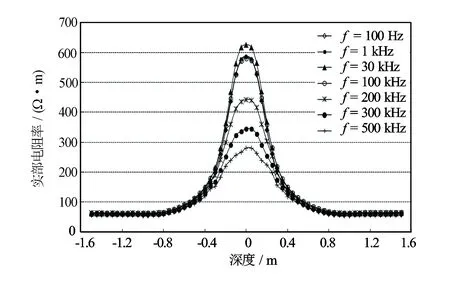
图11 典型三层介质模型复电阻率扫频测井曲线实部电阻率响应

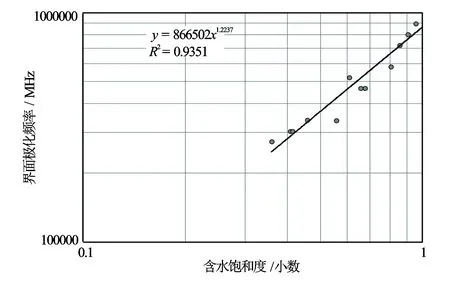
图13 界面极化频率与含水饱和度交会图

3.5 平衡监督电极M1和M2电极相位差随频率的变化

探测器选用了平衡监督电极M1和M2的电位平衡条件,它们之间的相位不一致将影响这一条件的成立,在测量频率范围内必须考察这2个监督电极的相位差及其随频率的变化情况。针对不同含水饱和度计算M1和M2的2个电极的相位差随频率的变化关系见图14。可以看出,频率不同相位差是不同的,但差值均很小,最大值不超过0.1 °,可忽略不计,说明探测器的平衡控制没问题。

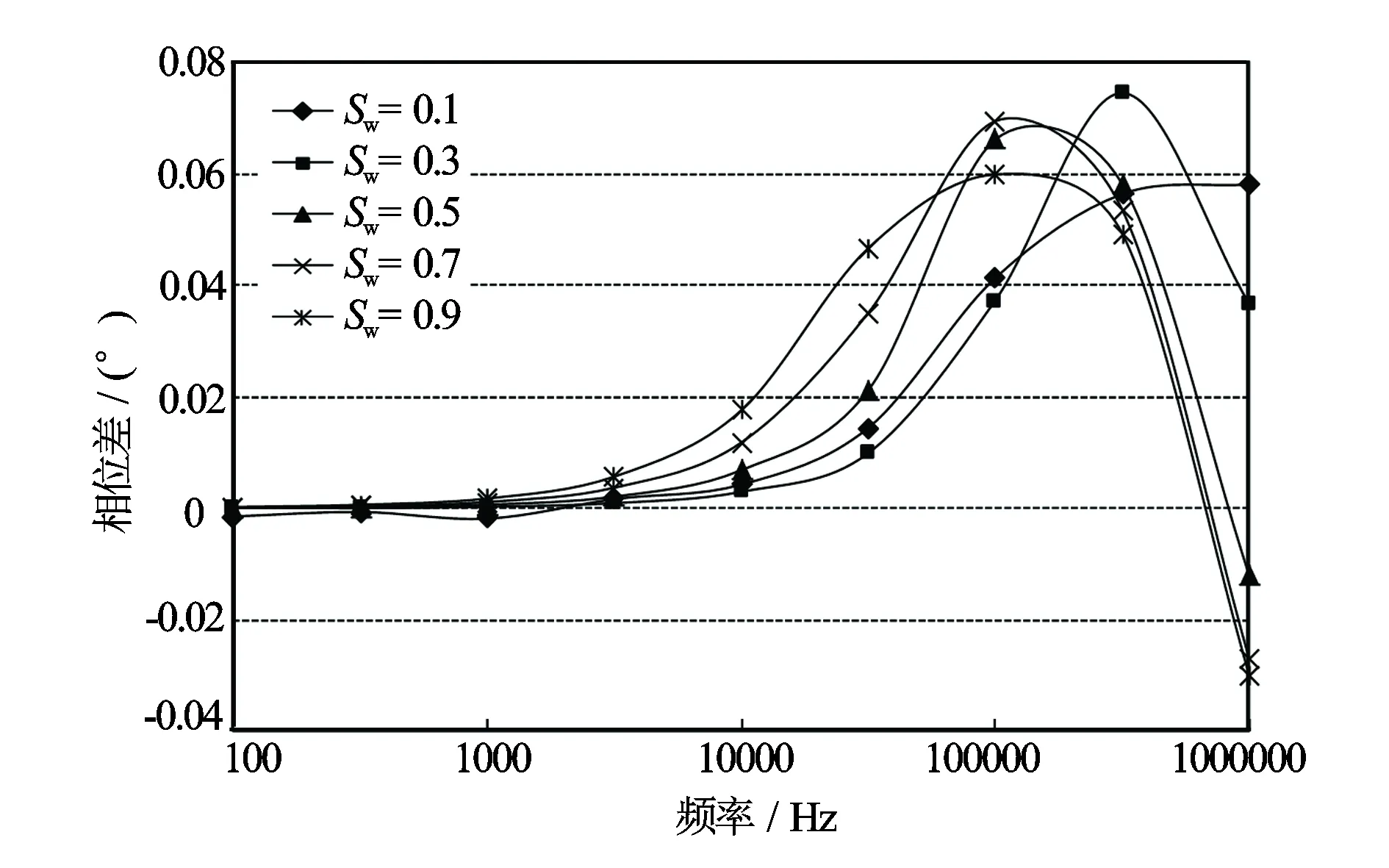
图14 探测器监督电极M1和M2之间相位差随频率的变化关系

4 结 论

(1) 利用ANSYS平台可以进行标量电位和矢量磁位耦合计算,可以模拟计算电极型复电阻率扫频测井仪器响应。

(2) 复电阻率扫频测井方法探测到地层的电频谱特性,可以识别油气。

(3) 所设计的探测器径向探测深度随频率变化不大,且最大探测深度达1 m以上,满足了多频测量需要。

(4) 在测量频率范围内,2个监督电极的相位差随频率而变化,但其变化最大值不超过0.1 °,对仪器平衡控制的影响可以忽略。

参考文献:

[1] 陈序三, 赵文杰, 朱留方. 复电阻率测井方法及其应用 [J]. 测井技术, 2001, 25(5): 327-331.

[2] 柯式镇, 冯启宁, 何亿成, 等. 电极法复电阻率测井研究 [J]. 石油学报, 2006, 27(2): 89-92.

[3] 柯式镇, 何亿成, 邓友明, 等. 复电阻率测井响应的数值模拟 [J]. 测井技术, 2002, 16(6): 446-448.

[4] 杨韡. 双侧向型复电阻率测井响应的数值模拟 [J]. 地震地质, 2005, 27(3): 412-418.

[5] 肖占山, 徐世浙, 罗延钟, 等. 复电阻率测井的数值模拟研究 [J]. 石油地球物理勘探, 2007, 42(3): 343-347.

[6] 杨晓弘, 何继善, 孝忠. 频率域激电有限元数值模拟 [J]. 地球物理学进展, 2008, 23(4): 1186-1189.

[7] 蔡军涛, 阮百尧, 赵国泽, 等. 复电阻率法二维有限元数值模拟 [J]. 地球物理学报, 2007, 50(6): 1869-1876.

[8] 李勇, 林品荣, 李桐林, 等. 基于异常复电位2.5维CR有限元数值模拟 [J]. 吉林大学学报: 地球科学版, 2011, 41(5): 1596-1604.

[9] 林树海, 佟文琪. 多频电磁波测井的数值模拟 [J]. 长春科技大学学报, 1998, 28(4): 458-463.

[10] Hunka J F, Barber T D, Rosthal R A, et al. A New Resistivity Measurement System for Deep Formation Imaging and High-resolution Formation Evaluation [C]∥SPE 00020559, 1990.

[11] Mehdi Hizem, Henri Budan, Benoit Deville, et al. Dielectric Dispersion: A New Wireline Petrophysical Measurement [C]∥SPE 116130, 2008.

[12] 范宜仁, 陆介明, 王光海, 等. 岩石电阻率频散现象的实验研究 [J]. 石油大学学报, 1994, 18(1): 17-23.

[13] 郑和华, 冯启宁, 尚作源. 岩石复电阻的频率特性及其应用前景 [J]. 石油大学学报, 1993, 17(增刊): 23-28.

[14] 柯式镇, 冯启宁, 孙艳茹. 岩石复电阻率频散模型及其参数的获取方法 [J]. 测井技术, 1999, 23(6): 416-418.

[15] 苏庆新, 柯式镇, 冯启宁, 等. 100Hz～10MHz频段含油水两相岩石电阻抗的研究 [J]. 地球物理学进展, 1999, 14(1): 93-103.

[16] Pelton W H, Ward S H, Hallof P G, et al. Mineral Discrimination and Removal of Inductive Coupling with Multi-frequency IP [J]. Geophysics, 1978, 43(5): 588-609.

[17] 安世亚太公司. ANSYS低频电磁场分析指南 [Z]. 2012.

[18] 安世亚太公司. ANSYS高级分析指南 [Z]. 2012.