浅谈经济研究中的数学模型
2014-05-07杨鸿雁
●杨鸿雁
纯粹的量的关系和形式是数学研究的主要对象,将具体形象的实际内容舍弃,只保留一般的数量关系,关注其抽象的共性,是数学研究的特征;反之,经济学及其他学科最为感兴趣的是自己所抽象的公式(数学模型)能否说明某一现象、解决相应的问题以及其使用的约束条件如何,这样矛盾自然也同时存在两者之间。然而在经济领域中用数学方法能够很好说明某些现象或概括某些问题却是不争的事实,因此在经济学中使用数学的关键问题仅仅在于其实践性或适用性方面①。建立数学模型能够研究变量之间的关系,探究事务变化的规律,用可控变量计算出必要的结论,进而总结出理论假说,这便是数学模式在经济研究领域中的运用。如今经济学已经成为了一门高度数学化的社会科学类学科,数学成为经济模型建立和推导的主要工具,很多数学的重大研究已经运用于经济学理论中。现在这两者矛盾争论的焦点不再是经济学需不需要使用数学方法,而是怎样在经济研究中使用数学方法的问题。虽然现代经济学在研究经济问题方面已经获得了较好的成效,但是对于经济学而言某些数学模式是否能够运用其中,或者如何更好地运用其研究经济问题仍需要进一步探究。
一、数学模型的基本内涵
数学模型是采用有关数学思想,对数学研究中的各种问题的一种整体概述和表述。其一般是为了解决数学问题,对某个特定对象提出必要的条件和假设,使用数学图形、数学关系式、图表等数学专业术语以及合理的数学方法和手段获取的数学结构。这种数学结构的形式丰富多彩,其能够是一种算法语言,可以是一个数学图表,也可以是几种结构的混合。将数学领域的具体问题抽象和简化为数学模型即是数学建模,其包含提出问题、简化问题、模型建立、模型验证、模型修改、模型使用等多方面内容②。
在经济研究中引进数学工具进行解析,把复杂的经济问题用精练的数学语言予以表达,从而把经济中相互影响的因素建立起具有逻辑性的相互联系,然后通过计算找出其内在的规律性及其具体数量,这样的数学表达式(函数式)就称为经济模型,或经济的数学模型。
二、数学经济建模及其重要性
数学经济建模是对客观经济现象进行总体概述,并采用模型方式体现各种经济现象中各个要素间的相互数量关系,是经济研究中比较重要的方法。其本质就是把错综复杂的实际经济问题用数字、字母和其他数学符号形成的不等式、或等式以及图像、图表、框图等数学语言简化、抽象为合理的数学结构的过程。应用数学去解决各类实际经济问题时,建立数学经济模型是十分关键的一步,同时也是十分困难的一步。无论是建立数学经济模型,还是运用模型对有关经济问题进行定量研究分析,都需要丰富的数学知识,比如数学中的线性代数、数学分析、常微分方程、概率论、数理统计、模糊数学等知识就必不可少。然而纵观现代发展史得知,经济发展的速度与数学经济建模具有紧密的联系。在经济决策定量化、科学化呼声越来越高涨的今天,数学经济建模已经广泛运用于各个经济活动之中。比如,汉森、希克斯两位经济学家用IS—LM模型对凯恩斯的有效需求理论进行了较为完善的阐述,不仅如此,凯恩斯主义的经济政策即财政政策和货币政策的分析,也是圈绕IS—LM模型而展开的。因此,IS—LM模型是凯恩斯主义宏观经济学的核心,是数学和经济学有机结合的经典之作。再比如,在实际生产、营销中,生产商可以按照客户提出的产品质量、数量、交货期、交付地点、交付方式等需求,运用快速报价系统(按照生产商各种资源、生产成本、产品生产流程以及客户要求等数据建立数学经济模型)与客户进行直接交流和沟通。
三、构建经济数学模型的方法和步骤
数学模型广泛运用在经济研究领域中,包括政策评价、经济预测、结构分析等多方面。经济政策评价包括理论分析和实践分析两个方面。理论分析包括研究分析、评价政策的效果,并对不合理的部分进行修改补充,以更加符合经济规律的要求。实践分析主要是分析政策所产生的政治的、经济的、社会的实际效果,并对原政策方案进行检验、修改、完善。在进行政策目标评价时,通过对相互矛盾的目标进行综合分析,制定出这些目标在一定条件下能相互协调的宏观经济政策和微观经济政策,其使用的研究分析方法有IS—LM模型、脉冲响应函数、方差分解等;经济预测是在对一定时期的客观经济活动过程进行深入调查的基础上,运用各种科学的方法,对掌握的经济信息加以分析研究后,并评估和预测未来经济活动发展状况及变化趋势,其使用的研究分析方法有时间数列法、指标分析法、因素分析法等;结构分析是经济研究的重要内容,它是对经济现象中各种变量之间的关系进行全面研究,是当一个变量或几个变量出现变化时,是否会对其他变量以及经济体系产生影响所进行研究分析。其使用的研究分析方法有乘数分析、弹性分析以及比较静力分析等。
一般而言,针对经济研究问题,建立一个科学合理的数学模型主要包括以下步骤:(1)全方位了解各种实际问题和与问题相关的其他各种知识;(2)按照研究的目标和任务,针对研究的现象进行全方位、多层次的调查研究,尽可能获得更多的数据信息,并对各项数据进行正确分组;(3)把研究的实际问题进行抽象、简化,确定模型中各种影响因素,并分析出重要因素,使用参数和数量来表达这些因素。采用数学知识来描绘问题中变量参数之间的联系,初步形成数学关系式③;(4)进一步简化、合并数学关系,最后构建成数学模型;(5)运用总结分析得出的数据,使用有关数学方式计算出所建立的模型中参数的估计值,进而明确模型;(6)偏差分析所确定的模型阐述,将模型结论与实际测量数据进行对比分析,以验证模型是否跟实际问题相符合。如果相差甚远,就必须进一步调整修改模型,在按照以上程序再进行一次,直到构建完成的模型符合实际问题。
四、数学模型在经济研究中的应用举例
本文以弹性分析和线性规划为例,体现数学建模在经济研究过程中的重大作用。
案例1:弹性分析模型。弹性是一个数学概念,为相对变化率,即是相互依存的一个变量对另外一个变量变化所表现出来的反应程度。

弹性的数学含义是自变量变化1%所引起因变量变化的百分数。由比例学分析得知,弹性是一种不借助其他任何单位的计量方法,即是无量纲的。把弹性理论用于经济研究领域,能够为经济研究提供有效的方法。需求价格弹性就是数学弹性分析模型运用于经济研究中具体体现。
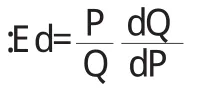

比如:假定某产品的需求函数为Q=3000e-0.02p,问价格为100时的需求弹性,分析其经济内涵。

经济含义为:当价格是100元时,如果价格提升1%,则需求量将会降低2%。进一步讲,因弹性系数大于1,即需求量的变化率大于价格的变化率,故需求量对于价格的变化率是比较敏感的,也称需求富有弹性或高弹性。
案例2:0-1线性规划模型。它是为解决实际优化问题的所谓分派一类问题而产生的,下面举例说明其数学模型是如何建立的。
某企业计划招收m个岗位,人力资源管理部门需要从n个应聘者中招收m个工作人员(n≥m)。企业规定每个岗位只需要一名工作人员,工作人员只需要专职做一件工作,通过测试,第i个工作人员做j件工作的效率为Cij,问应该招收哪些人员,怎样分配工作才能获得最佳的效益。
解答:设xij=1代表第i个应聘人员只做第j件工作,xij=0代表第 i个应聘人员不做第 j件工作(i=1,2,3.....;j=1,2,3,.....),然后其线性规划模型为:

上述模型中,由于决策变量取值只是0或者1,因此该模型为0—1规划,是整数规划的特例。
此外,数学模型运用到经济研究过程中的案例较多,比如运用概率分布构建预期收益模型、运用微分方程构建经济增长模型、运用微积分构建最优化价格模型、利用期望值法解决a风险型决策问题、运用Shapley值法建立收益合理分配模型等。
随着经济研究越来越深入,采用数学工具来分析和解释经济问题已经成为了经济领域研究最重要的方法。尤其是最近几年来,计算机技术发展尤为迅速,开发了很多数学运用软件,利用数学模型来解决复杂的经济问题变得尤为高效,同时也提高了分析和解决经济问题的准确性和真实性,为社会经济的发展做出了较大的贡献。
注释:
①张丽莉.关于跨学科研究方法的启示——数学模型在经济学中的应用[J].信息系统工程.2012,11(02):100-102
②刘旭东.引领探究过程 建构策略模型——浅谈数学建模思想在“倒推”教学中的应用[J].课程教育研究,2014,1(03):45-46
③兰亮.一类灰色平衡数学模型的研究及其在陕西经济协调发展研究中的应用[D].西安建筑科技大学,2008
