模糊物元模型在区域粮食安全评价中的应用

2014-05-07陈兆荣雷勋平

重庆文理学院学报（社会科学版） 2014年2期

陈兆荣，雷勋平，2，王亮，叶松

近度复合模糊物元RρH，根据贴近度值对粮食安全状况进行优劣排序.

20世纪70年代，联合国粮农组织提出粮食安全概念:“粮食安全是保证任何人在任何时候都能得到为了生存和健康所需要的足够食品.”［1］粮食安全关系到国民经济发展大计，我国政府历来都重视粮食安全问题，2013年中央经济工作会议把“切实保障国家粮食安全”放在2014年经济工作的六大主要任务之首，提出了“以我为主，立足国内，确保产能，适度进口，科技支撑”的国家粮食安全战略.因此，粮食安全评价有助于掌握粮食安全风险状况，有助于揭示粮食安全的内在规律，有助于化解影响粮食安全的潜在风险要素，为有效进行科学决策提供理论依据.从现有文献看，关于粮食安全评价主要有粮食安全指数法［2，3］、主成分分析法［4］、层次分析法［5］、改进熵值法［6］、突变级数法［7］和神经网络法［8］等综合评价方法.这些评价方法考虑问题的侧重点不尽相同，导致评价结果也不尽相同，且存在一定的不足:①粮食安全指数法侧重于评价粮食安全的某一方面，不能综合反映区域粮食安全的整体状况;②层次分析法的评价结果容易受评价专家主观上的不确定性及认识上的模糊性影响;③主成分分析法、改进熵值法、突变级数法和神经网络法皆计算过程繁琐，且要求满足较大的样本量等条件.

模糊物元模型是将模糊数学和物元理论相结合的分析方法，用来解决具有模糊性、不相容性问题.该模型理论简捷，方法简便，可操作性强，无需进行复杂的数学运算就可以得到较为可靠的评价结果，提高了评价方法的实用性.本文以中部地区6省粮食安全为例，运用模糊物元模型对区域粮食安全进行研究，探讨该方法在区域粮食安全评价中的有效性.

1 评价指标体系构建及评价方法

1.1 粮食安全评价指标体系

影响粮食安全的要素不仅包括耕地资源、农业生产投入、自然灾害、粮食零售价格和生产资料价格等因素，还包括物价水平、人口增长等消费需求因素［9］.在参阅其它文献［2，5，10-13］的基础上，课题组构建区域粮食安全评价指标体系(表1)，资料来源参考文献［14］.

表1 粮食安全评价指标体系

1.2 评价方法

1.2.1 模糊物元模型

设事物N，其关于特征C的量值为V，现以R=(N，C，V)来描述事物的基本元，称为物元［15］．如果量值V存在模糊性，那么物元R称为模糊物元，记作式中:N为事物;C为事物M的特征;μ(x)为与事物特征C对应的模糊量值，表示事物N对其特征C相应量值x的隶属度．

若有m个事物及其n个特征C1，C2，…，Cn，以及相应的模糊量值，称为m个事物的n维模糊复合物元［16］，记作 Rmn，即

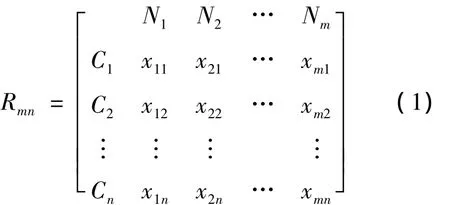
Rmn为m个事物的n个模糊特征的复合物元;Nj为第 j个事物(j=1，2，…，m);Ci为第 i个特征(i=1，2，…，n);xji为第j个事物第 i个特征对应的模糊量值.

1.2.2 从优隶属度模糊物元

从优隶属度是指各单项指标从属于标准方案评价指标的模糊隶属程度，根据评价指标特征根对应方案评价的优劣，可以分为正向指标和逆向指标，分别采用不同的计量公式计算从优隶属度，形式如下:

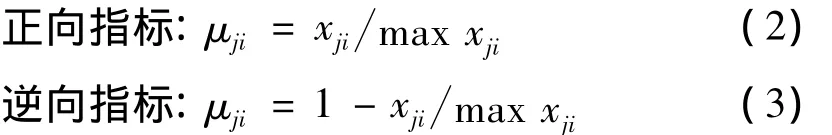
其中，μji为从优隶属度，max xji为第j个评价指标中的最大值.这样构造出复合从优隶属度矩阵¯Rmn.

1.2.3 标准模糊物元与差平方复合模糊物元

从优隶属度矩阵¯Rmn中各评价指标的从优隶属度的最大值或最小值被称为标准模糊物元R0n，如果最大值表示最优，则各指标从优隶属度均为1．若以Δji(j=1，2，…，m;i=1，2，…，n)表示标准模糊物元R0n与复合从优隶属度模糊物元¯Rmn中各项差的平方，则组成差平方复合模糊物元 RΔ，即 Δji=(μ0j- μji)2，可表示为:

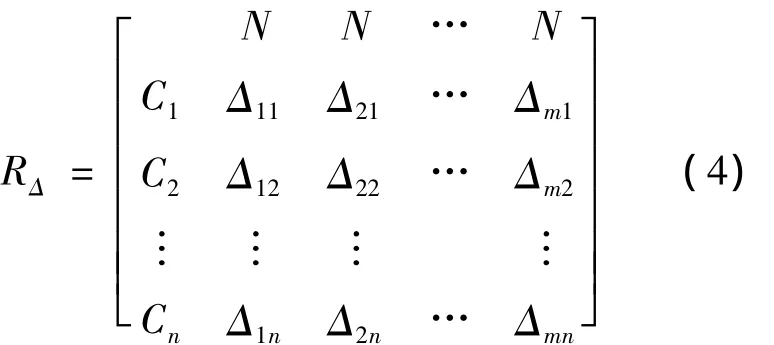
1.2.4 熵值法确定权重系数

熵值法确定评价指标权重是根据指标信息熵提供的信息.信息熵小表示该指标提供的信息量大，则该指标被赋予的权重大;反之，信息熵大表示该指标提供的信息量小，该指标应赋予较小的权重.权重计算步骤如下:

(1)指标无量纲化处理.

建立m个对象n个指标的判断矩阵(xji)m×n，j=1，2，…，m;i=1，2，…，n．采用阈值法对判断矩阵原始数据进行处理，公式如下:

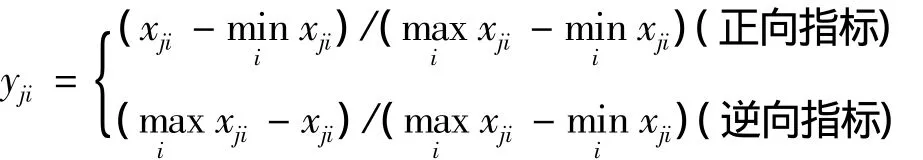
本课程共有12名教师，全部为双师素质教师，专兼职各占50%，形成了学历、学缘、年龄结构合理的教学梯队。课程负责人是本校护理专业负责人，教学实践经验丰富，教研科研成果丰硕。

(2)将各指标同度量化，计算第i项指标下第j个地区指标值比重

(3)计算第 i项指标的熵值 ei=-，其中ei为指标熵值，k为大于零的正数，设定k=1ln(n )，确保0≤ ei≤1．

(4)计算第i项指标的差异性系数gi=1-ei熵值越小，指标间差异系数越大，指标就越重要.

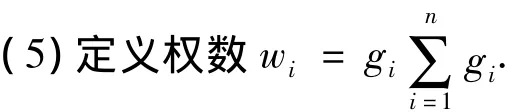
1.2.5 贴近度和综合评价

贴近度反映的是被评价样本与标准样本之间接近的程度，其值的大小往往能够反映出两者的接近程度，通常贴近度越大，则两者越接近;反之，则相差越大.因此，可以通过计算贴近度的大小来对各待评对象进行优劣排序.这里采用先乘后加运算欧氏贴近度 ρHj，则 ρHj=1-;从而可以构造欧氏贴

近度复合模糊物元RρH，根据贴近度值对粮食安全状况进行优劣排序.

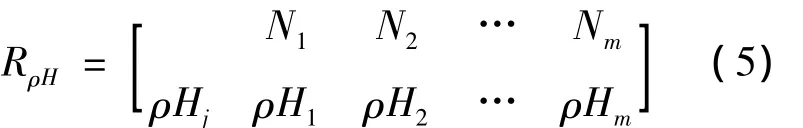
2 模糊物元模型在粮食安全评价中的应用

利用模糊物元模型对中部地区6省2010年粮食安全状况进行评价.中部地区包括山西省、安徽省、江西省、河南省、湖北省和湖南省等6省，该地区总人口为35 672.51万(2010年)，占全国总人口的26﹪;农用地面积为8 032.9万hm2，占全国农用地面积的12.22﹪;耕地面积为28 993千hm2，占全国耕地面积的23.82﹪.该地区是我国重要的粮食主产区，全国13个粮食主产区省份中部地区占有5席，2010年该地区粮食产量16 720.7万 t，占全国粮食总产量的30.6﹪，其在全国粮食生产与供应体系中具有重要地位.同时，由于该地区人地矛盾比较尖锐，水旱等灾害频发，导致粮食生产具有一定的波动性.这种波动性给我国的粮食安全造成很大的隐患.因此，对该地区的粮食安全进行评价具有一定的理论意义和实用价值.参照既定的粮食安全指标体系，收集中部地区6省的粮食安全指标数据(表2)，数据来源于参考文献［14］.

表2 中部6省2010年粮食安全评价指标数据

步骤1:构造复合物元．由公式(1)将表2中的中部地区6省视为物元的事物，可以构造由6个事物与其相应的15个评价指标及其属性值的复合物元．

步骤3:计算标准模糊物元和确定差平方复合模糊物元．标准模糊物元R0，15是由步骤2所确定的复合模糊物元R6．15内各评价样本从优隶属度中的最大值或最小值加以确定的．这里，选取最大值组成标准模糊物元，也就是各指标从优隶属度均为1．

根据公式(4)计算标准模糊物元 R0，15与复合模糊物元R6．15中相应各项差的平方Δij=(μ0j-μij)2，再由计算所得的Δij，组成差平方复合模糊物元 RΔ，即

步骤4:确定评价指标权重.采用熵值法，计算出熵值得分作为权重，见表3.

表3 评价指标权重

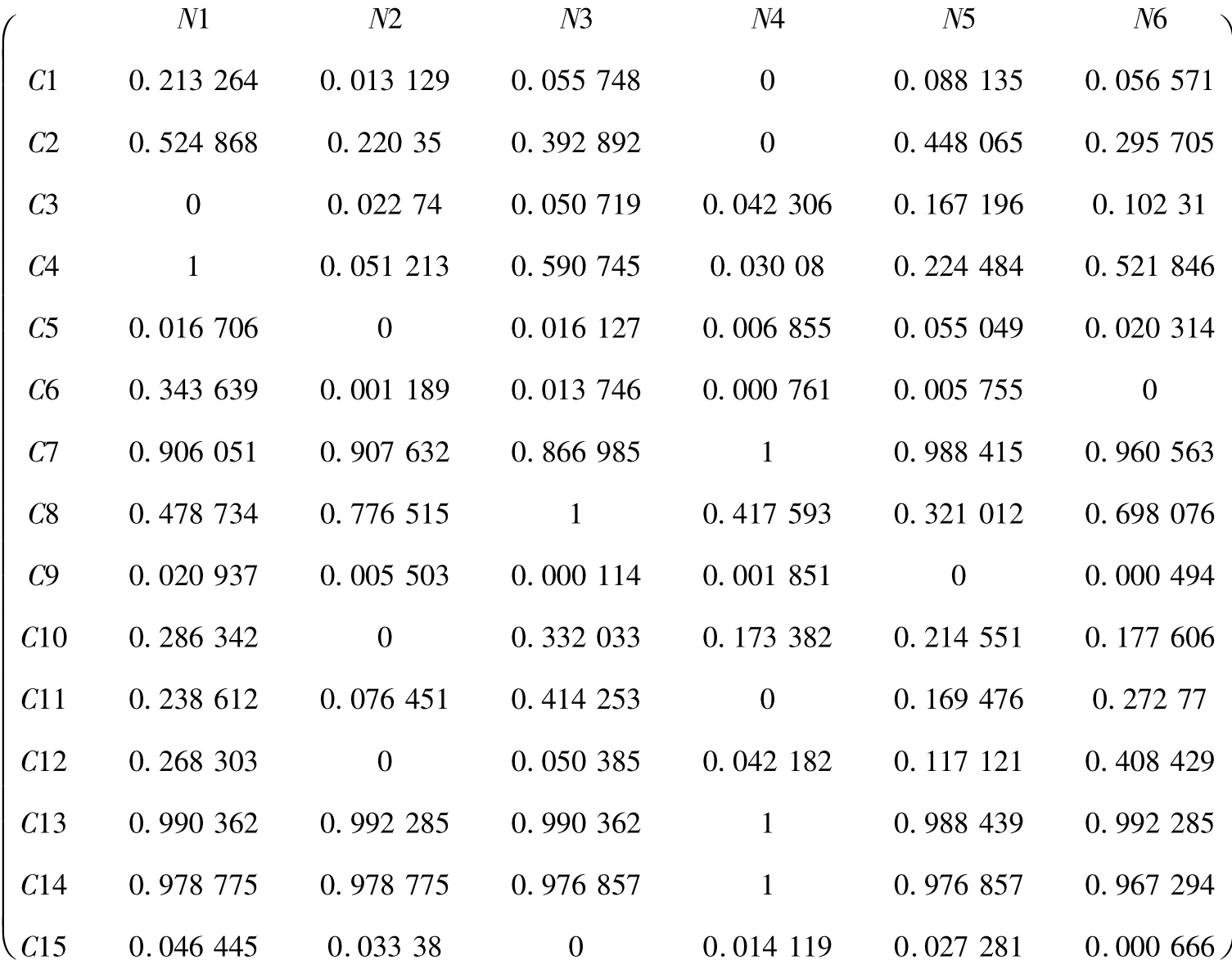
步骤5:贴近度计算.由差平方复合模糊物元RΔ和评价指标权重W，根据公式(5)可以得到评价样本与标准样本之间的贴近度ρHj，如表4所示.

表4 欧氏贴近度复合模糊物元

评价结果的分析:从表4结果可以看出，在待评的6个省份中，贴近度最大值为0.763 616，最小值为0.304 404.中部地区粮食安全状况由优到劣的排序依次为:河南省＞安徽省＞湖南省＞江西省＞湖北省＞山西省.河南省粮食安全程度最高，山西省粮食安全最低.2010年中部地区6省粮食产量分别为山西省1 085.1万t、安徽省3 080.5万t、江西省1 954.7万t、河南省5 437.1万t、湖北省2 315.8万 t和湖南省2 847.5万 t，其中江西、湖南2省因灾害粮食产量有所减少.基于模糊物元模型的评价结果与该地区粮食产量有较强的相关性，说明这种方法在区域粮食安全评价中具有一定的可行性和科学性.

3 结论

本文基于区域粮食安全概念的模糊性和单项指标评价结果的不相容性，在物元分析的基础上，以模糊集理论结合物元分析，建立区域粮食安全的模糊物元评价模型，利用该模型对中国中部地区6省粮食安全状况进行优劣排序，为区域社会经济协调发展和粮食安全提供决策依据.应用实例表明:该模型概念清楚，计算过程简单，且熵权的引入有效地增加了评价结果的客观性，易于计算，能有效地评价区域粮食安全状况.该评价方法具有可操作性，评价结论与现实情况基本相符，具有一定的理论推广和实用价值.

［1］胡红帆.联合国粮农组织粮食安全特殊计划［J］.世界农业，2000(2)：3-5.

［2］马九杰，张象枢，顾海兵.粮食安全衡量及预警指标体系研究［J］.管理世界，2001(1)：154-162.

［3］尹惠斌.湖南省粮食安全评价及影响因素分析［J］.湖南财政经济学院学报，2012，28(136)：75-80.

［4］周庆元.基于主成分分析的粮食安全评价研究［J］.兰州学刊，2010(8)：43-45.

［5］刘凌.基于AHP的粮食安全评价指标体系研究［J］.生产力研究，2007(9)：58-60.

［6］谢小兵，金彦平.基于改进熵值法的我国粮食安全测度与评价［J］.新疆农垦经济，2012(4)：1-4.

［7］赵黎明，张亚兰.突变级数法的中心城市粮食安全绩效评价［J］.天津大学学报：社会科学版，2010，12(4)：304-307.

［8］吴声怡.应用神经网络评价粮食安全［J］.福建论坛，2002(3)：39-41.

［9］黄季焜.新时期国家粮食安全战略和政策的思考［J］.农业经济问题，2012(3)：4-8.

［10］朱泽.中国粮食安全问题：实证研究与政策选择［M］.武汉：湖北科学技术出版社，1998.

［11］农村社会经济调查司.我国粮食安全评价指标体系研究［J］.统计研究，2005(8)：3-9.

［12］张少杰，杨学利.基于可持续发展的中国粮食安全评价体系构建［J］.理论与改革，2010(2)：82-84.