基于热—机耦合的大轴重车轮踏面制动热负荷仿真分析*
2014-05-04常崇义
李 兰,常崇义
(中国铁道科学研究院 铁道科学技术研究发展中心,北京100081)
热—机耦合的联合方程可写成:
我国重载货运列车正朝着快速大轴重的方向发展。在货车提速、轴重增加以后,列车的动能急剧增加,制动时所产生的热量也大大增加。我国的重载列车主要采用车轮踏面制动的形式,在紧急制动停车时,由动能转换成的热能几乎全部被摩擦副所吸收。高摩合成闸瓦是重载及提速货车配套制动技术之一,由于合成闸瓦导热性差,因此使用合成闸瓦同采用铸铁闸瓦时相比,车轮在制动过程中要吸收更多的热量,从而更易受到热损伤。2003年王京波使用MARC有限元软件建立快速货车车轮二维有限元模型,采用数值和试验方法对合成闸瓦对车轮的热影响进行了研究[1]。2006年西南交通大学刘俊红采用三维模型分析了重载车轮的温度场和应力场[2]。但以往的这些车轮热负荷计算初始条件都在25 t轴重以下,一般也没有考虑热载荷和机械载荷相互作用的影响。近年来的实践表明,随着轴重及速度的提高,车轮由于制动产生损伤的比例大大增加。在货物列车提速到120 km/h,轴重从现在的25 t增加到27 t,甚至32.5 t时,紧急制动工况下,在规定的制动距离内停车,所产生的制动热负荷能否满足车轮不失效的要求,以及对车轮安全性的影响是急需研究和解决的问题。
1 车轮踏面制动的热—机耦合有限元理论
在车轮踏面制动时,车轮的温度场和热应力场属于两种不同性质的物理场,相关的计算涉及到对这两种物理场的耦合。耦合分析方法分为直接耦合法和间接耦合法。传统的热—机分析采用间接耦合分析方法,对于结构或物体先进行热传导分析,然后将热传导的结果作为边界条件再进行应力分析,这种分析无法考虑结构变形和应力分布对热传导的影响,以及瞬态温度对结构材料的影响。车轮踏面在制动过程中,车轮产生变形的同时还伴随着温度的变化。准确分析温度和应力变化不应把温度场的求解和应力场的分析分解开来,因为除了温度变化对结构变形和材料性质产生影响外,结构变形也会反过来改变热边界条件,进而影响温度变化。温度与位移两种不同场变量之间存在很强的相互作用[3]。完全的热—机耦合有限元模型则可以考虑结构变形和应力分布对热传导的影响,以及瞬态温度对结构材料的影响。
对于热弹性变形的材料本构关系为

其中,θ=T-T0,T为当前绝对温度,T0为初始绝对温度。
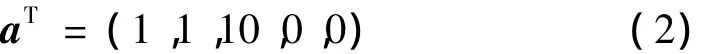
θ代表了温度变化;D为弹性常数;ε为应变常数。
β为温度应力模量。

E为材料的杨氏模量;a为热膨胀系数;γ为泊桑比。
热传导的基本能量平衡方程为
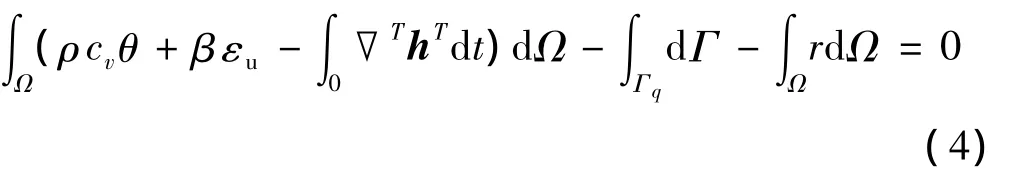
其中,cv比热容,q是物体边界面上法向的热流密度,r为物体内部的热源密度。
通过物体的热流密度(通过单位面积的热流量)是由傅里叶定律控制

其中k为热传导系数;h为热流密度。
Tβεu为热—机耦合过程的机械能,在传统的热—机非耦合分析中被忽略。温度变化θ<<T0,在式(4)中T0近似T,可以得到足够的精度。
假如边界点被绝缘或者被指定某一温度,δθ是允许温度,它们满足相容性所要求的连续性条件和温度边界条件。
在有限元方法中,运动xi(X,t)近似的表示为
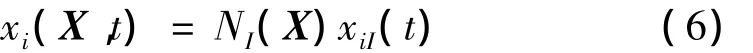
温度变化θ近似的表示为
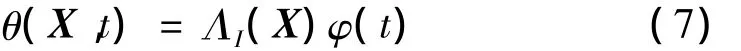
式中,NI(X)和ΛI(X)为形函数;xiI为节点I位置坐标;位移场可表示为
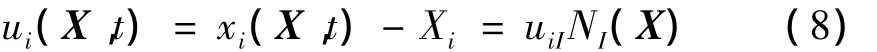
应变为
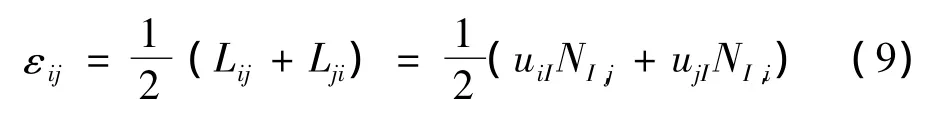
结构位移变分后得到
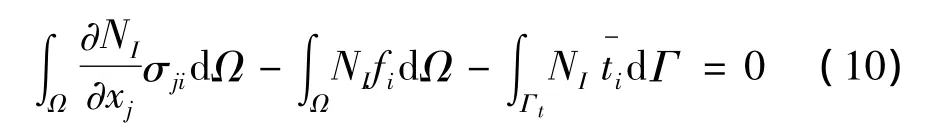
根据式(1),可得

其中
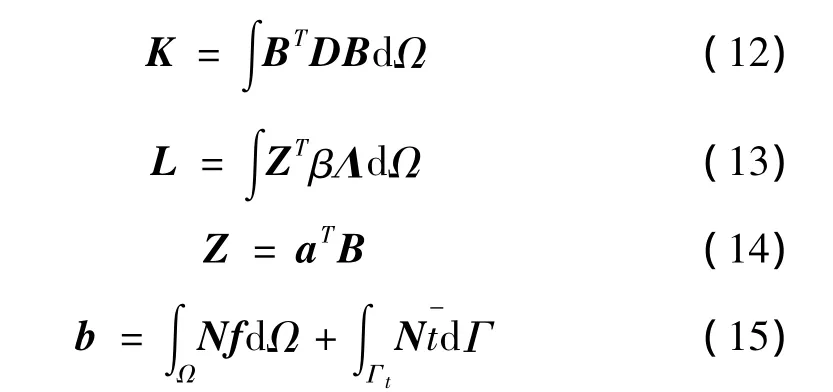
B为应变矩阵
根据式(2)变分后可得
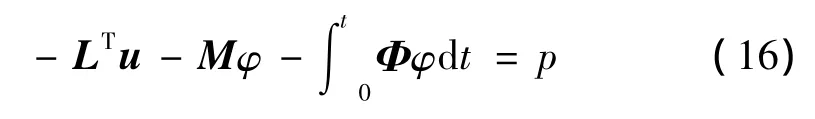
其中
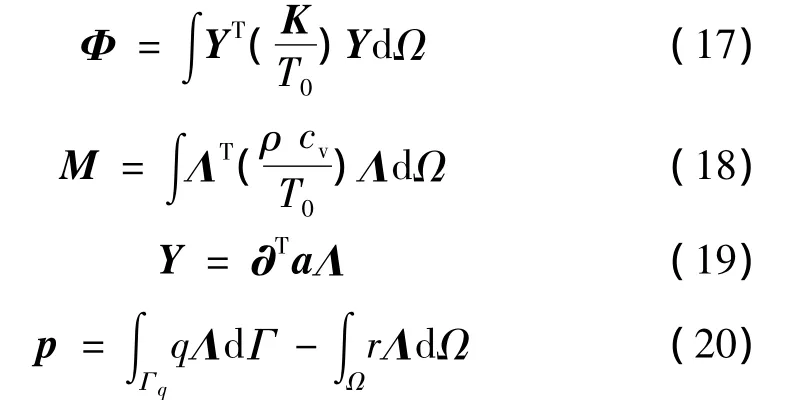
式(11)和式(16)为热—机耦合的离散平衡方程。
热—机耦合的联合方程可写成:
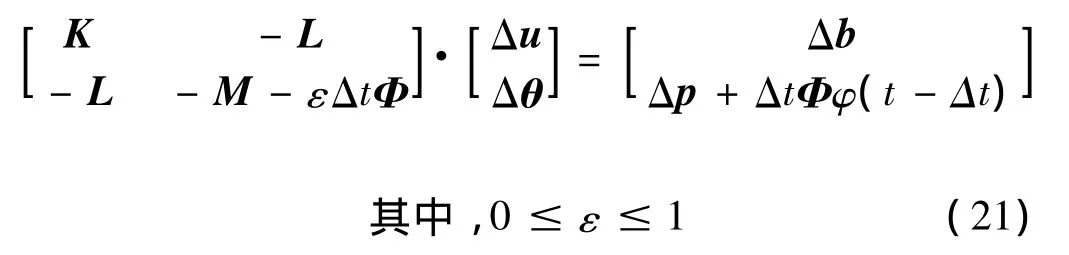
这里采用更新拉格朗日方法求解热—机耦合问题。即在每个增量开始时将几何形状更新,在新的拉格朗日坐标下分析温度场方程。采用非线性方程迭代解法求解热传导方程的等效温度场递推关系式,在同一时间增量步中,更新温度值,更新材料力学性质和热应变,迭代求解力平衡方程,收敛后,进行下一增量步的分析直到所需的增量步结束。方程组(21)中热传导方程是关于时间的一阶微分方程,通常采用后差分方案对其进行积分。
2 车轮踏面制动热—机耦合计算边界条件
车轮在制动过程中的温度场分布由两方面因素决定:一是从摩擦表面生成的热量通过车轮踏面传给车轮。这包括踏面和闸瓦由摩擦生成的热输入和轮轨接触蠕滑所产生的热输入;二是车轮中的热量又通过对流和辐射等方式传给周围的空气等介质,如图1所示。相对于由闸瓦和踏面之间的剧烈摩擦生热而言,无论是从热输入的大小来看,还是从热输入的冲击性来看,轮轨接触蠕滑生热都要小得多,因此可以忽略由轮轨接触蠕滑生成的热输入,而只考虑制动过程中闸瓦和踏面之间摩擦产生的热输入。
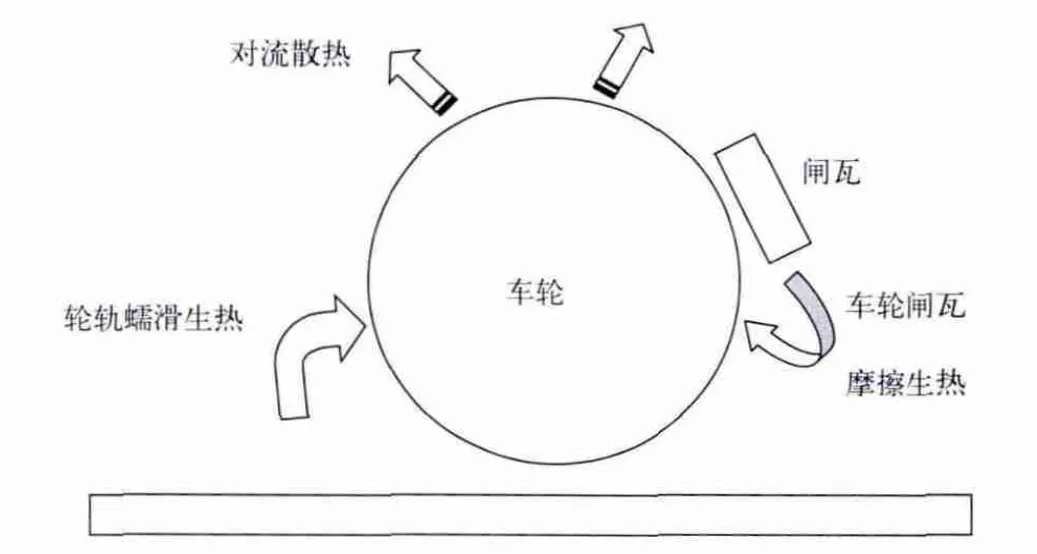
图1 车轮制动过程中的热量传输情况
初始条件整个模型的初始温度为已知值。第2类边界条件热流密度采用摩擦功率法计算。假设踏面与闸瓦接触的各个部分各个点的热流密度相同,呈均匀分布,当闸瓦在踏面上滑动时,则热流密度:
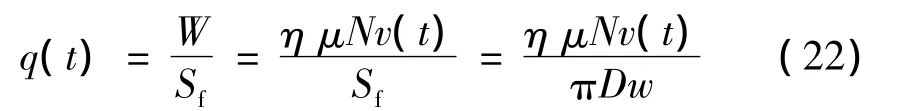
式中η为热流分配系数;F为滑动摩擦力;μ为摩擦系数;N为闸瓦压力;v(t)为车轮和闸瓦的相对滑动速度;W为摩擦表面的摩擦功率;sf为车轮旋转一周闸瓦在踏面上扫过的面积。
第3类边界条件对流换热系数取决于流体流动状态、流体物理性质、壁面温度以及壁面的几何形状,依据文献[4],可将踏面制动时车轮表面与周围空气间的热交换看成是圆柱扰流问题,表示如下:

空气的热物理性质参数值取 λ=3.21×10-2W/(m·K),γ0=2.313 ×10-5m2/s,Pr=0.688。
辐射换热系数表示为:
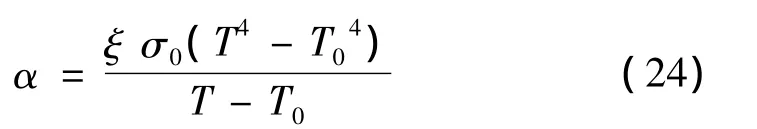
式中T为车轮表面温度,K;T0环境温度,K;ξ为车轮表面黑度,查阅手册取ξ=0.3;σ0为斯蒂芬—波尔兹曼常数,σ0=5.67 ×10-8W·m-2·K-4。
3 重载车轮制动热—机耦合计算模型及试验验证
计算模型选用的车轮为我国重载S型辐板车轮,轮径为840 mm,踏面为LM型踏面。利用有限元软件ABAQUS建立了车轮二维轴对称模型,单元采用轴对称CAX4RT单元,有限元模型如图2和图3所示。踏面制动闸瓦为高摩合成闸瓦,闸瓦型号为HGM-A,闸瓦的设计宽度为85 mm。车轮与车轴材料参数如表1所示。

图2 重载车轮踏面制动的热—机耦合有限元模型
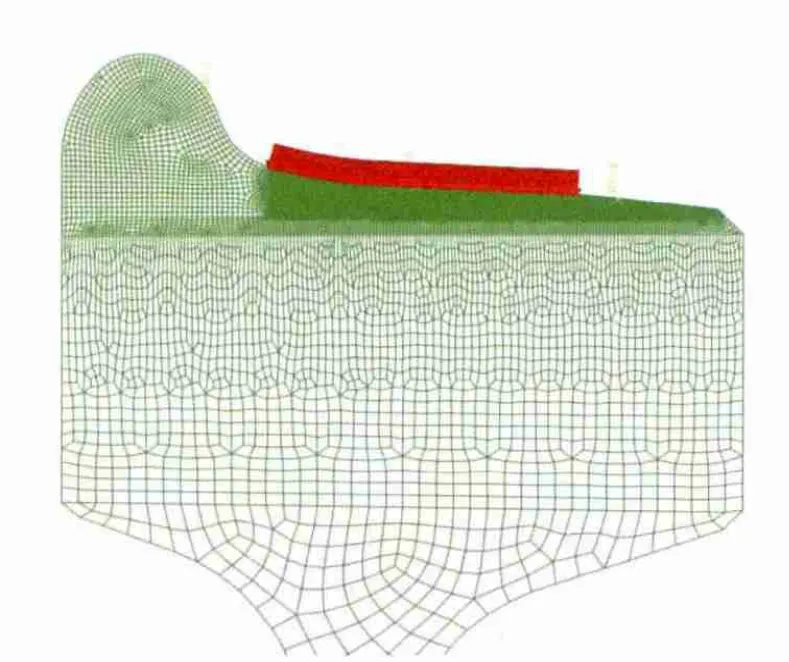
图3 局部放大的有限元网格
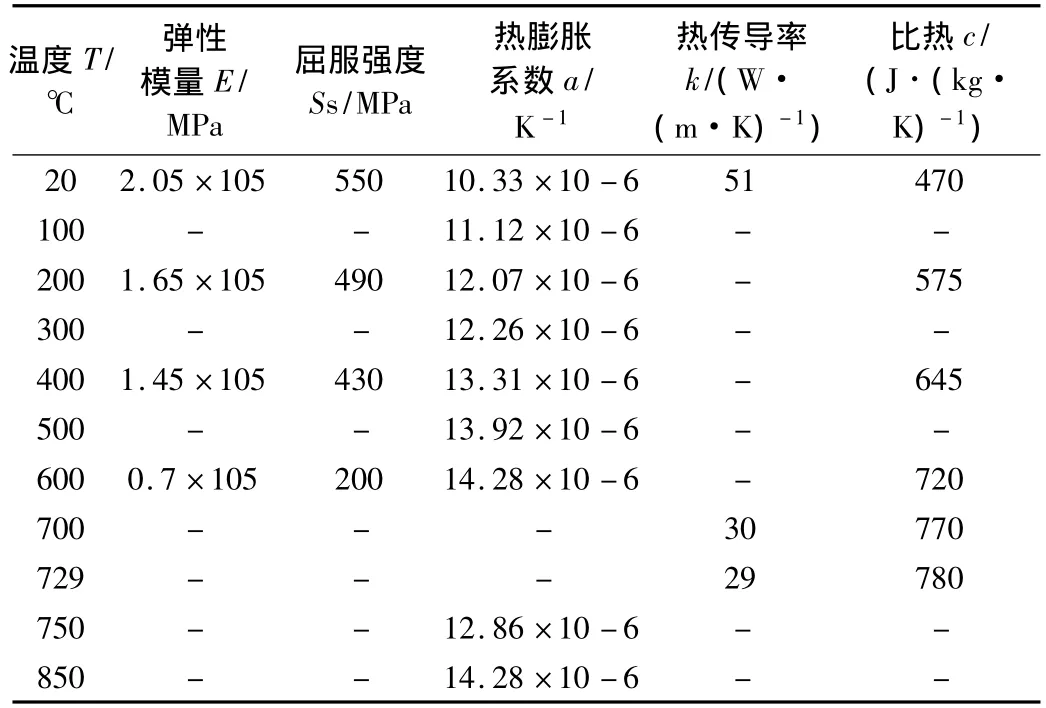
表1 车轮、车轴材料参数
重载货车车轮制动热负荷试验在中国铁道科学研究院制动试验室进行,如图4所示。试验工况为轴重23.7 t,闸瓦压力 19.6 kN,制动初速度 120 km/h,车轮和闸瓦的平均摩擦系数为0.318,踏面初始温度50℃。经统计,制动试验台的制动时间分布平均值为59 s,试验台用红外测温仪测得制动出现的最高温度分布平均值为 414.6℃。

图4 货车车轮闸瓦制动热负荷试验
热—机耦合有限元模型施加载荷和边界条件后,进行瞬态的热—机耦合分析,紧急制动计算从制动开始到制动全过程,计算结果得出紧急制动工况下踏面温度随时间的变化规律及应力随时间的变化规律如图5所示。从图中看出在25 s时,温度达到最高410.3℃,接近试验的平均值414.6℃,整个过程的制动时间为61 s和试验非常接近,在6.6 s时出现了最大圆周应力和Mises应力,它们分别是 -530.4 MPa 和467.9 MPa。
踏面出现最高温度时的温度场分布如图6所示,在出现最高温度时,圆周方向的应力分布和Mises应力分布如图7所示。车轮出现了最大圆周应力和Mises应力主要由于车轮内部温度分布梯度较大造成的,这种温度分布如图8所示。
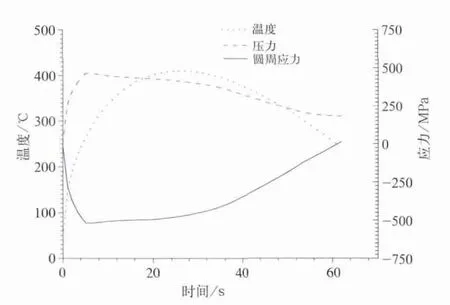
图5 踏面随时间变化的最高温度变化曲线及应力变化曲线
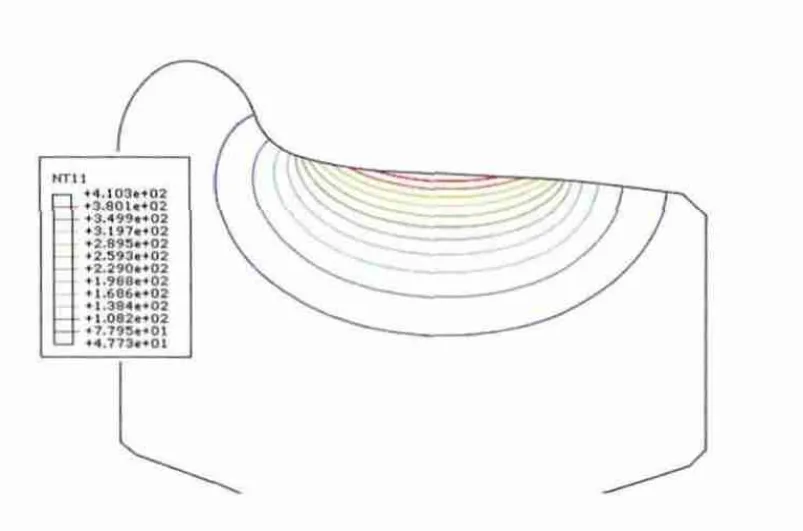
图6 踏面出现最高温度时的温度场分布图
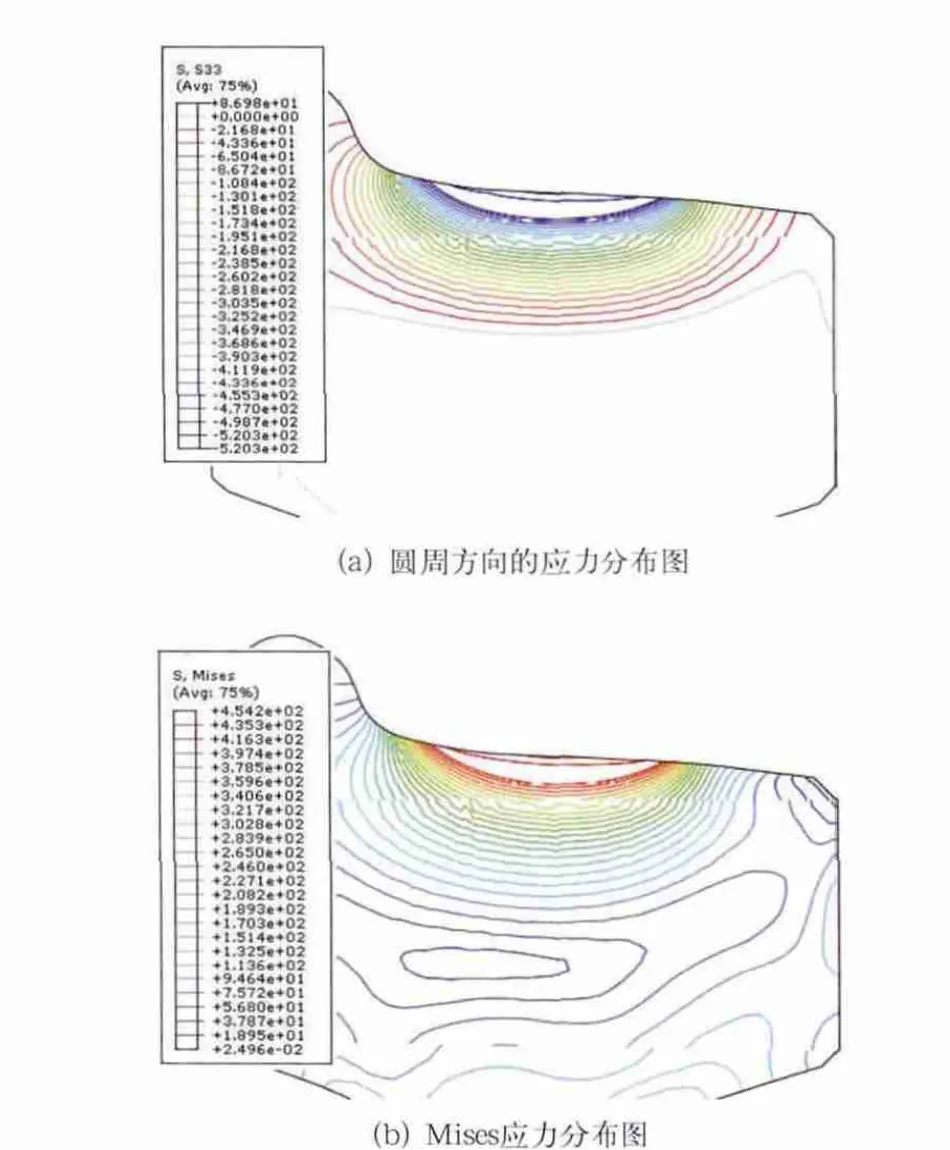
图7 踏面出现最高温度时的应力分布图
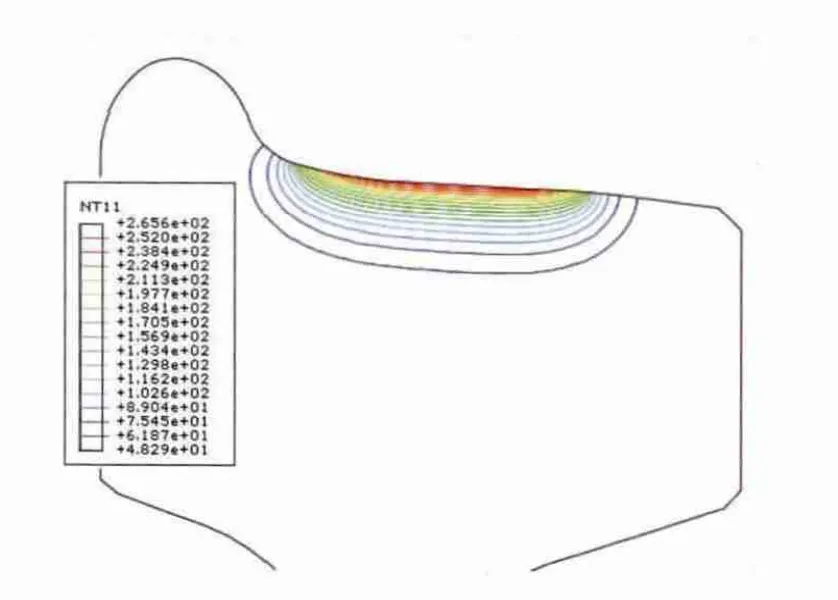
图8 踏面出现最高应力时的温度分布图
4 不同接触面积对热负荷的影响
利用热—机耦合有限元模型分析了闸瓦和车轮在不同接触面积条件下的车轮踏面制动最高温度的变化规律,该规律如图9所示。从图9可以看出接触面积从完全接触的85% ~50%的变化过程中,车轮踏面最高温度从384.5℃变化到547.5℃,最高温度出现的时间逐渐提前,从 26.4 s提前到 23.4 s,总共提前了 3 s。
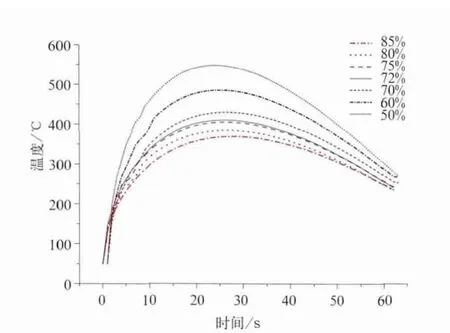
图9 不同接触面积条件下的车轮踏面制动最高温度的变化规律
分析接触面积从完全接触的50%时的踏面最高温度及应力随时间变化的曲线如图10所示。从图中看出圆周应力在紧急制动过程中,在3 s内从零很快地增加到-500 MPa,然后在47 s内逐渐减小到零,然后又在12 s内逐渐增加到370 MPa。整个紧急制动过程中接触表面出现高温度位置的圆周应力经历了500 MPa压应力到370 MPa拉应力的变化过程,这种拉压的交变过程促使了在车轮踏面制动过程中表面出现横裂纹。不同接触面积条件下的车轮踏面圆周应力的变化规律如图11所示,从该图中看出车轮与闸瓦的接触面积变化对车轮圆周应力最大压应力的数值影响不大,但对出现的时间和制动结束时车轮表面拉应力影响较大,接触面积越大,最大圆周压应力出现的时间越晚,接触面积低于全面积的70%时开始出现圆周拉应力,这种应力分布对车轮非常不利,所以在车轮踏面闸瓦制动过程中,应严格控制出现车轮和闸瓦的不匹配接触。
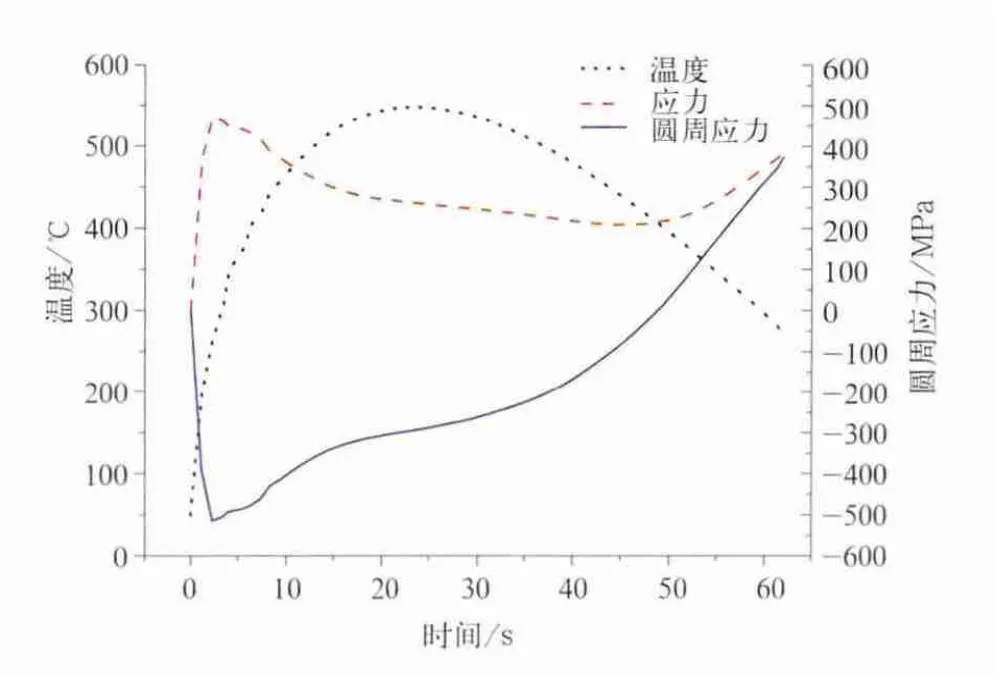
图10 踏面随时间变化的最高温度变化曲线及应力变化曲线
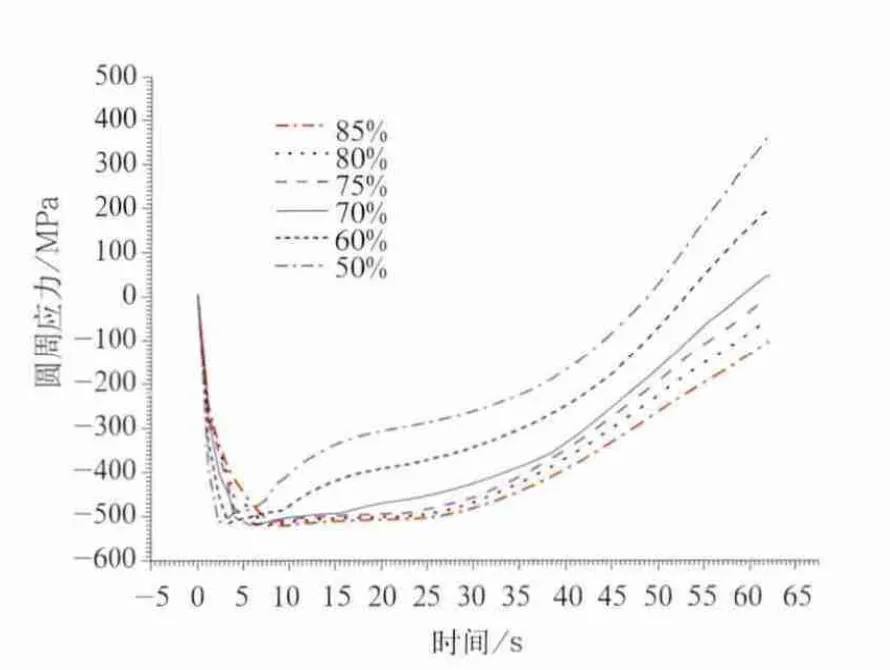
图11 不同接触面积条件下的车轮踏面圆周应力的变化规律
5 轴重对热负荷的影响
利用上述车轮踏面制动的热—机耦合模型分析了23.7,25,30,32.5 t轴重条件下的车轮热负荷。利用重载列车制动力/t不变的原则,可得到我国的大轴重重载车轮踏面制动的闸瓦压力及摩擦系数的计算表,如表2所示。
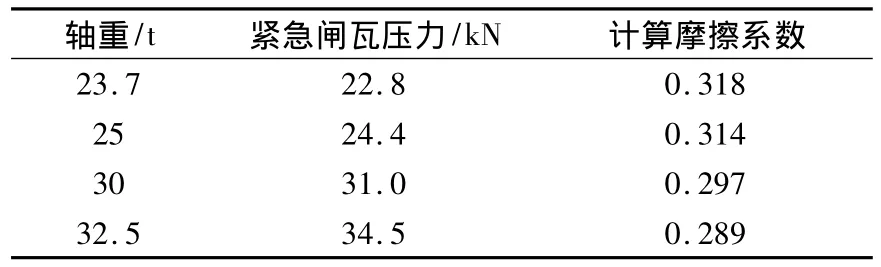
表2 重载货车紧急制动闸瓦压力及摩擦系数计算表
车轮和闸瓦的接触面积按总面积的72%来计算,紧急制动初速120 km/h。紧急制动过程中最高温度的变化如图12所示。从图12看出:轴重从25 t增加到30 t,最高温度从470℃增加到515℃,轴重从30 t增加到32.5 t,最高温度从515℃增加到561℃,说明随着轴重的增加,踏面制动的最高温度呈加速增长的趋势。
大轴重车轮踏面制动圆周应力的变化规律如图13所示。从图中看出轴重的增加对车轮圆周应力最大值的影响较小,但对车轮圆周应力达到最大压应力以后的变化过程有较大影响,轴重从25t以上,车轮圆周应力在制动的后期逐渐的变成拉应力,轴重越大拉应力越大。轴重增大以后这种圆周应力从压应力变拉应力的交变过程促进圆周的热负荷横裂纹萌生和扩展。
图14为32.5 t大轴重车轮踏面制动最高温度随速度变化规律图。随着速度的提升,大轴重车轮踏面的制动温度大幅增加,特别是从90 km/h提速到120 km/h,车轮温度从350℃以下上升到550℃以上,容易引起车轮踏面的局部高温。
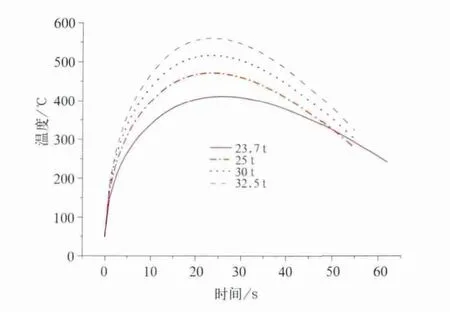
图12 大轴重车轮踏面制动最高温度的变化规律
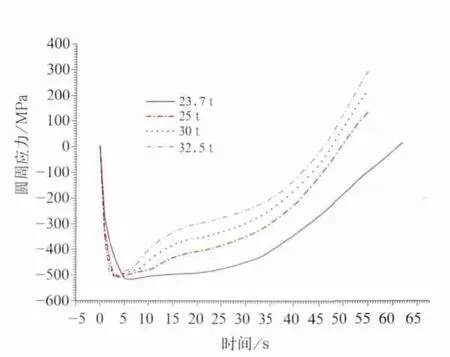
图13 大轴重车轮踏面制动圆周应力的变化规律
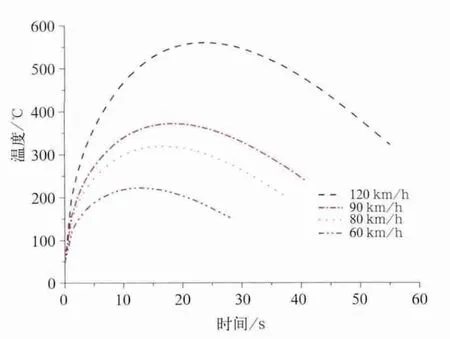
图14 32.5 t大轴重车轮踏面制动最高温度随速度变化规律
6 结论
(1)利用车轮踏面制动的热—机耦合模型进行制动试验台的数值模拟,计算结果和试验台结果吻合较好,说明该方法的有效性。
(2)当车轮与闸瓦接触面积小于闸瓦总面积的70%,在紧急制动时车轮表面容易出现圆周拉压交变应力,这会促使车轮表面出现制动横向裂纹。
(3)重载列车制动力/吨不变的原则条件下,120 km/h紧急制动时,轴重为30t的车轮表面温度达到500℃,轴重为32.5 t的车轮表面温度达到600℃左右。比较接近车轮用钢开始发生奥氏体转化的临界点730℃,这对车轮的使用寿命不利。
(4)轴重增加以后(大于25 t),在紧急制动时车轮表面容易出现圆周拉压交变应力,这会促使车轮表面出现制动横向裂纹。
(5)对于32.5 t轴重的货车初速90 km/h紧急制动时与23 t轴重的货车在120 km/h紧急制动时的热负荷水平一致。
[1] 王京波.合成闸瓦对车轮热影响的研究[J].铁道机车车辆,2003,23(2):74-79.
[2] 刘俊红.重载货车踏面制动热响应分析研究[D].成都:西南交通大学,2006.
[3] 关 莹,谢素敏,兆文忠.踏面制动热一机耦合过程的数值仿真[J].大连铁道学院学报,2003,24(3):9-12
[4] 马大炜.铁道车辆制动热负荷的计算及应用[J].中国铁道科学,2000,21(4):30-37.
[5] TED B,LIU Wingkam,BRIAN M.Nonlinear Finite Elements for Continua and Structures[M].New York:2000.
