基于SVPWM的变参数MRAS速度辨识模型仿真与研究

夏浩瑄，刘子胥

（河北工业大学电气工程学院，天津 300130）

基于SVPWM的变参数MRAS速度辨识模型仿真与研究

夏浩瑄，刘子胥

（河北工业大学电气工程学院，天津 300130）

根据矢量控制理论，分析和探讨了三电平逆变系统SVPWM控制算法分解成为两电平SVPWM控制算法的方法，并且阐述了如何有效地控制中位点电压平衡问题。建立基于变参数MRAS速度辨识理论的无速度传感器矢量控制系统在三电平逆变电路控制下电机Simulink仿真模型。得到了电机良好的动态特性曲线，验证了三电平SVPWM调制策略对电机控制的稳定性及可靠性。将MRAS模型得到的推算速度与测量速度对比，仿真结果表明用变参数MRAS速度辨识数学模型推算电机转速是可行的。

三电平；空间矢量脉宽调制；模型参考自适应；无速度传感器

1 引言

空间矢量脉宽调制（SVPWM）作为一种受广泛关注的逆变器调制技术，具有开关损耗小，电压利用率高，计算简单，易于实现数字化等优点，因而在电气控制各个领域中得到大量的应用。

在矢量控制系统中，无速度传感器交流调速系统既减少了设备的使用量，增加了系统的可靠性，又避免了采用速度传感器检测时可能带来的误差。其理论基础是基于测量电机定子电压和电流等参数，结合电机数学模型和物理量间关系，推算出电机转速，用于速度反馈［1］。本文采用的变参数MRAS速度辨识理论是将传统的矢量控制系统增加一个由参考模型和控制器参数构成的自动调节回路。

2 三电平逆变器SVPWM优化计算

SVPWM是三电平逆变器和电动机的有机结合，其电压由8个基本电压矢量叠加而成。从而得到逆变器开关管的相应状态，结合电机磁链和电压的关系，实现电机的变压变频调速。

2.1 三电平SVPWM转化到两电平的计算

三电平逆变电路比其他多重逆变电路简单，且它的输出容量大，输出电压谐波含量小。中点钳位型三电平逆变电路是典型的电压型逆变电路，每个主开关器件关断时所承受的电压相对较小，是直流侧电压的一半。

所谓三电平逆变器是指每相的输出电压有3种取值U0=+Vdc/2，U0=-Vdc/2，U0=0。分别将1/2Vdc，-1/2Vdc和0这3种电平称为“1，-1和0”状态，若引入开关函数Sa，Sb，Sc（分别可以是3种状态中的任一种），逆变器输出电压V的PARK矢量可以记作：

由于3种状态的组合是任意的，三相逆变器的输出V有33=27种状态，根据三电平空间矢量图的特性，可以把它看成由6个两电平的小六边形组成，如图1所示，图1中阴影部分是2个两电平六边形相互重叠的部分。选定小六边形，使电压参考矢量落在它的内部，落在阴影部分时，开关函数有2种选择［2-3］。把三电平空间矢量转化为两电平后，要对参考电压进行修正，然后用两电平算法选择开关状态，计算基本矢量的作用时间。

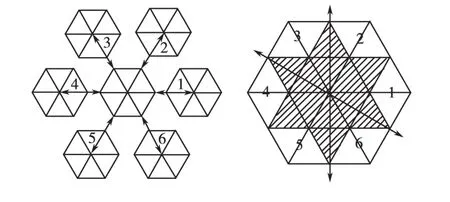
图1 三电平转化到两电平空间矢量Fig.1 Three-level transformed into two-level space vector

三相电压转化为静止坐标系的两相Vα，Vβ为

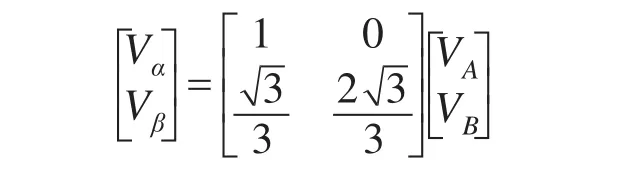
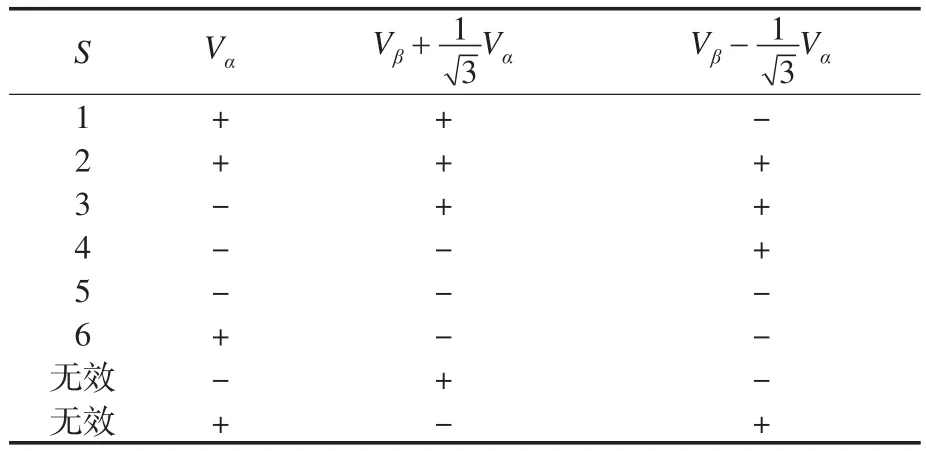
表1 S与Vα和Vβ的关系Tab.1 The relationship ofVαandVβwithS

S确定以后，要对参考电压进行修正，平移参考电压，使它的起点为S所确定的六边形的中心。通过变换得到修正参考电压。为了便于用软件实现对参考电压所在区域的判断和矢量作用时间的计算，需要将修正后的三相参考电压转化为两相电压矢量。如图2所示，Vref表示三电平系统中的参考矢量，Vr代表转化到两电平系统的矢量，所示参考电压落在了S=1，N=1的区域，可以利用两电平的方法计算矢量作用时间。Vr可以由小六边形的矢量 V6′，V4′合成。

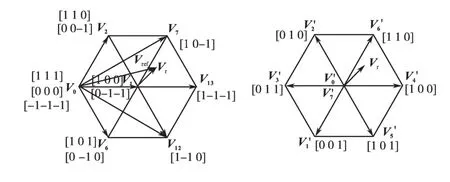
图2 参考电压的计算Fig.2 The calculation of reference voltage

2.2 中点电位平衡的控制

中点偏移会使某相电压升高或某相电压过低，这些都是设备工作时尽量避免出现的。假设使中点电位上升的矢量为正矢量，使中点电位下降的矢量为负矢量。对两电平平面分析可知，当开关函数S为1，3或5时，负矢量的作用效果优于正矢量的作用，造成中点电位下降；当开关函数S在其它区域时，中点电位上升。因此，当参考电压空间矢量位于两电平平面重叠区域时，只需要改变S的值就可以有效地控制中点电位的平衡。同时在一个PWM周期内可以少选取2个矢量，消除宽度较窄的脉冲［4-5］。

对于每个采样周期，可以通过改变作用时间来调节中位点的平衡。中点电压上升时，在一个采样周期内，增加负矢量的作用时间。反之，减小负矢量的作用时间。

3 基于MRAS速度估计模型的建立

模型参考自适应（MRAS）是在常规的反馈控制系统的基础上再附加一个参考模型和控制器参数的自动调节回路［6］。参考模型应该能代表受控系统的准确模型，其输出应该是自适应控制的期望值；可调模型就是受控系统，可以调整其参数或输入以获得尽量接近参考模型的性能。

模型参考自适应拓扑图如图3所示，x为系统输入，xo为期望输出，xo1为实际输出，e=xo-xo1为误差信号，通常e≠0，它可驱动自适应机构，调节可控模型从而减小误差，直到e在误差允许范围内。

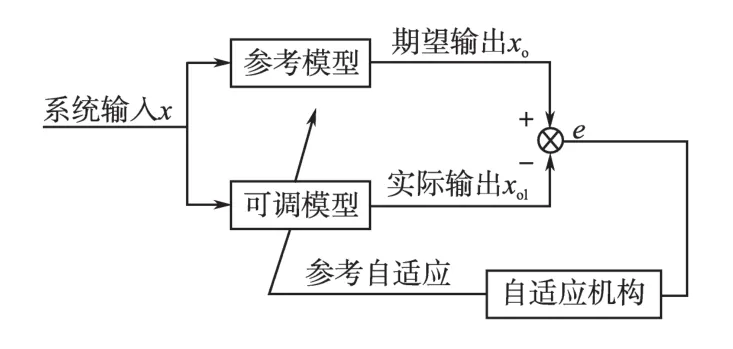
图3 模型参考自适应拓扑图Fig.3 The topology of model reference adaptive

参考模型的输出代表系统希望的动态响应，被控对象由于外界环境或工作状态改变使其运行特性偏离了最优轨线，被控对象的输出与理想模型的输出相比较，产生误差，误差驱动自适应机构，形成反馈，修正调节器的参数，促使可调模型的输出与参考模型的输出一致，即误差趋于零，从而保证系统具有良好的性能。

采用转子磁通估计法的MRAS，将不含电动机转速的电压模型作为参考模型，含有电动机转速的模型作为可调模型，利用输出量的误差构成合适的自适应率以调节可调模型参数，来达到控制对象的输出跟踪参考模型的目的。

三相异步电动机在两相静止α-β坐标系的电压模型为

由上述模型知，电压模型中不含角速度ω项，而电流模型有ω项。故用电压模型的转子磁链作为期望值，电流模型转子磁链作为推算值，以PI控制器的输出作为角速度的估算信号r，反馈给电流模型实现闭环控制［7］。转速推算结构图及模型参考自适应无速度传感控制系统结构分别如图4和图5所示。

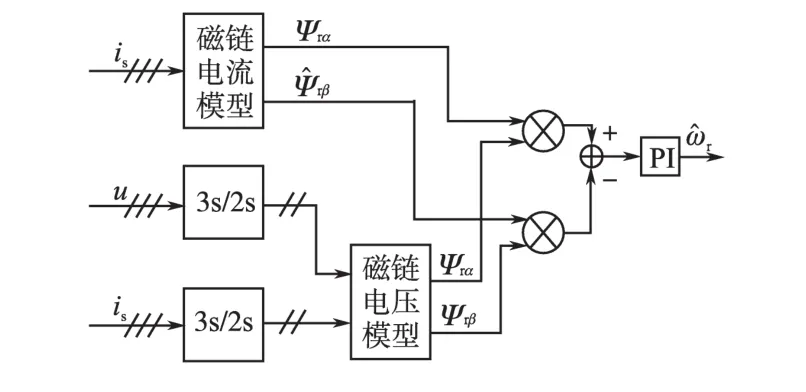
图4 转速推算结构图Fig.4 Speed calculating structure figure

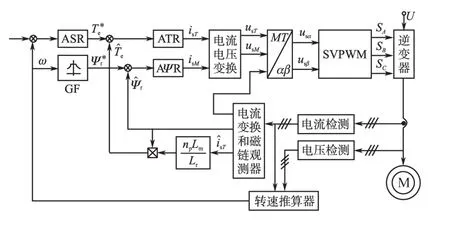
图5 模型参考自适应无速度传感器控制系统结构Fig.5 The control system of model reference adaptive with speed-sensorless

自适应机构的设计需要考虑辨识系统的全局渐进稳定性，以保证状态收敛。由于电动机的机电时间常数比电气时间常数大很多，因此可以将电机常数的角速度ωr视为常数，则电流模型变为一个线性状态方程：

根据Popov超稳定性理论求解广义误差［8］，可以得到自适应速度辨别公式：

式中：Ki，Kp为调节系数。

实际上，电压模型的纯积分环节，会引起直流漂移和初值问题，造成角速度信号r在低速时出现失真现象，需要一个高通滤波器s/(s+τ)，降低影响。

模型参考自适应在低速时，速度估计不够精确，如果Ki，Kp的取值稍大一点儿，可以使收敛速度加快，还可减少速度的估计偏差。但是较大的Ki会使转速的推算产生较大误差。因此转速升高时速度误差较小，这时Ki，Kp取较小的值以便消除静差，减少超调和稳定时间［6］。

4 基于Matlab/Simulink仿真

采用Matlab/Simulink进行仿真，模拟异步电机的启动，利用电力系统工具箱的PSB，构造仿真系统。仿真参数如下所示。

所模拟的电机参数为：额定电压380 V，频率50 Hz，2对极，Rs＝0.435 Ω，Rr=＝0.435 Ω，Ls=0.071mH，Lr=0.002mH，转动惯量J＝0.089kg·m2，机械负载转矩T=50 N·m。

以电压模型转子磁链作为期望值，电流模型转子磁链作为推算值，建立模型参考自适应电动机控制仿真模型，如图6所示。

其仿真结果如图7所示。

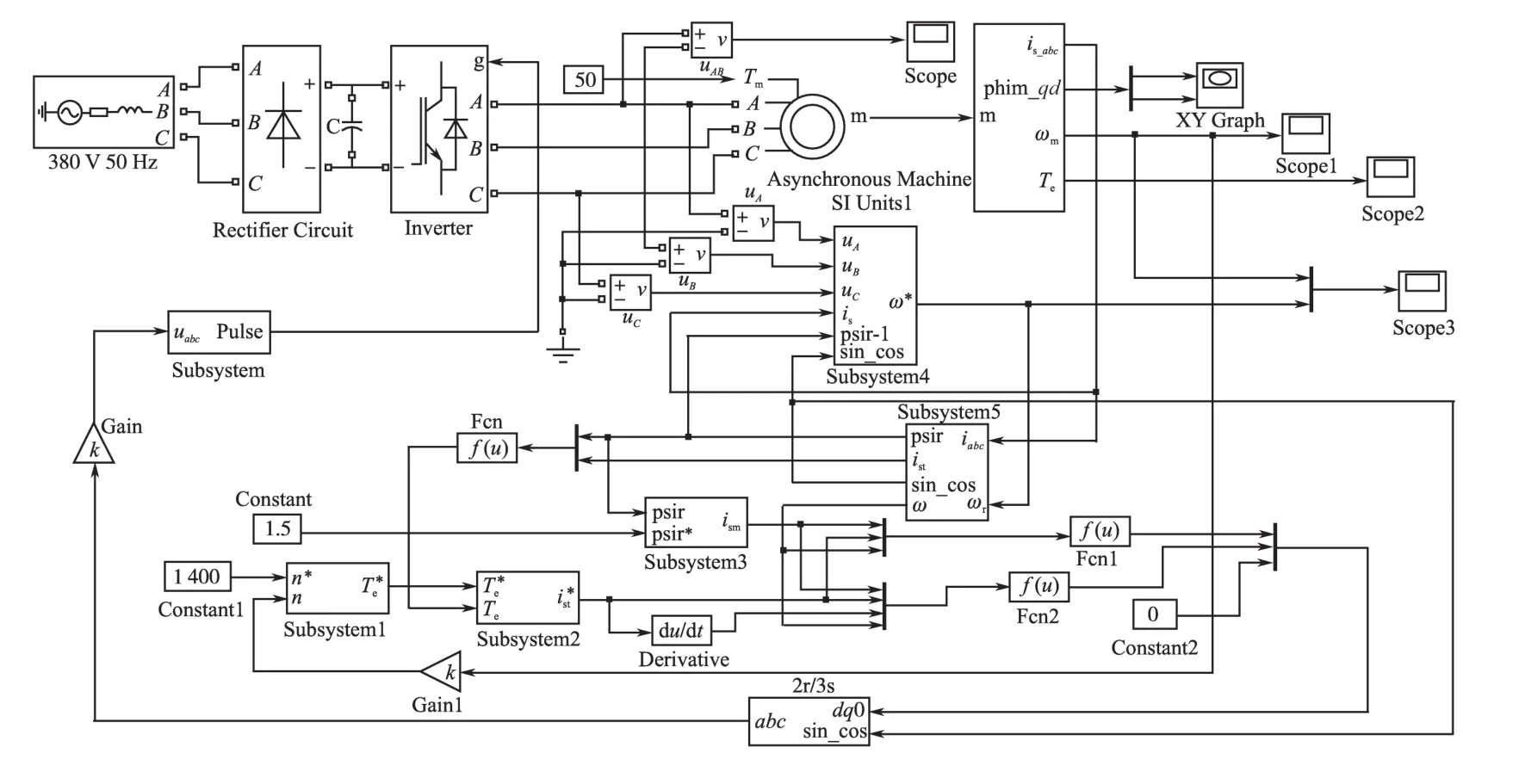
图6 模型参考自适应的电动机控制的仿真模型Fig.6 Simulation model of motor control based on model reference adaptive system

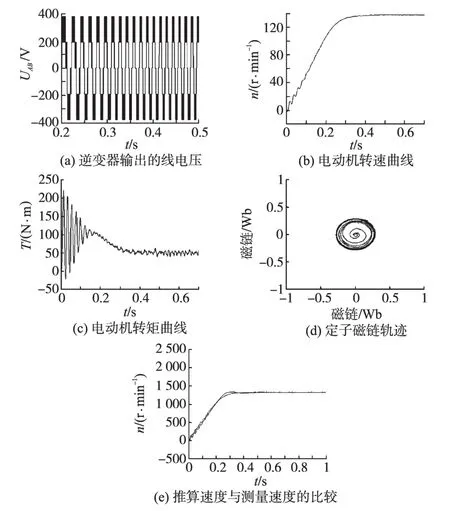
图7 仿真结果Fig.7 The simulation results

仿真结果表明：1）三电平逆变器的输出电压谐波较小，波形接近正弦波，电动机响应速度较快且运行平稳，说明三电平SVPWM系统对电机控制的稳定性及可靠性；2）在无速度传感器系统中，低速时可以有一定的误差，但在高速时电机的运行还是趋于一致，稳定运行时速度响应快，几乎没有超调。仿真系统具有良好的稳态性能和动态性能。

5 结论

在矢量控制系统中，无速度传感器交流调速系统既减少了设备的使用量，增加了系统的可靠性，又避免了采用速度传感器检测时可能带来的误差。本文将异步电动机矢量控制与MRAS速度辨识模型相结合，开展了研究。

模型参考自适应（MRAS）用电压模型转子磁链作为期望值，电流模型转子磁链作为推算值，以PI控制器的输出作为角速度的估算信号r，反馈给电流模型实现闭环控制，建立模型参考自适应的电动机控制仿真模型。通过仿真结果看出，电机运行可靠稳定，速度估算的误差较小，验证用变参数MRAS速度辨识数学模型推算电机的转速是可行的。

［1］ 王志民，冯晓云.无速度传感器异步电动机矢量控制系统的改进研究与仿真［J］.电气传动自动化，2006，28（4）：14-18.

［2］ 肖庆恩，何礼高.三电平逆变器SVPWM控制的一种简化算法及实现［J］.电气传动自动化，2004，26（5）：21-25.

［3］ Yao Zhezhi，Yi Lingzhi，Peng Hanmei，et al.Study of Simpli-fied SVPWM Algorithm Based on Three-level Inverter［C］//The Sixth International Power Electronics and Motion Control Conference-ECCE Asia，2009：304-309.

［4］ 赵刚，王磊.三电平逆变器空间矢量控制算法研究［J］.电气传动，2012，42（11）：26-29.

［5］ 朱希荣，周晓锋，周渊深.NPC三电平逆变器SVPWM算法的研究及仿真实现［J］.淮海工学院学报：自然科学版，2007，16（1）：27-30.

［6］ 王丹，姚绪梁，王晓三，等.基于MRAS变参数无速度传感器矢量控制系统的研究［J］.应用科技，2006，33（8）：22-24.

［7］ 罗慧，王军林，尹泉.PMSM自适应观测器算法低速稳定性研究［J］.电气传动，2013，43（8）：3-7.

［8］ 赵明杰，杨莹春，诸静.基于Popov超稳定性理论的模糊自适应控制器设计方法［J］.自动化学报，2001，27（3）：406-410.

修改稿日期：2013-11-19

Research and Simulation of Varying Parameters MRAS Speed Identification Model Based on SVPWM

XIA Hao-xuan，LIU Zi-xu
（School of Electrical Engineering，Hebei University of Technology，Tianjin300130 ，China）

According to vector control theory，it was explored and analyzed the method that how three-level inverter system SVPWM control algorithm converts into two-level SVPWM control algorithm，and how to effectively control the balance of median point voltage.And motor′s simulation model was created based on variable parameters MRAS speed identification theory of the speed-sensorless vector control system under the control of three-level inverter circuit.The dynamic characteristic curves validate the stability and reliability of the motor based on the control of three-level SVPWM modulation strategy.The calculation results of MRAS model are compared with the measurement speed，it testifies that using the variable parameters MRAS speed identification model to calculate the motor speed is feasible.

three-level；space vector pulse width modulation；model reference adaptive system；speed-sensorless

TM343

A

夏浩瑄（1988-），男，硕士研究生，Email：xiahaoxuantougao7@163.com

2013-08-21