变负载下的特征提取与基于CHMM算法的齿轮故障诊断

徐振黔

(中国直升机设计研究所，江西 景德镇 333000)

0 引言

传统的齿轮故障诊断研究都是针对负载不变的情况，利用齿轮振动信号的异常来单一映射齿轮不同的状态和故障，文献［1－3］就把不同的非参数方法用在恒定载荷的故障诊断上。在齿轮振动信号参数化建模应用中，Wang等［4］通过对健康状态时采用域同步平均处理后信号用AR模型建模，用线性预测误差过滤器来完成故障的诊断。Zhan等［5］引入了自适应Kalman滤波器的AR模型，来拟合振动残余信号，对不同负载下的信号采用不同阶数，通过统计学方法对AR余量信号估计来诊断。上述文献是在恒定载荷下，或是在变负载下的某个负载上单独建模，也相当于恒定负载，没有从整体上考虑负载的影响。

本研究中提出了将连续变化的载荷信号作为ARX模型的输入，以齿轮副为研究对象，对正弦性变载荷工况的振动信号进行处理，用ARX和一阶多项式模型拟合信号，以CHMM为分类器，对齿轮全生命周期进行故障诊断。

1 实验设计

试验在单级齿轮变速箱试验台上进行。动力源是一台同步转速为1750 r/min、额定动率为4.5 kW的电动机。负载由规格相同的电机改装而成，并通过控制其电流来采集不同工况下的实验数据。同时，为了对齿轮作全生命周期分析，实验过程将使齿轮超负荷运行，从而加速齿轮失效，缩短寿命。采样频率为20 kHz，每隔30 min采样一次，采样宽度10 s，因此每个数据文件含20万个采样点。速度由数字矢量驱动单元控制，负载是通过类似单元控制发电机电流。实验台集成加速度式振动传感器、编码器器、扭矩传感器及速度传感器等。

对齿轮副进行全生命周期破损试验，主动轮齿数为21，从动轮齿数为70。在额定扭矩状况下系统运行约100 h，再通过改变负载发电机电流，使扭矩作近似于正弦性的交替变化，并设定最小扭矩、最大扭矩分别为额定扭矩的0.5倍和3倍。图1是在此种状况下齿轮箱中从动齿轮的失效图，图中有5个齿完全断裂、2个齿部分裂，这个过程获得数据文件323个。为了方便数据处理，将这些数据按顺序编号，经验证去掉部分无效数据，共有315个数据供分析，分别对应1到315号。

图1 失效齿轮Fig.1 Failure gear

2 小波去噪和包络信号

传感器安装在齿轮箱的外表面，选择齿轮径向的加速传感器采集的信号作为研究对象。采集到的信号包含了较多其他非目标信号，如轴与轴承的转动信号、背景噪声等。为了提取有效的分析信号，对原始信号作小波去噪处理［6］。根据实验数据计算得到齿轮啮合频率为612.5 Hz，大齿轮转1圈的采样点数为2286，以此作为整圈振动信号用在后面的分析中。根据实验后数据分析和实验停机检测的观察，在文件259号处发现了故障，以此作为分界点前后各选取3个文件作为分析对象:载荷为50%的238号和266号，100%的236号和264号，300%的232号和259号。对以上数据作小波去噪处理，经多次尝试，选择10 dB的5层分解，并提取出包含轴不平衡信号和载荷信息的包络信号，然后做低通滤波处理(图2)。从图2中包络线可以看出，在齿轮故障前就出现了轴不平，这使齿轮受力不均，个别齿会加速损坏。在负载增加到300%时，大部分齿振动幅值增大。但个别齿反而出现了减小情况，使受力更加不均，对齿轮更加不利。

3 变负载下的ARX模型

3.1 ARX模型的建立

在变负载工况下建立其ARX模型，计算出的余量信号对齿轮的早期故障更敏感，因为采集信号的主要能量集中在啮合频率和各次谐波上，而通过ARX建模很好的提取出主要能量和载荷，轴不平衡等信号。当齿轮出现了故障会出现调制现象，啮合频率被轴转频及其倍频调制，在频谱上表现为啮合频率及其倍频上出现调制边频带。此时齿轮的理论信号可表示为:

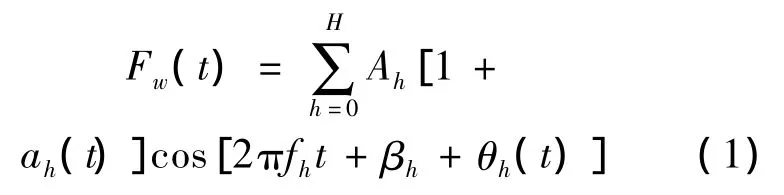
式中:h=0，1，…，H，为啮合谐波个数;A为谐波幅值;a(k)为幅值调制函数;β为初始相位;θ(k)为相位调制函数。

AR模型可以很好的拟合转速和载荷不变情况下的啮合信号，文献［7］成功地应用了AR模型来诊断齿轮轴破损。AR模型可用如式(2)表示。

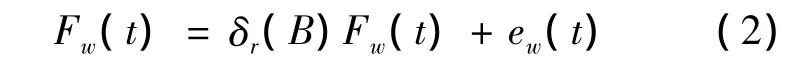
式中:δr(B)=δ1B－…－δrBr，B 为滞后算子，e为余量。

用包络信号表示变负载和轴不平衡信息，作为ARX的外部输入x(t)有:

式中，ωp(B)=ω0+ω1B+… +ωpBp，σ 为余量。将式(2)代入式(3)可以推导出:

式中，φλ(B)Bb= ωp(B)［1－ δr(B)］，E(t)= σ(t)+［1－δr(B)］ew(t)，E(t)是误差项。在下面的研究中，E(t)是主要分析对象。

图2 整圈振动信号(蓝色)和包络信号(红色)Fig.2 Vibration signal(blue)and envelope signal(red)

3.2 ARX模型阶数与参数估计

将公式(4)写成ARX模型的一般形式为:y(k)=δr(B)y(k)+ φλ(B)Bbx(k)+E(t)，y 为大齿轮的整圈振动信号，x为其包络信号，E(t)为高斯白噪声。采用最小二乘法估计模型阶数r，λ和b及其各项系数。用AIC准则来确定阶数［8］。式中，σ2N为最大似然估计，d=r+λ+b，C为常数，m为估计序列的长度。

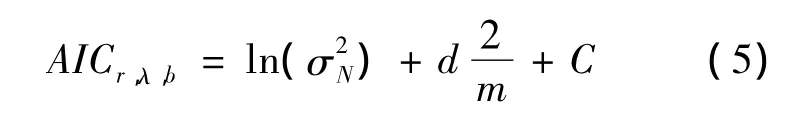
当模型的阶数和参数都计算出来时，ARX的误差项可以用式(6)计算。

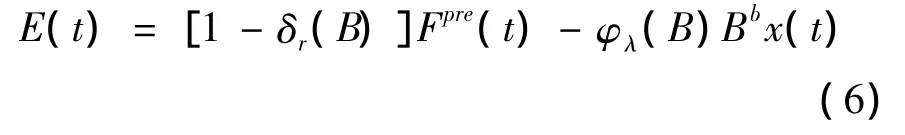
4 实验分析与CHMM特征量的提取

4.1 ARX模型的余量信号

考虑到连续变化的负载，用189～241号数据来估计ARX模型，这期间的负载呈正弦性波动，且齿轮处于健康状态，提取的整圈振动信号作为ARX模型的输出y，其包络信号用作输入x，如图3所示。从图3a中可看出，整圈振动信号的幅值反应了负载变化，图3b中包络信号单独提取了负载和轴的不平衡信息。

根据AIC准则求得各项阶次为r=66，λ=5，b=1，利用最小二乘估计系数。ARX模型估计好后利用第2节介绍的数据进行余量分析，根据公式(6)，得到ARX余量信号，如图4。从余量信号根本看不出任何信息。下面主要是对此余量信号作分析，从中提取出特征矢量，供CHMM训练与识别。

4.2 一阶多项式的残差信号

ARX模型的余量信号包含着负载信息，将用于一阶多项式的拟合以消除负载的信息，从而得到故障特征信息，最后一阶多项式的残差信号将用作CHMM的特征量，来训练和检验CHMM。

实验台通过控制电流来达到控制齿轮负载的变化。图5是一阶多项式拟合过程。从图5a和图5b可以看出，电流变化与负载变化一致，成正相关。将图4中的ARX模型余量信号分成10个区，相当于将齿轮分成10个区，每个区36°且包含7个轮齿，对每个区求标准差(Standard Deviation，SD)如图5a所示。从图5a和图5b中看到，变化趋势一致，幅值大小略有不同。用图5b电流值拟合图5a中的标准差，在用原始的标准差值与拟合的标准差值做差处理，得到了消去负载信息的残差信号(图5d)。一阶多项式模型为=B+aC为标准差估计值，C为电流值，B和a为系数。余量r=S－，S为真实值。拟合一阶多项式模型，系数如表1所示，拟合的标准差预测值(Standard Deviation Predicted Value，SDPV)如图5c所示。

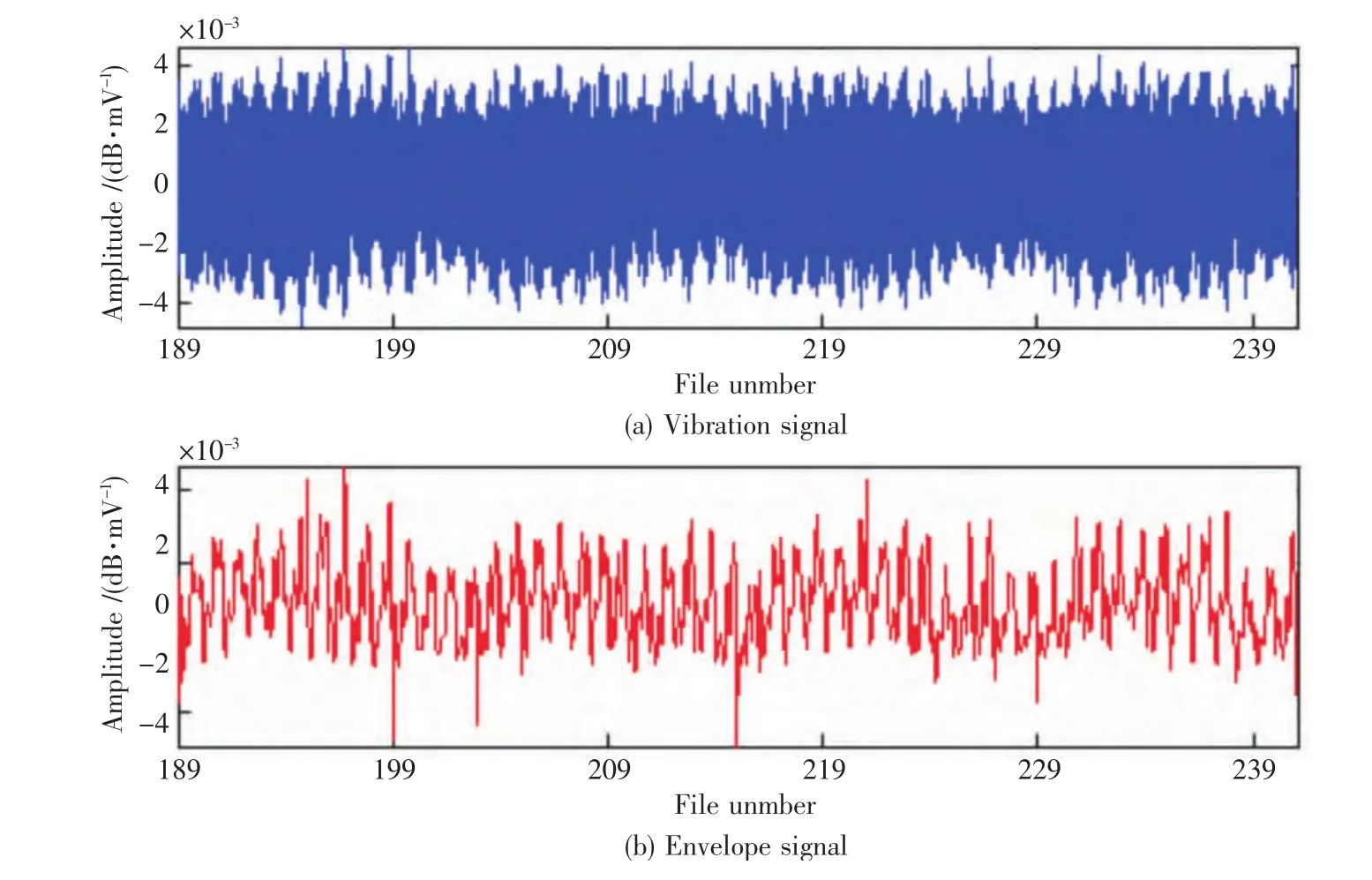
图3 189～241号数据的整圈振动信号和包络信号Fig.3 Vibration signal and envelope signal of a circle in file number 189 ～241

图4 ARX模型的余量信号Fig.4 Residual signal of ARX model

表1 一阶多项式系数Table 1 Coefficients of first－order polynomial

5 连续隐马尔科夫模型(CHMM)

把一阶多项式的残差信号作为CHMM的特征量，即观察值，通过一组概率映射到齿轮实际的隐藏的状态的过程称为HMM过程。连续HMM不需要对特征量做量化处理，较离散HMM失真小。HMM［9］的5 个主要参数为 λ =N，M，π，A，B，λ ={N，M，π，A，B}，选择左右型的混合高斯模型的连续HMM，状态数N=3，由2个高斯概率密度函数拟合单个状态的观察概率，也就是B。初始化=［1，0，0］，状态转移概率 A 均匀选取。引用Kmeans聚类算法估计出初始观测值概率模型参数B，改进多个观察值训练Buam_Welch算法来估计最优模型，并通过Viterbi算法计算测试特征序列在每个CHMM下的输出概率来决定特征序列所属的模型［10］。

图5 一阶多项式模型拟合过程Fig.5 Fitting process of first－order polynomial

利用CHMM作为分类器，对全寿命数据识别，将数据分成两部分，状态1(健康状态)和状态2(故障状态)，文中提到的259号文件分界点，以一阶多项式的残差信号作为特征序列，采集的数据文件是连续编号，将奇数号的文件用来训练CHMM，偶数号文件用作测试 CHMM。训练CHMM时，设置收敛误差为0.0001，最大迭代步数为50。训练结果如图6所示，图中纵坐标为对数似然概率(Logarithmic likelihood probability value，LLPV)表示输入特征与所输入模型的相似程度。训练结果最多12步收敛，收敛迅速，得到2个模型λ1和λ2，分别为健康状态λ1和故障状态λ2。

得到2个模型后，用偶数号文件提取的特征序列输入到2个模型中并求其对数似然概率值，见表2。从健康状态和故障状态中各随机选取10个特征序列样本输入到健康状态模型λ1中，计算对数似然概率值，健康状态特征序列所对应的对数似然概率值明显大于故障状态的概率值。反之，将测试特征序列输入到故障状态模型 中(表3)，故障特征序列所对应的对数似然概率值都大于健康状态的，表明对正常和故障两种状态成功做了识别。特别说明，经Viterbi计算的特征序列样本的概率值都很小，所以用对数表示，其绝对大小没有意义，需要的是比较其相对大小。

图6 CHMM训练结果Fig.6 Training results of CHMM

表2 CHMM健康状态测试结果Table 2 Tested result of CHMM health state

表3 CHMM故障状态测试结果Table 3 Tested result of CHMM fault state

6 结论

1)将ARX模型的特征提取方法与CHMM相结合，建立连续负载下的ARX模型应用在齿轮箱故障诊断中;

2)实例分析表明，应用CHMM分类器作用有效地诊断出齿轮故障。

［1］Kar C，Mohanty A R.Vibration and current transient monitoring for gearbox fault detection using multiresolution Fourier transform［J］.Journal of Sound and Vibration，2008，311(1－ 2):109－132.

［2］张超，陈建军，郭迅.基于EMD能量熵和支持向量机的齿轮故障诊断方法［J］.振动与冲击，2010，29(10):216－220.

［3］何田，林意洲，郜普刚，等.局部均值分解在齿轮故障诊断中的应用研究［J］.振动与冲击，2011，30(6):196－201.

［4］Wang W Y，Wong A K.Autoregressive model－based gear fault diagnosis［J］.Journal of Vibration and Acoustics，2002，124(2):172－179.

［5］Zhan Y，Makis V.A robust diagnostic model for gearboxes subject to vibration monitoring［J］.Journal of Sound and Vibration，2006，290(3－5):928－955.

［6］葛哲学，沙威.小波分析理论与MATLABR2007实现［M］.北京:电子工业出版社，2007:128－140.

［7］王细洋，孔志高，董海，等.基于自回归模型的齿轮轴破损诊断［J］.机械工程学报，2009，45(4):265－272.

［8］Ljung L.System identification:Theory for the user(2nd edition)［M］.Upper Saddle River，NJ，Prentice－Hall PTR，1999:89－112.

［9］Rabiner L R.A tutorial on hidden Markov models and selected application in speech recognition［J］.Proceedings of the IEEE，1989，77(2):257－286.

［10］谢锦辉.隐Markov模型(HMM)及其在语音处理中的应用［M］.武汉:华中理工大学出版社，1995:25－37.