SiCp/Al 复合材料回转体薄壁工件模态分析*
2014-04-27董伟亮黄树涛许立福焦可茹
董伟亮 黄树涛 许立福 焦可茹
(沈阳理工大学机械工程学院,辽宁 沈阳110159)
SiCp/Al 复合材料具有较高的比强度、比刚度、弹性模量、耐磨性和小的热膨胀系数等优良的力学性能,在航空航天等高技术领域的应用日益广泛[1-3]。薄壁圆柱壳具有重量轻、结构紧凑、整体性能高等特性,也被广泛应用于现代航空航天工业中[4]。SiCp/Al 复合材料薄壁圆柱壳由于材料中加入了高强度的硬脆SiC陶瓷颗粒以及本身的结构特性,加工工艺性较差[5]。薄壁件在切削力的作用下很容易发生振动[6],因此研究SiCp/Al 复合材料薄壁件的动力学特性具有重要的现实意义。本文应用有限元分析软件ANSYS 对体积分数为56%的SiCp/Al 复合材料薄壁圆柱壳进行了模态分析,得到了前20 阶固有频率和振型,并分析了离心力和结构尺寸对固有频率的影响,为通过优化结构尺寸和调整工艺参数来避免切削力作用下工件的共振提供了参考和指导。
1 模态分析的理论基础
模态分析的基本思想是将描述机械、结构动态性能的矩阵方程解耦,从而使n 自由度系统的动力学特性可以用单自由度系统来表示[7]。SiCp/Al 复合材料薄壁圆柱壳的无阻尼自由振动方程的矩阵表达式为
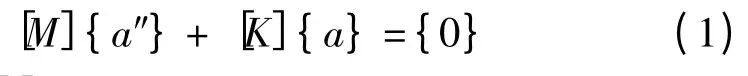
式中:[M]、[K]分别为系统的质量矩阵和刚度矩阵,均为对称阵,质量矩阵为正定矩阵,刚度矩阵为正定矩阵或半正定矩阵;{a″}为加速度向量;{a}为位移向量。设方程(1)的解为

式中:{A}为自由振动时的振幅向量;ω 为系统的频率。将式(2)及其对时间t 的2 阶导数代入方程(1)并消去eiωt后得到

根据线性代数理论,方程(3)有非零解的条件是其系数矩阵的行列式值等于零,即
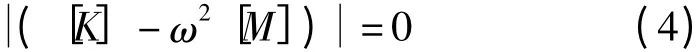
式(4)称为特征方程或频率方程。将其展开,得到一个关于ω2的n 次代数方程,它的根称为特征值。将ω2带入式(3)求出的非零解A 称之为与ω2对应的特征矢量。特征值开平方即得到ω——系统的固有频率。在质量矩阵为正定矩阵,刚度矩阵为正定矩阵或半正定矩阵的情况下,n 个特征值均为非负实数。在大多数情况下,这n 个特征值互不相等,将其按大小排列起来ω1<ω2<… <ωn。它们分别称为一阶固有频率、二阶固有频率、n、n 阶固有频率。与i 阶固有频率相对应的特征矢量记为{A(i)},它描绘了系统振动位移的一种形态,称为第i 阶固有振型或主振型,也简称为振型。
2 有限元模态分析
2.1 建模和分网
SiCp/Al 复合材料薄壁圆柱壳的几何尺寸分别为:直径D =200 mm,长L =300 mm,厚度t =5 mm。SiCp/Al 复合材料参数如表1 所示。

表1 SiCp/Al 复合材料参数
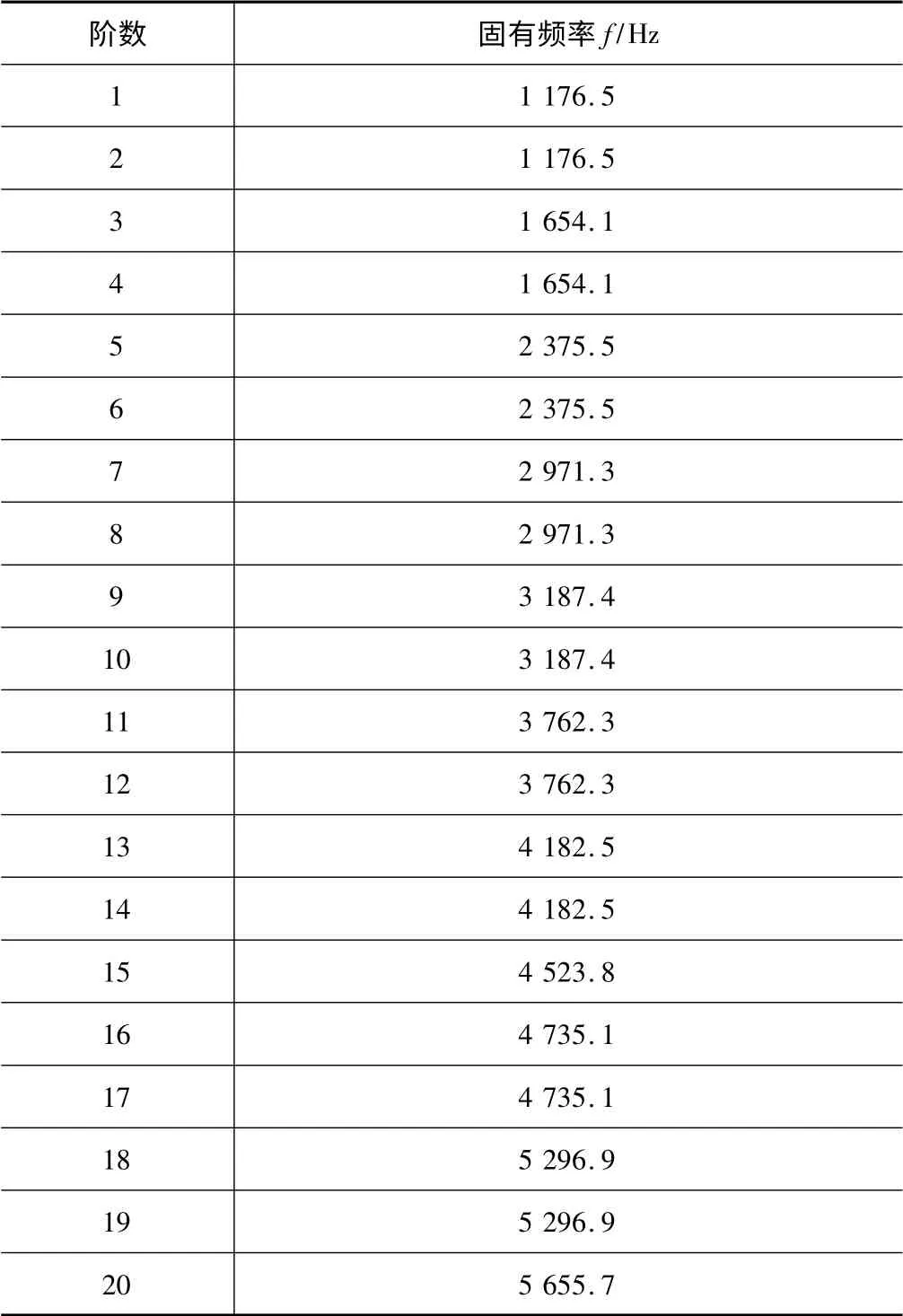
表2 薄壁圆柱壳前20 阶模态
由于圆柱壳壁厚较薄,划分网格时使用8 节点高精度壳单元shell93。设置网格大小为5 mm,采用映射网格划分方法。有限元模型最终确定有7680 个单元,23296 个节点。
2.2 加载并求解
研究进行的是模态分析,模态分析属于动态分析中的固有特性分析,固有特性由固有频率、振型等一组模态参数构成。它由结构本身(质量与刚度分布)决定,而与外部载荷无关。所以在对回转体进行模态分析时,只需施加自由度约束即可。工件加工时采用一端固定、一端自由的方式,故在模型的一端施加全约束。施加约束后的工件模型如图1 所示。

对于模态分析ANSYS 中有7 种求解模块,由于Block Lanczos 方法被认为是目前求解大型特征值问题最有效的方法,它具有求解精度高,计算速度快的特点。本文选择其中的Block Lanczos 方法求解,在求解设置中提取模态数和扩展模数均取为20,频率范围取为0~1 MHz。解得前20 阶固有频率如表2 所示。
2.3 结果分析
从前20 阶固有频率可以看出,薄壁圆柱壳各阶固有频率均较高。表中除第15 阶及第20 阶之外,相邻两阶固有频率相同,这是由于薄壁圆柱壳结构对称,会出现振型和频率相同但相位不同的情况。从各阶振型图可以看出,薄壁壳自由一端振幅均较大。第1、2、3、4、7、8、16、17 阶振型均为整体振动,且随着阶数的增加自由一端振幅较大的区域分布更为密集。第1、3、7、16 阶振型如图2 所示。
第5 阶、6 阶及15 阶振型自由一端振幅较大区域的面积较大,其中第15 阶振型表现的尤为严重。第5阶及15 阶振型如图3 所示。
第9、10、11、12、13、14、18、19 阶振型在靠近全约束一端1/3 处出现局部振型。第9、11、13、18 阶振型如图4a~d 所示。
第20 阶振型在靠近全约束一端1/3 处及靠近自由一端1/3 处均出现局部振型,如图4e 所示。在进行切削加工时应调整切削参数避免切削力的频率和以上各阶固有频率重合发生共振。
3 离心力及几何尺寸对工件固有频率的影响
3.1 离心力对工件固有频率的影响
同样的结构在不同的应力状态下会有不同的动力学特性,圆柱壳在被车削的过程中会有一定的旋转速度,所以有必要对工件进行有预应力的模态分析。在进行静力分析时对工件施加一个较高的角速度60 rad/s(即线速度360 m/min),然后进行有预应力的模态分析,结果显示有预应力的模态分析与无预应力的模态分析前20 阶固有频率相差在0.2 Hz 以内。离心力对工件固有频率的影响可以忽略。

3.2 工件厚度对固有频率和振型的影响
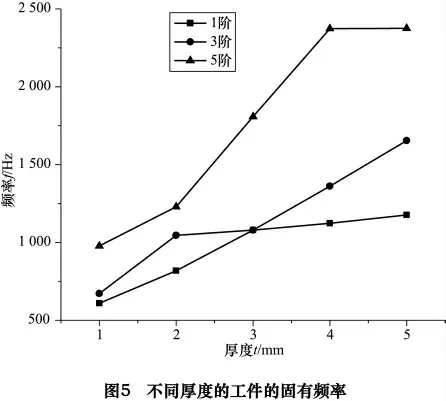
其他条件不变,分别对厚度为1、2、3、4、5 mm 的SiCp/Al 复合材料薄壁圆柱壳进行模态分析,各厚度圆柱壳的1 阶、3 阶、5 阶固有频率如图5 所示。
从图5 可以看出圆柱壳厚度由1 mm 变化到5 mm时1 阶、3 阶、5 阶固有频率总体呈上升趋势。当工件厚度由4 mm 变化到5 mm 时,1.5 阶固有频率几乎没有变化。当工件厚度由2 mm 变化到3 mm 时,工件的1 阶固有频率变化也不明显。工件1 阶、3 阶、5 阶固有频率同时发生较大变化的阶段发生在工件厚度由1 mm变化到2 mm 时。这就要求在切削圆柱壳工件的过程中,在工件厚度由5 mm 变化到1 mm 时要注意调整切削参数以防止共振。

3.3 工件长度对固有频率和振型的影响
分别对长度为100 mm、150 mm、200 mm、250 mm、300 mm,直径D 均为200 mm,厚度均为5 mm 的工件进行模态分析,不同长度工件的1 阶、3 阶、5 阶固有频率如图6 所示。
从图6 可以看出当工件长度由100 mm 变化到300 mm 时薄壁圆柱壳1 阶、3 阶、5 阶固有频率变化较大,变化趋势基本一致,频率越来越低。
3.4 工件直径对固有频率和振型的影响
当SiCp/Al 复合材料薄壁圆柱壳的直径D 分别为120 mm、140 mm、160 mm、180 mm、200 mm,厚度t 均为5 mm,长度均为300 mm 时,不同直径工件的1 阶、3阶、5 阶固有频率如图7 所示。

从图7 可以看出当工件直径由120 mm 变化到200 mm 时,薄壁圆柱壳1 阶、3 阶、5 阶固有频率变化趋势各不相同。直径由120 mm 变化到200 mm 时,工件1 阶固有频率变化不大,呈单调递减的趋势;工件直径为160 mm 时,薄壁件3 阶固有频率最高;工件直径为180 mm 时,薄壁件5 阶固有频率最低。


4 结语
(1)SiCp/Al 复合材料薄壁圆柱壳各阶固有频率均较高,而且大部分相邻两阶固有频率相同。第1、2、3、4、7、8、16、17 阶振型均为整体振动,第5 阶、6 阶及15 阶振型自由一端振幅较大区域的面积较大,其中第15 阶振型表现的尤为严重。第9、10、11、12、13、14、18、19 阶振型在靠近全约束一端1/3 处出现局部振型,第20 阶振型在靠近全约束一端1/3 处及靠近自由一端1/3 处均出现局部振型。
(2)由于车削速度较低,有预应力的模态分析结果显示,转速对工件的固有频率的影响可以忽略不计。
(3)进一步的模态分析显示不同厚度、长度、直径的薄壁圆柱壳固有频率会发生变化。
(4)所做的模态分析结果可以为切削参数的调整及尺寸的优化提供参考和指导,从而避免工件的共振。
[1]Cui yan,Wang Lifeng,Ren Jianyue.Multi-fucctional SiC/AL Compssites for aerospace appliations.[J]. Chinese Journal of Aeronautics,2008(6):578 -584.
[2]康炘蒙,程小全,郦正能,等. SiCp/Al 复合材料的拉伸性能[J]. 复合材料学报,2009,26(4):83 -88.
[3]康炘蒙,程小全,张纪奎,等.高体积分数SiCp/Al 复合材料的拉伸、压缩与弯曲特性[J].复合材料学报,2008,25(3):127 -131.
[4]韩植林.基于切削稳定性的薄壁圆柱壳切削参数优化方法的研究[D].天津:天津大学,2012.
[5]冷金凤,武高辉. SiCp/Al 基复合材料的切削加工研究现状[J]. 宇航材料工艺,2007(2):6 -9.
[6]张吉军,翟元盛,刘献礼,等. 薄壁筒件内孔车削振动建模与分析[J].机械设计与制造,2012(1):123 -125.
[7]张晓峰,周凯,赵加清.薄壁件多点柔性加工的模态分析与振动控制[J].机械科学与技术,2009(5):686 -690.
[8]张策.机械动力学[M].北京:高等教育出版社,2008.
[9]韩燕,门清毅.基于ANSYS 的球磨机回转体模态分析[J]. 金属矿山,2010(5):128 -130,147.
[10]傅中裕,杨晓京.ANSYS 的丝杠模态分析[J].机械制造与自动化,2004(6):37 -39.
[11]周鹏,胡欲立,张小军.基于ANSYS 的压气机盘模态分析[J].机械设计与制造,2005(6):61 -62.
