基于分形规则的陶瓷图案构图模型研究与应用

章义来，彭永康

(景德镇陶瓷学院，江西 景德镇 333001)

基于分形规则的陶瓷图案构图模型研究与应用

章义来，彭永康

(景德镇陶瓷学院，江西 景德镇 333001)

分形具有无穷细节的自相似性。研究提出了基于分形规则的陶瓷图案构图模型，并重点研究了迭代函数系统IFS、随机插值分形在图案拓扑结构表达中的应用，提出并深入讨论了基于分形迭代、区域迭代分割的陶瓷图案拓扑结构的初始表达及结构的迭代模式f，对构图模型及图案构图算法的实现等进行了深入研究，并最终应用本文的研究成果于陶瓷图案的构图过程。

分形；陶瓷图案；迭代；构图模型

0 引 言

20世纪70年代，法国数学家Mandelbrot 创立了分形几何学[1]。分形(Fractal)一词用来描述那些不规则而欧氏几何又无法描述的几何现象和物体[2]。分形图形是在无标度意义下具有无穷细节的自相似图形，是无序和变幻无穷的美的体现。利用分形的自相似性，可以构造出千变万化而又具有任意高分辨率结构的艺术图案。

目前，针对分形技术的研究一方面主要集中于特定领域的分形图形生成技术的研究与应用，通过分形图案生成技术的研究，发现在分形迭代过程中引入控制参数或将纹理映射技术引入分形可获得高真实自然植物模拟效果[2-5]；通过以3×3、5×5的矩阵为构图模板，基于kroneckor积的分形矩阵构图技术，实现了一种由模板决定最终图案构成的分形构图技术[6]。通过对纺织、服饰、平面木雕等行业的图案进行分析、归纳与研究，提出了基于分形几何原理且具有行业应用特征的分形图案生成算法，实现了行业应用图案的分形生成或分形重构[7，9～11]。另一方面则主要研究在分形图形的基础上，提出以分形图元为图案的构图单元，应用对称、旋转与融合等规则来进行图案构图的研究[8]。

陶瓷图案的行业应用特点决定了大量的陶瓷图案具有相似的结构，通过应用不同的图元来生成不同的陶瓷图案。分形是一种使图案的整体与局部具有自相似特征的图案构造方法，它将复杂的图案集中表示为一组规则，分形生成的图案具有高度抽象、复杂多变的特点。

本文在上述研究的基础上，提出用分形规则来描述图案的拓扑结构，将图案的拓扑结构归纳表示为一组迭代规则。由于分形具有的自相似特性，规则的构成决定了图案的总体结构。在此基础上提出一种以图元基础，分形迭代规则（IFS变换、L－系统等）为图案拓扑结构的陶瓷图案构图模型。

应用本文提出的模型生成陶瓷图案时，以初始图元为初始图案，对初始图元应用分形规则迭代得到另一图元，着色后加入图案集合，经过多次不同的分形迭代和着色过程可得到一个图元集合，该图元集合就构成了目标图案。

1 基于分形规则的陶瓷图案构图模型

基于分形规则的陶瓷图案构图模型将图案（记为P）表达为构图初元集（简称为图元集，记为U）及图案拓扑结构（亦称构图模式，记为S）构成的二元组，记为：

1.1 分形迭代图案的拓扑结构

图案拓扑结构S决定了图元在图案中的组织与呈现方式。图案的拓扑结构S由IFS系统的仿射变换集合W及迭代模式f二者构成，记为：

1.1.1 仿射变换集W

仿射变换集W的元素表述了图案分形迭代构图过程中，图元的变换处理规则，记为 。

1.1.2 图案分形迭代模式f(W，k)

图案分形迭代模式f是一个仿射变换集W、W的元素数k为参数的二元函数。迭代模式f的迭代过程见式4所示。W(k)的值可用式4所示的迭代过程计算：

1.2 区域迭代分割图案的拓扑结构

在陶瓷图案区域迭代分割生成图案的过程中，图案构图矩形区域 是图案构造的起点。图案的拓扑结构S由构图区域集D与区域分割模式f二者构成，如式5所示：

区域分割模式S=D，k的功能是将区域D分割为k个不相交的子集的集合，且分割生成的区域子集满足条件

1.2.1 构图区域D

区域Di的边界Ri是一个由直线段首尾相接形成的封闭回路。结构R可归纳为式6所述。

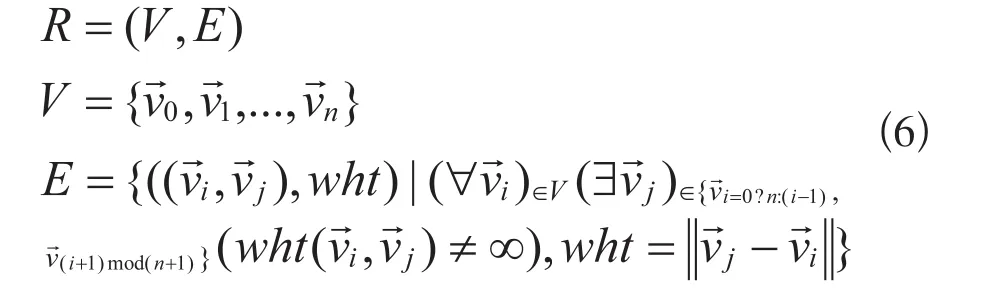
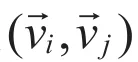
其中，区域的边的权值wht取向量的模长表示，则区域边界R的每个顶点均有两条边相连，顶点的度deg(vi)=2。

如果区域V中的端点矢量 按回路中引用该矢量的先后次序排列，则式6所示的区域边界R可用式7所述的格式来表达。

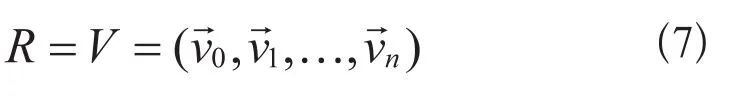
1.2.2 区域的k－SEGMENT迭代模式

区域分割就是应用模式g(D，k)将区域D划分成k（k＞1）个不相交的子集Di，i=1，...，k的过程。

式8的递归表示如下：

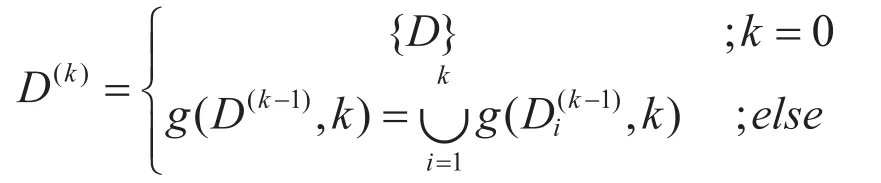
D(i)为区域第i次分割后的子区域集，是对区域第k-1次k分后的区域集D(k-1)的第1子区域集。

本文将以k=2为例分析区域分割的原理与算法。

1.3 图元构成

图元有阵列图元A（亦称像素图元）、矢量图元Fu两类。阵列图元通常以图像形式集中存储，以Am×n表示之。矢量图元Fu是根据图元的几何特性来绘制图元，由点、线、区域等构图要素按一定顺序构成。矢量图元的特点是图元缩放处理后不失真，图元占用空间较小。

矢量图元是由构图要素v组成的n元组，用式9所示。

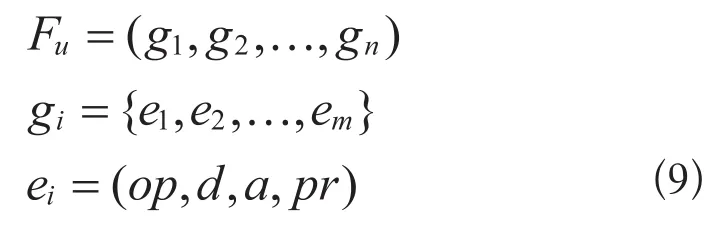
构图要素vi（简称图素）指图元构成的基本元素，通常是一个有穷元素ej的集合。ej可用式7中的四元组(op，d，a，pr)来表示，其中op－矢量类型，可以点、线（直线、曲线等），d－矢量数据，a－矢量的附加属性数据，如颜色、区域处理（透明、不透明等），pr－优先级等。

矢量图元依图元构成情况分为单一函数图元、复合矢量图元两类。

单一函数图元指用一个函数即可完整描述的图元，如直线段、圆和椭圆、各类曲线（二次曲线、正叶线、星茫线、多边形等）。复合图元指由点、线、区域等图素的综合。

2 分形图案构图模型应用

2.1 再论IFS迭代分形构图码w

在仿射变换应用的等概率假设下，IFS分形构图码W的元素w=(a，b，c，d，e，f)。

设图元中心为（0，0），则w还可用矩阵表示：

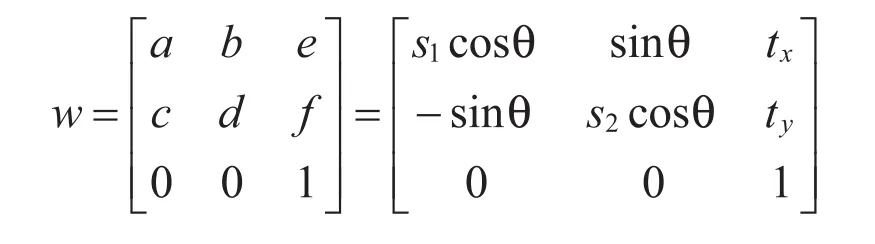
式中s1，s2为图元的缩放因子，角度θ为图元的旋转角度，角度θ为正，表示逆时针方向旋转，反之顺时针旋转。tx，ty为图元的平移距离。

生成分形图案时，码元素的分布规律，称为轨道。例如图1所示的分形图案，码元素平均分布在一个圆周上，其轨道为圆周（且圆周半径r=1）。

码元数量Lt(W)=7，亦即将圆周七等分，相邻码元的迭代计算中心与图案中心点（0，0）的圆心角夹角 =360/7=51.42°。分形码元wi(i=1，…，7)的处理中心为则有

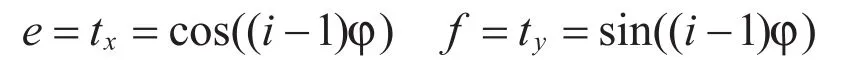
如果码元wi(i=1，…，7)的局部坐标系的x轴通过图案中心（0，0），则图元在wi(i=1，…，7)处的旋转角度 。

图1所示的分形图案的码元集W为(见表1)。

图1 分形图案Fig.1 Pattren fractal

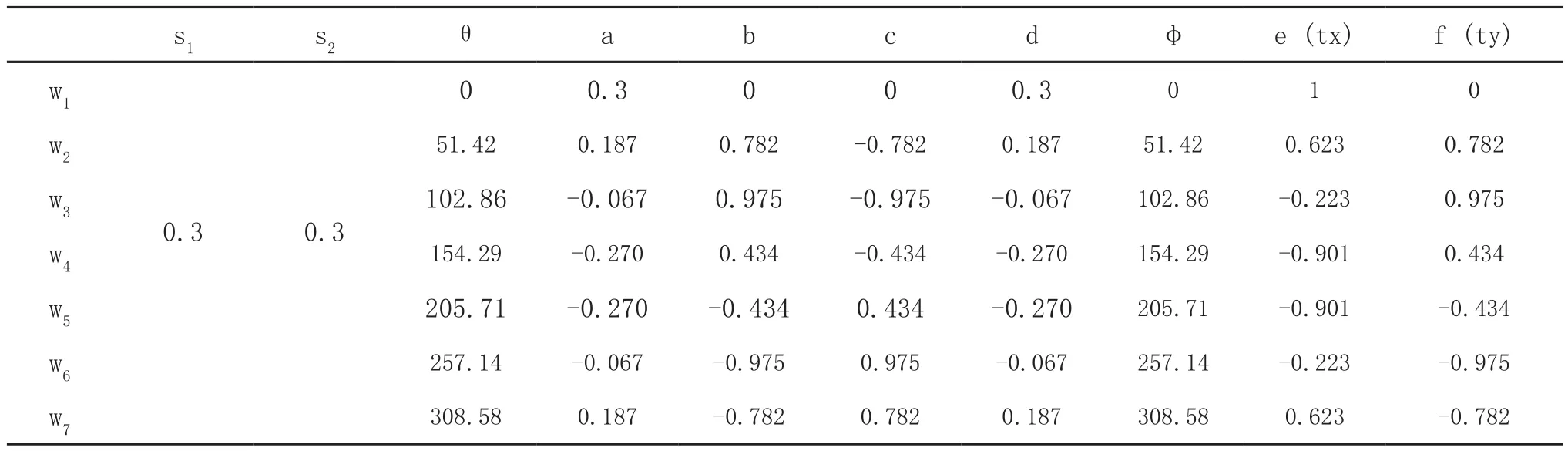
表1 分形图案码元集WTab.1 Pattern fractal element-code set

2.2 图案区域2—SEGMENT迭代分割

2.2.1 区域的2－SEGMENT模式g(D，2)过程

在区域2分分割法生成图案过程中，g(D，2)亦可写成g(R， 2)，g(R， 2)的原理是：

(1）在区域D的边界R（如式11）中，任取两边，分别为e1＝(vi，vi+1)，e2=(vj，vj+1)；

(2）在边e1，e2中各取一点，分别记为p1，p2，构造边e=(p1，p2)加入R，可将R分割为两个区域R1，R2，且

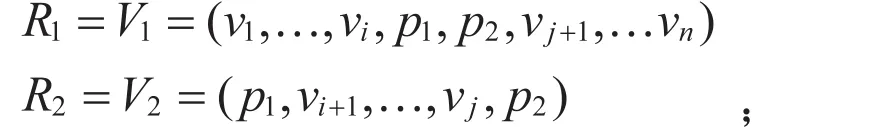
边（vi，vj）上的点p可采用来计算，其中k取值须满足条件0≤k≤1，可采用黄金分割法或随机法确定它的值。在黄金分割法下，k=0.618。在随机取值法下，k=rnd(1)为0～1间的随机数。

2.2.2 区域的2－SEGMENT迭代

基于区域2－SEGMENT模式的区域迭代分割过程，可将式8简化为式10。

式10表明，从图案的初始区域开始，每次以前一次调用R(k-1)=g(Rk-2，2)的执行结果为基础，继续调用R(k)=g(Rk-1，2)来对Rk-1中的子区域进行2－SEGMENT分割，如此不断重复迭代，直到达到规定的结果为止，即可完成区域的2－SEGMENT分割，最后再对分割产生的子区域进行构图的最终处理即可得到分形图案。

式10的递归形式表示如下（见式11）。

3 基于分形规则的图案构图算法

应用本文提及的构图模型来进行图案构图时，需指定构图的类型ptype（指分形迭代构图or 区域迭代构图）、图元U、初始图案拓扑结构S（值为W或者D）及常数k四个参数。应用模型构图的算法描述如下：

1)图案拓扑结构生成模式选择生成，通过ptype的值来选择。

如果ptype=分形迭代构图，则图案拓扑结构C＝f(S， k)；

否则为区域迭代构图模式，C＝g(S， k)；

2) for each e in C do begin

p← h(U，e)；//h(U，e)应用规则e对图元U进行处理

P←P∪{p}；

end for；

3)调用ShowPattern(P) 显示图案P，结束。

4 算法生成的图案

5 分形图案的连续性

5.1 分形迭代法生成图案的连续性

陶瓷图案分形迭代构图时，图案的拓扑结构是由图元仿射变换集W和分形迭模式f两者共同表达。其中，W侧重表述了一次迭代过程中图元的变换构图规则，分形迭代模式f描述表达了图案的迭代运算规则。W的元素具有确定性、多变性的特点。确定性是指W的元素一旦确定，即便选择不同的图元进行构图，算法生成的图案仍拥有相同的结构，如图2中a～b所示的图案，多变性是指W中的元素个数、它的每个码元的值都是可变的，上述可变因素的任何变化，均可生成不同结构的图案（如h所示的图案，具有明显的平面特征，适用于建筑陶瓷行业产品尤其是瓷砖的装饰。该方法生成的图案应用于建陶瓷砖生产中，产品的二方、四方连续要求也是需要考虑的问题。区域分割采用随机插值的原理进行分割，其生成的图案具有明显的随机性。对图案的二方、四方连续的要求，可以通缩小图案初始区域，应用对称原理将区域迭代分割产生的图案对称变换分布到整个图案空间来满足。

图2 分形图案示例Fig.2 Examples of fractal patterns

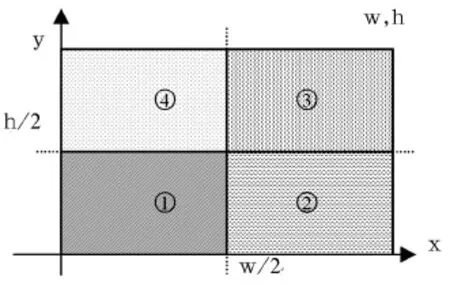
图3 构图区域Fig.3 Pattern composition domain

图案的二方连续有水平、垂直两种连续方式，以水平二方连续为例，构图的初始区域为 ，区域涵盖图3所示区域划分中的子区域①和④。

图4 具有连续特征的区域迭代分割图案Fig.4 Continuous pattern generated via iterative domain decomposition

对子区域②和③中的每个点q，可用下式建立其与子区域①和④中的点p的映射：

同理，对图案四方连续可用图案中心对称处理生成，可使初始区域为 ，区域为图3所示区域划分中的子区域①。区域②、③和④的点与区域①的点的映射关系如下：

区域②与区域1的映射：

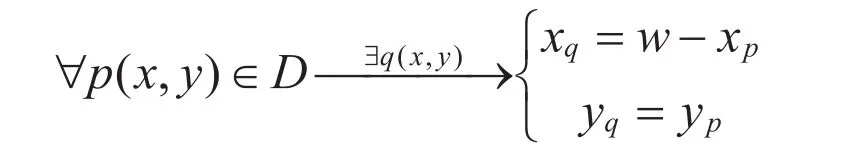
区域③与区域1的映射：

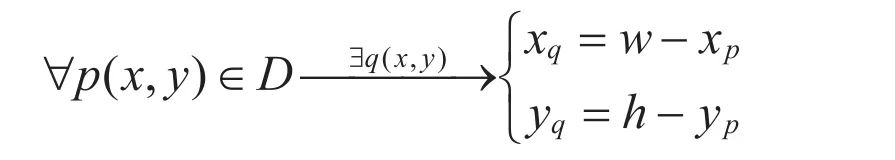
区域④与区域1的映射：

应用上述改进后的区域迭代算法，生成的符合连续要求的图案如图4所示。

6 结 论

本文提出的基于分形规则的陶瓷图案构图模型，首次将分形技术应用于图案拓扑结构的描述与表达。应用本模型进行陶瓷图案构图时，模型使用分形模型（或分形规则）来描述图案的拓扑结构，选用不同的图元可生成结构复杂多变、具有整体与局部自相似特征的陶瓷图案。本文的研究成果是对行业应用中的图案构图方法的拓展。基于本文方法生成的图案可用于日用及建筑陶瓷产品装饰，研究的理论及算法具有理论及实践意义。本文的研究成果已成功应用于陶瓷图案生成系统，文中的分形图案均由本系统生成。

[1] WHITTAKER E T， WATSON G N. A Course of Modern Analysis. Cambridge， UK： Cambridge University Press， 1952.

[2] 罗 燕， 吴中福， 郭选昌. 基于改进分形算法和位移纹理映射的仿真“竹”的实现[J]. 计算机科学， 2009，12(36)：285-289.

LUO Yan， WU Zhongfu， GUO Xuanchuang，Computer Science. 2009，12（36）：285-289.

[3] 孙天凯， 邵晓根， 王兴元. 扩展的分形L-系统与自然景观的动态模拟. 计算机工程与应用[J]， 2009，45(2)：182-185.

SUN Tiankai， et al. Computer Engineering and Applications. 2009， 45(2)： 182-185.

[4] 丁 欢， 万旺根， 余小清， 等. 基于几何参数的植物真实感模拟[J]. 计算机应用， 2009，1：97-100.

DING Huan， et al. Journal of Computer Applications. 2009， 1： 97-100.

[5] 魏宝刚， 庞向斌， 朱文浩，等.基于纹理渲染的分形图案设计[J]. 中国图象图形学报，2006，5：689-694.

WEI Baogang， et al. Journal of Image and Graphics. 2006，5：689-694.

[6] 彭永康， 章义来， 田 原. 基于模板分形的建筑陶瓷图案设计[J].计算机应用， 2010，6：1565-1567.

PENG Yongkang， ZHANG Yilai， Tianyuan， Journal of Computer Applications. 2010，6：1565-1567.

[7] 王小铭. 分形图案的构图艺术及其计算机实现[J]. 计算机辅助设计与图形学学报， 2001，1：83-86.

WANG Xiaoming， Journal of Compture-Aide Design &Computer Graphics. 2001，1：83-86.

[8] 李成杰， 刘弘， 李 霞. 基于分形图元的规则构图[J]. 计算机工程， 2009，10：213-215.

[9] 李海林， 柳炳祥， 詹棠森. 分形图案及其在陶瓷中的应用[J].中国陶瓷工业， 2006，10，30-33.

LI Hailin， LIU Bingxiang， et al. China Ceramic Industry， 2006， 10： 30-33.

[10] 丁灿剑. 基于分形的木工平面雕刻图案生成方法的研究[D]：硕士学位论文. 中南林业科技大学，2007，6.

[11] 徐向红. 分形理论在服饰图案设计中的应用基础研究[D]：硕士学位论文. 吉林大学，2009，(10).

[12] 彭永康， 章义来， 等.日用陶瓷设计构图的计算机算法[J].陶瓷学报，2004， (4).

PENG Yongkang， et al. Journal of ceramics， 2004， (4).

[13] 罗贤海， 肖绚， 张亚林， 等. 基于分形理论的陶瓷装饰软件开发[J]. 陶瓷学报，2005(2).

LUO Xianhai， et al. Journal of ceramics， 2005(2).

Research and Application of the Ceramic Pattern Composition Model Based on the Fractal Rule

ZHANG Yilai PENG Yongkang
(Jingdezhen Ceramic Institute, Jingdezhen 333001, Jiangxi, China)

A fractal is a self-similar pattern with infnite detail. This paper proposes a ceramic pattern composition model based on the fractal rule. It mainly discusses the application of iterated function system and randomized interpolation fractal to the representation of a pattern’s topology. An initial visualization of a ceramic pattern topology is realized via fractal iteration and iterative domain decomposition and the iterative mode f is obtained. The construction of the model with its pattern composition algorithms is described in detail, and is fnally applied to the practical generation of ceramic patterns.

fractal; ceramic pattern; iteration; pattern composition model

ZHANG Yilai(1965-),male,Ph.D.,Professor.

TQ174.79

A

1000-2278(2014)01-0071-07

2013-10-20。

2013-10-28。

国家科技支撑计划资助项目(编号:2012BAH25F02)；国家自然科学基金资助项目(编号:61262038)；国家科技支撑计划资助项目(编号:2013BAF02B01)

章义来(1965-),男，博士，教授。

Received date:2013-10-20. Revised date:2013-10-28.

E-mail:jdzzyl@163.com