基于IMM-MHT算法的杂波环境多机动目标跟踪
2014-04-26邵俊伟
邵俊伟,同 伟,单 奇
(1.中国电子科技集团公司第38研究所,合肥 230088;2.陆军驻中电集团38所军事代表室,合肥 230088)
0 引 言
随着战场环境的日趋复杂以及目标机动性能的日益提升,如何在杂波环境下跟踪机动目标正成为雷达数据处理系统要应对的关键问题之一。传统数据关联算法,如最近邻[1](NN)、概率数据关联[2](PDA)、联合概率数据关联[3](JPDA)等,以当前扫描周期内的量测为基础进行数据关联,若某一扫描周期内的关联结果与真实情况有较大差别,则之后的跟踪过程常会发生错误,甚至丢失目标。多假设跟踪[4](MHT)的关联结果不仅取决于当前扫描周期内的量测数据,而且还与历史量测信息有关。对不能确定的关联,会形成多种逻辑假设,并用后续的量测数据来解决这种不确定性。在理想条件下,MHT是最优的数据关联算法,可以有效地解决杂波环境下的数据关联问题。但是,MHT算法所需的计算和存储资源会随着量测数和跟踪步数的增长呈指数增加,若要实际应用,还需要有效的假设管理技术。
对机动目标,以单一的运动模型来刻画其运动过程,往往和实际情况有偏差,最终会由于模型失配导致跟踪误差增大甚至跟踪失败。交互多模型[5](IMM)算法使用多种运动模型对目标进行跟踪,模型间的转换服从已知转移概率的有限Markov过程。在跟踪过程中对各模型的概率进行更新,可以起到自适应调整模型的作用,得到较好的跟踪效果。
本文将IMM跟踪算法与MHT关联算法结合起来,并采用文献[6]在解决视频跟踪问题时所用的MHT假设生成和假设管理技术,来实现杂波环境下对多机动目标的跟踪。仿真结果验证了此方法的有效性。
1 算法描述
1.1 MHT算法原理
1979年Reid[4]针对多目标跟踪问题,基于“全邻”最优滤波器和Bar-Shalom的聚概念,提出了MHT方法。此算法的执行可以分为假设生成、假设概率计算和假设管理3个步骤。
1.1.1 假设生成
记Ωk为直到k时刻的关联假设集合,Zk={zk,1,…,zk,mk}为k时刻的量测集合;Zk为直到k时刻的累积量测集合。Ωk由直到k-1时刻的关联假设集Ωk-1和当前量测集Zk关联得到,规定每个目标至多与一个落入跟踪门内的当前量测关联。
若每条假设航迹与落入跟踪门内的所有量测都进行关联,则生成的假设航迹数量会随目标和量测数目的增加而急剧增长,无法满足实时跟踪的需求。利用Murty算法,可以在不生成所有假设的条件下,得到前M个概率最大的关联[6]。先构造1个分配矩阵,行对应量测,列对应目标、杂波或新目标,矩阵的元素是量测来自于相应目标的负对数概率,或是量测来自于杂波或新目标的负对数概率,这样前M个概率最大的关联,即是该分配矩阵前M个费用最小的分配,而后者可以通过Murty算法求解[7]。
1.1.2 假设概率计算
记θk为k时刻量测与目标的关联事件,该事件中τ个量测源于已建立航迹,v个量测源于新目标,ψ个量测源于虚警。引入如下记号:

设Θk,l表示关联假设集Ωk中的第l个假设,由假设生成的概念,它由Ωk-1中的某个假设Θk-1,s和关联事件θk组合得到,即Θk,l= {Θk-1,s,θk} 。利用Bayes公式,可以得到假设Θk,l的后验概率[8]:


在缺乏先验知识的情况下,一般可假定虚警和新目标在跟踪门内服从均匀分布,新息服从Gauss分布,而虚警和新目标的数目服从Poisson分布。
1.1.3 假设管理
随着跟踪步数的增加,关联假设的个数会呈指数增长。为提高MHT算法的执行效率,可以使用如图1所示的假设树来进行关联假设的管理[6]。

图1 MHT假设树
该假设树通过以下2个参数对关联假设进行管理:
(1)非叶子结点的子结点数M:表示前一时刻的假设集Ωk-1中的每个关联假设Θk-1,s,在与当前时刻的量测集Zk进行关联时,仅保留前M个概率最大的关联假设。
(2)树的深度N:表示只记录最新N个扫描周期内的关联假设信息。
每步生成新的关联假设后,选取所有MN个当前关联假设(在假设树的第N+1层)中概率最大的一个,保留以其第2层父结点为根结点的子树,并删除其他结点,维持整棵假设树的深度为N。假设树剪枝后,叶子结点共有MN-1个,对应了k时刻的假设,而唯一的根结点对应了k-N+1时刻的唯一假设,因此,在k时刻可以将根结点对应的估计输出,作为k-N+1时刻关联和跟踪的结果。
1.2 IMM算法原理
1984年,Blom[5]在广义伪Bayes算法的基础上提出了一种具有Markov切换系数的多模型滤波器,其中多个模型并行工作,模型间基于一个Mark-ov链进行切换,目标状态为多个滤波器交互作用的结果。IMM算法滤波的过程可以分为以下几步:
(1)模型交互作用:


图2 IMM-MHT单步关联滤波流程

1.3 基于IMM的MHT算法
将IMM应用于MHT算法,单步关联和滤波的过程如图2所示。
2 仿真结果及分析
2个目标的初始状态分别为:

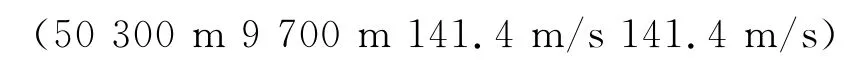
两者保持恒定速率运动,先沿直线运动20s,再向右以18°/s的角速度作匀速转弯运动10s,再沿直线运动10s,再向左以18°/s的角速度作匀速转弯运动10s,最后再沿直线运动20s。雷达的检测概率为PD=0.98,测距精度为σr=100m,测角精度为σθ=0.1°,采样间隔为T=1s,杂波密度为λc=1e-7。
IMM模型集使用CV(匀速)模型和Singer模型[9],模型的先验概率为μ0= [0.5,0.5],Markov转移概率矩阵为:

CV模型的过程噪声取为q=100。Singer模型的自相关时间常数为α=1/10,最大加速度为aM=70m/s2,最大加速度概率为pM=0.1,非机动概率为p0=0.7。量测方程使用线性模型,量测噪声协方差由量测精度通过无偏量测转换得到[8]。MHT假设树参数为:M=3,N=3。
量测和真实航迹见图3,基于IMM-MHT算法的跟踪结果如图4所示。

图3 真实航迹及量测图

图4 基于IMM-MHT的目标跟踪
图5是使用CV模型的关联和跟踪结果,图6是使用Singer模型的关联和跟踪结果。可以看出,在目标发生机动时,CV-MHT算法容易跟踪失败;Singer-MHT算法和IMM-MHT算法在目标的机动段有类似的跟踪性能,但对目标的直线段,前者跟踪效果不如后者,而且前者容易导致关联错误。

图5 基于CV-MHT的目标跟踪

图6 基于Singer-MHT的目标跟踪
以相同的参数进行50次Monte Carlo仿真,跟踪过程中目标丢失率、关联错误率、跟踪位置误差均方根(RMSE)等结果如表1所示。
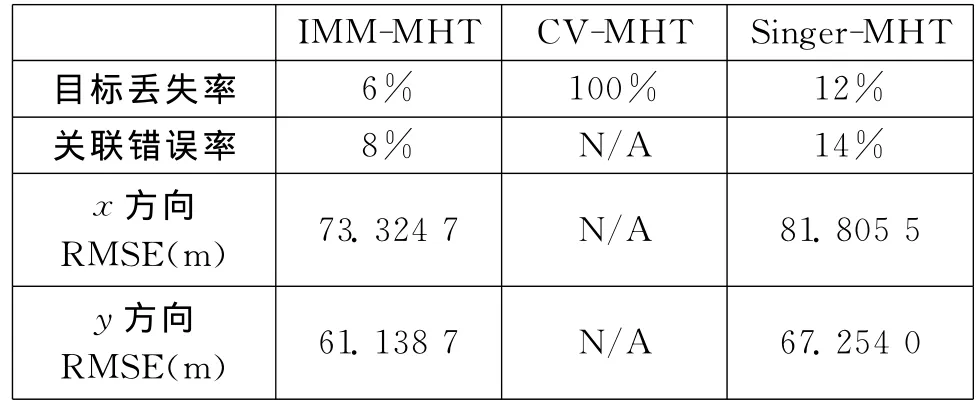
表1 50次仿真的跟踪结果
3 结束语
本文将IMM滤波算法结合到MHT关联算法中,并通过有效的MHT假设生成和假设管理技术,实现了杂波环境下对多机动目标的跟踪,与只采用单模型的MHT算法相比,IMM-MHT算法具有更好的跟踪稳定性和跟踪精度,仿真结果表明了这一算法的有效性。
[1] Singer R A,Sea R G.A new filter for optimal tracking in dense multitarget environment[A].Proceedings of The Ninth Allerton Conference Circuit and System Theory[C].Urbana,1971:201-211.
[2] Bar-Shalom Y,Tse E.Tracking in a cluttered environment with probabilistic data association[J].Automatica,1975,11(9):451-460.
[3] Formann T E,Bar-Shalom Y,Scheffe M.Sonar tracking of multiple targets using joint probabilistic data association[J].IEEE Journal of Oceanic Engineering,1983,8(3):173-183.
[4] Reid D B.An algorithm for tracking multiple targets[J].IEEE Transactions on Automatic Control,1979,24(6):843-854.
[5] Blom H A P.An efficient filter for abrupt changing systems[A].Proceedings of The 23rd IEEE Conference on Decision and Control[C],Las Vegas,1984:656-658.
[6] Cox I J,Hingorani S L.An efficient implementation of Reid's multiple hypothesis tracking algorithm and its evaluation for the purpose of visual tracking[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1996,18(2):138-150.
[7] Murty K G.An algorithm for ranking all the assignments in order of increasing cost[J].Operations Research,1968,16(3):682-687.
[8] 韩崇昭,朱洪艳,段战胜.多源信息融合[M].第2版.北京:清华大学出版社,2010.
[9] 何友,修建娟,张晶炜,等.雷达数据处理[M].第2版.北京:电子工业出版社,2009.
