基于聚类划分子种群的多种群遗传算法

丁若冰，邹书蓉

(成都信息工程学院计算机学院，成都 610000)

引 言

美国的Holland教授在20世纪七十年代首次提出了一种模拟达尔文进化论的自然选择机制的优化算法，是最早的遗传算法起源。遗传算法［1］同其它优化算法相比较拥有隐含的并行性、寻优过程快速、本身的自适应性及其鲁棒性等优点，此外还具有搜索不依赖于问题的梯度信息、模型特征的优点，使其在传统搜索方法难以解决的复杂和非线性问题上有很好的效果，近年越来越多的国内外学者致力于遗传算法的研究，特别是多种群遗传算法的研究。多种群遗传算法(Multi-Population Genetic Algorithm，MPGA)是在遗传算法并行运算的基础上，通过多种群并行进化的思想，将遗传算法中单种群进化过程分解为多个子种群并行进行的过程，每个子种群单独完成选择、交叉、变异操作，这样不仅可以加快算法的收敛速度，而且避免了单个种群进化过程中出现的过早收敛现象［2-6］。

但是，由于传统的多种群遗传算法只是简单地将主种群没有任何规律地划分成多个子种群，所以算法仍存在许多不足之处，如进化后期种群同质化现象严重、种群陷入局部最优等问题。本文提出了一种基于聚类划分子种群的多种群遗传算法(Multiple Population Genetic Algorithm Based on Clustering Dividing Populations，MPGA_BC)，使得子种群划分不再是一种随机行为，而是将满足约束条件的个体根据其特征划分到不同子种群中，从而解决种群同质化问题，避免所有子种群陷入局部最优，从而提高算法性能和算法搜寻全局最优解的能力。

多种群遗传算法后期子种群同质化严重一直是一个重要缺陷，因为同质化会导致种群陷入局部最优，从而不能获得全局最优，尽管变异算子能在一定程度上打破这种状况，但其几率比变异操作的概率还要小得多，本文提出的基于聚类划分的多种群遗传算法从根本上解决种群同质化问题，从而使得算法能最大程度地获得全局最优解。实验结果表明改进的算法有较好的寻优能力和收敛能力。

1 聚类的定义和数学模型

1.1 聚类的定义

聚类［7］就是按照一定的要求和规律对事物进行区分和分类的过程，在这一过程中没有任何关于分类的先验知识，仅靠事物间的相似性作为类属划分的准则，因此属于无监督分类的范畴。“人以群分，物以类聚”，聚类是一个古老的问题，它伴随着人类社会的产生和发展而不断深化，人类要认识世界就必须区别不同的事物并认识事物间的相似性。

1.2 聚类的数学模型

从数学的角度来刻画聚类划分可以得出以下模型:设 X={x1，x2，...，xm}是待聚类分析的对象的全体，X中的每个对象(称为样本)xi(i=1，2，...，m)常用有限个参数值来刻画，每个参数值刻画xi的某个特征。于是对象 xi就伴随着一个向量 P(xi)=(xi1，xi2，...，xis)，其中 s是维度，xij(j=1，2，...，s)是 xi在第 j个属性上的赋值，P(xi)称为xi的特征向量或模式矢量。聚类分析就是分析论域X中的m个样本所对应的模式矢量间的相似性，按照样本间的亲疏关系把 x1，x2，...，xm划分成多个不想交的子集 X1，X2，...，Xc，并要求满足下列条件:

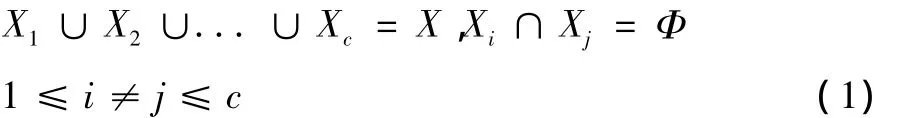
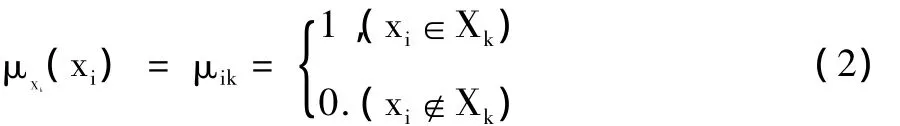
式(2)中，隶属函数必须满足条件μki∈Eh。也就是说，要求每一个样本能且只能隶属于某一类，同时要求每个子集(类)都是非空的。

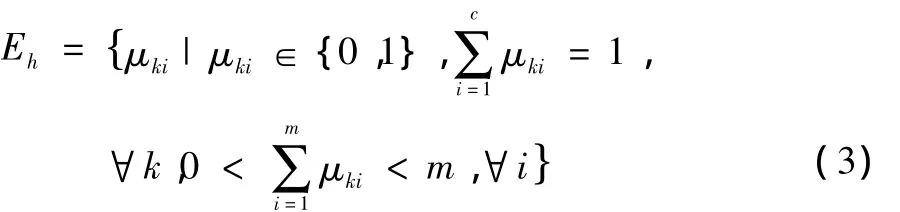
本文使用K均值聚类算，算法详细法描述如下:

(1)随机地生成K个聚类中心;

(2)计算所有样本点到各聚类中心的距离，并将其归入与其距离最近的聚类中心所代表的的那一类;

(3)对每一类，计算其样本均值，将其作为该类新的聚类中心;

(4)如果在第(2)步某一样本的类别发生改变，则转第(2)步;

(5)返回聚类核心和各个样本类别，聚类终止。

2 聚类划分子种群的多种群遗传算法

2.1 引入聚类方式划分子种群优势

传统的多种群遗传算法虽然能够将种群分割，从而加快种群收敛速度，但是传统的划分子种群的方法只是如图1所示，简单随机的将种群初始化为A、B和C几个子种群，并没有按个体本身特性分配到不同种群中去。这样会导致种群同质化严重，最终收敛向同一个最优解。

本文提出引入聚类的思想如图2所示，将特性相似的个体划分到相同的子种群里，这样可以克服基本多种群遗传算法的缺陷，避免种群间出现同质化的现象，而子种群划分能使单个种群更快的收敛到最优解，最后通过子种群间比较取得全局最优，将遗传算法本身的并行性发挥出来，实现并行搜索最优，汇总取全局最优的方式来寻找全局最优的解。此外，使用聚类的方式划分子种群更加符合自然规律［7-8］。

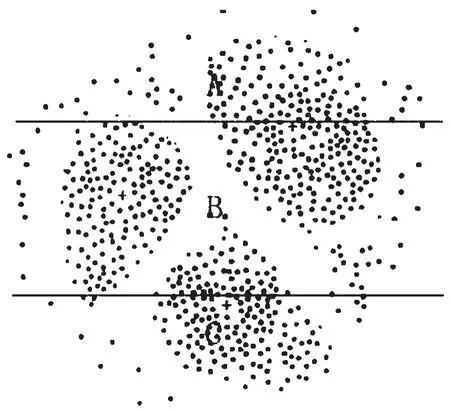
图1 非聚类方式划分样本子种群

2.2 算法步骤

Step0:初始化种群规模P，子种群个数K，以及终止迭代代数T;

Step1:随机生成规模为P的种群;

Step2:将所有个体进行聚类，生成K个子种群;

Step3:对每个子种群进行如下进化迭代:

(1)评价所有个体;

(2)利用最优保留策略的比例完成该子种群父代个体的选择，并对其执行交叉操作;

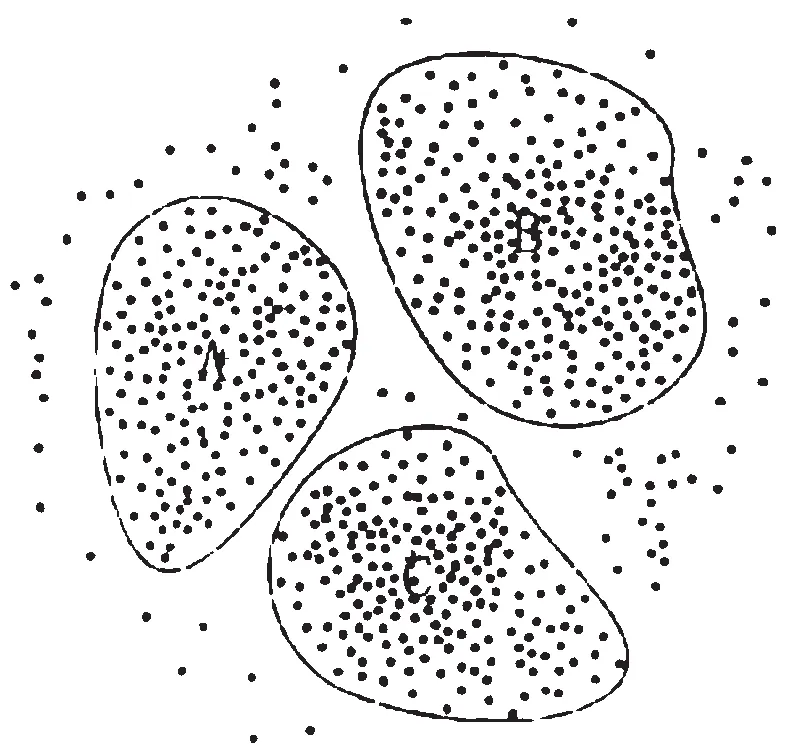
图2 聚类方式划分样本子种群

(3)根据变异概率对种群内个体进行变异操作，得到新一代种群;

(4)如果没有达到给定迭代代数，转Step3，否则，转Step4;

Step4:如果不满足终止条件，将所有子种群合并，转Step2，否则，转Step5;

Step5:从每个子种群中选出最好个体作为最优解，进化过程结束。

3 实验仿真及结果分析

3.1 典型测试函数

为了验证文章中提出的改进的多种群遗传算法的可行性与有效性，选择了两个典型函数Sphere Model与Rastrigrin进行测试，这个两个函数分别表示如下:

Sphere Model函数:

Rastrigrin函数:

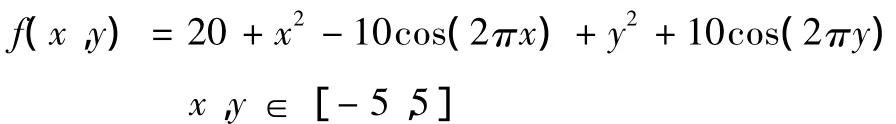
图3和图4分别描述了上述单峰值函数和多峰值函数定义域内的三维图。由图3可知，单峰值函数在f(0，0)时取得全局最优解［图4显示的是一个多峰值典型测试函数的曲面图，有多个峰值陷阱，能够导致一般优化算法陷入局部最优，其全局最优解在x，y∈(0，0)处取得，全局最优解为0。

3.2 测试结果分析

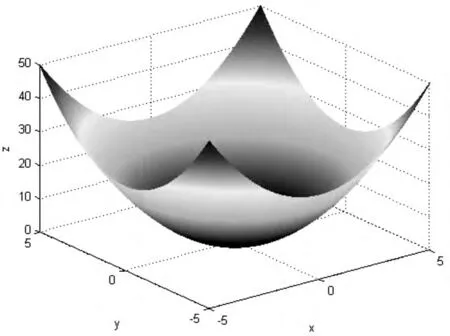
图3 Sphere Model函数三维图

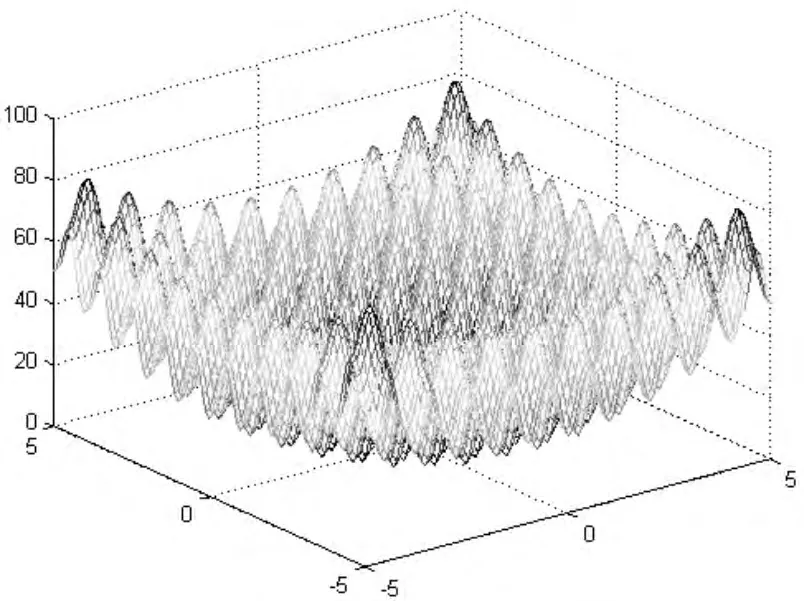
图4 Rastrigrin函数三维图

本实验是在intel i3处理器、4 G内存的个人笔记本上完成的，仿真环境为matlab2013b。实验参数配置见表1。

表1 配置参数列表

表2是两种算法测试对比数据，表明在单峰值函数中，两种算法收敛到全局最优解的次数和搜索到最优解的平均值没有太大差别，改进的算法只是有略微的优势;但是在多峰值函数问题中改进的算法仍然能保持算法收敛率，而传统算法收敛率只有50%左右。在处理复杂的多峰值问题时传统的多种群遗传算法容易陷入局部解、不能收敛、寻找不到最优解等问题。从数据对比可以看到文章提出的算法不仅能够提高收敛率和收敛速度，而且能够在面对复杂的多峰值寻优问题的时候更加稳定的搜索到全局最优解。

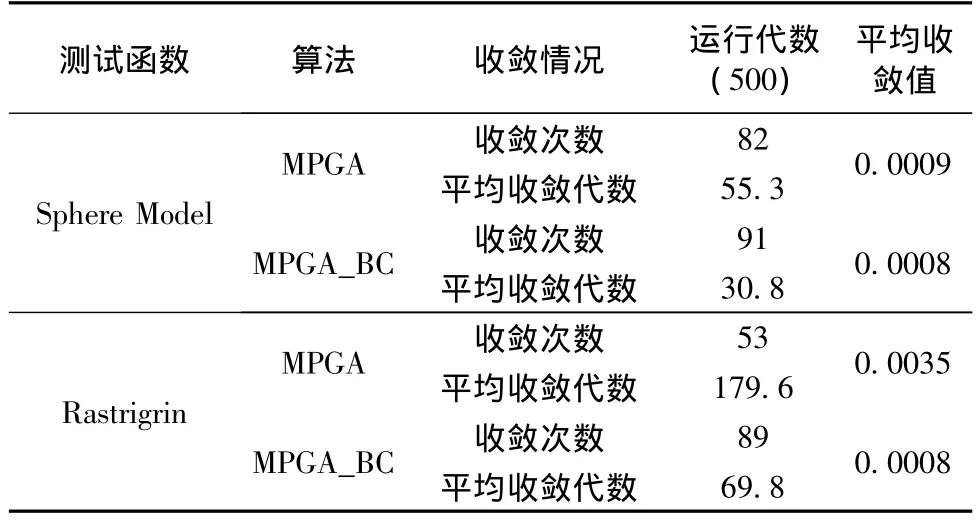
表2 实验数据对比表

4 结束语

本文将聚类划分引入多种群遗传算法，提出了一种使用聚类方式划分子种群的多种群遗传算法，用个体特性来为其归类的思想初始化总群，并将其合理划分为有各自特性的子种群。通过对典型测试函数的实验测试，其结果表明基于聚类划分种群的多种群遗传算法与基本多种群算法相比能够有效的避免子种群陷入同质化现象，能够提高算法收敛率和收敛速度，此外，基于聚类划分子种群的多种群遗传算法相比传统的多种群遗传算法能够更好的搜索到全局最优解，算法有很好的效果。

［1］ Holland J H.Adaptation in natural and artificial systems［M］.Ann Arbor:The University of Michigan Press，1975.

［2］李军华，黎 明，袁丽华.一种改进的双种群遗传算法［J］.小型微型计算机系统，2008，29(11):2099-2102.

［3］Borisovsky P，Dolgui A，Eremeev A.Genetic algorithms for a supply management problem:M IP-recombination VS greedy decoder［J］.Science Direct，2007，19(5):770-779.

［4］公茂果，焦李成，杨咚咚.进化多目标优化算法研究［J］.软件学报，2009，20(2):271-289.

［5］巩敦卫，孙晓燕.变搜索区域多种群遗传算法［J］.控制理论与应用，2006，23(2):256-260.

［6］王文义，秦广军，王若雨.自适应的多种群并行遗传算法研究［J］.计算机工程与应用，2006，42(15):34-36.

［7］孙吉贵，刘 杰，赵连宇.聚类算法研究［J］.软件学报，2008，19(1):48-61.

［8］赖玉霞，刘建平.基于遗传算法的K均值聚类分析［J］.计算机工程，2008，34(20):200-202.