大型风力机柔性叶片在运行工况下的内力分析
2014-04-25李德源
徐 磊,李德源
(广东工业大学机电工程学院,广州 510006)
引 言
单机大型化是现代风力机发展的必然方向,但柔性构件(如叶片等)振动对于机组气动力的影响及与之相对应的气动载荷变化对机组气动弹性的反馈成为不能忽略的问题。在叶片设计过程中,需要准确地知道叶片各截面在空气动力、重力与惯性力作用下的内力,因此,寻求包含非线性变形效应的风力机叶片各截面内力分析的方法成为了大型风力机柔性叶片强度与刚度校核与优化设计的重要基础[1-2]。
对于风力机叶片这种具有空间运动和弹性变形的构件,Molenaar[3]及 Holierhoek[4]等人引入“超级单元”(Superelement)对其进行离散,以反映其弹性变形。Molenaar[3]采用超级单元(无扭转自由度)对风力机的柔性构件(如风轮叶片和塔架)进行离散,各刚体之间通过力元(弹簧、阻尼器)与铰连接,这样风力机系统可以用一离散的刚、柔混合多体系统(HMBS)来表示。Holierhoek[4]使用HMBS方法建立了 NM80风力机的力学模型,利用哈密顿原理导出了动力学方程,分析了超级单元个数及几种不同的计算超级单元弹簧系数的方法对柔性件的固有频率和阻尼系数计算精度的影响。
对于叶片空气动力载荷的计算,目前常用的理论有叶素动量理论(Blade Element-Momentum Theory,BEM)、广义动态尾流理论(Generalized Dynamic Wake Theory,GDW)以及计算流体动力学(Computational Fluid Dynamics,CFD)方法等[5]。由于 BEM 理论求解快速,且可结合其他非定常气动模型,计算结果合理,应用较广。GDW理论除了计算旋转平面到尾流的轴向诱导速度外,还考虑了尾迹效应,气动模型较为复杂[6]。而CFD方法则使用数值方法求解非线性微分方程组(Navier-Stokes方程)[7],虽然计算精度较高,但计算量较大。
本文采用HMBS方法建立叶片多体系统的力学模型,基于虚位移原理导出了该系统的动力学方程的一般形式,编制了通用的动力学仿真程序。在此基础上联合BEM气动模型得到气弹耦合模型,在对动力学方程进行数值积分每一时间步中,气动模型能实时地根据叶片各刚体的速度、角速度和姿态坐标(方向余弦阵)计算出作用在叶片各刚体上的气动载荷,并将其加载到瞬时变形的叶片中,实现了叶片的气弹耦合时域响应分析。
算例以美国可再生能源实验室(NREL)发布的5 MW近海风力机叶片为研究对象[8],计算了风力机叶片在运行工况下挥舞、摆振与扭转力矩的时域响应。所作研究对大型风力机叶片设计、优化与保障风力机组的安全稳定运行,具有重要的应用价值及意义。
1 柔性叶片的多体系统动力学建模
应用计算多体系统动力学中的Roberson-Wittenburg(R-W)方法[9]来建立柔性叶片的多体动力模型。为了准确地描述叶片在气弹耦合分析中表现出的柔性行为,在多体系统模型中引入所谓的“超级单元”对柔性叶片进行动力学建模[4],并将变形较小的轮毂和机舱等构件处理为刚体[10],可在尽量少的自由度下得到与实际相符的结果。每个超级单元包含4个体,单元之间通过相邻体联接,而单元内部体通过带弹簧和阻尼器的万向节或转动铰相联接,使其能反映叶片的横向弯曲变形与扭转变形。这样叶片被处理成由刚体、铰、力元和外力组成的多体系统。
1.1 超级单元模型和叶片的离散
将柔性构件离散为若干个超级单元,如图1所示。其中B1和B2,B3和B4均由万向节连接,而B2和B3则由旋转铰连接,由此来反映构件的弯曲与扭转变形,弹簧与阻尼器约束刚体间的相对运动(如图中的Cy1~Cy3)。因此,每个超级单元有4个旋转和1个扭转共5个自由度,图1中两个相互垂直平面内的弯曲由2个万向节的广义坐标 θ1,θ2,θ4,θ5来表示,扭转则由转动铰的广义坐标θ3来表示。

图1 超级单元模型
以NREL 5 MW水平轴风力机61.5 m长叶片为算例,将其离散为4个超级单元来建立柔性叶片的拓扑模型。由于前后两个超级单元中相邻的两刚体刚性联接,可合并为一个刚体(如B4、B7和B10),这样叶片可分割成13个刚体,共21个自由度。在地面上建立惯性坐标系XYZ,在叶片的根部建立叶片坐标系X'Y'Z'(叶片的挥舞和摆振状态的参考坐标系),OO'的距离与轮毂质心到叶根的距离相同,以模拟叶片绕风轮主轴的转动。
1.2 柔性叶片的多体系统动力学方程
根据R-W方法,按照规则标号对图2所示的多体系统中各个体及铰进行标号,体记作Bi(i=1,…,13),其内接铰记作Hi(i=1,…,13)。铰H1的铰点建立在惯性坐标系原点O上,其余内接铰Hi的铰点均建立在各刚体质心截面的弦长1/4处。以B1代表叶片上与轮毂固结的刚体,其运动被约束,对于其余体Bi,其内接铰Hi的相对运动可通过固结在体Bi及其内接体上的坐标系的相对关系来描述。

图2 刚体规则标号、惯性坐标系XYZ和叶片坐标系X'Y'Z'
取各铰的转动为广义坐标,则从柔性叶片多体系统的拓扑构形可得其广义坐标阵为:


式中,k为质点系质点数[rk为质点广义坐标;δrk为其虚位移;为广义加速度;Fk为外力主矢与主矩构成的广义力。由此可导出叶片系统以q(t)为变量的二阶常微分方程组:

其中,Z称为广义质量阵;z为广义力阵,其具体表达形式可参阅文献[9]。该方程组中广义质量和广义力阵均包含了以广义坐标q为变量的方向余弦阵,而且这些变量随时间变化,因此该方程组呈非线性。结合相应的初始条件,对上式进行数值积分求解,即可求得叶片中各个体的运动量q(t)、(t)及(t)。
1.3 模型的相关参数与模型验证
柔性叶片离散为通过弹簧盒阻尼器连接的多个刚体的过程中,关键问题在于弹簧的刚度系数如何确定才能使模型能尽量符合柔性叶片的力学特性,确定原则如下:(1)在静载荷下,离散模型的弹性变形应和柔性叶片变形相等[(2)超级单元应与相同尺寸的刚性梁有相同的质量和惯性性质[(3)超级单元的固有频率应尽量接近连续梁的固有频率。
NREL发布的5 MW近海风力机为上风向变速变桨距风力机,叶片截面刚度分布、质量分布与翼型等参数及各截面翼型气动特性等参数可参考文献[8]。据弹性梁的弯曲与扭转理论[4],可得各超级单元中弹簧的刚度系数(表1)。

表1 NREL-5MW风力机叶片弹簧刚度系数/(Nm/rad)
针对本文叶片多体模型,应用多体动力学软件ADAMS/Vibration对该叶片的固有频率进行了计算,结果与NREL提供的基于风力机气弹分析软件FAST的分析结果进行对比(表2),验证了本模型的有效性。

表2 计算结果对比
2 叶片气动载荷计算与气弹耦合分析
运用叶素-动量理论(BEM)计算作用在叶片各刚体上的气动力,并采用普朗特叶尖修正[5]。假设某刚体Bi(i=1,…,13)各截面处的气动载荷相同,并始终作用在Bi质心截面的气动中心处(叶片质心截面弦上距前缘1/4处,如图3)。则由叶素理论,风轮平面内某一环形区域所受的推力FT及转矩Q计算公式为:


图3 刚体Bi质心截面上的气动参数及气动中心连体基
由动量理论,风轮平面内某一环形区域所受的推力FT及转矩Q计算方法为:
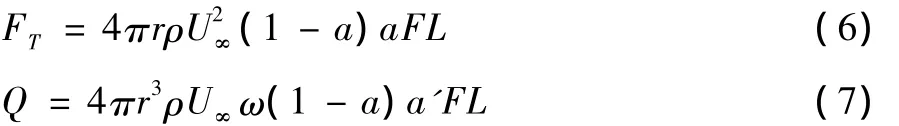
其中,r为气动中心距离旋转中心的距离;B为风轮叶片数;ρ为空气密度;c为Bi的质心截面处叶素的弦长;U∞为来流风速;ω为风轮旋转角速度;W为作用在刚体Bi质心截面气动中心切向速度ωr与来流风速U∞的合速度;α为刚体Bi质心截面处的攻角;L为刚体Bi沿叶片径向的长度;CL、CD和CM分别是升力系数、阻力系数和力矩系数,它们为攻角α的函数;a为轴向诱导因子;a'为切向诱导因子;F为叶尖损失因子。
当叶片变形较大时,考虑叶片变形与挥舞与摆振速度对气动力的影响,入流角φ及攻角α的计算公式为:

其中,φ为空气入流角;θ为叶素的扭转角;Ve-op为气动中心挥舞速度;Ve-ip为气动中心摆振速度。
结合以上公式,以及二维翼型升阻特性数据,便可通过迭代的方法计算出所需要的物理参数。具体迭代步骤可参考文献[11]。
气弹耦合仿真是在多体系统动力模块的基础上增加气动载荷计算模块来实现的,耦合仿真流程如图4所示。仿真过程中如果当前时刻t小于仿真时间tend,则多体动力学模块将会在每一个时间步中调用气动模块计算时变的气动载荷。这些气动载荷作为外力输入到多体系统动力学模块计算出下一时间步中改变了的叶片各刚体的姿态坐标(方向余弦阵)、速度和角速度,这些参数再输入到气动模块,从而可计算出下一时间步的气动载荷并再次耦合到叶片的结构动力学计算去,如此循环直到时间终点。

图4 气弹耦合分析流程图
建立约束方程限制叶片转速

其中q1为叶片相对于机舱的转动自由度,ωe为额定转速12.1 r/min。对于变转速控制,此处亦可采用非线性约束方程进行约束。仍采用违约稳定法计算叶片的动力学响应。文中取α =β=10,仿真时间为50 s,积分精度为10-5。
3 算例分析
3.1 模型及其参数的选取
基于以上的建模基础,对文献[8]提供的5 MW风力机叶片在随机风速下的气弹响应进行了数值分析。计算过程在随机风速及额定转速(12.1 r/min)下进行。
考虑到此风轮直径(126 m)较大,叶片上各刚体(叶素)在不同的高度风速存在风剪,引入风速随高度变化的公式加以修正:

式中,V、V0为距地面高度分别为H及H0处的平均风速,本文中,取V0=11.4 m/s,为轮毂高度H0=90 m处的风速;α为切变系数或粗糙度指数,是一个经验指数,其值为0.125 ~0.6,文中取 0.16。
3.2 叶片的内力分析
叶片变形导致相邻两个刚体之间产生相对转动,因此刚体之间截面上的内力可通过刚体间的力元(弹簧、阻尼器)进行计算,弹簧力和阻力分别与刚体之间的相对转动角度和转动速度成正比。
图5为叶片各刚体间的挥舞力矩图。从中可以看出,叶片挥舞力矩为正(与风速方向相同),其中叶根处挥舞力矩最大(B1与B2之间)。挥舞力矩由空气动力载荷、重力载荷与惯性力所导致,由于风力机在运行过程中,始终受到随机来流的压迫作用;同时,各刚体的加速度也随时间不断变化,造成了挥舞力矩的波动。

图5 叶片各刚体挥舞力矩
图6为各刚体间的摆振力矩。从中可以看到,在风力机运行过程中摆振力矩一般为负(与风轮旋转方向相同),这是由于叶片始终受到升力的作用。而在这一过程中,叶片变形产生的结构弹性力与气动力相互影响,导致叶片的摆振力矩作周期性的波动。
图7为叶片超级单元(共4个)内的扭转力矩。从中可以看到,在风力机运行过程中扭转力矩一般为负,这是由于叶片各刚体气动中心偏离扭转轴,而刚体始终受到来流风所引起的空气阻力的作用。
图8为叶尖的运动轨迹。如图8所示,由于叶片的预弯作用,故叶尖的初始点不在零点。由图8可以看出,当风力机工作在工况下时,叶尖在气动力及结构力的相互作用下,始终在一定范围内不断颤动。
4 结束语
本文应用超级单元法将柔性叶片离散为有限个体,并应用R-W建模方法,建立柔性叶片的非线性代数-微分气弹耦合方程,结合BEM计算叶片的空气动力和适当的数值求解方法,用不多的自由度,实现了大型风力机叶片的非线性气弹耦合时域响应分析。算例对5 MW的风力机在紊流风速下的非线性气弹响应进行了数值模拟。

图6 叶片各刚体摆振力矩

图7 叶片各超级单元内的扭转力矩

图8 叶尖在垂直于叶片径向的平面内的运动轨迹
柔性叶片非线性多体动力学气弹耦合方程的构建与数值求解可通过编制的软件由计算机完成,大大节省建模与求解方程的时间以及可能引起的差错。通过建立不同的约束条件,可以实现变速或定转速风力机的时域分析。应用该方法,可以分析叶片上各位置处的截面内力,进而进行叶片的强度、刚度分析和气弹稳定性分析。通过时域响应的频域分析,也可以实现叶片动力特性如固有频率、结构阻尼与气弹阻尼等与气弹稳定性相关的分析,分析的精度可通过增加超级单元的个数进行调整。在叶片设计或优化阶段,仅需通过输入文件,调整输入参数就能得到不同的优化结果。
基于时域响应的大型风力机叶片气弹耦合分析,对于大型风力机叶片的优化设计和安全稳定运行具有重要的意义,也是进行叶片气弹稳定性分析的重要基础。本文的工作对于叶片强度与刚度校核与优化设计有重要的应用价值。
[1] Hansen M O L,Sørensen J N,Voutsinas S,et al.State of the art in wind turbine aerodynamics and aeroelasticity[J].Progress in Aerospace Sciences,2006,42(4):285-330.
[2] Kallesoe B S.Effect of steady deflections on the aeroelastic stability of a turbine blade[J].Wind Energy,2011,14:209-224.
[3] Molenaar D P.Cost-effective design and operation of variable speed wind turbines[D].Delft:Delft University of Technology,2003.
[4] Holierhoek J G.Aeroelasticity of Large Wind Turbines[D].Delft:Delft University of Technology,2008.
[5] Hansen M O L.Aerodynamics of wind turbines[M].2nd ed.UK:Earthscan,2008.
[6] Kim S,Sclavounos P D.Fully coupled response simulations of theme offshore structure in water depths of up to 10000 feet[C]//Proceedings of 11th International Offshore and Polar Engineering Conference(ISOPE),Stavanger,Norway,June 17-22,2001:457-466.
[7] Meng F Z.Aero-elastic Stability analysis for largescale wind turbines[D].Delft:Delft University of Technology,2011.
[8] Jonkman J,Butterfield S,Musial W,et al.Definition of a 5-MW reference wind turbine for offshore system development[R].Springfield:U.S.National Renewable Energy Laboratory,2009.
[9]洪嘉振.计算多体系统动力学[M].北京:高等教育出版社,1999.
[10] Gebhardt C G,Preidikman S,Jørgensen M H,et al.Non-linear aeroelastic behavior of large horizontalaxis wind turbines:A multibody system approach[J].International Journal of Hydrogen Energy 2012,37(19):14719-14724.
[11] 李 春,叶 舟,高 伟,等.现代陆海风力机计算与仿真[M].上海:上海科学技术出版社,2012.
