基于EMD与1D全变分的地震信号去噪
2014-04-25王均荣安素珍周仲礼王茂芝
王均荣,张 涛,安素珍,周仲礼,王茂芝
(1.成都理工大学数学地质四川省重点实验室,成都 610059;2.电子科技大学神经信息教育部重点实验室,成都 610054)
引 言
地震信号中噪声的压制是地震数据处理中重要的预处理任务,关系到后续的地震信号属性提取和数据解释等相关工作。严格意义上地震信号属于非平稳信号[1],随着现代地震勘探对地震资料信噪比的要求越来越高,各种现代数字信号处理方法被广泛应用,如ICA、PCA、小波阈值、EMD、TV等去噪方法。但是,目前很多方法难以有效地应付更为复杂的地震信号,往往在去噪的同时,也会造成严重的细节性有效信号的丢失。因此,在有效消除地震信号噪声的同时,如何有效保持地震信号中的构造边缘信息,已成为人们更为关心的问题。经验模态分解时频分析法是最近发展起来的一种处理非线性非平稳信号的新方法,由于EMD算法能自主分解输入信号,因此EMD去噪是自适应的,不需要先验知识,与传统的傅里叶变换滤波相比有着明显的优势[2]。另外,1D-TV算法能较好地实现地震信号与噪声信号的分离,并能有效的保护地震信号边缘信息[3-4]。
将EMD技术与1D-TV方法相结合,应用于地震信号噪声的压制。首先通过EMD算法将地震信号分解为一系列表征信号特征时间尺度的固有模态函数(Intrinsic Mode Function,IMF),然后应用1D-TV方法对所选择的高频成分IMF分量进行处理,最后利用处理后的IMF分量重构信号,从而达到去噪的目的。该方法能充分发挥两者的优点,在更精细的尺度上对噪声进行压制,并使信号边缘信息得到有效的保护。实际的地震数据处理结果表明该新算法是可行的,且去噪效果优于单独使用EMD方法。
1 EMD/TV(全变分)方法原理
1.1 经验模态分解(EMD)去噪原理
EMD是对非平稳信号进行时频处理的方法,该方法将信号中不同尺度的波动逐级分解开来,产生一系列具有不同特征尺度的数据信号,每一个数据信号就是一个固有模态函数[5]IMF,IMF分量按从高频到低频依次排列。其中,IMF必须满足以下两个条件:
(1)信号的极值点数目和过零点数目相等或最多相差一个。
(2)且由局部极大值构成的上包络线和局部极小值构成的下包络线的平均值为零[6]。
以实际地震信号分解(图1)为例,EMD算法的实施步骤:
(1)找到信号y(t)所有的局部极大值并且用三次样条函数插值连接,获得上包络线[同理,连接局部极小值点作为下包络线。
(2)上下包络的平均值组成均值信号m,并定义信号h1=y(t)-m。
(3)如果信号h1满足IMF的条件,那么h1就是求得的第一个IMF分量;否则将h1作为原始信号进行(1)~(2)的步骤,直到第k次迭代后的差值成为第一个IMF,记为 c1。
(4)从原信号中减去c1,得到第一阶剩余信号r1=y(t)-c1,将r1作为新数据序列重复上述过程,可以递推得到其他IMF,直到趋势分量rn单调或只有一个极值。

图1 原始地震信号通过EMD分解成不同的IMF成分
假设 y=(y[1],···,y[N])∈RN,N > 1,采集到的地震信号,x=(x[1],···,x[N])∈ RN为干净的地震信号,n为采集过程中混入的随机噪声,则

其中,x(t)为干净信号,n(t)为噪声信号,对y(t)进行EMD分解后满足下式:

其中,ci为第i个IMF分量,rn+1为剩余分量。
EMD去噪的基本原理是从分解的IMF分量中去除高频噪声引起的IMF分量。由于EMD分解的IMF分量从高到低,因此第一个IMF分量的频率最高,是由高频随机噪声引起的。去除高频分量后,用剩余的IMF分量重构信号,即达到去噪的目的[5,7]。
1.2 1D-TV模型去噪原理
全变分去噪模型首先由Rudin、Osher and Fatemi于1992年提出[8],主要用于图像的去噪、修复、分割等方面,该方法基于噪声图像的全变分明显高于无噪声图像的全变分,把图像去噪问题转化为求解图像模型的能量泛函最小化问题,其实质就是各向异性扩散,从而实现去除图像的噪声,其优点在于平滑噪声的同时,又能很好的保持图像边缘特性[9-10]。
对于式(1)给出的噪声信号,其全变分的离散形式定义为[3]:

由于噪声图像的全变分明显要大于无噪声图像的全变分,因此全变分的信号去噪问题就转化为最小化全变分泛函问题[12]:
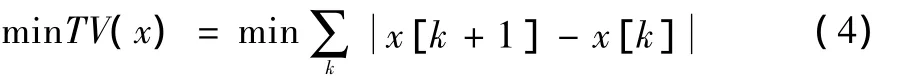
其可以等价于式(5),即为求解非线性最优化问题[3-4]:

式(5)中,第一项为保真项,它主要起降低原信号失真度的作用;第二项为正则化项,λ为正则化参数,λ的取值与信号的噪声水平有关,对平衡去噪与平滑起重要作用。
本文采用Little[11]提出的原始-内点对偶算法来求解,通过在原始信号上加上高斯白噪声进行仿真实验(图2)。从图2可以看出,经1D-TV处理后,噪声得到很好的压制。
2 新算法的构造
为了更好地去除地震信号中的噪声,同时保护地震构造边缘信息,基于1D-TV算法和EMD算法各自的优点,提出了一种新的混合去噪算法,其基本思想:首先,通过EMD算法将地震信号分解为一系列表征信号特征时间尺度的固有模态函数IMF;然后,应用1D-TV方法对所选择的高频成分IMF分量进行处理;最后,利用处理后的IMF分量重构信号,从而达到去噪的目的。
2.1 EMD分解高频部分确定原则

图2 1D-TV去噪效果
信号经EMD分解后得到有限个频率从高到低的IMF,其中阶数小的IMF对应于信号的高频成分,一般包含的是信号尖锐部分或噪声,阶数大的IMF对应于信号的低频成分,一般认为低频成分中的噪声影响很小。基于EMD去噪的主要思想就在于,对大多数被噪声污染的信号,其主要能量集中在低阶IMF段,越往高阶 IMF段,其含的能量就越小[5,7]。因此,一定存在某个IMF分量,使得对于该分量之后的IMF(k+1)中的信号为主导模态,而其前k个IMF中噪声为主导模态。
对于含有噪声的地震信号表达式可以写成:

式中s(t)为干净地震信号,m(t)为噪声信号。现采用噪声能量最小的准则重构地震信号,用˜(t)表示EMD分解信号得到的本征模态函数重构得到的地震信号。去掉前k-1个本征模态函数后的信号:

利用均方差[13]使˜(t)尽量接近s(t)。均方差表示为:
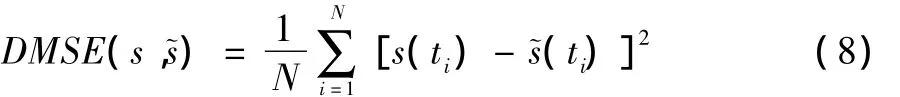
依据公式(8)可得IMF组中各个分量的能量:

由此求得能量最小分量对应的k值,则有:

式(11)中,n是重构地震信号的起始IMF索引,从第n个本征模态函数开始,以后的都为信号的主要成分,从而确定k值。
2.2 新算法的描述
对地震信号y(t)去噪混合算法描述如下:
Step1:将地震信号y(t)进行多尺度EMD分解,得到一组从高频到低频排列的本征函数IMF。
Step2:根据上述能量法则选取前k阶IMF作为高频信号。
Step3:对选取的高频信号进行选取不同的正则化参数λ进行1D-TV去噪。
Step4:对处理后的高频IMF成分和剩余IMF成分进行重构得到去噪后的地震信号。
其流程如图3所示。

图3 EMD-1DTV去噪算法流程图
3 实际地震信号处理
利用新提出的算法,对某一金属矿床地震信号行了处理。图4为含有噪声的原始地震剖面图,此地震数据是二进制格式,选取了100道,道间距50 m,每道500个采样点,采样间隔为1 ms。图5为利用新提出的基于EMD+1DTV方法去噪后的地震剖面图,图6为传统EMD方法去噪后的地震剖面图。
为了评价提出的新算法信号去噪的效果,利用峰值性噪比(PSNR)和边缘保持度两个评价标准对实际的处理结果进行评价[14]:
(1)峰值信噪比:


图4 原始地震信号波形图

图5 EMD+1DTV方法去噪后的地震信号波形图

图6 EMD方法去噪后的地震波形图
其中,q(i,j)为原始的地震数据,p(i,j)为经过处理后的地震数据;(i,j)为地震数据中的某一点;M,N代表地震数据中点的集合。
(2)边缘保持度[15]:

其中,EPI为边缘保持度,p(i,j),q(i,j)分别为处理后的地震数据和原始地震数据的某一点。EPI为去噪后的地震数据和未经去噪的地震数据的边缘对比度之比,EPI越接近于1,去噪后的地震信号边缘保持度就越好。
通过表1可以看出,基于EMD与1DTV的新算法对金属地震资料处理结果要比单独的运用EMD效果要好,在峰值信噪比和边缘保持度上都有着很大的提高。

表1 峰值信噪比与边缘保持度处理结果对比表
4 结束语
EMD和全变分方法都是新兴的信号处理方法,EMD分解对信号有良好的自适应性,而全变分方法在信号降噪的过程中能保护好信号的边缘信息,有着广泛的应用,但是二者也有各自不同的缺陷,并不完美,因此把二者有效的结合具有十分重要的理论与实践意义。关于一维全变分在处理一维信号上还有很多的限制,因此,对一维全变分在地震信号上的处理还值得进一步的研究。
[1](美)L科恩.时频分析理论及应用[M].白居宪,译.西安:西安交通大学出版社,1998.
[2]杨凯,刘伟.基于改进EMD的地震信号去噪[J].西南石油大学学报:自然科学版,2012,34(4):75-81.
[3] Karahanoglu F I,Bayram I,Van D V D.A signal processing approach to generalized 1-D total variation[J].Signal Processing,IEEE Transactions on,2011,59(11):5265-5274.
[4] Condat L.A direct algorithm for 1D total variation denoising[J].IEEE Signal Proc.Letters,2013,20(11):1054-1057.
[5]史恒,李桂林,王伟,等.基于总体经验模式分解的地震信号随机噪声消除[J].地球物理学进展,2011,26(1):71-78.
[6] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of The Royal Society A Mathematical Physical and Engineering Sciences,1998,454(1971):903-995.
[7]王 婷.EMD算法研究及其在信号去噪中的应用[D].哈尔滨:哈尔滨工程大学,2010.
[8] Rudin L I,Osher S,Fatemi E.Nonlinear total variation based noise removal algorithms[J].Physica D:Nonlinear Phenomena,1992,60(1):259-268.
[9] Chan T F,Golub G,Mulet P.A nonlinear primal-dual method for total variation-based image restoration[J].SIAM J.Sci.Comp.,1999,20(6):1964-1977.
[10] Chambolle A,Lions P L.Image recovery via total variation minimization and related problems[J].Numer-ische Mathematik,1997,76(2):167-188.
[11]Little M A,Jones N S.Sparse Bayesian step-filtering for high-throughput analysis of molecular machine dynamics[C]//Proceedings of the IEEE International Conference on Acoustics,Speech,and Signal Processing,Dallas,Texas,USA,March 14-19,2010:4162-4165.
[12] Tang G,Ma J W.Application of Total-Variation-Based curvelet shrinkage for Three-Dimensional seismic data denoising[J].IEEE geoscience and remote sensing letters,2011,8(1):103-105.
[13] Boudraa A O,Cexus J C.EMD-Based signal filtering[J].IEEE Transactions on Instrumentation and easurement,2007,56(6):2196-2202.
[14]屈 勇,曹俊兴,朱海东,等.一种改进的全变分地震图像去噪技术[J].石油学报,2011,32(5):815-819.
[15]钟勇,孙东,陈磊.图像增强技术在地震资料处理中的应用[J].物探与化探,2010,34(3):392-341.
