远探测声反射成像测井裂步式傅里叶法偏移成像

肖承文，李军孝，吴兴能，徐明，张承森，王贵清，陶果

（1.中国石油塔里木油田分公司勘探开发研究院，新疆 库尔勒 841000；2.中国石油大学地球物理与信息工程学院，北京 102249；3.中国石油渤海钻探工程有限公司测井分公司，天津 300280）

0 引 言

地震勘探的分辨率低、常规声波测井径向探测深度浅等问题导致其对小型地质构造不能有效勘探开发。远探测声反射成像测井作为一种新型的测井技术，相比地震勘探有较高的分辨率，相比常规声波测井具有较深的横向探测深度，可以探测井外10～20 m范围的地质构造以及对井外地质情况进行探测和评价［1－5］。

反射波提取及偏移成像算法是利用反射声波测井资料对井旁构造进行探测评价的关键。国内外学者对反射声波测井偏移成像方法做了大量的研究。Hornby［6］利用f－k滤波成功将反射信号与直达波信号分离并成像。Coates［7］经过数据处理得到了水平井中的成像重构图，但文献没有介绍所应用的方法。Chabot［8］将等效偏移距偏移方法（EOM）应用到了声反射测井数据中，此外，还利用Pro MAX地震资料处理软件对实际的井资料作了处理，成像重构结果显示了井旁倾斜地层倾角。王乃星［9］利用长源距全波列测井数据提取出了反射信号，从而达到探测井旁裂缝走向及倾角的目的。李长文等［10］对反射声波数据进行了处理分析，但没有对偏移成像方法作详细的介绍。Zhang Tiexuan，Tao Guo等［11］将EOM方法应用在声反射资料偏移成像处理中，解决了声反射成像测井资料覆盖次数低的问题，有效提高了信噪比，但是该方法无法适应横向速度变化剧烈的速度模型。

中国石油渤海钻探工程有限公司测井分公司于2009年研发了远探测声反射成像测井仪器［12］，开发的处理软件系统（ARI）成功应用叠前Kirchhoff偏移成像［13－14］得到了井旁地质体构造。尽管积分方法叠前深度偏移具有能够对目标区进行选择性成像、高效灵活等优点，但是由于它的基础是把Kirchhoff积分中的格林函数用高频近似解（射线理论解）来代替，因此在实际应用中存在一定的局限［15］。局限之一是Kirchhoff积分法的分辨率会随着深度的增加而逐渐变差，从而导致对深层构造的成像精度变低，这一现象源于利用射线解近似格林函数时菲涅尔带的影响。局限之二是Kirchhoff积分法缺乏正确的振幅信息，在复杂介质中通常会有多重路径和波的干涉等现象，利用射线法很难在这种介质中获得正确的振幅信息。理论上波动方程法叠前深度偏移能够弥补Kirchhoff积分法的不足。

裂步傅里叶叠前深度偏移方法在较复杂地质条件下是一种快速稳定的波动方程叠前深度偏移方法，在当前地震数据叠前深度偏移中应用较为广泛。它也是基于传统的单程波方程实现的，最早由Stoffa提出［16］。该方法基于速度场分裂的思想，把整个速度场视为常速背景和变速扰动叠加。在逐层波场延拓时，针对常速背景采用相移处理，在频率－波数域实现，而针对层内的变速扰动，则在频率－空间域采用时移校正。该方法继承了相移法的优点［17－18］，即没有倾角限制和频散的影响，也能适应速度场的中等程度的横向变化，且与相移法深度偏移比，每层在计算上仅多出1次反傅里叶变换和1次时移校正，计算量增加不大。本文主要将该方法应用于远探测声反射测井成像处理中，并通过数值模拟数据以及实际井资料处理验证了该方法的准确性。

1 裂步傅里叶偏移算法原理

裂步傅里叶偏移方法主要应用在频率－波数域，在偏移距和空间变化的扰动项中通过定义参考纵波值，这个参考纵波值在相位偏移中作为常速度，应用在频率－波数域，通过深度距向下进行数据传播。扰动项用来定义震源，这个震源是通过频率－波数域中的第2相位移加以考虑的。裂步傅里叶方法有相移法的优越性也能调整横向速度的变化，通过定义参考慢度和扰动项，很好地解决了速度横向变化的问题。

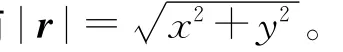
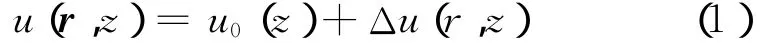
式中，u0（z）为参考慢度，即平均慢度。慢度的一切变化都归入Δu（r，z）分量中，由声波方程可得到

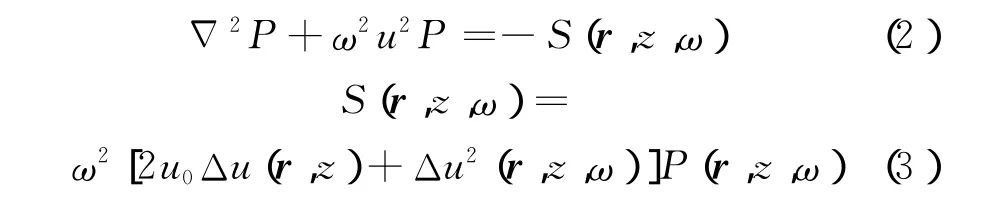
慢度扰动项S（r，z，ω）的引进，将均匀介质的声波方程转换为非均匀介质的声波方程。为求解方程（2），首先将深度zn上已经偏移的上行波场P＿（r，zn，w）进行从r到k r空间的傅里叶变换

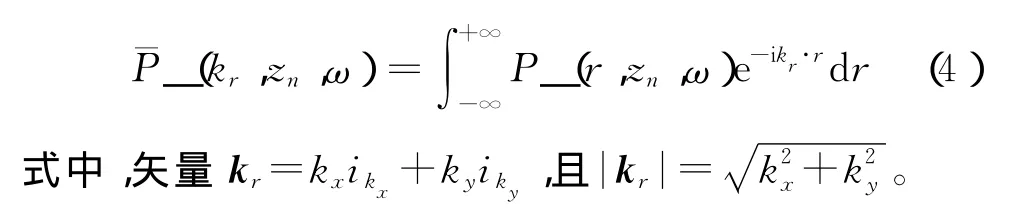
根据由参考慢度计算的垂向波数，对所有频率的波数作相移

在层段Δz内施加由慢度中存在的扰动Δu（r，z）＝u（r，z）－u0（z）所引起的第2次相移

第1次相移与常速相移偏移相同，而第2次相移相当于加入一个校正项，它根据各空间位置上的实际慢度与参考慢度之差提供的时移校正值确定。与其他偏移方法一样，在下一个偏移层段重复该过程。这样就可以得到整个深度段的成像结果。

对于普通地震资料偏移，建立一个较准确的初始速度模型对于裂步傅里叶偏移成像结果精确与否至关重要。相比地震数据，在远探测声波测井数据的裂步傅里叶偏移中，由于声波资料信噪比高，由其得到的速度曲线能较好地反映相应深度的地层速度，且远探测声波测井横向探测深度一般小于20 m，因此由该速度曲线建立的速度模型比较精确。因此，将裂步式傅里叶偏移应用到远探测声波测井是可行的，且可以有效回避地面地震中低信噪比、初始速度模型不准等问题。

2 数据处理

为了验证裂步式傅里叶积分在声反射成像测井中应用的准确性，利用ARI软件分别对数值模拟数据和实际数据处理。

2.1 数值模拟

首先给出1组模拟数据，图1（a）所示为一井旁裂缝带，由3条平行排列的单裂缝组成，裂缝开度为10 cm。裂隙填充流体密度与井内流体密度一致。模型大小为6 m×15 m，井眼位于横向深度0 m处。井眼、裂缝与地层参数如表1所示。

表1 模型井眼流体、裂缝以及地层纵横波速度和密度

图2（a）所示为交错网格有限差分数值模拟得到的关于如图1（a）所示模型的全波列，最前面幅度最小的为滑行P波，中间幅度较小的为滑行S波，后面幅度最大的为斯通利波。由于相对于反射波而言，模式波的能量很强，因此在全波列中几乎看不到反射波。通过去除全波列中的模式波，就可以得到理论的反射波场，如图2（b）所示。

图1 数值模拟模型和偏移结果

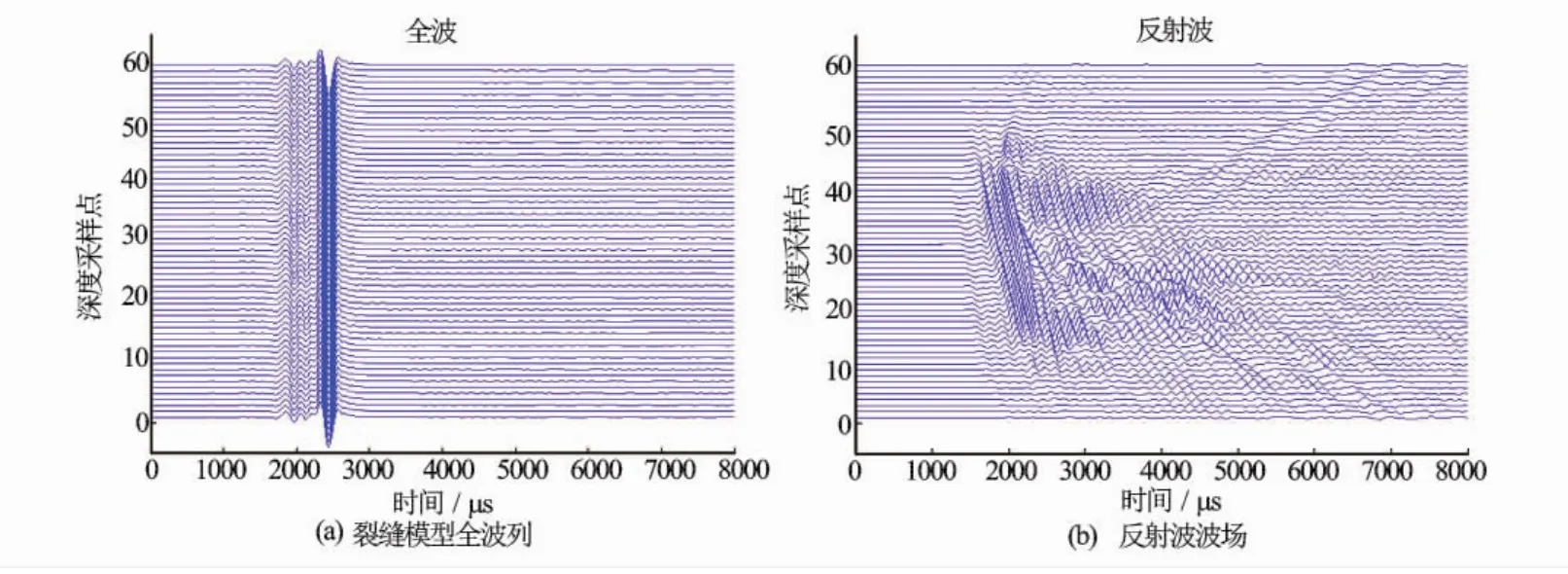
图2 交错网格有限差分数值模拟得到的裂缝模型波场

用沿着模型井眼底部到顶部采集到的60个深度点的反射波形记录进行裂步式傅里叶偏移成像，得到如图1（b）所示的成像结果。从结果图上可以清晰看到靠近井轴的2条单裂缝，其横向深度和垂向深度都与模型一致，从而充分证明了裂步式傅里叶偏移在声反射成像测井中的准确性。对该反射波数据作了Kirchhoff偏移成像，结果如图1（c）所示，成像结果只显示出了靠近井轴的1条单裂缝，且与模型相比，裂缝的角度也有所不一。值得注意的是，第3条裂缝没有出现在裂步式傅里叶偏移结果图上，这是由于波场透过前2条裂缝后，又透射到第3条单裂缝上，再通过2次透射才能传到井轴，而经过多次反射和透射后，波场能量已经大幅衰减，因此成像结果只能显示出前2条单裂缝。

2.2 实际数据

经过模拟数据的论证，进一步分析实际测井数据以验证裂步式傅里叶偏移的正确性。并且还将处理结果与开发的远探测声反射成像测井处理软件（ARI）旧版的Kirchhoff偏移结果作对比，充分证明了裂步式傅里叶偏移的优越性。

图3为一实际井某深度段常规曲线以及SSF成像结果图。图3中，GR曲线值显示该层段为砂岩层段，电阻率值也相对较高，表明该层段是很好的储层。利用远探测声反射成像测井仪器接收到的声波数据分别作了Kirchhoff偏移成像（旧版软件）以及裂步式傅里叶偏移（旧版软件）处理。从图3上可以看到，Kirchhoff偏移成像得到的结果中，井旁反射体主要在泥质含量比较大的层段，但是由于泥质含量的影响，该层段的反射体往往不是井旁裂缝、孔洞等构造引起的；不同于Kirchhoff偏移成像结果，在裂步式傅里叶偏移成像算法中，考虑了泥质含量对成像结果的影响，从图像上可以看到，在泥质含量比较高的井段（×05～×25），裂步式傅里叶偏移算法很好地压制了由泥质含量造成的成像假象，且在泥质含量相对较小的层段，也就是在×30～×50层段，裂步式傅里叶偏移成像结果显示有较清晰的井旁反射体，但是Kirchhoff偏移成像结果显示在该段没有井旁反射体。根据综合解释，该层段孔隙发育良好，实际生产中，该层段日产油达到118.1 m3，日产气16 216 m3。这表明裂步式傅里叶偏移结果更优于Kirchhoff偏移成像结果。

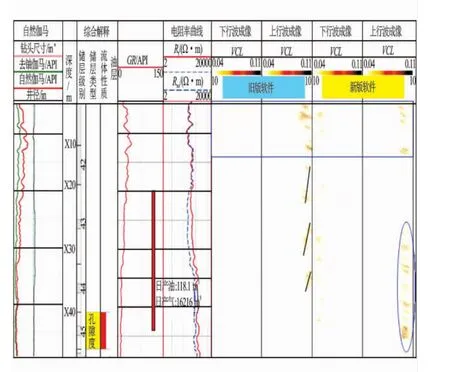
图3 实际井数据Kirchhoff偏移成像结果与裂步式傅里叶偏移成像处理结果

3 结 论

基于地震领域中的裂步式傅里叶偏移方法，针对远探测声反射成像测井作相应的改进，没有倾角限制和频散的影响，能适应速度场的中等程度的横向变化，是一种能有效识别井旁地质体的偏移成像算法。通过数值模拟数据以及实际资料的处理结果验证了该方法的有效性。

［1］ Hornby B.Imaging of Near－borehole Structure Using Full Waveform Sonic Data［J］.Geophysics，1989，54（6）：747－757.

［2］ Esmersoy C，Chang C，Kane M，et al.Acoustic Imaging of Reservoir Structure from a Horizontal Well［J］.The Leading Edge，1998，17（7）：940－946.

［3］ Hirabayashi N，Torii K，Yamamoto H，et al.Fracture Detection Using Borehole Acoustic Reflection Survey Data［J］.SEG Technical Program Expanded Abstracts，2010，29（1）：523－527.

［4］ Tang X，Zheng Y，Patterson D. Processing Array Acoustic－logging Data to Image Near－borehole Geologic Structures［J］.Geophysics，2007，72（2）：E87－E97.

［5］ Wang B，Tao G，Wang H，et al.Extracting Near Borehole P and S Reflections from Array Sonic Logging Data［J］.Journal of Geophysics and Engineering，2011，8：308－315.

［6］ Brian E Hornby.Imaging of Near－borehole Structure Using Full Waveform Sonic Data ［J］.Geophysics，1989，54（6）：747－757.

［7］ Esmersoy C，Chang C，Kane M，et al.Acoustic Imaging of Reservoir Structure from a Horizontal Well［J］.Leading Edge，1998，17（7）：6－12.

［8］ Chabot L，Henley D C，Brown R J，et al.Single－well Imaging Using the Full Waveform of an Acoustic Sonic［C］∥ SEG Annual Meeting，San Antonio，Texas，2002.

［9］ 王乃星，苏华，刘文明，等.声波全波列测井中反射波成像分析 ［J］.测井技术，1998，22（4）：278－283.

［10］李长文，余春昊，赵旭东，等.反射波信息在裂缝储层评价中的应用 ［J］.测井技术，2003，27（3）：198－202.

［11］Zhang T X，Tao G.Application of the Equivalent Offset Migration Method in Acoustic Log Refection Imaging［J］.Applied Geophysics，2009，6（4）.

［12］柴细元，张文瑞，王贵清，等.远探测声波反射波成像测井技术在裂缝性储层评价中的应用 ［J］.测井技术，2009，33（6）：539－543.

［13］Gray S H，May W P.Kirchhoff Migration Using Eikonal Equation Travel Times ［J］.Geophysics，1993，59：810－817.

［14］Li J X.，Tao G，Wang H，et al.An Effective Data Processing Flow for the Acoustic Reflection Image Logging［C］∥ 74th Conference ＆ Exhibition，EAGE，2012.

［15］牟永光，陈小宏，刘洋，等.地震数据处理方法 ［M］.北京：石油工业出版社，2007：146－183.

［16］Stoffa P L，Fokkema J T，De Luna Freire R M，et al.Split－step Fourier Migration ［J］.Geophysics，1990，55（4）：410－421.

［17］Gazdag J.Wave Equation Migration with the Phaseshift Method［J］.Geohpysics，1978，43：1342－1351.

［18］Gazdag J，Sguazzero P.Migration of Seismic Data by Phase－shift Plus Interpolation［J］.Geophysics，1984，49：124－131.

［19］Loewenthal D，Lu L，Robertson R，et al.The Wave Equation Applied to Migration ［J］.Geophys Prosp，1976，24：380－399.