基于储层孔喉特征参数计算致密砂岩渗透率的新方法
2014-09-18成志刚罗少成杜支文常森李戈理李华
成志刚,罗少成,杜支文,常森,李戈理,李华
(1.中国石油集团测井有限公司,陕西 西安 710077;2.长庆油田公司采气五厂,内蒙古 乌审旗 017300)
0 引 言
非均质性严重的致密砂岩储层渗透率变化大,即使考虑不同沉积相带,利用传统方法通过拟合岩心分析的渗透率与孔隙度得出一个经验关系,其相关系数并不高,有时甚至没有相关性,无法准确预测渗透率。利用核磁共振测井数据计算储层渗透率的经典Coates模型和SDR模型,以T2分布谱为基础,通过T2截止值的选取计算渗透率[1-2]。而T2截止值的选取受很多因素的影响[3],存在一定的误差,因而无法保证渗透率的计算精度。为解决利用核磁共振测井数据计算储层渗透率时存在的问题,本文根据压汞和核磁共振测井T2分布均反映储层孔隙结构的事实,利用核磁共振T2谱构建伪毛细管压力曲线求取表征孔隙结构定量参数,结合地区经验,优选参数,构建能表征渗透率的δ函数进行渗透率预测,取得了较好的应用效果。
1 传统孔隙度与渗透率关系模型
××井区岩性致密,根据岩心物性资料统计,孔隙度主要分布在2%~9%,平均4.4%;渗透率分布在(0.05~10)×10-3μm2,峰值在0.05×10-3μm2。按照传统的孔隙度和渗透率拟合方法进行拟合,其拟合效果很差,几乎没有相关性(见图1)。

图1 常规物性孔隙度和渗透率关系图
2 核磁共振计算渗透率的常用模型
确定核磁共振渗透率的方法是以T2分布为基础,通过T2截止值的选取计算可动流体以及束缚流体的体积,然后利用SDR、Coats-cutoff、Coats-SBVI、SDR-Reg模型等4种经验公式计算渗透率[4]。

式中,φNMR为核磁共振测井计算的孔隙度,%;T2g为T2几何平均值,ms,其计算公式为T2g=;φNMR,m为由T2谱分布计算得到的可动流体体积,%;φNMR,b为由T2谱分布计算得到的不可动流体体积,%;K1、K2、K3、K4分别为4种模型计算的核磁共振渗透率,×10-3μm2;C1、C2、C3、C4、m、n为待定系数,由岩心实验分析确定。
对××井区10口井58块岩心样品进行了核磁共振实验测量,分别确定了C1、C2、C3、C4及m、n等待定参数,采用这4种模型计算了岩心的核磁共振渗透率,分别与常规方法测量的空气渗透率进行比较,图2为这4种公式计算的渗透率与空气渗透率比较的直观显示。图2中各点与对角线越接近,说明核磁共振计算渗透率精度高;反之,说明核磁共振渗透率计算的精度越低。
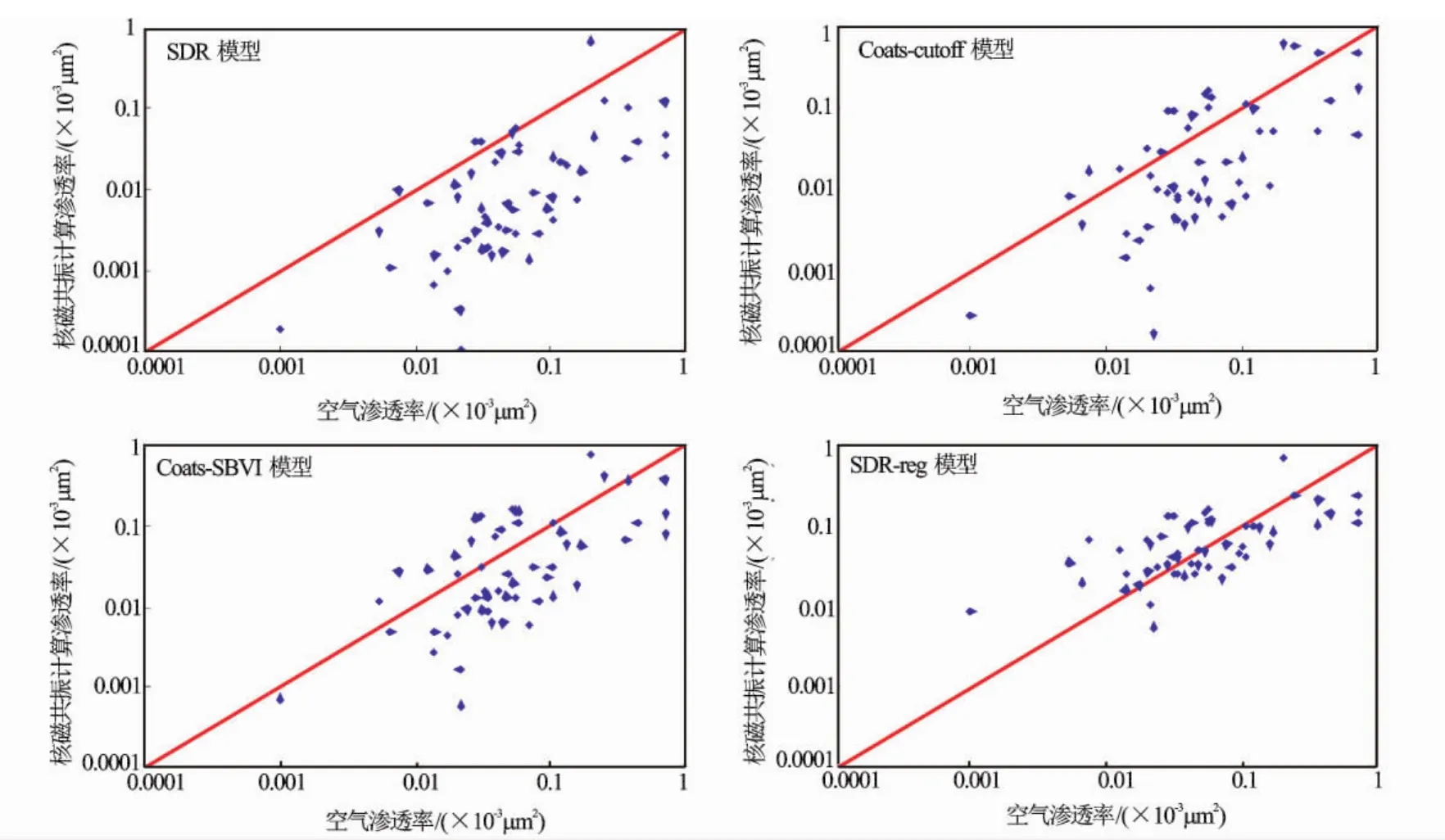
图2 核磁共振计算渗透率与空气渗透率对比图
上述确定核磁共振测井渗透率的方法均依赖于T2截止值,而T2截止值尚无方法准确计算出,造成核磁共振渗透率模型不能很好地表征致密砂岩储层的渗透率。从图2可见,其核磁共振渗透率计算的精度并不高,平均绝对误差分别为0.186×10-3、0.168×10-3、0.178×10-3μm2和0.168×10-3μm2。计算结果与实验分析空气渗透率存在着一定的偏差。
3 基于压汞和核磁共振测井T2分布的渗透率模型的建立
核磁共振测井所表达的经典渗透率模型主要依据岩石连通孔隙的宏观总体积刻画其渗透性,在致密砂岩储层中,具有相同孔隙度的岩石渗透率可以相差很大,关键是它们的孔隙结构差异,其中不同大小孔隙及其与喉道的相互搭配关系是影响渗流能力的主要因素[5],因此,提出以压汞和核磁共振测井为基础,首先利用核磁共振T2谱构建伪毛细管压力曲线,求取表征孔隙结构定量参数,然后优选参数,构建能表征渗透率的δ函数,再结合实际的核磁共振测井资料实现连续的渗透率计算。
3.1 核磁共振T2谱构建伪毛细管压力曲线
根据核磁共振测井响应机理及毛细管压力理论,在简化的线性刻度下T2与pc之间关系[6]为

式中,pc为毛细管压力,MPa;T2为横向弛豫时间,ms;C为转换系数,无量纲。
转换系数C一般通过岩心刻度得到,具体方法采用相似对比法[7]。图3(a)是核磁共振T2谱横向转换后与实测毛细管压力曲线对比效果图。为得到不同毛细管压力情况下进汞饱和度增量,必须将经过横向转换系数刻度后的伪毛细管压力曲线幅度增量经过刻度转换为进汞饱和度增量,具体方法采用分段等面积刻度确定纵向转换系数D1和D2[8]。图3(b)是核磁共振T2谱纵向转换后的孔喉分布频率与实测对比效果图。从图3可见,转换效果有很好的一致性。

图3 核磁共振T2谱转换为伪毛细管压力曲线对比图
为实现在无压汞测量资料的情况下能够有效利用核磁共振T2谱定量计算毛细管压力曲线,必须提出一种与压汞测量资料无关的横、纵向转换系数计算方法。经过多次统计分析,建立了C、D1、D2的统计关系模型

3.2 参数优选
由于孔隙结构特征参数类型多,不同孔隙结构特征参数之间的关系并不完全一致,利用单一的孔隙结构特征参数反映储层孔隙结构类型与渗透率的关系误差较大。为此,从所有孔隙结构参数中优选出能够充分反映储层渗透率的特征参数,根据优选出来的孔隙结构特征参数构建1条综合曲线表征渗透率。结合地区经验和实验测试资料的统计分析,排驱压力和主流喉道半径与渗透率相关关系好(见图4)。孔隙度和渗透率是宏观表征储层物性的参数,预测渗透率模型孔隙度也必须考虑。
3.2.1 排驱压力(pd)

图4 排驱压力、主流喉道半径与渗透率关系图
排驱压力(pd)是指非润湿相(汞)开始进入岩样所需要的最低压力,它是汞开始进入岩样最大连通孔喉而形成连续流所需的启动压力,也称为阈压或门槛压力,在毛细管压力曲线上是沿着曲线的平坦部分作切线与纵轴相交的压力值。然而在致密砂岩中,其毛细管压力曲线大多没有明显的平坦直线,很难作出它的切线,手工作图也会出现因人而异的现象,且也不利于后期的连续计算。为此,采用三次样条插值方法,将曲线的初始拐点(或突变点)的水平位置定为排驱压力[9]。图5为三次样条插值法计算的排驱压力与实验分析图解法的对比图,其平均绝对误差为1.945MPa。

图5 三次样条插值与图解法的排驱压力对比图
3.2.2 主流喉道半径(Rz)
主流喉道半径(Rz)指喉道对渗透率累积贡献值达95%以前喉道半径的加权平均。Rz越大,储集物性越好。区间渗透率的贡献值即占总渗透率的百分数,可以由式(9)确定[10]

式中,ΔSi-(i+1)为压力pi到pi+1的区间内进汞量,%;(pc)i-(i+1)为i点和i+1点的毛细管压力平均值,MPa;ΔSi为i点的进汞增量,%;(pc)i为i点的毛细管压力值,MPa。
实际计算中,利用式(9)计算出不同喉道区间的渗透率贡献值,然后计算喉道对渗透率累积贡献值达95%以前喉道半径的加权平均值,即为主流孔喉半径Rz。
3.3 渗透率模型的建立
结合上述分析,优选出孔隙度、排驱压力和主流喉道半径为敏感参数,经过多次统计分析,构建了一条综合反映储层渗透性的指示曲线

图6为构建的指示曲线与渗透率的关系图,其相关性好,说明了δ综合指示曲线能够准确、定量表征致密砂岩储层的渗透性,解释模型精度高。
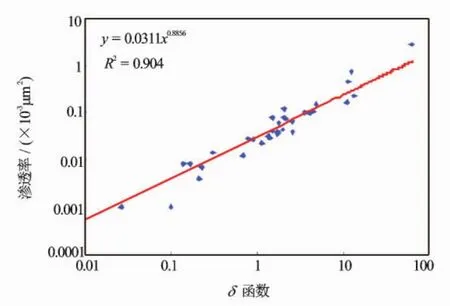
图6 渗透率解释模型
3.4 实际资料处理
利用上述方法建立的模型对××井区进行了实际资料的处理。图7是××井的渗透率预测成果图。图7中第2道为经过烃校正后的核磁共振测井T2谱,第3道为T2谱构建的伪毛细管压力曲线,第5、6道是根据伪毛细管压力曲线计算出的排驱压力和主流孔喉半径,第7道红色杆状图为岩心分析渗透率,蓝色曲线为基于压汞和核磁共振T2谱计算的渗透率值,其计算的渗透率与岩心分析渗透率的误差都在数量级范围内,平均绝对误差为0.0750×10-3μm2(见图8),满足了精细油藏描述的要求,所建立的储层渗透率预测模型十分有效可靠。
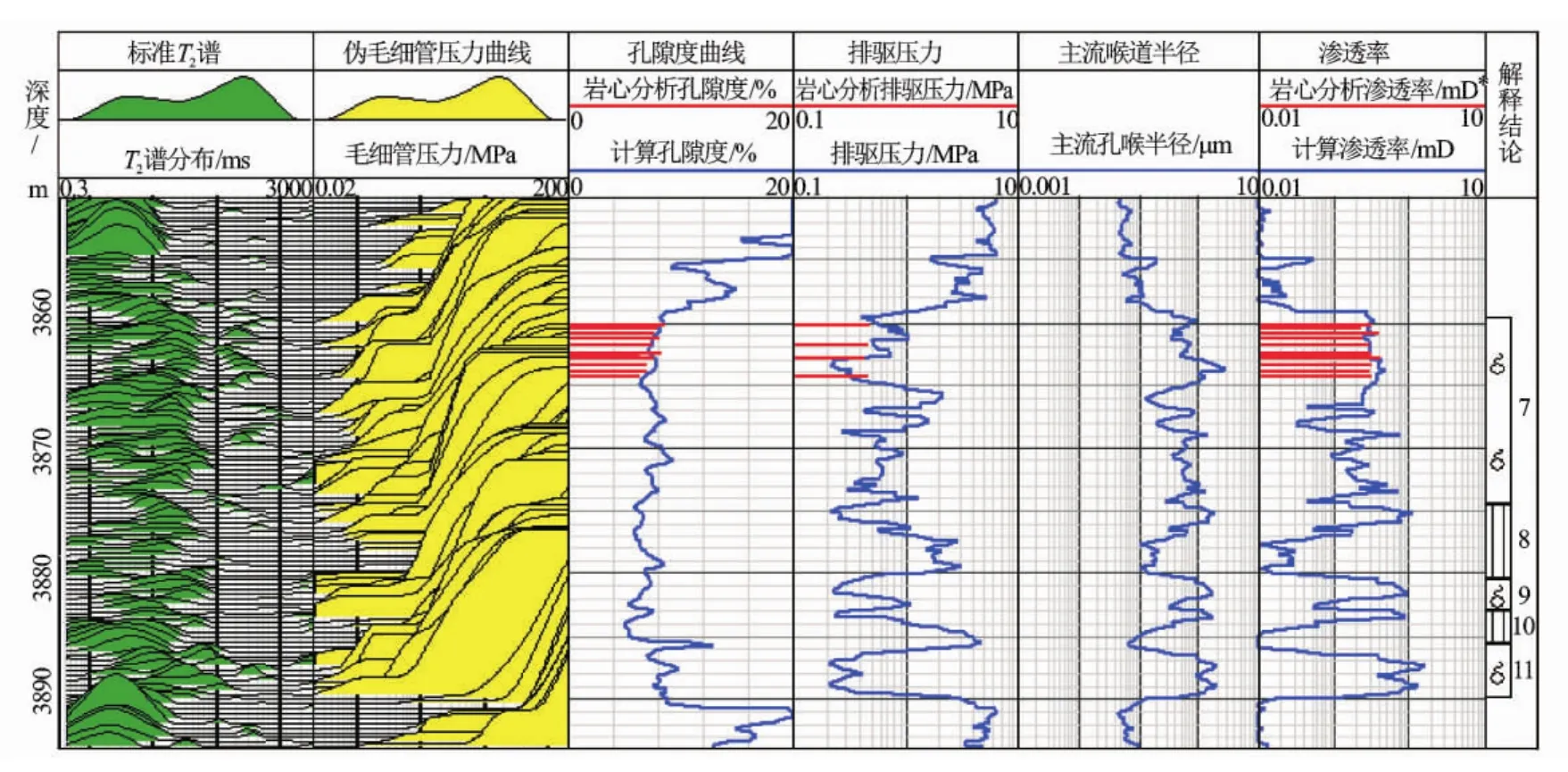
图7 ××井的渗透率预测成果图

图8 计算与实验分析渗透率对比图
4 结 论
(1)利用三次样条插值函数计算排驱压力的方法将毛细管压力曲线的初始拐点的水平位置定为排驱压力。该方法适合于任何形态的毛细管压力曲线,便于计算机的连续处理。
(2)通过对38块岩心样品毛细管压力曲线的定量参数优选,结合××井区的地质特点,选取孔隙度、排驱压力、主流孔喉半径为参数,建立了能反映致密砂岩储层渗透率的表征模型,其模型相关性高且简单。
(3)基于岩心实验分析结果及核磁共振测井T2分布和压汞曲线均反应储层孔隙结构,将T2谱转为伪毛细管压力,求取出排驱压力与主要流动孔喉半径,提出了基于压汞和核磁共振测井快速、连续而准确地计算致密砂岩储层渗透率的方法。
[1]肖立志.核磁共振成像测井与岩石核磁共振及其应用[M].北京:科学出版社,1998:35-62.
[2]周灿灿,程相志,司兆伟,等.核磁共振自旋回波串确定渗透率方法探讨 [J].测井技术,2002,26(2):123-126.
[3]王志战,邓美寅,翟慎德,等.油井样品NMR T2谱的影响因素及T2截止值的确定方法 [J].波谱学杂志,2006,23(1):143-151.
[4]赵文杰,等.核磁共振实验应用研究最新成果 [C]∥第二届中俄测井国际技术交流会议论文集,2002.
[5]付金华,石玉江.利用核磁测井精细评价低渗透砂岩气层 [J].天然气工业,2002,22(6):39-42.
[6]中国石油勘探与生产分公司.低孔低渗油气藏测井评价技术及应用 [M].北京:石油工业出版社,2009.
[7]刘堂宴,王绍民,傅容珊,等.核磁共振谱的岩石孔喉结构分析 [J].石油地球物理勘探,2003,38(3):328-333.
[8]邵维志,丁娱娇,刘亚,等.核磁共振测井在储层孔隙结构评价中的应用 [J].测井技术,2009,33(1):52-56.
[9]胡罡,陆正元,罗平.三次样条插值在排驱压力计算中的应用 [J].新疆石油地质,2004,25(5):544-545.
[10]罗蛰谭,王允诚.油气储集层的孔隙结构 [M].北京:科学出版社,1986.
