瞬变电磁测井原理研究Ⅰ：Doll几何因子

2014-04-23朱留方臧德福沈永进沈建国

测井技术 2014年2期

朱留方，臧德福，沈永进，沈建国

（1.中石化胜利石油工程有限公司测井公司，山东东营 257096；2.天津大学电子信息工程学院功率超声实验室，天津 300072）

0 引言

电阻率测井从电极、侧向到感应测井，分别采用直流电、交流电激发方法。电极和侧向测井依据直流电的基本原理；感应测井依据交流电的基本原理。其激发电信号的频率分别为0和单个频率［1］。阵列感应测井采用方波激发［2］，增加了几个倍频信号。直流电测井所采集到的原始信号是电压和电流，感应测井所采集到的原始信号是正弦波。直流的电压和电流直接反映地层的电阻率［1］，感应测井则通过正弦波的幅度和相位携带地层电导率信息。信息测量方面，现有的直流电测井方法原始测量信号少，交流电测井方法携带地层信息不丰富。阵列声波测井波形［3］和核磁共振测井［4］的原始信号是由各种频率的正弦波或指数衰减波组成的时域波形，对其分别进行频谱分析和解谱计算能够获得相应的频谱，这些频谱信号能够提供更加丰富的地层信息。

为了增加电阻率测井原始信号所携带的地层信息，需要发射多种频率的信号［5］，不同频率的电磁信号在地层中会产生不同的响应，这些响应叠加在一起构成了瞬变电磁测井原始测量波形。对于这些原始测量波形，可以在电磁感应理论［5－6］的指导下设计处理方法，从中提取地层电参数的有效信息。瞬变电磁测井发射瞬变电磁信号，其频谱是以低频为主的连续谱，在井内激发的感应电动势满足电磁感应原理。本文借助于Doll几何因子对其响应进行初步分析。

1 瞬变电磁测井激发的频谱

电法测井仪器中，频率为0的直流电测井工作波形是方波（电极测井最早曾经用机械换向器），以便消除自然电位对直流电响应测量的影响。因为方波的频率低，理论研究仍然采用直流电理论研究其响应。普通感应、双感应、阵列感应和高频感应［5］测井则采用正弦波或方波激发。普通感应或双感应测井时，其激发的正弦波只有1个频率，用模拟电路测量其虚部幅度，在一阶近似的情况下，虚部的幅度与地层的电导率成正比，按照几何因子加权叠加。阵列感应测井则采用方波激发，激发的频率除了基频以外，还有其倍频成分。图1为方波和三角波激发时出现的多个离散频率，图1中绘制了前3个频率对应的幅度。其中3倍频的幅度中方波的幅度比较大，三角波的幅度比较小。这样，阵列感应测井除了测量基频的幅度外，还测量倍频的虚部幅度，相当于1次激发获得了3种频率的响应信号。

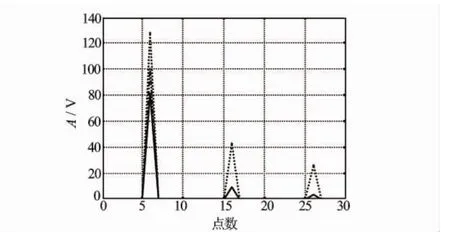
图1 正弦（长虚线）、方波（虚线）和三角波（实线）的频谱

如果用阶跃激励则可以得到连续的多种频率的激发。图2是阶跃函数的频谱1／（iω）。从图2上可以看出，频率越低，其幅度越大。这种激发方式以低频为主，频率越高，激发的幅度越小，所有频率的响应按照频谱加权后相加则构成其阶跃激发的响应，该响应随时间衰减。这种激发方式的频谱是连续的，与现有的感应测井有很大的区别，其携带的地层参数信息贯穿于所测量到的全部响应波形中。

图2 阶跃函数激发的频谱

从普通感应、双感应、阵列感应测井到俄罗斯高频感应测井，其激发的频率从20 k Hz增加到14 MHz。俄罗斯高频感应采用多个不同源距和间距的发射、接收线圈组合［5］，用多种频率的正弦波激发，直接测量2个接收线圈接收到的正弦波的相位差。由于其频率变化范围是875 k Hz～14 MHz，所满足的微分方程为

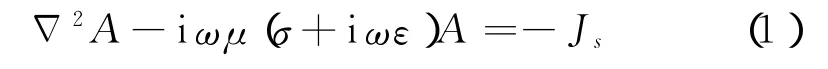
式中，A为描述瞬变电磁场的势函数；ω是角频率；μ、ε分别是地层的磁导率和介电常数；σ是地层的电导率。从式（1）可以看到，括号内有2项，第2项描述电磁波的传播特征，与频率成正比，随着频率的增加，与括号中第1项的电导率（描述电磁感应特征）在数值上逐步接近。这样，在所测量的信号中，传播效应（括号中的第2项，主要导致正弦波的相位移动）和电磁感应（括号中的第1项，主要导致正弦波幅度衰减）效应对响应的影响都存在，都对测量结果有比较大的影响，或者说俄罗斯的高频感应测井仪器可以同时测量到地层的电阻率和介电常数。

当频率再增加时，括号中的第2项大于第1项，测井响应主要由电磁波的传播效应决定，所测量的值主要是相位移动（类似于声波波形），即电磁波的传播速度，通过速度获得地层的介电常数，这时，对应的测井方法是电磁波传播测井。

从以上直流电到感应测井、阵列感应到高频感应以及最后到电磁波测井的发展轨迹可以看出，在过去几十年里，电阻率测井以频率增加为发展方向。激发功率通常比较小，只适合裸眼井测井。

瞬变电磁测井则向频率减小的方向发展，采用阶跃激发或者低频方波激发，发射的功率比较大，激发的频谱是连续的，式（1）中括号内的第1项远远大于第2项，主要利用电磁感应原理，通过测量地层产生的二次电磁场获得地层的电阻率。

2 电磁感应的二次场

从Fourier级数展开或Fourier变换知道，阶跃激发或者低频方波激发函数可以分解成一系列不同频率的正弦波的叠加，用感应测井提供的方法可以研究单个频率的响应，然后按照激发的频谱（为权重）相加即可得到总的响应。因此，瞬变电磁测井也可以看成交流电测井，满足电磁感应原理，主要测量二次场，用Doll几何因子可以对其二次场进行近似描述。

通过分析Doll几何因子推导过程中所涉及到的几个关键问题，进一步理解二次场的概念以及测井响应与地层电导率之间的关系。给出瞬变电磁测井响应中二次场即有用信号的计算方法。

在无限大均匀介质中仅研究单频激发（正弦波Ieiωt）的响应。位于井中心的线圈激发的磁场相当于磁偶极子M＝nTS0Ieiωt（M的方向是z）激发的磁场强度H，其中，S0是激发线圈的面积，I是其中流过的电流幅度，ω是角频率，磁场强度H的矢径方向ρ的分量Hρ为

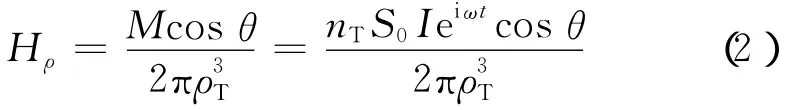
式中，ρT为测点距发射线圈中心的距离；θ为矢径方向与M方向的夹角；nT是激发线圈的圈数（见图3）。

图3 感应测井几何因子推导所用变量示意图

设地层中单元环的半径为r，以发射线圈T的中心为球心，通过单元环作一个球面。在这个球面的法线方向，磁场强度分量由式（2）给出。因为球面上的面积元是dS＝2πρ2Tsinθdθ，所以通过单元环的磁通量Φ是单元环上的球面的电磁感应强度在其法线方向的投影与面积元乘积后的积分，磁感应强度Bρ与磁场强度Hρ之间的关系Bρ＝μsHρ，其中μs是地层的磁导率。则通过单元环上球面的磁通量Φ为

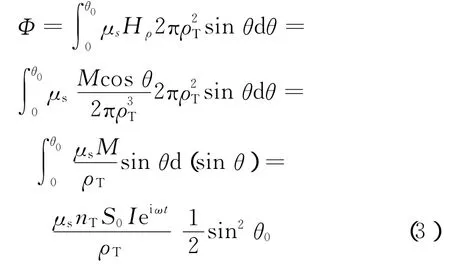
由电磁感应原理知，磁通量对时间的导数等于电动势。单元环上的电动势V为

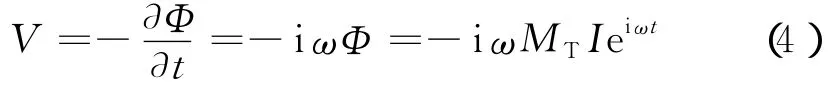
这是一次感应电动势或直接耦合感应电动势，与频率成正比，因为对时间的求导使表达式中出现了频率因子ω。

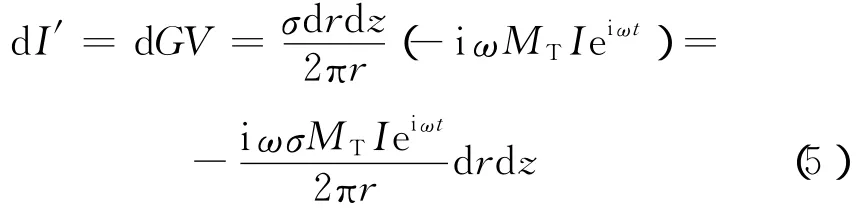
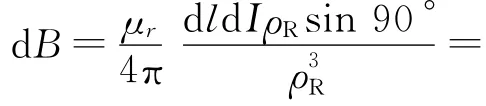
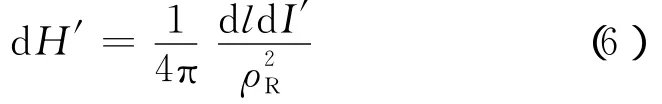
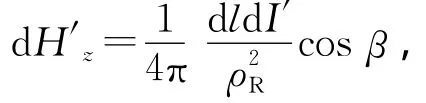
沿单元环积分得到整个单元环在接收点处激发的磁场强度dH z：沿单元环积分时，磁场dH′的方向不断改变，但是，沿z方向的投影不变，这样，dl的积分结果是总的磁场

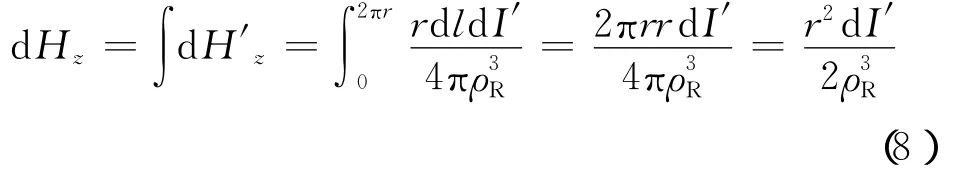
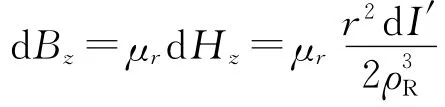
接收线圈内部通过的磁通量dΦ′为

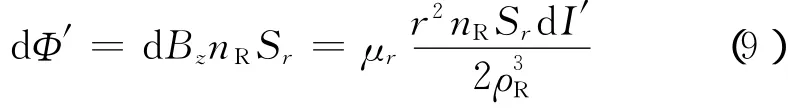
式中，Sr是接收线圈的面积；nR是接收线圈的圈数。这样电流环与接收线圈之间的互感

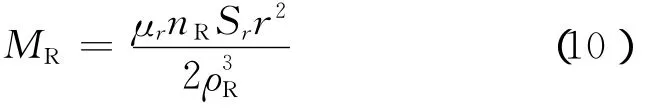
对磁通量dΦ′求导得到接收线圈中的二次感应电动势的微分

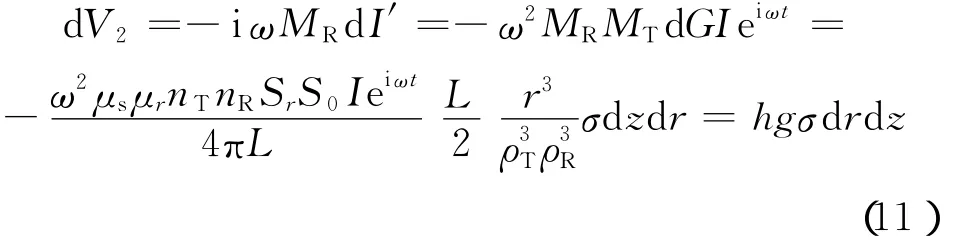
式中，h是与线圈有关的常数，描述2个互感响应；g是Doll几何因子。

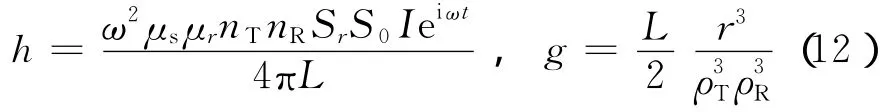
对式（11）在全空间中积分得到单个频率的二次场响应。

计算二次感应电动势时又对时间因子求了一次导数，表达式中又出现了一次频率ω，最终所得到的二次感应电动势与频率的平方成正比。

上述推导过程中，两次求导引出了两次频率因子，致使二次场的响应与频率的平方成正比。这一结论对瞬变电磁测井非常重要。另外，发射线圈产生的直接耦合一次场给出了所有位置的磁场强度，在单元环中该磁场强度产生磁感应强度，由此引出地层的磁导率；因为磁感应强度随时间变化，则在单元环中产生一次感应电动势，该感应电动势沿圆周方向构成回路，在单元环中产生感应电流，感应电流沿圆周方向流动，在空间产生二次磁场强度，该二次磁场强度在接收线圈内部产生磁感应强度，这时引出接收线圈内部的磁导率，该二次磁感应强度在接收线圈中产生二次感应电动势。接收线圈内部的磁导率对二次场响应影响比较大。二次场响应的频谱幅度与频率的平方成正比。

这是瞬变电磁测井对单个频率的二次场响应。瞬态激发的响应等于其频谱乘以对应频率的响应后叠加。方波或者阶跃的响应可以用这种方法得到：首先计算激发波形的频谱，然后计算每个对应频率的响应，将这些响应按照频谱叠加即得到其瞬态响应。

3 套管的影响

套管内部通常含铁，其磁导率大约是普通地层介质的1 000倍。相同的磁场，在套管中会激发出很强的电磁感应强度。套管的电导率大约是地层107倍，其感应电流是地层的1010倍，感应电动势也是地层的1010倍。所以，普通感应测井不能够在套管井中进行测量。

在套管井内，发射线圈产生的磁场强度H不因套管的存在而改变，套管内壁（井内）的液体中的电磁感应强度也不变；而在套管所占的空间中，因铁的存在，套管的电磁感应强度会发生剧烈变化，其强度是普通地层的1 000倍，这是因为套管的磁导率大。当电流环取到套管介质后，即电流环半径大于套管内半径、小于套管外半径时，在套管所占据的空间内，计算电磁感应强度时选取的磁导率应该是套管的磁导率；同样，计算感应电流时，也应该用套管的电导率，这时，其感应电动势是地层的1010倍。

Doll假设的电流环是独立的，电流环之间的相互作用没有考虑。在最终所得到的用几何因子计算响应的公式中，套管所占据的空间应该用套管的磁导率和电导率参数。套管是圆柱形状介质，可以用径向积分几何因子计算圆柱形状套管的响应。由于电导率和磁导率相乘以后是地层的1010倍，所以，在套管井的响应中，套管所产生的二次电磁场几乎占据或构成了其全部响应。

4 均匀无限大介质的响应

为了理解瞬变电磁测井原理，暂且不考虑套管的影响。选择2个激发电流时间不同的波形对无限均匀介质进行激发。图4所示是其激发波形。激发电流的持续时间为150 ms（红线）和300 ms（蓝线）。为了区分，绘图时将蓝线上移了0.05 V。将这2个波形作FFT得到图5所示的频谱，蓝线激发的频率低频成分幅度大，红线部分激发的频率成分低频幅度比较小，相应地高频成分比较多。

在反映地层的二次场的感应信号表达式式（8）中，线圈参数和线圈内部介质以及地层的磁导率参数固定以后，2个独立的等效互感是常数。对于均匀无限大地层，其几何因子积分以后为1，二次感应电动势的频谱与频率的平方成正比，与地层的电导率成正比。对于瞬变电磁测井，无限大均匀地层的二次感应测井响应V2的频谱为

图4 激发电流波形

图5 激发电流所对应的频谱

式中，K是常数。为研究无限大均匀介质中二次场的特征，取K为1。

从式（13）可以看出，瞬变电磁测井响应的一阶近似表达式中，其频谱与频率的平方成正比，比例系数包含地层的电导率参数。瞬变电磁响应的特征完全由式（13）确定。

通过改变激发波形延长时间研究其响应。将二次场的频率响应函数（13）与激发函数的频谱相乘以后得到图6所示的频谱。从图6中可以看到，随着频率的增加，高频成分的幅度值增加很多，总的趋势类似于直线上升。这是由于方波频谱总的变化趋势按照电流突变的频谱1／ω变化，与V2（ω）相乘以后，其频谱总的变化趋势与频率成正比。

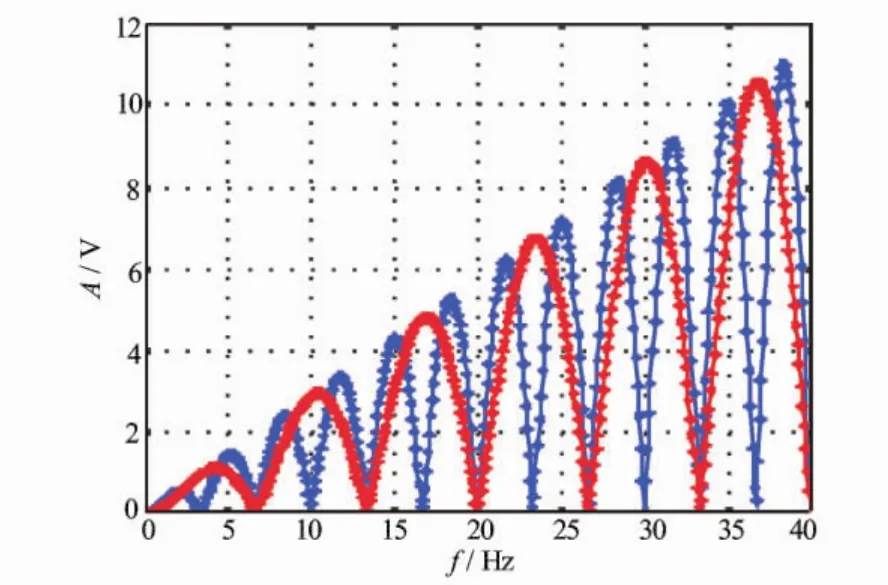
图6 激发频谱与二次场频谱相乘以后的频谱

这样的频谱将突出界面的影响。将上述频谱作FFT以后得到图7所示的响应。与图5所示的激发波形相比可以发现，在激发波形的突变处，地层的一次场响应有一个极大值；二次场响应有正、负2个脉冲，其脉冲的幅度与电导率成正比，电导率越大，其幅度越大。

在激发波形突变位置，di／dt极大，线圈中电磁感应强度最大，这个时刻地层的一次感应电动势也最大，其他时刻，由于没有激发波形突变，不会出现大的电磁感应现象，相应地也没有大的感应电动势。但是，由于地层的二次感应电磁场是对时间2次求导以后得到的，因此其响应曲线有正、负2个极值。从发射线圈到无限远，区域很大，不同区域的感应电动势对接收线圈响应的贡献幅度不一样，响应的时间有差别，因此，在最终的感应电动势响应中会出现一个过渡过程。

在所计算的响应中，开始位置有一个响应过程（见图8）。该过程刻画了二次场对瞬变激发波形的响应过程。从图8（a）上可以看出，2种不同激发波形的响应是完全重合的。为了区分这2个响应，将红线的响应加0.000 001进行绘图并得到图8（b）。该图刻画了二次场响应曲线的形状，描述了瞬变电磁测井响应的主要特征，它是阶跃激发波形的响应曲线，该形状不随激发波形中突变时间改变。

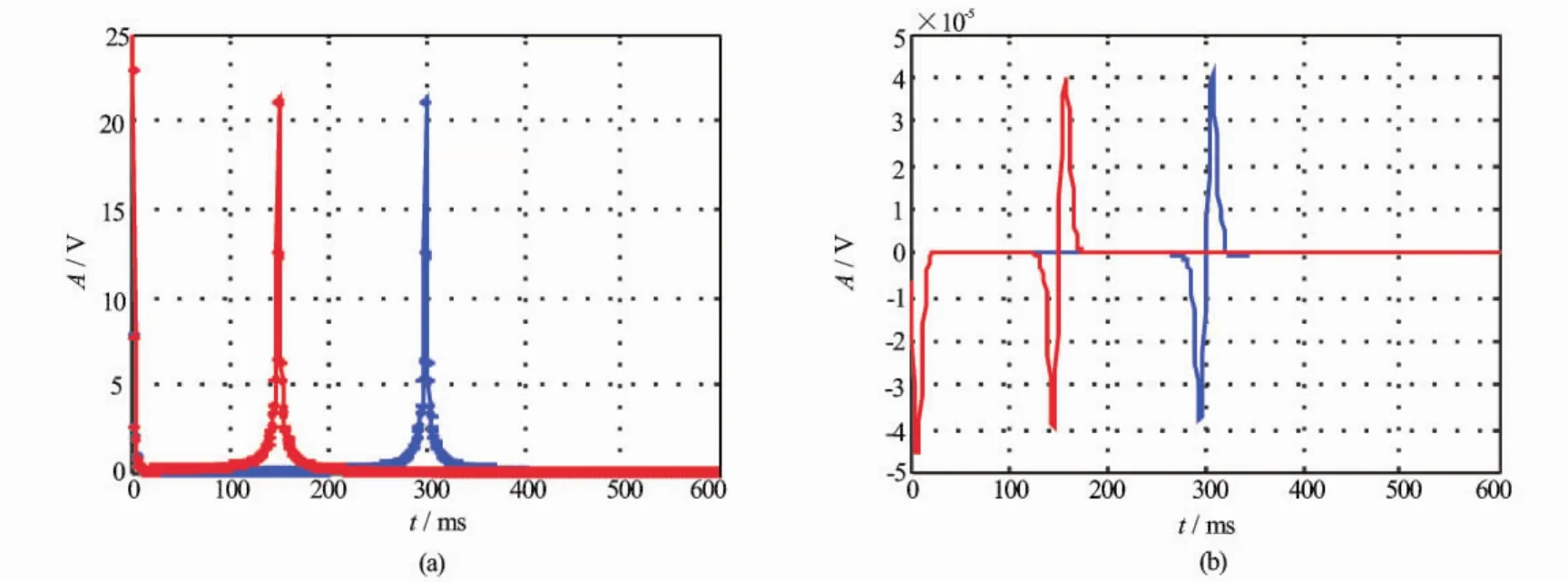
图7 2种激发波形的一次场（a）和二次场（b）响应曲线

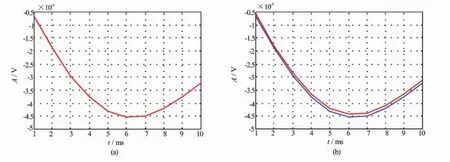
图8 起始时刻的二次场响应

从上述结果可以看出，用瞬变电磁场激发的二次场可以测量地层的电阻率，所测量的电阻率响应二次场只在激发波形突变的位置明显，其幅度与地层的电阻率成正比。可以用感应的Doll几何因子对其进行描述，建立不同深度的电阻率探测系统。

5 激发波形衰减形状的影响

瞬变电磁测井的二次场响应幅度与地层的电导率成正比，在用响应的幅度计算地层的电导率时，还必须研究其他因素对响应幅度的影响。因为实际的激发波形不可能像理论假设那样突变，总有一定的延迟。用一阶网络的指数响应对激发波形形状进行模拟，用指数函数e－pt代替突变。图9是指数函数过渡的波形形状及其对应的频谱（与阶跃函数的频谱绘制在一起进行对比），从图9（b）可以看到，由于激发波形的突变界面变化趋缓，低频成分增加［图9（b）的黑线和橙线分别是指数函数代替阶跃突变以后的频谱］。图10是电导率恒定，指数衰减系数p不同时所得到的二次场响应波形。从图10可以看到，激发波形的突变形状对二次场响应的影响比较大，p越小，其响应幅度越小。因为，此时突变不突出，电磁感应现象减弱，二次感应电动势减小。

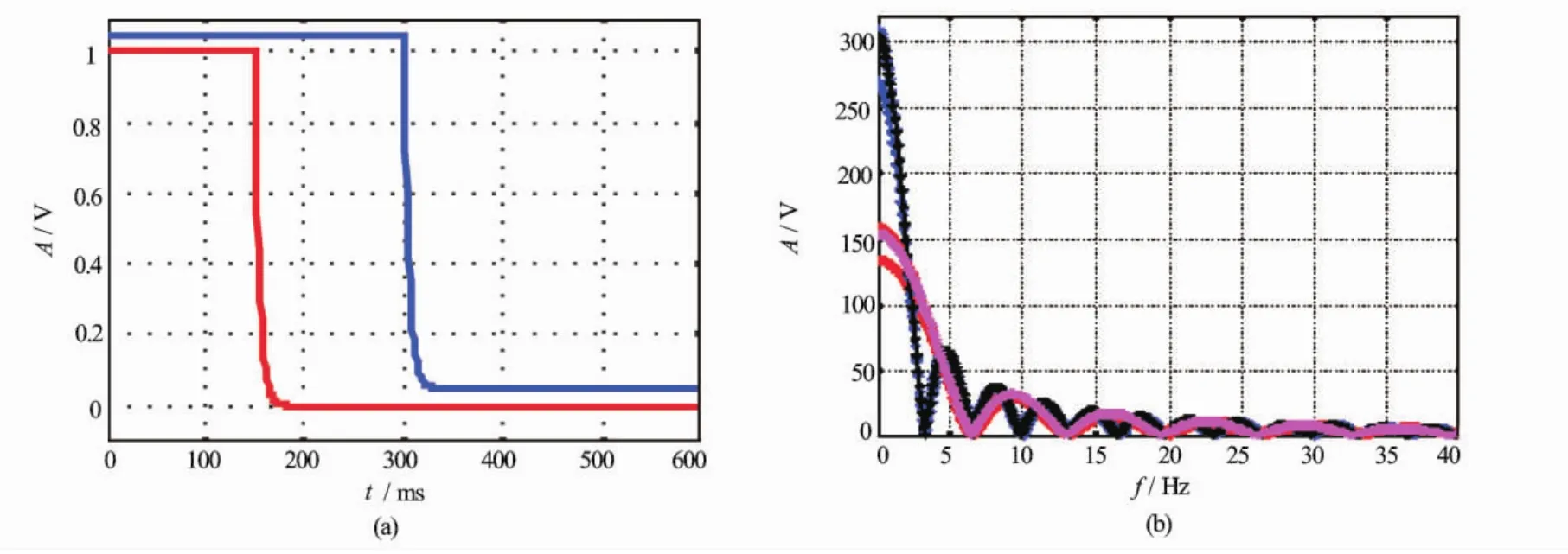
图9 改变电流突变的形状，用指数函数模拟突变时的波形及其对应的频谱（p＝0.2）

图10 激发电流变化形状对二次场感应电动势的影响

6 分析与讨论

为了更好地理解瞬变电磁测井测量二次感应电磁场的基本原理，按照Doll几何因子的推导过程，重点对所测量的二次电磁场的物理过程进行了推导。并用所得到的结果进一步计算了瞬变电磁测井对阶跃激励的二次场（一阶近似理论）响应。从响应中可以看出，在阶跃波形突变的位置，电磁感应最强烈，激发的一次场的感应电动势最大，二次感应电动势幅度在其两侧最大，瞬变电磁测井响应在阶跃位置出现近似正、负脉冲形状的响应，该响应曲线中包含了地层的电导率信息：电导率越大，整个响应曲线中二次场的幅度越大。或者说瞬变电磁测井携带地层电导率信息的方式是其曲线的幅度，在任意一个响应时间位置，其二次场响应的幅度都与地层的电导率成正比，只是时间不同，其幅度的大小有差别。

对于瞬变电磁激发源，阶跃激发源只是其中的一种理想源，还有一种理想激发源是脉冲，其频谱是所有频率的幅度都等于1。激发源的激发波形可以设计成各种形状，相应地，其瞬变电磁测井的响应也会出现各种丰富多彩的曲线形状。从这些所测量的曲线形状中对所测量地层的电导率进行反演，可以得到地层电导率随半径的分布。这是瞬变电磁测井的优势之一：通过改变激发源激发的波形形状设计出所需要的电磁测井仪器，完成需要的测量功能。

本文计算的响应是瞬变电磁测井中与地层电导率直接相关的部分，即二次场的响应。真正瞬变电磁测井所测量到的信号还包含一次场——直接耦合场。两者的叠加才是最终所记录到的测井响应。从Doll几何因子知道，直接耦合场与地层的电导率无关，与频率成正比，幅度比二次场大很多，刻画了系统的部分响应。与地层电导率有关的二次场由Doll几何因子给出（其一阶近似解），没有考虑单元环之间的相互作用，高频时受集肤效应影响比较大，低频时其幅度比较小。