路面不平度时域模型模拟方法研究

何 宁，石成英，周保顺

（1.第二炮兵工程大学，西安 710025； 2. 中国人民解放军96630部队，北京 102206）

路面不平度时域模型模拟方法研究

何 宁1，石成英1，周保顺2

（1.第二炮兵工程大学，西安 710025； 2. 中国人民解放军96630部队，北京 102206）

路面不平度是引起汽车系统振动的重要激励，路面不平度时域模型是研究公路运输平顺性的基础。本文根据国标GB/T 7031-2005中对路面不平的相关规定，研究讨论了路面不平度时域模型模拟常见的傅里叶逆变换法、谐波叠加法、滤波白噪声方法，对三种方法进行简单对比，并给出相应的实用范围。

路面不平度时域模型；傅里叶逆变换；谐波叠加；滤波白噪声

引言

当前，货物的公路运输在货运方式占中有重要地位，货物运输过程中的振动是不能忽视的现象，引起货物在车厢里振动的一个重要因素是路面不平度的影响[1]，对于路面不平度的时域模型的模拟是分析货物在车厢内振动的第一步。路面的时域激励的构建方法 有：傅里叶逆变换法、谐波叠加法、滤波白噪声、法蒙特卡洛法以及ARMA模型等方法[2]。本文比较详细地论述并讨论路面不平度模拟的傅里叶逆变换法、谐波叠加法、滤波白噪声三种常见方法，对三种方法进行简单对比，并给出相应的实用范围。

1 路面不平度的功率谱密度描述方式

在国标(GB 7031—2005)《机械振动 道路路面谱测量数据报告》中将路面不平度分为8个等级，并采用空间频率描述路面不平度的统计特性[3]。

式中：n是空间频率，n0参考空间频率，Gd(n0)是参考空间频率下的路面谱值，w是频率指数，确定每段功率谱斜线的斜率w=2。

路面不平度功率谱密度Gd(n)描述了路面高低起伏在长度方向上的统计特性，可把空间频谱函数Gd(n)转换为时间频谱函数Gd(f)。由功率谱密度函数定义，且f=vn，w=2πf，可得：

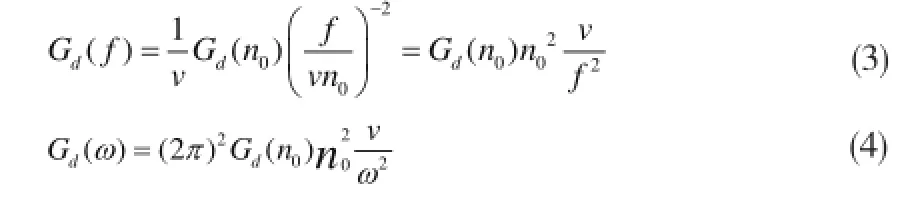
2 路面不平度时域模型模拟

2.1 傅里叶逆变换模拟方法[4]

路面不平度是平稳的、各态历经零均值的Gauss随机过程[1]。通过对路面不平度采样数据进行傅里叶变换可以求得路面不平度信号在频域范围内信息，所求解的频域信号包含的信息与原信号包含内容是一致的。如果通过构造频域内路面不平度采样信号，通过傅里叶逆变换就可求得路面不平度原信号。

由于车辆隔振系统作用，货物-车辆系统对某些频率激励响应极小，在进行路面不平度时域模型仿真时，可以忽略响应微小的频率段[4]，设频率范围为（fl,fu）。

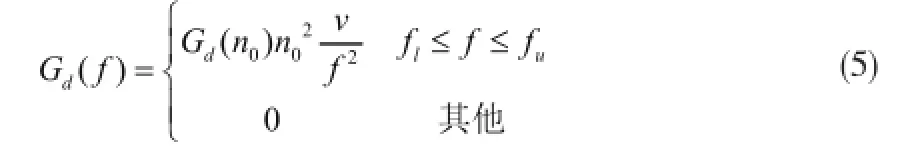
设Xm（m=0,1,…,N -1）是对路面不平度的采样数据，则其离散傅里叶变换为:

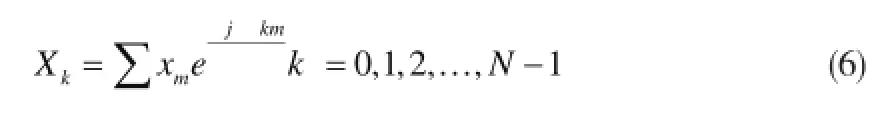
据离散傅里叶变换数据的特性，Xk(k=0,1,2,...,N-1)的实部关于N/2偶对称，虚部关于N/2奇对称[4]，只需要对Xk(k=0,1,2,...,N/2)进行离散，对Xk的后N/2个离散傅里叶变换值进行补齐，就可得到Xk(k=0,1,2,...,N-1)。

根据文献3可得出Xk的幅值与路面不平度的功率谱密度Gx(fk)的关系为:

式中:fk=fl+kΔ f。

设随机数Xk的相角为φk，则有:

φk是（0,2π）间随机数。

对Xk(k=0,1,2,...,N-1)进行离散傅里叶逆变换得到路面不平度空间模型。

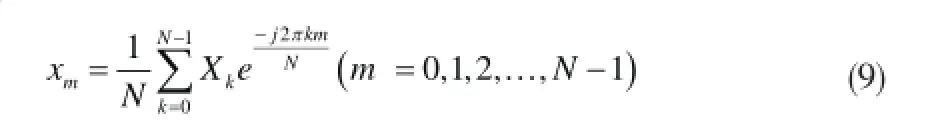
2.2 谐波叠加模拟方法[5]

谐波叠加法是采用离散谱逼近目标随机过程的方法，随机信号通过离散傅里叶变换为一系列随机相位的不同频率和幅值的正弦波，将大量具有随机相位的正弦或余弦波加和就能模拟路面不平度。

根据国标[3]中对功率谱密度函数的定义。

将模拟频率区间（fl,fu）划分成等长度的m个小区间，对于第i个小区间，采用中心频率fmid_i整个小区间内的频率值，采用其中心频率fmid_i处的功率谱密度来代替整个小区间上的功率谱密度的值，就能得到第i个小区间的功率谱函数。

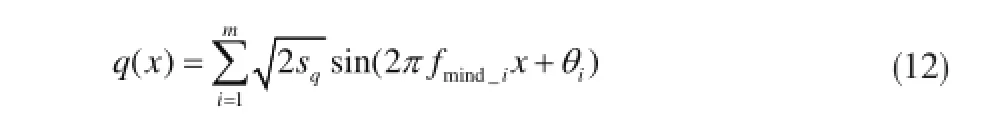
将路面不平度的空间域模型转换为时域模型，将x=vt代入式，即可得时域随机路面不平度输入。

式中，θi为在（0，2π）上均匀分布的随机相位角。

2.3 滤波白噪声模拟方法[6]

滤波白噪声法计算相对稳定，将路面不平度看作是白噪声激励的一阶线性系统的响应。

当ω→0时，Gd(ω)→∞，所以式(4)的功率谱密度可以改写为：

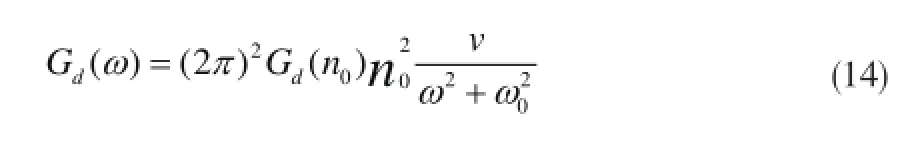
式中，ω0为最低截止角频率。

由线性系统输出对输入激励在频域内的响应规律：

式(15)、(16)中：q(ω)为路面不平度频域信号，H(ω)为频响函数，Sw=1为白噪声w(t)的功率谱密度。

由和可得频响函数：

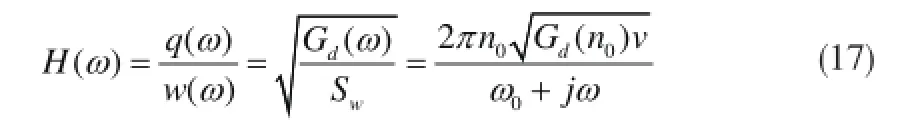
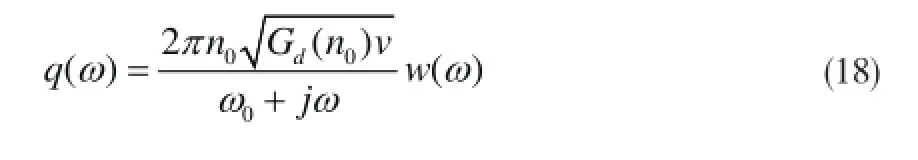
式经拉氏逆变换，可得到路面不平时域度的一阶微分方程：

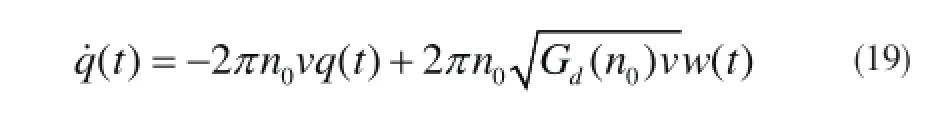
式中，q(t)为路面不平度的时域信号，w(t)为数学期望为零的高斯白噪声信号，v为车辆速度。

3 结论

傅里叶逆变换法采用基于功率谱密度的离散数据采样，能够简单、精确重构道路的时域模型，该方法可用于任意指定谱特征的随机过程的模拟，具有普适性，为方便使用傅里叶逆变换，常使 用Matlab编程实现。谐波叠加法数学意义明确，适用于任意指定的谱特征，但是模拟过程中包括大量的三角函数运算，要得到精确的合符谱值的模型，则离散度要细，容易使计算量十分大，但容易采用一般编程语言实现，在许多需要路面不平度作为输入的仿真分析中，常采用谐波叠加法生成路面不平度的时域序列，所以有广泛的使用范围。滤波白噪声法计算量相对谐波叠加法要小、速度较快，但是其模拟精度较差，在对设备振动信号提取时需要有针对性设计滤波器，常运用在Simulink仿真中。

[1] 陆兆峰. 车辆对路面作用的力学行为研究[D].西安:长安大学, 2005. 5.

[2] 夏俊忠,马宗,白云川等. 路面不平度激励模型研究现状[J].噪声与振动控制, 2012.10.

[3] GB/T 7031-2005 机械振动道路路面谱测量数据报告[S].

[4] 徐海亮. 车辆-道路耦合系统随机振动研究[D].上海：同济大学土木工程学院, 2008.10.

[5] 路永婕. 重载汽车与路面相互作用动力学研究[D].北京：北京交通大学, 2010.10.

[6] 张永林. 车辆道路数值模拟与仿真研究[D].武汉：华中科技大学, 2010.10.

何宁（1988-），籍贯：四川广安，硕士研究生，主要从事装备运输安全性与可靠性分析。

Research on the Method to Simulate the Time-domain Road Roughness

HE Ning1, SHI Cheng-ying1, ZHOU Bao-shun2
（1. The Second Artillery Engineering University, Xi’an 710025; 2. 96630 Troops of People's Liberation Army, Beijing 102206）

Road roughness is one of the most impor tant excitation to arise the vibration of a vehicle system. The time-domain model of road roughness is the basis of research in road comfort. In this paper, according to the provision of National standard GB/T7031-2005 about road roughness, the common methods are discussed in detail to simulate time-domain model of road roughness, including Fourier inversetrans form method, partial wave adding method, and filtered white noise method. Finally, simple comparison of them and relevant application field are listed.

time-domain model of road roughness; Fourier inverset ransform; partial wave adding; filtered white noise

U461.5+6

B

1004-7204（2014）03-0050-03