冲击台冲击波形的确定方法

王延停，税 利，张 旭

（中国洛阳电子装备试验中心，洛阳 454750）

环境试验设备

冲击台冲击波形的确定方法

王延停，税 利，张 旭

（中国洛阳电子装备试验中心，洛阳 454750）

本文对冲击台在冲击试验前，因测试冲击波形是否符合试验要求而所做的过多模拟测试，会导致试验效率较低、试验材料浪费等问题，在数据试验的基础上，运用泰勒公式和最小二乘法，将复杂的物理模型转化为若干个简单的数学模型，给出了一种冲击台的波形发生器的模拟选定和冲击台提升高度的确定方法，以确定冲击波形。测试数据表明，该方法建立的冲击波形的确定方法是可靠的。

冲击波形；泰勒公式；最小二乘法；数据模拟

引言

SY11-50冲击台是全自动气压提升冲击测试系统，用于测量和确定产品或包装的抗冲击性能，考核试品在冲击环境下功能的可靠性和结构完好性。由于在冲击试验前，试验员无法确定冲击台所完成的冲击波形是否符合试验要求，所以在正式的冲击试验前需使用质量相近的模拟试品（配重块）先做模拟冲击试验。但过多的模拟测试不仅浪费试验时间和试验材料，而且对冲击台的使用寿命也会产生影响。因此本文致力于寻找一种电脑的模拟方法，代替试验中的模拟测试。

由于冲击波形与试品重量、冲击台提升高度、波形发生器的硬度和厚度等因素有关，所以建立模型时需要考虑波形发生器的密度、屈服力、杨氏模量、泊松比、试品重量以及冲击台提升高度等参数，因此所建立的模型的函数关系式将十分复杂。

在实际工作中，测量和计算数据时常常要求用比较简单的计算方法得到一定精度的计算结果，这就是近似计算问题[1]。不论在近似计算或理论分析中，我们希望用一个简单的函数近似表示一个比较复杂的函数，这将带来很大的方便。一般说来，最简单的是多项式[1]。因为任何连续函数都可以泰勒展开，通过取展开前的前几项构成泰勒展开[2-5]，因此本文运用泰勒展开将复杂的物理模型转化为简单的数学多项式，并在数据试验的基础上，利用最小二乘法，求得了多项式的系数值。从而给出了一种冲击台波形发生器的模拟选定和冲击台提升高度的确定方法，以确定冲击波形。

1 波形发生器的选定和冲击台提升高度的确定

1.1 函数模型的建立

考虑试品在试验前，被试方需给出确定的峰值加速度和脉冲宽度以确定冲击波形。因试验时决定峰值加速度和脉冲宽度的因素是试品重量、冲击台提升高度、波形发生器的选定，因此在选定一种波形发生器后，峰值加速度、脉冲宽度、试品重量、冲击台提升高度将存在一种函数关系。

不妨设峰值加速度为G，脉冲宽度为K，试品重量为M，冲击台提升高度为H，虽然我们不知道它们具体的函数关系式，但利用泰勒展开它们将有一种近似的函数关系式，即

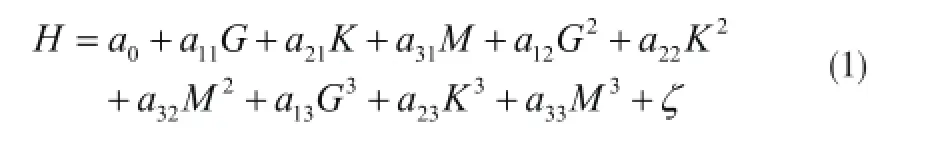
其中，

(a0, a11,a21,a31,a12,a22,a32,a13,a23,a33)为系数，ζ→0。

而现在我们的问题转化到如何求系数：(a0, a11,a21,a31,a12,a22,a32,a13,a23,a33)。

如果我们做n(n≥10)组模拟试验，就能得出n组(H, G, K, M)的值，由(2.1)则有

则有

这是一个线性模型，应用最小二乘法可得，系数的解β=(XTX)-1XTY[6]。事实上，如果系数确定后，给定G、K、M，我们可以求出H的大小。这时，我们可以确定一种波形发生器的函数关系。

同理，我们可以确定多种波形发生器的函数关系。因为波形发生器的种类有限，所以现在我们将复杂的物理模型转化为了若干个简单的数学模型。

1.2 波形发生器的函数模型的系数的正确性验证

各种波形发生器的函数模型的系数确立之后，需要验证其正确性。为验证本文所建立的函数模型的正确性，我们取红色一号波形发生器的函数模型进行实验验证，试验中共获取了52组数据。根据公式(1)，我们将数据代入，并利用最小二乘法计算，得到系数β的值，将系数β代入公式(3)求得H的估计值的大小，将其与H的实际值的大小比较，则可看出二者的拟合情况。图1为红色一号波形发生器提升高度H的实际值与估计值的拟合对照图。其中，横坐标表示数据序列，即在不同重量M下，所进行的实验次数；纵坐标表示冲击台的提升高度H；data1“*”号表示H的估计值，data2“.”号表示H的真实值。

从图1可以看出，红色一号波形发生器的提升高度H的估计值与真实值的拟合的很好，证明该种波形发生器的函数模型的系数是正确的。同理，可以验证其它的波形发生器的函数模型的系数是正确的。

1.3 波形发生器的选定和冲击台提升高度的确定

因为SY11-50冲击台提升高度有限（0≤H≤0.5m ），所以根据每种波形发生器所求的H的大小，我们就能知道哪种的波形发生器合适。

在实际应用中，首先计算得到每种波形发生器对应的距离H的大小，然后比较哪种波形发生器是我们所需要的，如果一种波形发生器对应的距离H，在冲击台提升高度限度之内，就认为该种波形发生器是我们所需要的。但如果有多种波形发生器符合要求，哪一个才是最适合的？为此，需要给出一个客观而明确的基准值作为判断标准。

图1 红色一号波形发生器的拟合对照图

很明显，一种波形发生器对应的距离H越处于冲击台提升高度中间，它合适的概率就越大的，将这种概率记为y，因此y服从于正态分布。由于0≤H≤0.5m，所以E( H)=0.25m，根据中心极限定理，我们知道y·N(0.25,σ2)，因σ2的具体值相对来说不重要，不妨设为1，则有

根据每种波形发生器所对应y的大小，我们就可以得到了波形发生器的选定方法。波形发生器选定后，根据公式(1)，我们可以得到冲击台提升高度的确定方法。

1.4 冲击试验波形发生器的选定方法的可靠性测试

冲击试验波形发生器的选定方法建立之后，需要对其可靠性进行测试，通过测试数据论证模型的可靠性。为进行测试本文随机选取了9组数据进行测试，测试结果见表1，其中试品重量M的单位是kg，提升高度H的单位是m，加速度G的单位是1× 100m2，脉冲宽度K的单位是1× 10ms。

给定随机选取的9组数据后，根据冲击试验波形发生器的选定方法可以选定最优的波形发生器及确定相应的提升高度，此时进行冲击试验可以得出9组数据分别对应的脉冲宽度和加速度。从表1可以看出，脉冲宽度的误差率和加速度的误差率均不超过冲击实验所要求的10%的误差率，因此冲击试验波形发生器的选定方法是可靠的。

2 结论

1）本文在数据试验的基础上，运用泰勒展开和最小二乘法，将复杂的物理模型转化为若干个简单的数学模型，给出了一种冲击台波形发生器的模拟选定和冲击台提升高度的确定方法，以确定冲击波形。

表1 冲击试验波形发生器的选定方法的可靠性测试结果

2）将复杂的物理函数模型转化为若干个简单的数学函数模型，然后应用泰勒展开，有利于把复杂问题简单化，一定的的理论价值。

3）本文的进行的可靠性测试证明了本文方法的正确性，因此本文方法可直接应用于冲击试验，具有应用价值。

[1] 陈传璋,金福临,朱学炎,欧阳光中.数学分析[M].北京:高等教育出版社,2005.

[2] 王正林,龚纯,何倩.精通MATLAB科学计算[M].北京:电子工业, 2008.

[3] 秦国强.多元函数的泰勒公式及其应用[J].吕梁教育学院学报,2013,30(2).

[4] 刑永丽,陈建春.泰勒级数在近似计算中的应用[J].湘潭师范学院学报（自然科学版）,2004,26(1).

[5] 陆健.最小二乘法及其应用[J].应用数学,2008.

[6] 王松桂.线性模型的理论及其应用[M].合肥:安徽教育出版社,1987.

Method for Determining Impulse Waveform From Shock Machine

WANG Yan-ting, SHUI Li, ZHANG Xu
（Luoyang Electronic Equipment Test Center of China, Luoyang 454750）

The problems which due to test whether the shock waveform conform the requirements of the impact test exist in the test efficiency slowly and the waste materials. On the basis of experimental data, this project using Taylor formula and the least square method put the complex physical model into several simple mathematical models. A shock waveform generator simulation selected and impact machine height determination method is given out to determine the shock wave. Examples show that the function model is correct.

impulse waveform; Taylor formula; least square method; digital simulation

TH136

B

1004-7204（2014）03-0052-03

王延停（1986-），男（汉族），山东聊城人，硕士，主要从事环境试验和数据处理。

税利（1983-），男（汉族），四川乐山人，硕士，主要从事环境试验和导航对抗。

张旭（1983-），男（汉族），河南商丘人，本科，主要从事数据处理和质量管理。