液压振动台功率谱复现控制研究

王一飞，陈 宇，陈章位，栾强利

（1.中国船舶重工集团公司第七二三研究所，扬州 225001；2.浙江大学流体动力与机电系统国家重点实验室，杭州 310027）

技术专栏

液压振动台功率谱复现控制研究

王一飞1，陈 宇2，陈章位2，栾强利2

（1.中国船舶重工集团公司第七二三研究所，扬州 225001；2.浙江大学流体动力与机电系统国家重点实验室，杭州 310027）

PID控制因为结构简单、稳定性好、可靠性高等优点被广泛应用。针对实际控制系统往往存在非线性因素，常规PID不能满足实际需求，设计了基H1法频响函数估计的变参数PID控制算法。通过对两点激励液压振动试验系统进行随机振动试验，表明H1法变参数PID控制算法对振动台具有良好的控制效果，可以实现高精度的功率谱复现。

液压振动台；H1估计；变参数PID控制；功率谱复现

引言

液压振动台具有大位移、大推力、低频响等特点，因此被广泛的应用于振动环境模拟试验中，通过振动环境模拟，可以对试件进行振动工作环境的模拟，从而提前发现产品设计过程中存在的缺陷，并进行改进，以保证产品工作的稳定性和可靠性。目前，液压振动台作为振动环境模拟试验的一种重要试验设备，普遍应用于航空航天、兵器制造、船舶制造以及核工业建设等重要的国防工业领域和汽车制造、建筑施工、道路修建等众多民用工业。

液压振动台是在电液伺服技术的推动下迅速发展起来的，伺服控制技术能够实现对液压振动台的基本运动控制，并能够保证液压振动台具有足够频宽及其工作稳定性。考虑实际控制系统往往存在非线性因素，常规PID不能满足实际需求，研究了电液振动试验系统变参数PID控制技术的实现方法，设计了基于H1频响函数估计变参数PID控制算法，并通过振动试验进一步验证了控制可靠性和稳定性。

1 H1频响函数估计法系统辨识

功率谱复现试验振动控制过程为先辨识被控系统的频响函数，计算系统阻抗；然后依据系统阻抗生成驱动信号激励系统，测量响应功率谱并计算控制误差谱；之后对驱动信号进行修正，使信号的输出满足控制精度要求。频响函数估计是振动控制过程的基础，其估计结果直接关系振动控制的精度。

在实际系统中，输入和输出端均存在噪声，系统模型如图1所示，其数学模型可以描述为:

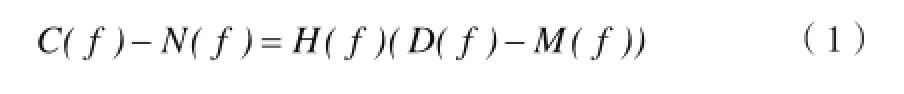
其中，H(f)是待估计系统的频响函数，D(f)和C(f)别是输入输出信号谱,M(f)和N(f)分别是输入输出端噪声谱。

H1估计法所用的模型假设输入信号测量不存在噪声，且输出测量噪声N(f)与输入信号D(f)互不相关，则H1 估计法所得频响函数的估计结果为

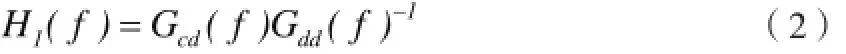
式中，H1(f)为使用H1估计法所得的频响函数估计结果，为输出测量与输入测量的互功率谱均值，为输入测量的自功率谱均值。

H1(f)与系统真实频响函数H(f)的关系为:

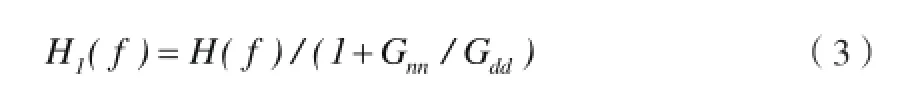
式中，Gnn(f)为输入噪声的自功率谱均值。

由上式可知H1估计法虽不能消除输入噪声的影响且是欠估计，但对于瞬间波形复现试验，由于H1估计模型较简单准确，试验时间较短，复现精度高等优势，故采用H1法频响函数估计。

2 变参数PID控制算法

根据线性振动理论可知：

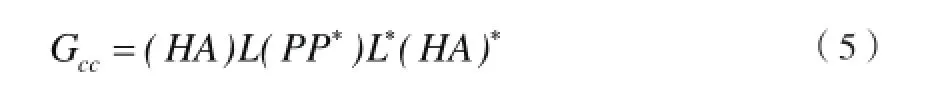
R为参考谱，H*为频响函数的共轭函数，L是对角元素为实数的下三角复数矩阵，P是时域随机化过程随机相位矩阵，A是补偿矩阵。

理想情况下测量得到的补偿矩阵与系统的频响函数矩阵的乘积应该是单位矩阵，即：

但是由于系统的非线性振动、随机信号生成过程中的泄漏、功率谱估计误差等原因，频响函数H和补偿矩阵A的乘积不是单位矩I，而是近似等于单位矩阵的Ĩ，即：

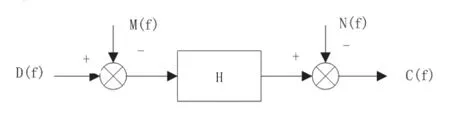
图1 多输入多输出系统模型

式（7）代入式（5）得:

引入修正矩阵Λ，满足：

在不考虑互谱控制的条件下，Gcc、R、L、Λ都是对角矩阵。整理式（9）得：

定义：

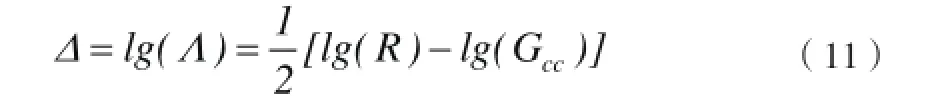
引入PID修正：

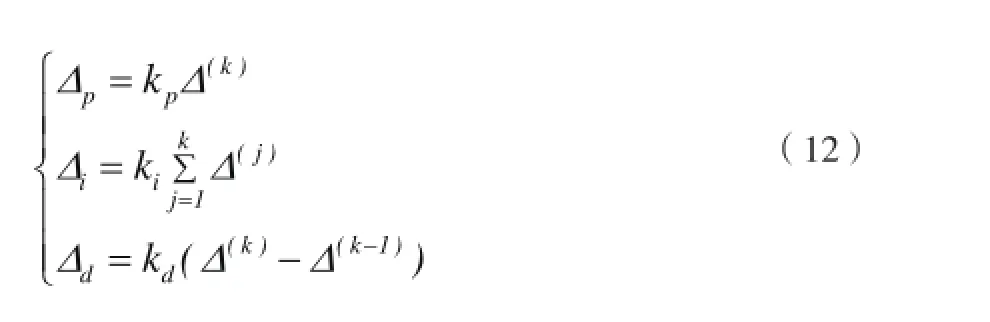
修正量U定义如下：

整理可得修正量U：

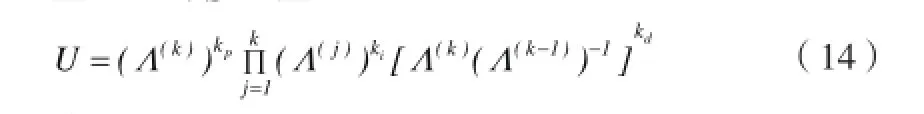
修正L：

其中式（10），（11），（12）为PID控制算法。

kikpkpki由控制理论可知：当kp值较大时，修正速度加快，但同时振荡次数加多，影响修正的精度；当kp值较小时，修正速度缓慢。功率谱和参考谱之间的误差较大时，kp的值宜大些，误差较小时，kp的值宜小些。当ki值较大时，系统振荡次数增多，但能消除稳态误差。当功率谱和参考谱之间误差较小时，宜采用值小ki降低功率谱的大幅度的波动。引入kd加快修正的速度，减小超调，但值过大时，其影响相反。在误差较大时，可适当增大kd，但是考虑到功率谱估计的随机误差的影响，三个参数不宜很大。PID参数设定如下：

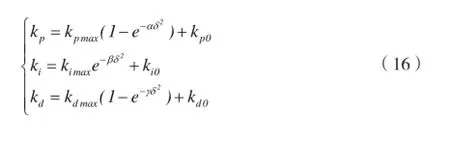
式中、α、β及γ是待定系数，kpmax,kimax,kdmax是变化幅度且属于区间（0，1），kp0,ki0,kd0是各参数的初值且kp0≤1-kpmax。

由框图2可得变参数 PID 控制算法闭环传递函数：

求解极点可知：kd＝0时，Gpid（s）只有一个极点，且为幅值；当kd≠0时，Gpid（s）有两个极点，这两个极点均在复平面的左半面时，变参数PID控制算法就收敛。

基于H1法频响函数估计变参数PID控制的功率谱复现算法如图3所示：利用系统阻抗和参考信号与控制信号偏差的频谱对驱动信号谱进行修正，以使控制波形能够高精度地复现参考波形。

3 随机试验

基于H1法频响函数估计变参数PID控制算法对液压振动台进行试验控制研究，试验对象选用浙江大学流体动力与机电系统国家重点实验室两点激励液压振动试验系统（图4），对算法控制效果进行试验验证，振动台参数如表1所示。

图2 变参数PID控制算法框图

图3 功率谱复现过程

液压振动台功率谱复现试验如图5所示，目标有效值为0.1g，整个功率谱密度范围为5～100Hz。其中（a）为控制点1试验结果，（b）为控制点2试验结果。控制试验中，2个通道的响应谱与参考谱的偏差均控制在±3dB容差内，表明基于H1估计变参数PID控制算法能够实现液压振动台高精度的功率谱复现。

4 总结

PID控制的设计思想是依靠过程误差来消除误差，不必完全依靠系统的数学模型。本文根据系统实际情况，提出了一种简单、易实现的基于H1估计变参数PID 控制方法，H1法考虑系统输出端的噪声同时具有收敛速度快，低频响应精度高的优点。通过对两点激励液压振动试验系统进行随机振动试验表明：基于H1估计变参数PID控制算法对振动台系统具有很好的控制能力，能够高精度实现功率谱波形复现。

图4 液压振动台

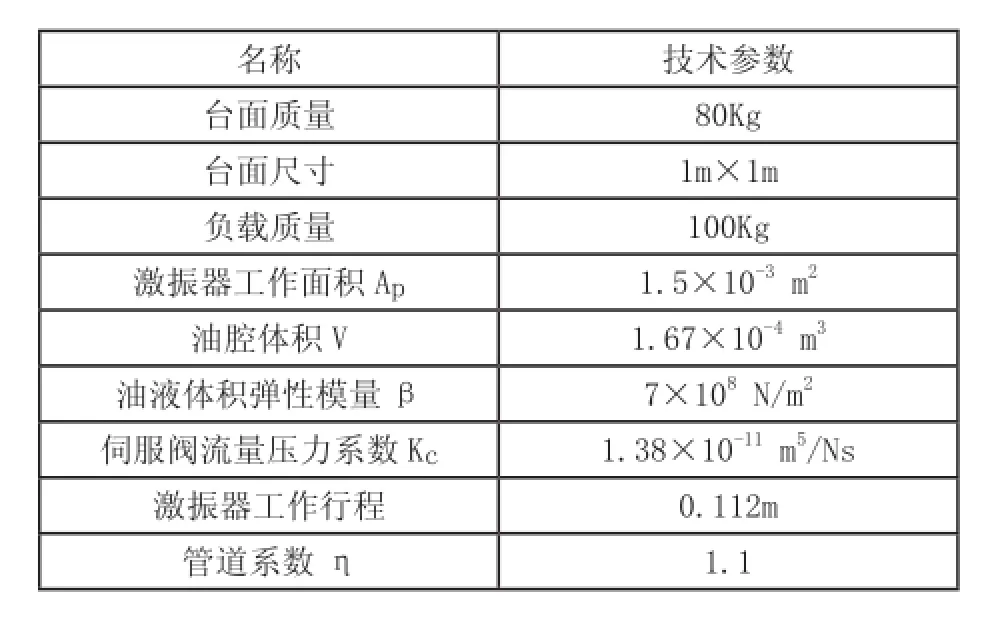
表1 液压振动台参数

图5 液压振动台功率谱复现试验

[1] 王燕华, 程文瀼. 地震模拟振动台运动控制性能分析[J].振动与冲击, 2012, 29(2): 99-106.

[2] 韩俊伟, 李玉亭, 胡宝生. 大型三向六白由度地震模拟振动台[J].地震学报,1998, 20(3): 327-331.

[3] Shortreed J S, Seible F, Benzoni G. Simulation issues with arealtime, full-scale seismic testing system [J]. Journal of Earthquake Engineering, 2002, 6(Sp. Iss. S1): 185-201.

[4] 钟庆昌,谢剑英,李辉.变参数PID控制器[J].信息与控制, 2008, 28（4）: 1-3.

Research on the Control of Power Spectrum Density Replication

WANG Yi-fei1, CHEN Yu2, CHEN Zhang-wei2, LUAN Qiang-li2
（1.The 723th Research Insti tute, China Shipbuilding Industry Corporation, Yangzhou 225001; 2. The State Key Lab of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027）

PID cont rol strategy with high stability and high reliability is widely used for its simple structure. Conventional PID can’t meet actual demand when the nonlinear factors exit in the control system, then a variable parameter PID control algorithm based on H1 est imator is proposed. A random vibration test is conducted on a two-exciter testing system, and the results show that this algor ithm has good effect on the system and can realize high precision power spectrum density (PSD) replication.

hydraulic shaker; H1 estimation; variable parameter PID control; PSD replication

TH137

A

1004-7204（2014）03-0046-04

王一飞（1971-），男，江苏扬州人，工程师，主要从事电工电子产品的环境适应性研究。