用De l t a法求两水平研究中信度的置信区间

陈彦垒 叶宝娟

一、问题提出

在教育、心理、管理等科学领域中，很多研究现象的数据结构都体现为两水平（两层）的数据结构，如学生嵌套在班级中、员工嵌套在企业中，在此，学生、员工代表了数据结构的第一层，而班级、企业代表了数据结构的第二层。近年来，越来越多的研究者采用两水平研究，以便更准确地研究变量间的关系。在两水平研究中，被试嵌套于更高的单元中，在研究现象上相关，即在所用的测验量表或题目上被试不独立，单元内的被试相互关联。举例来说，有研究表明，任务绩效风险考量、组织利益风险考量、领导成员交换、组织集权度会影响管理者的授权行为，不同企业的任务绩效风险考量、组织利益风险考量、领导成员交换、组织集权度不同，因此，不同企业的员工在评价管理者的授权行为时，就会有不同的表现。这样，在研究任务绩效风险考量、组织利益风险考量、领导成员交换、组织集权度对管理者授权行为的影响时，我们可以采用两水平研究：员工嵌套在企业中，同一企业员工在作答《管理者授权行为》量表时，作答情况会类似、相互关联，不同企业员工在作答《管理者授权行为》量表时，其作答情况差别很大、没有关联。[1]

在两水平研究中，我们经常会提到信度λj和λ。[2][3]信度λj和λ用于衡量两水平研究中参数估计的精确性。研究者在重视λj和λ点估计的同时，应重视其区间估计，通过区间估计，我们可以了解信度估计的误差，从而更准确地对其进行评价。[4][5]Delta法近年来被广泛应用于求解信度的置信区间。本文首先介绍了λj和λ的含义及其基于的模型，在此基础上，提出了简单而精确地估计λj和λ置信区间的新方法。实例表明，相对于Raykov等人介绍的方法，新方法操作起来更简单，得出的结果也更精确。

二、λj和λ的含义及其基于的模型

信度λj和λ指的是参数统计估计的信度或精确性。λj是第j个单元样本均值的信度，表示第二水平第j单元的“真实”变异（或真正的单元的变异）占第一水平上观测到的参数估计的变异的比例；[6]λ经常被称为平均信度、均值的总体信度或总体均值信度（overall mean reliability），表示第二水平单元的平均值在各个第二水平单元间的变异中真参数（相对于估计误差方差）所占的方差比例，λ的值越小，表示单元间的变异越小。[7][8]

在两水平研究中，Yij表示第二水平第j（j=1，...，J）个单元的第i（i=1，...，nj）个被试的观测分数，两水平研究所基于的阶层模型，可由如下两个方程来定义：

阶层一水平的方程：

阶层二水平的方程：

其中，γij是Yij对第j个单元的均值 β0j的偏差，γij是正态分布，均值为0，方差为 σ2；u0j是第j个单元的均值对总均值γ00的偏差，与γij不相关，均值为0，方差为τ00。我们将公式（2）代入公式（1），可得：

ρj表示第二层第j个单元的真分数的方差与观测分数方差的比率。[9]公式（4）的信度系数只是第j个单元的信度系数。在此基础上，研究者提出了一个更一般的信度，表示基于单元均值的信度的总体测量，定义为所有特定单元信度系数的均值，公式如下：

ρ系数经常被称为均值的总体信度（或总体均值信度）。ρ系数越高，样本单元均值作为第二层水平的均值，真值的指标就越可靠。如果在第二水平上添加其他预测变量，方程（2）变为会发在两水平研究中，如果多层线性模型的变量发生变化（增加或减少变量），如公式（7）所示，λj和λ的值可能发生变化。

三、估计λj和λ置信区间

公式（4）、（5）、（8）、（9）仅是 λj和 λ 点估计，而点估计提供的信息量有限，不能给出估计的偏差，用λj和λ的区间估计可以帮助应用工作者对两水平研究中参数估计的精确性作出更准确的评价。[10]Delta法近年来被研究者广泛用于求信度的置信区间。[11][12]叶宝娟和温忠麟的研究显示，Delta法是一种求参数置信区间的比较好的方法，这种方法简单而精确。[13]

2010年，Raykov等人采用Delta法求ρ的标准误，如公式（6）所示：

Raykov等人采用Delta法求ρ的标准误后，为了保证求得的ρ的范围是0＜ρ＜1，又引进了额外参数κ，并在κ和ρ之间建立了下列关系：

其中，ln（.）表示自然对数。用Delta法求κ的标准误：

则κ的100（1-α）%的置信区间为：

研究者求得κ的置信区间后，即可求出ρ的置信区间：

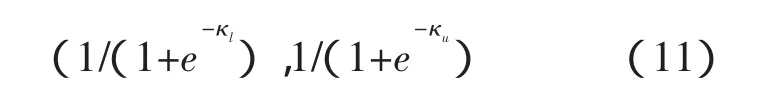
其中，κl，κu分别表示κ的置信区间的下限和上限。

总结起来，采用这种方法求ρ的置信区间有两个不足：

（1）比较麻烦。Raykov等人的研究给出了用R软件完成这个计算过程一系列的变换，最后求得ρ的置信区间，这个过程比较麻烦。虽然R软件的计算程序是现成的，但不熟悉R软件的应用工作者（一般的应用工作者较少用R软件）完成这个计算过程并不容易。

（2）不精确。Raykov等人的研究中，求ρ的置信区间的过程有两个近似过程：用Delta法求ρ的SE的过程是近似过程；引进了额外参数κ，用Delta法求κ的SE时又进行了一次近似计算，此过程用到ρ的SE，相当于进行了两次近似计算，此时求得的κ的置信区间的上限和下限是两次近似计算后得到的，进而用κ求ρ的置信区间，相当于求ρ的置信区间的过程进行了两次近似计算。

四、估计λj和λ置信区间方法的改进

Raykov等人的研究中，求得ρ的SE后，引进额外参数κ求ρ的置信区间的方法并没有改变ρ会大于1或小于0的事实，只是换了一种方法，使ρ在0和1之间。实际上，达到此目的远不用这么麻烦，换用一种比较简单的方法就可以，即先用Delta法求出ρ的SE，进而直接用下式求得ρ的置信区间：

如果求得的ρ的置信区间的范围已经在0和1之间，那么ρ的置信区间就为实际求得的置信区间，这比Raykov等人提到“还要经过一次转化再求得的置信区间”的方法要相对精确。如果求得的ρ的置信区间的下限小于0，上限大于1，研究者只需舍弃此范围外的数值，即如果下限小于0，将小于0的部分舍弃，下限取到0，此时求得的上限至少是相对精确的；如果上限大于1，将大于1的部分舍弃，上限取到1，此时求得的置信区间的下限是相对精确的。如果求得的ρ的置信区间的下限小于0，上限大于1，此时求得的置信区间为（0,1），只有此种特殊情况下得出的结论，与采用Raykov等人介绍的方法得出的结论一致，精确程度较低。

用本文介绍的新方法求ρ的置信区间，只需在Mplus程序中“OUTPUT”中添加一个“CINTERVAL”命令，此时用结构方程软件Mplus求得所需要的信度的点估计值，用Delta法计算得到的标准误，用Delta法计算得到的信度的95%和99%的置信区间，并且Mplus程序会自动将上限大于1，下限小于0的数值舍弃，程序给出的最大上限为1，最小下限为0，读者直接报告程序给出的置信区间即可。如果程序给出的置信区间的上限为1，下限为0，读者报告置信区间时不取到0或1即可，这种方法非常简单，也非常容易理解。

五、用D e l t a法求阶层线性研究中测验信度的置信区间示例

某学业能力测验施测于600名被试，这600名被试来自12所学校，估计这个测验的单元均值信度、总均值信度及其置信区间。用Mplus6.11软件求12所学校的单元均值信度和总均值信度的点估计值、标准误，以及本文介绍的新方法求信度置信区间的计算程序如下：

这个程序与普通的两水平模型程序差不多，不同的是增加了几个额外参数。由于这个模型是饱和模型（saturated model），模型拟合完美（perfect），χ2=0，df=0，p=1。12所学校的单元均值信度和总均值信度的点估计值、标准误，以及用Raykov等人的方法和本文介绍的新方法求得的置信区间如下表所示。

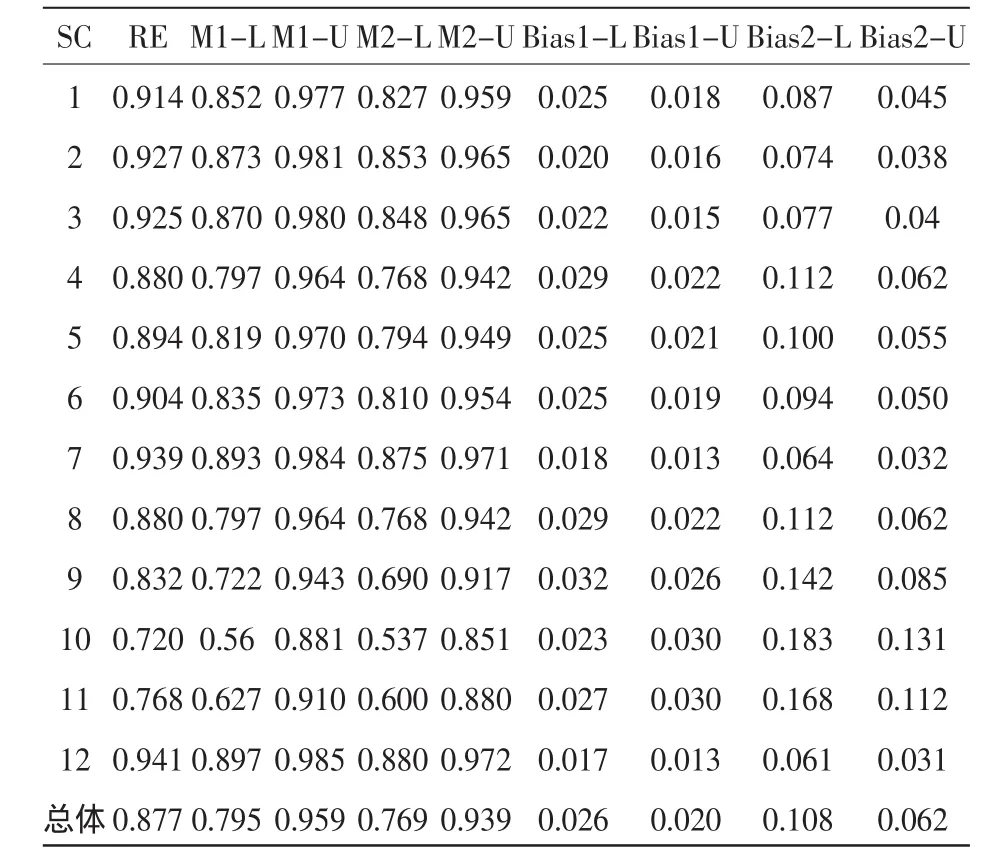
12所学校的单元均值信度和总均值信度的点估计值、标准误及置信区间

由上表我们可以看出，相比于本文介绍的新方法，Raykov等人介绍的求置信区间的方法有较大的偏差，下限差值最大的达0.032，最小也为0.017（见表中的Bias1-L列）；上限差值最大的达0.030，最小也为0.013，（见表中的Bias1-U列），因此Raykov等人介绍的方法在求置信区间时有较大的偏差。同时，用Raykov等人介绍的方法求得的置信区间的下限到信度点估计值的距离，与上限到点估计值的距离并不相同（见表中的Bias2-L列和Bias2-U列），差值最大的达0.056，最小的也有0.030，可见，Raykov等人介绍的求置信区间的方法不准确。相对而言，本文介绍的新方法求阶层线性研究中信度的置信区间更简单，也更精确，即用Delta法求的信度的置信区间后，直接用p±1.96SE来求信度的置信区间。

六、小结

从信度置信区间的设定与分析结果可信性的关系看，如果信度置信区间的上限小于设定的可接受的信度水平，那么此次测量的质量不高，后续统计分析的结果不可信。如果信度置信区间的下限大于可接受的信度水平，那么此次测量的质量较高，后续统计分析的结果可信。如果可接受的信度水平包含在信度置信区间中，那么此次测量的质量值得怀疑。

简单而精确是一种方法的生命力所在。相比于Raykov等人所介绍的两水平研究中信度置信区间的估计方法，本文介绍的新方法，简单而又精确，一般的应用工作者很容易掌握。

值得一提的是，在两水平研究中还有一个信度，即测验信度。目前，比较好的估计两水平研究中单维测验信度的方法，是基于两水平验证性因子分析推导出来的信度系数。λj和λ与测验信度不同，主要体现在四个方面。（1）本质不同。信度λj和λ指的是参数统计估计的精确性，λj和λ是两个统计值。测验的信度则用来衡量测验的稳定性和一致性程度，测验信度值越小，表示测量误差越大，测验质量不高。（2）基于的模型不同。λj和 λ是基于多层线性模型（multilevel linear model），而测验信度是基于两水平验证性因子模型。（3）信度数目不同。在两水平研究中，λj数目对应着第二水平的组个数，第二水平有多少个组，就有多少个λj，整个两水平研究只有一个λ，λj与λ的个数与研究中所用的测验数目无关。测验信度则与测验相对应，两水平研究中有多少个测验就有多少个测验信度。（4）信度值变化。在两水平研究中，如果多层线性模型的变量发生变化（增加或减少变量），λj和λ的值可能变化。测验信度则与研究中是否加入其他测验无关，即一个测验信度独立于另一个测验信度。因此，我们不能混淆λj，λ与测验信度。研究者在进行两水平研究时，可同时估计λj，λ和测验信度，从而获取更多关于研究可靠性方面的信息。

［1］杨英，龙立荣，周丽芳.授权风险考量与授权行为：领导－成员交换和集权度的作用［J］.心理学报，2010（42）：875～885.

［2］Bonett，D.G.Varying coefficient meta-analytic methodsforalphareliability［J］.Psychological Methods，2010（15）：368～385.

［3］Woods，C.M.Confidence intervals for gamma-family of ordinal association［J］.Psychological Methods，2007（12）：185～204.

［4］［13］叶宝娟，温忠麟.单维测验合成信度三种区间估计的比较［J］.心理学报，2011（43）：453～461.

［5］Zou，G.Y.Towards using confidence intervals to compare correlations［J］.Psychological Methods，2007（12）：399～413.

［6］Heck，R.H.，&Thomas，S.L.An introduction to multilevel modeling techniques［M］.New York：Routledge，2009.

［7］［14］Raykov，T.，&Penev，S.Evaluationofreliability coefficientsfortwo-levelmodelsvialatentvariableanalysis［J］.StructuralEquationModeling，2010（17）：629～641.

［8］张雷，雷雳，郭伯良.多层线性模型应用［M］.北京：教育科学出版社，2003.

［9］Raudenbush，S.W.，&Bryk，A.S.Hierarchicallinear models.Applications and data analysis methods（2nd ed.）［M］.ThousandOaks，CA：Sage，2002.

［10］Laenen，A.，Alonso，A.，Molenberghs，G.，&Vangeneugden，T.A family of measures to evaluate scale reliability in a longitudinal setting［J］.Journal of the Royal StatisticalSociety，2009（172）：237～253.

［11］Laenen，A.，Alonso，A.，Molenberghs，G.，&Vangeneugden，T.Reliability of a longitudinal sequence of scaleratings［J］.Psychometrika，2009（74）：49～64.

［12］Raykov，T.，&Penev，S.Estimation of maximal reliability for multiple-component instruments in multilevel designs［J］.British Journal of Mathematical and Statistical Psychology，2009（62）：129～142.