神经网络分析与相关分析、回归分析的比较——基于大学毕业生的成就性水平及其影响因素的研究

一、引 言

在社会学定量研究中经常遇到多个自变量与因变量之间复杂关系的分析。通常使用的方法是多元回归分析或路径分析。但是，多元回归分析或路径分析模型都是基于线性关系假设建构的。而现实生活中变量之间往往是非线性关系，因此线性分析难于真实反应变量之间的关系，甚至会将具有很强非线性关系的变量视为无关，且在多元回归分析或路径分析中由于多重共线性的原因难以纳入更多的变量。在多变量之间因果关系的分析中如何在方法上有所突破是社会学定量研究中面临的一项难题。本研究尝试计算机神经网络分析的方法，以毕业生的成就性水平为输出变量，以众多影响因素为输入变量，通过训练神经网络模型对大学毕业生的成就性水平及其影响因素的关系结构进行计算机模拟，希望能够对影响个人社会地位实现的复杂、多变量之间的关系做出更有效的解释。

自1943年McCulloch和Pitts根据生物神经元的一些基本生理特征提出简单的人工神经元数学模型与构造方法至今[1]蒋宗礼：《人工神经网络导论》，〔北京〕高等教育出版社2001年版，第11页。，神经网络分析方法得到了很大的发展。90年代以来，随着自身局限性的问题得到解决，神经网络研究方法在自然科学领域、工程技术、医学、商业、心理学等众多领域中已经得到了广泛的应用，解决了很多传统科学技术解决不了的难题。它为人类认识世界、开拓未知领域、提高现代科学技术研究水平起到了很好的促进作用。随着神经网络技术的发展，近几年在经济管理领域有了较多的应用。沈国琪等构建了BP神经网络预测模型，对失业状况进行预测,并与多元回归预测模型的预测结论进行比较,结果发现BP神经网络预测模型的预测性能高于多元回归预测模型[1]沈国琪、陈万明：《基于多元线性回归与BP神经网络分析的失业预测建模实证研究》，〔长春〕《工业技术经济》2014年第2期。。金代志等构建了基于BP神经网络的顾客价值识别模型并进行了仿真实验，证明构建的BP神经网络模型适合对企业的顾客价值进行识别[2]金代志、王春霞、石春生：《基于BP神经网络的顾客价值识别研究》，〔北京〕《中国软科学》2009年第7期。。陈敏等利用重构相空间的嵌入维数建构了算法与设计相对简单的将混沌理论和神经网络相结合的居民消费价格指数预测模型[3]陈敏、曹文明、李泽军：《基于混合神经网络和混沌理论的居民消费价格指数预测研究》，〔武汉〕《统计与决策》2009年第15期。。秦迎林等针对当前第三方物流企业资源整合风险预警定量方法的匮乏，探讨了一种基于BP神经网络的评价模型。并通过对样本的训练验证了所建立的BP神经网络模型在物流资源整合风险预警中具有较高的实用价值[4]秦迎林、李红艳：《基于BP神经网络的第三方物流资源整合风险预警模型》，〔武汉〕《统计与决策》2009年第7期。。

神经网络分析的应用范围极为广泛，如D.Lowe和M.Tipping将前向神经网络分析方法运用于地质学，充分显示出了神经网络分析在处理高维数据中的优势[5]D.Lowe&M.Tipping 1996，“Feed-Forward Neural Networks and Topographic Mappings for Exploratory Data Analysis”,Neural Computing and Applications 4.。W.Z.Lu等人将粒子群优化模型引入了对香港污染级别及趋势的预测，显示出这种新的神经网络分析模型在分析实际空气污染问题时的可行性和有效性[6]Weizhen Lu,H.Y.Fan&S.M.Lo 2003,“Application of Evolutionary Neural Network Method in Predicting Pollutant Levels in Downtown Area of Hong Kong”,Neurocomputing 51.。Hokky Situngkir试图运用神经网络方法弥合社会学的二元对立问题[7]Hokky Situnqkir 2003,“Emerging the Emergence Sociology:The Philosophical Framework of Agent-Based Social Studies,”Journal of Social Complexity 2.。M.Girvan等人提出了一种新的计算网络结构的方法，利用边中介性计算社区网络结构，他们特别关注由网络节点紧密结合成群体而群体之间松散联系的社区。通过与传统方法的比较，验证了这种方法构建的计算机图具有很强的敏感性和可靠性[8]Michelle Girvan&M.E.J.Newman 2002,“Community Structure in Social and Biological Networks”,Proceedings of the National Academy of Sciences of the United States of America 99.。

在我国，虽然在经济管理领域神经网络的应用已经取得了不少成就，但在其它人文与社会科学领域中，神经网络研究方法的成功应用仍然属空白。在社会学实证研究中，由于社会统计方法的限制，某些情况下变量之间的相关性并不能得到很好的解释，因此将神经网络研究方法应用于社会科学实证研究，在方法的创新上是一个有益的尝试。

二、数据来源与变量的选取

1.数据来源

本研究所使用的数据来源于哈尔滨工业大学2004年至2005年期间进行的毕业生状况调查的数据。本研究截取1977年恢复高考以后的20届毕业生为研究对象，入学年限跨度为1977年到1996年。由于分析涉及的变量较多，而且要求分析的个案在任何变量上都不能有缺失值，因此满足本研究的个案数为501个。由于1977年至1996年是我国从计划经济向市场经济转型的变迁时期，而在这一时期哈尔滨工业大学是一个在我国名列前茅的理工科大学。因此本文的研究结论只对于国家重点的理工科大学毕业生具有参考价值。

2.大学毕业生成就性水平指标体系的建构

（1）指标的选择及赋值。成就性水平是指个人在社会体系中所拥有的地位、权势、财富或声望的总和。本文中成就性水平的指标由下述变量构成：社会地位指数、收入在单位中的相对水平、目前住房的使用面积、2004年总收入、岗位在单位中的重要性、获奖指数六个变量构成。

（2）基于主成份分析的指标合并。由于上述表示个人成就性水平的指标不仅多，而且包括了不同测度层次的变量。本文应用主成份分析的方法对上述指标降维处理。主成份分析需要变量之间具有较强的相关关系，因此需要对变量是否适合于作主成份分析进行检验。采用KMO方法进行检验的结果是KMO值为0.724，显著性水平为0，这说明变量之间有较强相关，适合做主成份分析。

在主成份分析中按照变量的数量提取主成份的个数，即提取6个主成份。这6个主成份特征值及方差贡献率的分布见表1。以每个主成份的方差贡献率为权数，计算主成份得分的加权平均值，这样可以将不同测量水平，不同单位的变量综合成为一个主成份得分，该主成份得分称为成就性水平得分，分数的大小可以反应个体成就性水平的高低，其计算公式为：

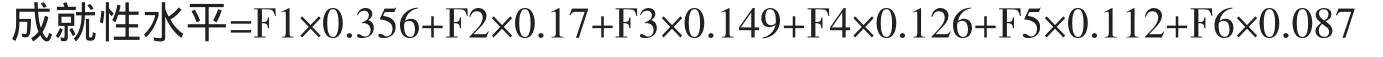
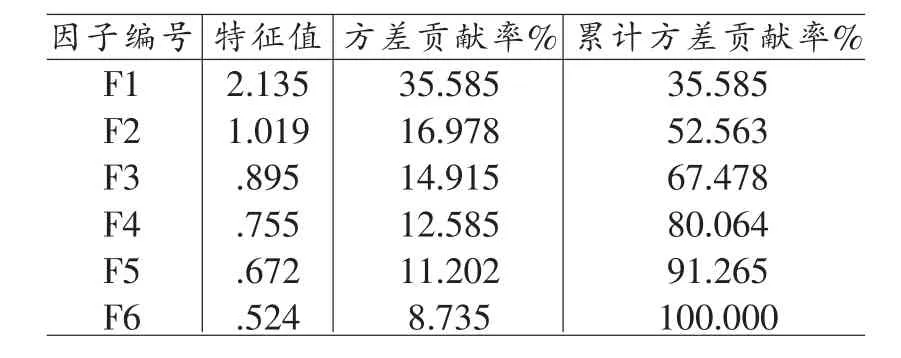
表1 被因子解释的总方差

3.影响因素的变量选择

本研究根据经验判断从先赋因素和致获因素两方面共选择了对毕业生的成就性水平可能产生影响的22个变量，外加时间变量。时间变量为：本科入学至调查时的年限；先赋因素为：读本科时家庭经济状况（当时的社会平均水平）、父亲的职务级别、父亲的职称、父亲的政治面貌、父亲的文化程度、母亲的职务级别、母亲的职称、母亲的政治面貌、母亲的文化程度、上大学前主要居住地区类型；致获因素为：最后学历、政治面貌、高考成绩与重点分数线的差、本科时的学习成绩在班级的排名、本科时学习刻苦程度、本科时担任学生干部的级别、本科时担任学生干部的时间长度、本科时获得奖励的级别、本科时所在班级获得奖励的级别、本科时参加课外活动情况、读本科时的人际交往情况、读本科时的人际关系情况。由于人际交往和人际关系的测量比较困难，本研究采用“读本科时您愿意和寝室的多少人交往”作为人际交往的指标，“读本科时您寝室有多少人愿意和您交往”作为人际关系的指标。

三、BP神经网络分析的原理

1.BP神经网络模型的结构

BP（Back Propagation）神经网络模型是模仿人的大脑建构的仿真模型，由神经元和神经元的连接构成神经网络。每个神经元都可以接受来自其它神经元的输入，并计算出输出，这些输出也可以成为其它神经元的输入。一般具有输入层、隐含层、输出层三个部分,网络结构如图1所示。输入层的每一个神经元都对应着一个输入变量xi，这些变量的值也称为网络输入。隐含层中可能包含一层也可能包含多层神经元。输出层因应用目的不同可以有多个输出神经元，也可以只有一个输出神经元。图中的w、v是权值。每个神经元在接受输入信息时将输入数据与权值相乘以后进行计算，然后向下一层神经元输出。

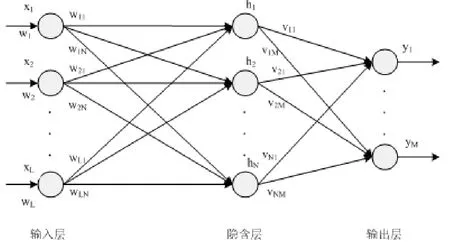
图1 BP神经网络模型

本研究中，输入层神经元的个数与影响因素变量数相同，共为23个。输出层神经元个数与因变量数相同，本研究只有一个因变量，因此输出神经元为1个。隐含层包含的层数和神经元个数由研究者来确定。由于隐含层层数和隐含层神经元个数的不同将会影响到神经网络模型拟合优度。因此为得到最优的神经网络模型必须首先确定隐含层的层数和隐含层神经元个数。根据经验，初步设定第一层隐含层的神经元个数为输入层神经元个数的二分之一，第二层隐含层的神经元个数可以为第一层的二分之一，以此类推。每次训练以后软件可以提供拟合优度和每个神经元对输出结果的贡献率。如果存在贡献率特别小的神经元，就减少神经元的个数。隐含层层数和隐含层神经元个数确定的方法是在设定同样的迭代次数（本研究中的迭代次数为50000次）的情况下选择拟合优度最好的模型。

本研究采用Qnet神经网络分析软件，经过多次训练不断调整，最终确定的神经网络模型为：输入层包含23个神经元，第一隐含层包含12个神经元，第二隐含层包含6个神经元，输出层为1个神经元。网络结构如图2所示。

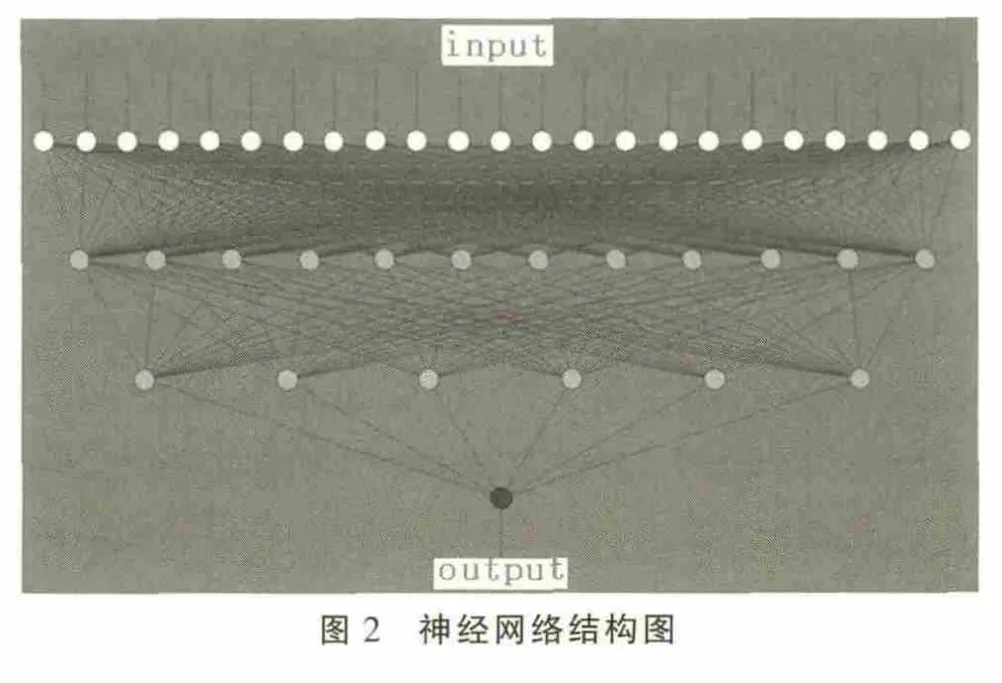
2.BP神经网络模型的训练过程

使用神经网络来分析因变量与自变量之间关系时，将因变量的观测值视为网络的期望输出，也称为目标变量。自变量的观测值即是网络输入。神经网络模型根据网络输入计算出的结果称为网络输出。网络输出与期望输出的差即为误差。神经网络模型依据误差反向传播算法来消除误差。在正向传播阶段,输入层神经元将输入数据计算后传递给隐含层神经元，隐含层神经元接收到这些数据后经过计算再传递给输出层神经元，每一层神经元的状态只影响到下一层神经元的状态。输出层会将网络输出结果与因变量的观察值进行比较。当差值超过误差允许范围时,进入误差反向传播阶段,误差信号按原来的连接通路返回,同时对各层之间的连接权值进行调整,直到系统误差可以接受为止,此后权值不再改变。这个过程也称为神经网络模型的训练过程。

在这里我们要特别说明神经网络模型的拟合优度问题，由于初始化时网络的权值是系统随机赋予的。所以，即使用同一个网络结构，同一组数据训练出的神经网络是不唯一的。但差异不会太大。为了更好的判定神经网络模型的拟合优度，应进行多次重复训练。本研究进行了33次重复训练，拟合优度最好时为0.82，最差的也达到0.71。33次训练的平均拟合优度为0.76。

四、神经网络分析结果

神经网络模型训练结束以后，系统会给出每个输入神经元对输出变量的贡献率。系统将全部输入变量对输出变量的贡献率视为100%。通过比较每个输入神经元对输出的贡献率来确定输入变量对输出变量影响作用的大小。本研究中有23个输入变量，平均每个输入变量对输出变量的贡献率为4.35%。如果某个输入变量的贡献率大于该值就可以认为该输入变量对输出变量有较大影响。

她跟他们混了这些时，也知道总是副官付帐，特权阶级从来不自己口袋里掏钱的。今天出来当然没带副官，为了保密。

由于输入神经元对网络输出的贡献率受到每次训练时输入神经元权值的初始赋值影响，每次训练得到的贡献率并不相同。为了更好的判定每个影响因素变量对成就性水平影响程度的大小，用每个输入神经元在33次训练中的平均贡献率作为其对输出变量影响的指标。为清晰展现不同影响因素对大学毕业生成就性水平的作用，利用23个影响因变量的平均贡献率绘制了图3。

从图3中可以看出，引入模型中的影响因素作用可以分为四个层次。处于第1个层次的是前三个变量，它们对输出变量的贡献率明显大于其它变量，这三个变量的作用依次递减，差异也很大。处于第2个层次的变量是第4到第10的变量，它们对输出变量的贡献率虽然依次递减但相互差异不大。处于第3个层次的变量是第11到第19的变量，这些变量的作用几乎处在一个水平线上。处在第4个层次上的变量是第20到第23的变量，它们对成就性水平的影响很微弱。于是我们得到如下结果：

1.家庭经济状况对大学毕业生成就性水平具有重要影响

神经网络分析结果表明，在所有的影响因素变量中“读本科时家庭经济状况”高高的居于第一位。它对输出变量的贡献率为9.11%，大约是第二个层次变量的2倍。这与我们一般的理解与感受是相悖的结论，也是一个令人沮丧的结论。一般的认为，经过十几年的寒窗苦读考入了重点大学的学生们有能力把握自己的前途和命运，家庭的影响应该渐渐地淡去。可分析结果却告诉我们家庭经济状况却如影随形地伴随着他们，甚至影响着大学生毕业十几年、几十年后的成就性水平。

那么，“读本科时家庭经济状况”是如何影响成就性水平的呢？采用方差分析的方法分析家庭经济状况与毕业生成就水平的关系，结果如图4所示。从图中可以看出“读本科时家庭经济状况”与成就性水平的关系并非是线性的。多重比较的方差分析表明，家庭比较富裕的毕业生成就性水平与其它四个类别的毕业生有显著差异。显著性水平为0.01。由于填答“非常富裕”的只有两个个案，该类别的情况不具有推论价值。总的看来，比较富裕家庭的毕业生取得了相对比较高的成就性水平。令人比较欣慰的是，家庭经济状况一般、比较贫困和非常贫困的毕业生成就性水平没有显著差异。尤其是家庭非常贫困的毕业生成就性水平还略高于平均值。说明贫困并没有成为毕业生获取成就的抑制因素。

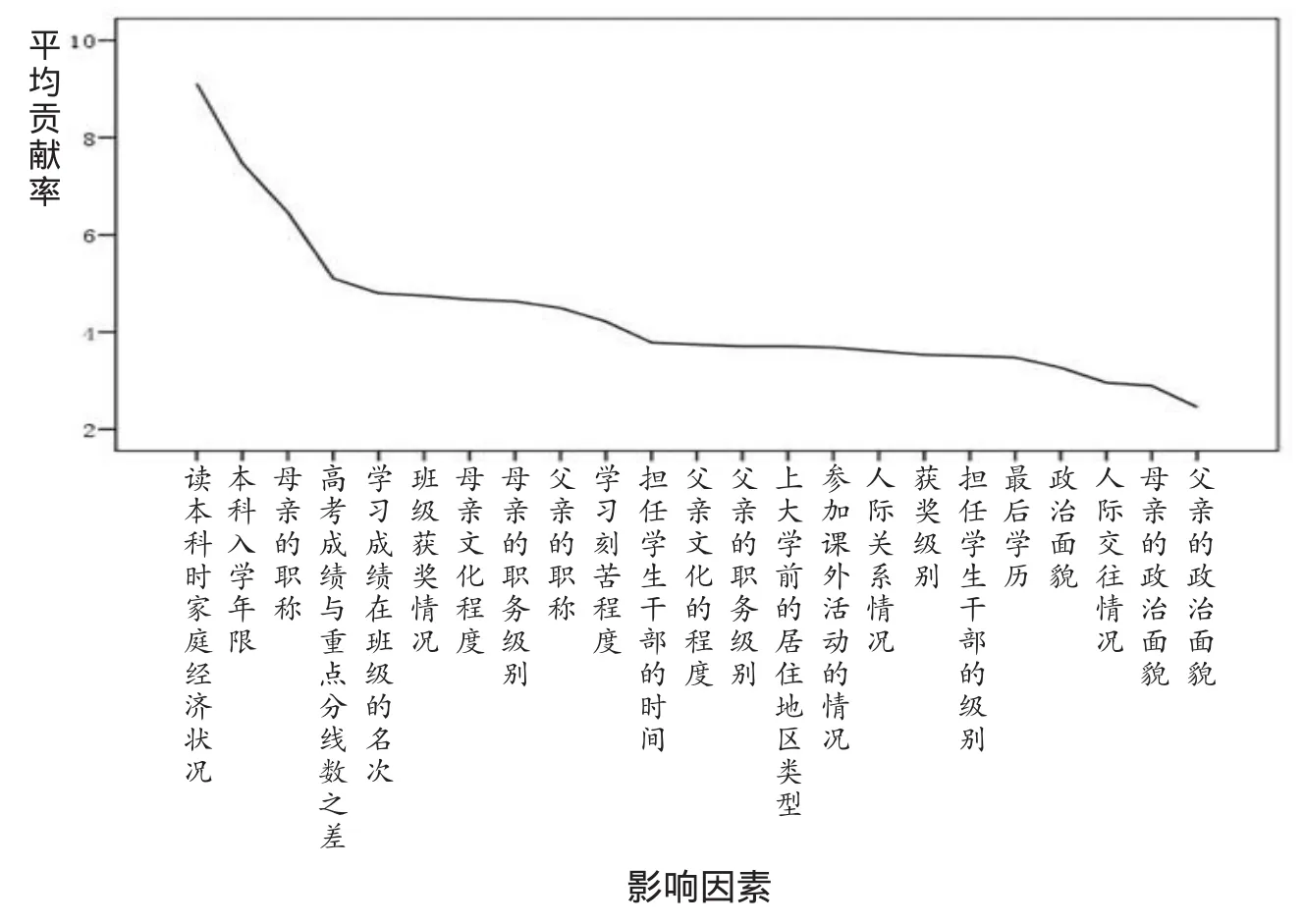
图3 成就性水平影响因素变量的贡献率

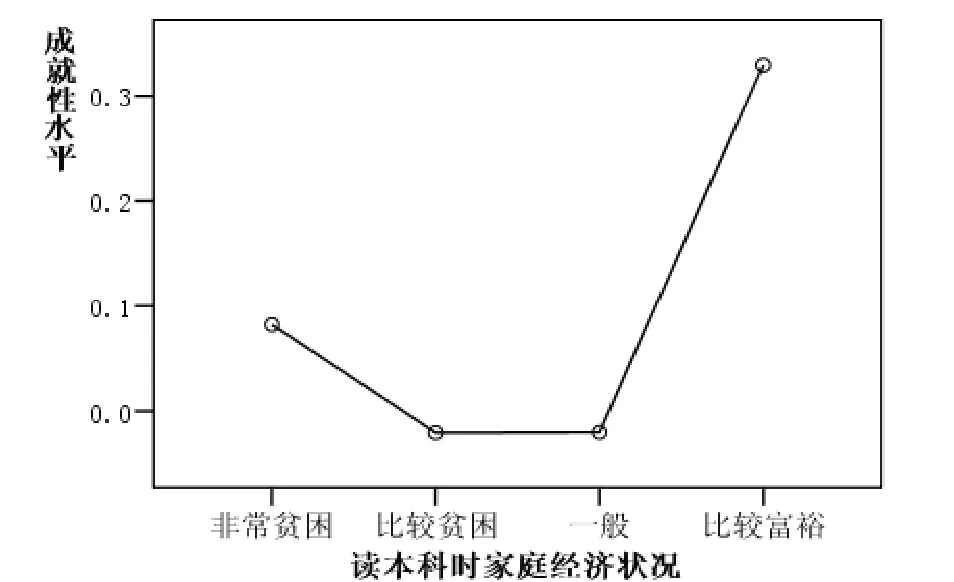
图4 家庭经济状况与成就性水平的相关图

2.入职的前十五年对毕业生成就性水平具有决定性的作用

对成就性水平影响作用排在第二位的变量是“本科入学年限”。这个变量表明的是工作时间对成就性水平的累积作用。将入学年减掉4年即可换算成工作年限。考虑到工作年限对成就性水平的作用需要一定的累积时间，本文中将1977、1978、1979年入学的毕业生工作年限作为一个时间段，其后每五年为一个时间段。并将工作时间段与毕业生的成就性水平进行方差分析，结果图5所示。方差分析的F值为16.9，显著性水平为0.000.说明不同工作年限的毕业生成就性水平有显著差异。

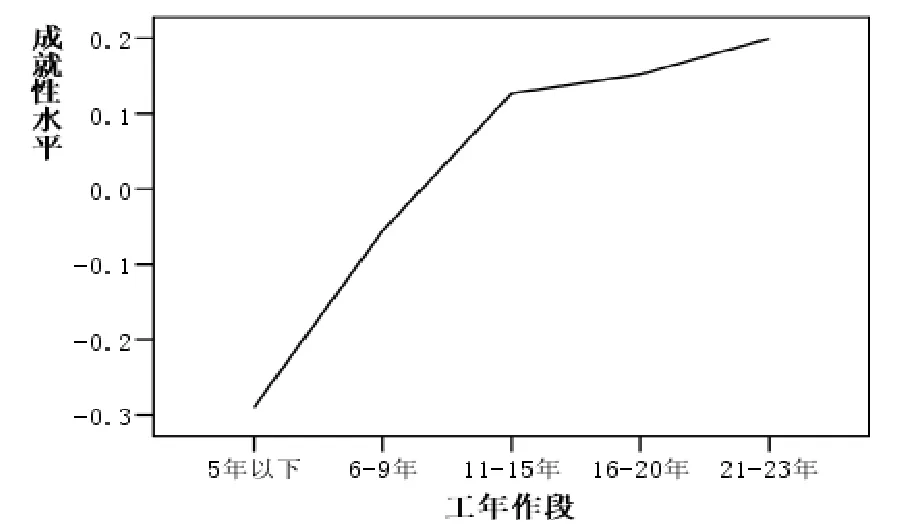
图5 工作年限与成就性水平的相关图

总的看来是工作时间越长，对成就性水平的积累作用越强。但其成就性水平也不是随着工作年限的增加而线性增长。毕业后的前15年成就性水平增长较快，其后虽有增加，但增加的已相对较缓慢。也就是说，大学毕业生入职的前15年对于其一生所能实现的最高的社会地位具有决定性的作用。

3.母亲对子女成才的作用远远大于父亲

由于布劳与邓肯的模型中只纳入了父亲的变量，而没有纳入母亲的变量。因此，我国学者的研究也大都以父亲代表家庭的社会地位来研究其对子代社会地位获得的影响。为此，我们特别关注了母亲对子女社会地位获得的影响问题[1]郭志坚：《社会出身与地位获得：代际流动研究新进展》，〔广州〕《青年探索》2005年第6期。。本研究利用神经网络分析的优势，将父亲与母亲的变量同时纳入模型来分析家庭社会地位对子代的影响，同时比较父亲和母亲各自作用的大小。研究中对于毕业生的父母都选择了文化程度、职务级别、职称和政治面貌四个变量进入模型。分析结果发现父亲、母亲的四个对应变量，母亲都排在父亲的前面。四个变量对成就性水平的总贡献率母亲也大大的超过父亲。如表2所示。这意味着母亲对子女成才的影响明显大于父亲。

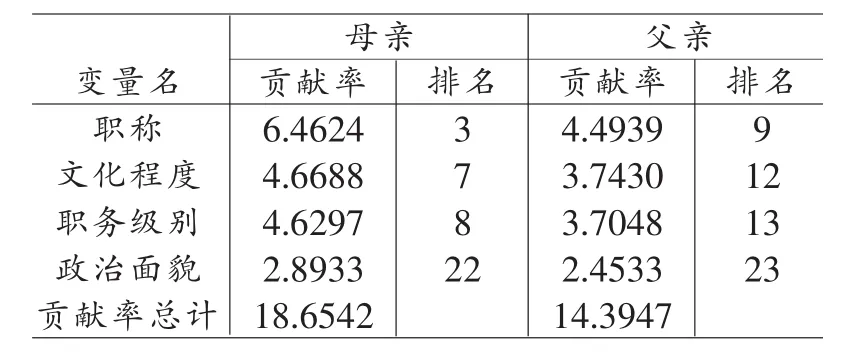
表2 父亲、母亲变量对成就性水平贡献率的比较

4.先赋性因素对毕业生成就性水平的影响大于致获性因素

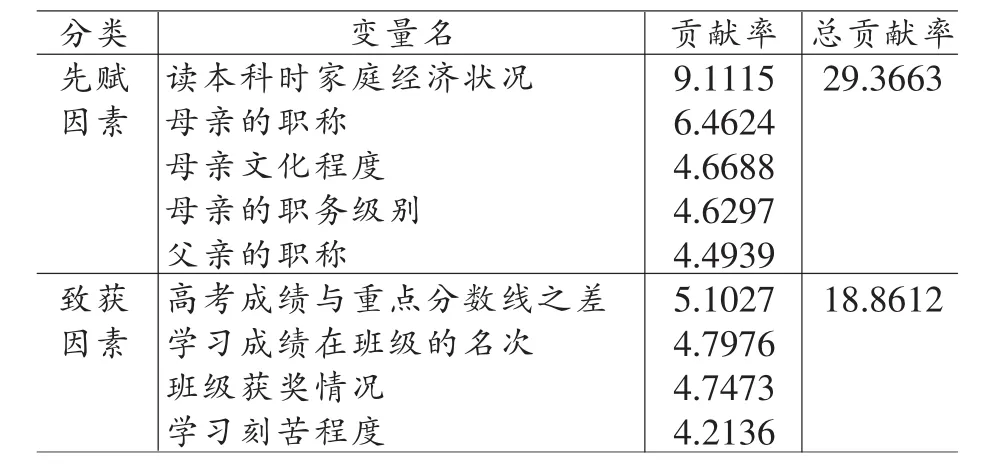
表3 先赋因素与致获因素对成就性水平影响作用的比较

5.学业性因素对毕业生的成就性水平的影响大于非学业性因素

神经网络分析结果表明，毕业生的“高考成绩与重点分数线之差”、“学习成绩在班级的名次”和“学习刻苦程度”这三个学业性因素的变量对毕业生成就性水平的贡献率都处在影响较大的第二个层次上。而“担任学生干部的时间”、“参加课外活动的情况”、“人际关系情况”、“担任学生干部的级别”等非学业性因素的贡献率都处在第三个层次上。这说明，学生在读本科期间的学业性因素对未来成就性水平的影响要大于非学业性因素。

6.优秀班级的学生取得了较好的成就性水平

在神经网络分析模型中，“班级获奖情况”是排在第六位的影响因素。其对毕业生成就性水平的贡献率为4.75%，仅次于学习成绩。没有获过奖的班级一般为普通的班级，而获得省部级及以上奖励的班级往往是优秀班级。统计分析表明，普通班级和较好的班级的学生成就性水平没有显著差异，而优秀班级的学生毕业后的成就性水平明显高于普通班级的学生。可见班风对学生的影响还是很大的。这个结论也提示了大学管理要重视班风的建设。

7.大学毕业生社会地位获取的过程中出现了去政治化倾向

本研究中将父母及毕业生的政治面貌作为影响因素引入模型，但这三个变量对成就性水平的贡献率都很低。父母的政治面貌排在倒数第一、第二，毕业生本人的政治面貌排在倒数第四。它们对毕业生成就性水平的影响都很微弱。这个结果有些出乎意料。被调查的学生都毕业在80或90年代，当时的政治身份在就业、提升等方面都起着重要的作用。因此，笔者假设这几个变量都应该对毕业生成就性水平产生较大影响。但分析结果表明政治身份对个人成才的影响已经很小。改革开放的社会环境淡化了政治身份的作用。大学毕业生获取社会地位的过程中出现了去政治化倾向。

五、神经网络分析与相关分析的比较

为分析神经网络分析方法的优势与不足，将神经网络分析结果与相关分析方法进行比较。表4的第4列给出了成就性水平与影响因素的相关系数。由于成就性水平是一个尺度变量，如果影响因素变量也是尺度变量，就采用线性相关分析，如“本科入学年限”、“高考成绩与重点分数线之差”两个变量与成就性水平的相关分析的结果是给出皮尔逊相关系数。其它的影响因素变量都是有序类别变量，它们与成就性水平的相关分析的结果是给出相关比率，即Eta值。从表4中可以看出，神经网络分析的结果与一般相关分析的结果不太一致。比如表中排在第三位到第十位的变量都是在神经网络分析中对“毕业生的成就性水平”影响较大的变量，但相关分析的结果是他们与因变量不存在显著相关。相关分析中与“成就性水平”达到0.01显著性水平的几个变量，如“担任学生干部的时间”、“父亲的职务级别”、“ 参加课外活动的情况”、“ 最后学历”在神经网络分析中对因变量的贡献并不大。原因是神经网络分析注重的是神经网络输出与期望输出达到最终的拟合优度时，输入变量的贡献率。而线性相关分析表明的是当影响因素变量发生变化时因变量是否也发生变化。如果两个变量是非线性的关系，线性相关会存在过度简化的问题，无法体现出两个变量的复杂关系，甚至会把较强的非线性相关视为不相关。在社会学研究中变量之间存在线性相关的情况是比较少的，线性相关分析不能很好地描述两个变量之间的复杂的相关关系。相关比率Eta表现的是当影响因素取不同值时成就性水平的平均值是否有差异。由于比较的仅仅是平均值，仍然存在过度简化的问题。对于不同的个案，影响因素变量取相同值时对成就性水平的影响可能是不同的。如家庭比较富裕可能给子女提供了更好的向上流动的条件而使子女获得了较好的成就性水平，也可能使子女坐享其成缺乏上进心成为纨绔子弟。不论是线性相关分析还是相关比率分析都不能表现这种复杂的影响作用。相比之下，神经网络分析则表现出了明显的优越性。这就是神经网络分析与相关分析结果不一致的原因。

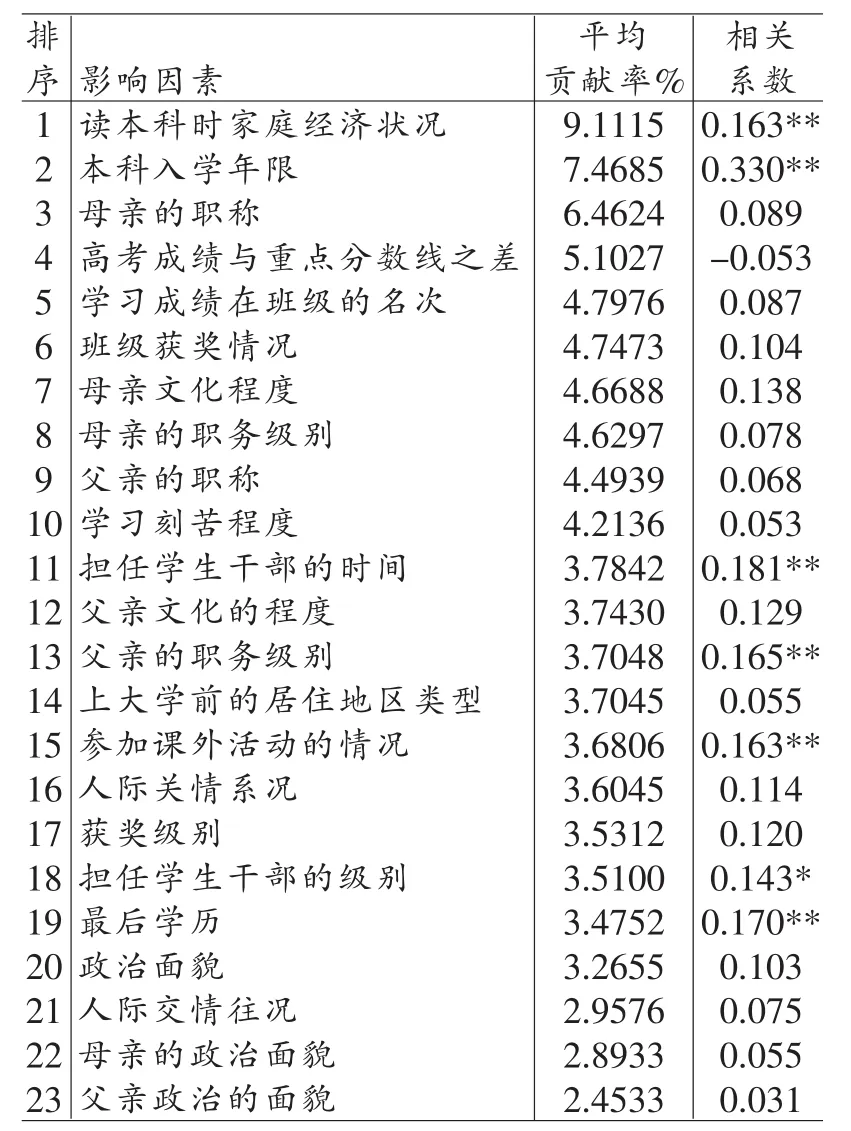
表4 神经网络分析与相关分析比较

六、神经网络分析与多元回归分析的比较

就本研究的变量来看，用多元回归分析也是比较适合的方法。对变量进行标准化处理以后，自变量均已转化为尺度变量。为比较神经网络分析与多元回归分析的差异，以毕业生的成就性水平为因变量，以23个影响因素为自变量，采用逐步剔出的方法引入回归模型，进行多元回归分析结果如下：

从表 5、表 6、表 7中可以看出，分析过程中剔除了17个对因变量影响不显著的自变量，最后的模型中只保留了6个自变量。这6个自变量中还有1个达不到0.05的显著性水平。多元线性回归分析要求自变量与因变量之间是线性相关，同样存在过度简化的问题。对于自变量与因变量之间存在的较强的非线性关系，多元线性回归分析无能为力。如果因变量的影响因素众多，而且这些影响因素与因变量之间的关系是否线性很难确定，采用多元线性回归的方法难于准确描述变量之间的关系。在这种情况下神经网络分析方法则显现出更大的优势。

表5 模型概要

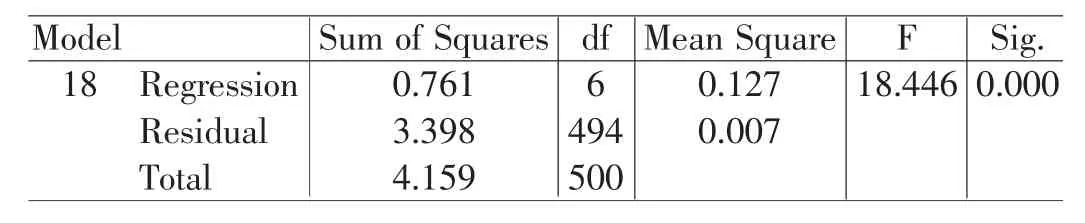
表6 方差分析

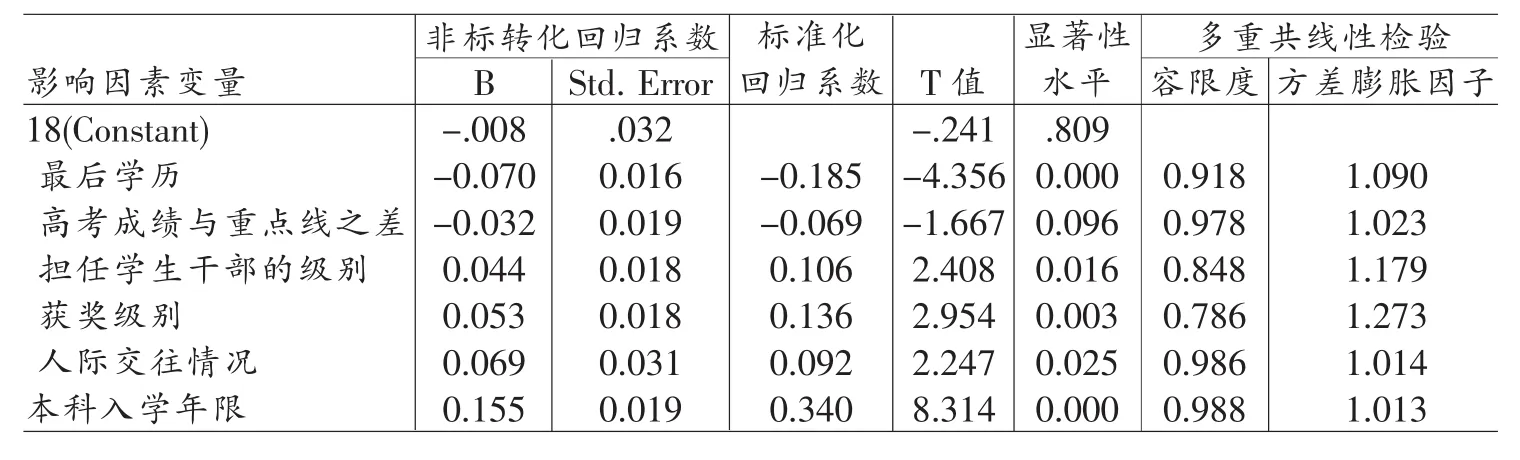
表7 回归系数

七、神经网络分析方法的优势与不足

多变量之间的因果关系的分析是一个复杂的过程，用神经网络分析方法来分析社会现象的复杂关系既有明显的优势，也存在一定的缺陷。神经网络分析方法的优势在于：第一，如果样本足够大，网络结构设置合理，它能很好地模拟出变量之间的作用机制。尽管这种机制是以黑箱的形式存在的，但是网络输出与期望输出的高拟合优度可以说明网络运行对现实的变量关系具有很高的仿真性。这样，如果样本量足够大，数据具有足够高的信度，就有可能对社会现象给出精度较高的预测。第二，神经网络分析软件可以输出神经网络的拟合情况、误差情况、各层和各神经元的有关信息，为分析自变量与因变量的关系提供了丰富的数据。第三，统计学的分析方法大都是以线性分析为基础，而现实中变量之间的关系为线性的很少，这就必然存在的对变量关系的简化和信息的丢失。而神经网络分析则不存在这样的简化，对于变量间非线性的关系它也能做到很好的模拟，它所反映出的变量之间的关系能够更接近于现实。第四，神经网络对变量取值的要求不高，也不要求变量必须服从一定的分布或具有等方差性，只要是有序类别变量并可以被标准化，即可以应用。

对神经网络分析方法优势的肯定并不意味着它毫无缺陷。首先，由于它是模拟人脑的工作机制以黑箱的形式完成了运算过程，不能将变量之间的复杂关系直接展现出来。第二，通过输入层神经元的贡献率来分析输入变量与输出变量之间的关系时，不能明确输入变量的作用方向，甚至无法知道输入变量对输出变量的影响是负的还是正的。如果要想明确每个变量的作用机制还需进行更复杂的MIV分析。第三，神经网络分析的初始化是对各个神经元的权值在[-1,1]之间随机赋值。这就使得在条件完全相同的情况下训练出来的网络是不唯一的。本研究是用33次训练的平均值来进行分析的。相比之下，统计分析只要使用的是同一组数据建构出来的模型是唯一的。另外，对于无序类别变量目前还无法引入到神经网络分析中，这是一个不小的遗憾。对于神经网络分析方法的缺陷与不足还有待于研究者在今后的应用中去不断的探索和完善。