基于旋转模型的青藏高原重力变化研究

2014-04-18李立功段虎荣牛丽娟

地理空间信息 2014年4期

关键词：重力场块体青藏高原

李立功，段虎荣，牛丽娟

（1.陕西铁路工程职业技术学院, 陕西渭南 714000；2.西安科技大学测绘科学与技术学院，陕西西安 710054）

基于旋转模型的青藏高原重力变化研究

李立功1，段虎荣2，牛丽娟1

（1.陕西铁路工程职业技术学院, 陕西渭南 714000；2.西安科技大学测绘科学与技术学院，陕西西安 710054）

用数值模拟方法研究了地壳旋转运动与空间重力变化的关系，得出地壳划分的长方体的旋转运动引起的重力变化呈中心对称分布。青藏高原地区的研究资料表明，该区域绕青藏高原东构造存在顺时针旋转运动。文中结合该地区的数字高程以及GPS观测速率数据，计算了青藏高原块体旋转运动引起的重力变化，并与GRACE卫星重力观测结果进行了对比分析。

构造；卫星重力；旋转运动；重力变化

青藏高原是世界上海拔最高、最年轻、动力学环境最复杂的高原，是地学研究的热点。卫星重力探测技术以其快速、高效、几乎覆盖全球并能给出大尺度的重力变化等特点，大大改善了人们对地球重力场的认识[1-4]。与传统的重力观测理论不同，现有的重力变化理论模型大都不太适合解释卫星重力观测到的结果[5]。为此，本文建立了地壳旋转模型，尝试通过模型的旋转运动来模拟地壳运动，进而对引起的重力变化进行分析解释。

1 旋转模型及计算方法

1.1 地壳旋转产生的重力变化

由万有引力定律可知，在重力场中，对于某个相对固定的观测点（ε，η，ζ），点源物质位移时产生的重力变化为[6]：

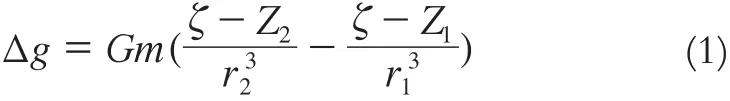
式中，G表示地球引力常数；m表示点源物质的质量；r1、r2分别表示位移前后观测点到点源物质的距离。

在进行地质体实际研究时,可将地质体分成若干个规则的长方体[5]，每个长方体可以理解为由n个点源物质组成。根据式（1），对第i个长方体运动进行积分，就可以得到该长方体发生位移时在空间某处产生的重力变化[6]。

式中，ρ表示介质密度；V表示长方体的体积。

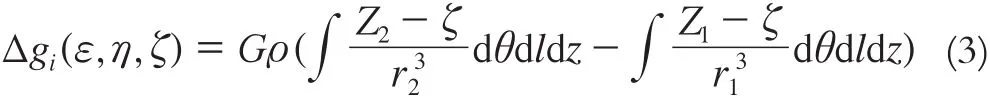
根据式（2），当直立长方体做旋转运动时，为便于数据处理计算，不妨在建模时，将直立长方体的2个底面建立为正方形，设其底边长为2l，棱长为2h。此时，在相应空间点处的重力变化为：式中，θ为长方体旋转运动所转过的角度，θ ∈[0,2π]。设（XC，YC，ZC）为长方体中心点坐标，则X1，X2∈ [XC-l，XC+l]，Y1，Y2∈ [YC-l，YC+l]，Z1，Z2∈ [ZC-h，ZC+h]。

由重力的可加性知，所有长方体的旋转运动引起空间点（ε，η，ζ）处的重力变化为：

1.2 GRACE卫星观测数据计算重力变化[5,7]

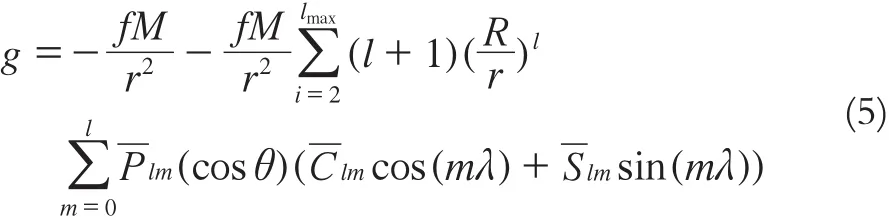
GRACE卫星采用高-低和低-低SST两种模式进行探测，可以精确测定地球重力场的中、长波部分的变化。在正常椭球情况下,对地面某点（r，θ，λ）处的地球重力位球函数r求导，可得：式中，Plm (c osθ)为完全规格化l阶m级缔合Legendre多项式；fM为地球引力常数为完全规格化的球函数系数；R为地球半径；r为地面观测点到地球质心的距离；λ、θ为观测点的经度和纬度。

GARCE卫星数据观测得到的重力场球谐系数可以表示为重力场长期的静态平均值、重力场的长期变化与固体潮、海潮、极潮的影响及大气、非潮汐变化影响的组合。而对某个区域的某一时间跨度而言，重力场系数可以看成背景场与其改正之和[8]。

将GRACE卫星每年获得的重力场与背景重力场求差，就可得到年重力场的变化值：

即

其中，ΔC、ΔS 表示月重力场和背景重力场模型的球谐系数之差。为抑制GRACE卫星重力模型球谐系数高阶部分的噪声及截断误差的影响，加入各项同性高斯平滑函数Wl即

2 数值模拟地壳旋转位移引起的重力场变化

进行数据模拟的单个长方体参数为：X轴方向（X1=0 km，X2=20 km），Y轴方向（Y1=0 km， Y2=20 km），Z轴方向（Z1=0 km, Z2=30 km）。计算点分布在ζ=0．0的平面上，共100个，点间隔10 km，运动前后介质密度ρ=2.67×103kg/m3。表1为长方体旋转参数表。

表1 长方体旋转参数表

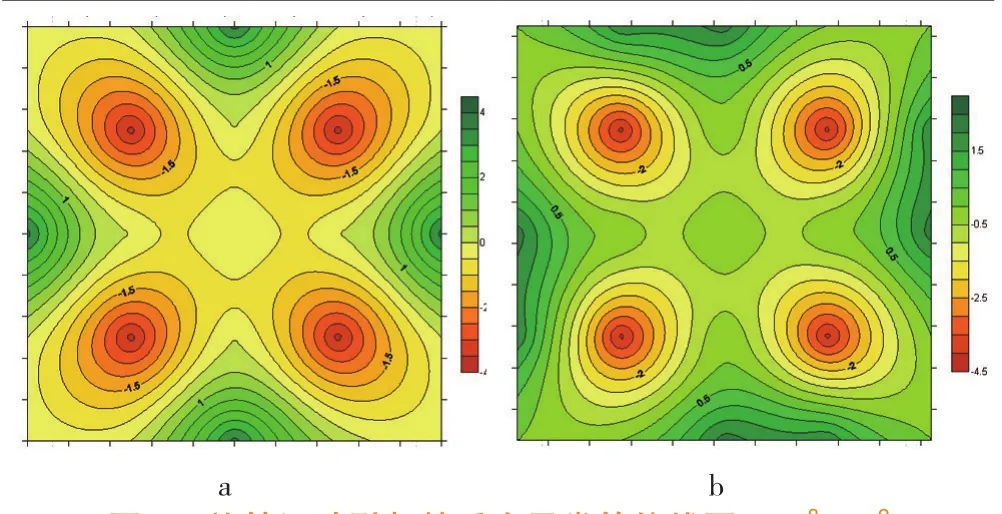
图1 旋转运动引起的重力异常等值线图/10-8ms-2

3 青藏高原地区重力场变化

图2中红色线框范围为本文研究区域。中国西部地区地壳运动的位移场整体上具有由西南向北东方向运动的特点，而且青藏高原地区绕喜马拉雅东构造具有明显的顺时针转动模式。

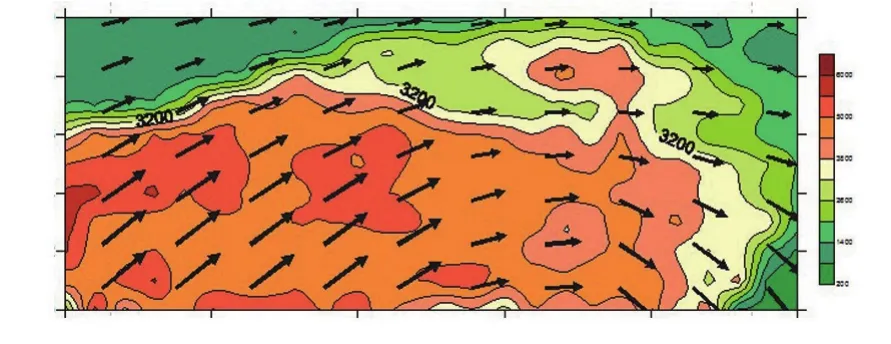
图2 青藏高原地区GPS运动速度场

3.1 GRACE卫星监测青藏高原地区重力变化

受时间和空间分辨率的影响，GRACE卫星在研究局部地区的重力变化及其原因上，效果不显著。但是可以从大尺度上反映地球重力场的变化。又考虑到间隔时间长的旋转运动应更明显，根据式（6）和式（8），以青藏高原地区东经80°～105°、北纬20°～35°地区GRACE GX-OG-_2-GSM 2005年12个月的重力场模型平均值作为背景重力场模型，与2009年12个月的重力场模型的平均值求差，计算2009年相对于2005年青藏高原地区的重力变化。模型最大阶次为120阶，高斯平滑半径取390 km，分辨率为1°×1°[10]，如图3所示。

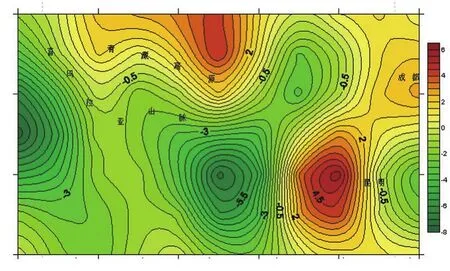
图3 2005～2009年青藏高原地区120阶重力场变化/10-8ms-2

从图中我们可以看到昆明以西地区是重力场变化值最大的地方，变化值为正值；而在喜马拉雅山脉的南部以及青藏高原地区和川滇区域的交界部分，重力异常值为负值。

将上述结果与该地区的GPS观测速度场（见图2）进行对比分析可以发现，因为青藏高原主体地壳向北运动,而且呈现由南到北逐渐减小的趋势，物质的流出较为明显, 所以该地区的重力变化值为负；而青藏高原地壳存在绕喜马拉雅东构造顺时针旋转运动，受到四川地块的阻挡作用，所以昆明以西地区的重力变化值为正[11]。

3.2 青藏高原地区数值模拟的重力变化

为方便计算，本文只考虑块体作旋转运动的情况，建立如图4所示坐标系，把图2所示研究区域分成15行25列，1°×1°大小的长方体。计算面为xoy平面（Z=0），即每个计算点都位于相应长方体在xoy平面投影的中心位置。对于每个长方体块体，地壳厚度统一取30 km，h表示块体地形高度，hmax表示块体地形的最大高度。

图4 块体地形高度

考虑到该地区的地形、气候等条件的影响，从http://www．ngdc．noaa．gov/网站获取青藏高原研究地区的地形数据，结合图3中红色线框所示范围内GPS观测站的运动速率[9]及《中国大陆现今地壳运动》附录二中记录的中国大陆GPS测站的速度场来确定块体运动[12]。对于GPS观测点分布不均匀的块体，采用以计算点为中心，以1°为半径搜索，按距离平方的倒数定权的方法进行加权平均内插得到。块体的旋转运动量为块体内所有旋转运动量的平均值，由公式（3）和（4）可得青藏高原地区重力变化如图5。

将旋转数据计算的重力变化与应用GRACE卫星数据计算的重力变化进行综合对比分析可知，两者的图形形态和数值都有较好的一致性。青藏高原地区的重力变化为负，昆明以西地区的重力变化值为正。但在部分地区也存在差异，这些差异需进一步研究。

图5 由旋转运动引起的青藏高原地区重力变化/10-8ms-2

[1] Trung N N,Lee S M,Que B C．Satellite gravity Anomalies and Their Correlation with the Major Tectonic Features in the South China Sea [J]． Gortdwand Research,2004,7(2):407-424

[2] Han S,Shum C,Bevis M,etal．Crustal Dilatation Observed by GRACE after the 2004 Sumatra-Andam an Earthquake[J]．Science,2006,313(5 787):658-662

[3] 周旭华,许厚泽,吴斌,等．用GRACE卫星跟踪数据反演地球重力场[J]．地球物理学报,2006,49(3):718-723

[4] 郑伟,许厚泽,钟敏,等．国际重力卫星研究进展和我国将来卫星重力测量计划[J]．测绘科学,2010,35(1):5-9

[5] 段虎荣,张永志,徐海军,等．中国西部地壳垂直运动引起的重力场空间变化特征[J]．大地测量与地球动力学, 2011,31(3):25-28

[6] 段虎荣,张永志,徐海军,等．中国西部地壳水平运动引起的重力场空间变化特征[J]．大地测量与地球动力学,2011,31(1):24-28

[7] 宁津生．卫星重力探测技术与地球重力场研究[J]．大地测量与地球动力学,2002,22(1):1-5

[8] 李立功．基于旋转模型的青藏高原重力变化研究[D]．西安:长安大学,2011

[9] 王琪,张培震,马宗晋．中国大陆现今构造变形GPS观测数据与速度场[J]．地学前沿,2002,9(2):415-429

[10] 段虎荣,张永志,刘锋,等．利用卫星重力数据研究中国及邻域地壳厚度[J]．地球物理学进展，2010,25(2):494-499

[11] 曹建玲,石耀霖,张怀,等．青藏高原GPS位移绕喜马拉雅东构造结顺时针旋转成因的数值模拟[J]．科学通报,2009,54(2):224-234

[12] 赖锡安,黄立人,徐菊生．中国大陆现今地壳运动[M]．北京:地震出版社,2004

P223.0