改进的SIFT双向匹配算法在异源影像匹配中的应用

梁建国，马 红

（1.重庆市勘测院，重庆 400020）

L（x，y，σ）= G（x，y，σ）* I（x，y） ( 1 )

改进的SIFT双向匹配算法在异源影像匹配中的应用

梁建国1，马 红1

（1.重庆市勘测院，重庆 400020）

针对不同传感器、不同时相、不同分辨率的异源遥感影像匹配困难的问题，引入尺度不变特征（Scale Invariant Feature Transform，SIFT）算法；针对传统SIFT匹配算法的不足，利用SIFT特征向量匹配对的唯一性约束改进传统SIFT算法的匹配策略，采用双向匹配以达到在匹配过程中准确寻找匹配点对的目的，提高影像匹配的正确率，实验证明，该方法适用于异源影像匹配。

SIFT特征匹配；双向匹配；异源影像匹配

目前主要的影像匹配可以分为3类：以灰度为基础的算法、以特征为基础的算法、以语义为基础的算法[1,2]。对于异源影像，由于数据量大、成像条件和场景条件复杂，基于灰度信息的匹配方法很难有效地解决特征对应问题，而基于语义信息的匹配算法依赖领域太大，还没有明显的研究进展[3]。由Lowe提出并完善的SIFT算法，能较好地抗影像尺度变换、旋转变换和亮度变换，在异源影像匹配中应用前景较为广阔[4,5]。然而单纯的SIFT算子用于异源影像匹配，存在匹配正确率低、匹配点数量较少且分布不均匀的情况。针对SIFT算子的不足，本文利用一种改进的SIFT双向匹配算法，即在已有匹配结果的基础上引入匹配的唯一性约束，提高两幅待匹配影像之间的匹配正确率[6]，实现光谱特征、空间特征和纹理特征都有差异的异源影像匹配。

1 SIFT特征向量的提取

SIFT特征匹配算法包括特征向量提取和特征向量匹配2步。特征向量提取包括如下几个步骤：尺度空间极值点检测、特征点定位、特征点方向确定、特征向量生成[7]。

1.1 尺度空间极值点检测

高斯卷积核是实现尺度变换的唯一变换核，故图像I（x，y）的尺度空间L（x，y，σ），定义为原始图像与一个可变尺度的二维高斯函数G（x，y，σ）的卷积运算：

L（x，y，σ）= G（x，y，σ）* I（x，y） ( 1 )

不变尺度的二维高斯函数为：

将一系列尺度空间图像中的相邻尺度相减就得到一组DOG（Difference Of Gaussian，即高斯差分算子）图像D（x，y，σ）：

将当前被检测的像素与同一尺度上的相邻8个像素以及邻近的高低2个尺度上对应位置的9×2个像素进行比较，确保在尺度空间和二维图像空间都检测到局部极值，完成尺度空间检测。

1.2 确定特征点位置

根据极值点在位置和尺度上用2×2 的Hessian矩阵H计算其稳定性，用稳定性度量标准η剔除不稳定的点，从而找出稳定的特征点。H矩阵和η如下：

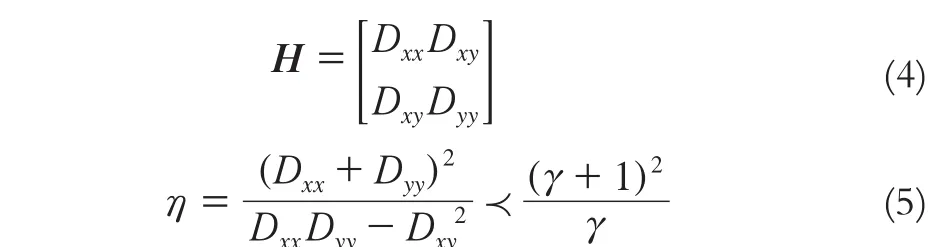
式中，γ是控制特征点稳定性的参数，表示为最大特征值和最小特征值的比值。

1.3 确定特征点方向

利用高斯卷积图像确定特征点的唯一指向，保证特征向量满足旋转不变性，计算其梯度幅值m和方向θ，如式（6）和式（7）所示。在计算过程中，以特征点为中心的邻域梯度直方图的峰值表示特征点的方向。

1.4 生成特征向量

将特征点的16×16邻域分为4×4的图像子块，每个像素定义8个方向的向量信息，即可生成 128维的特征向量。由此，每个SIFT特征点由1个128维向量表示，SIFT特征向量已经除去了尺度变化、旋转变换等因素的影响，如果将其进行归一化处理，则可进一步减少光照变化的影响[8,9]。

2 特征向量匹配策略的改进

SIFT特征向量的匹配采用最邻近距离算法完成，即采用样本特征点的最邻近特征点欧氏距离与次邻近特征点欧氏距离的比值是否满足设定的匹配阈值来完成[9,10]。这种在参考图像中寻找待匹配图像特征点对应点的方式是带有方向性的，即为待匹配图像到参考图像的单向匹配，匹配方法简便，但误匹配概率较大。在异源影像匹配过程中，特征匹配的正确率直接影响匹配结果，对后续利用的限制较大，因此，需要对传统SIFT单向匹配算法进行改正，以提高异源影像匹配的正确率。

唯一性约束，即匹配点对之间映射关系的对称性，对于匹配点（p1，p2），存在匹配映射关系（p1→p2）和（p2→p1）。将唯一性约束引入到匹配策略中，实现SIFT特征向量的双向匹配，可以减少误匹配点，进而提高匹配的正确率。

本文改进的SIFT特征向量双向匹配的步骤如下（见图1）：

①采用单向匹配中提取特征向量的方法提取2幅图像各自的SIFT特征向量；

②根据传统SIFT特征向量的匹配算法，计算第1个特征点集m到第2个特征点集n中的匹配对；

③根据计算得到的匹配点对集合，用同样的方式反过来计算第2个特征点集n中已经被匹配的关键点在第1个特征点集m中的匹配点，即求已被匹配的关键点在第1个特征点集m中的最邻近与次邻近的距离比率，若比率小于匹配阈值b，则作为正确匹配点[7]。

a、b为匹配阈值，在实验过程中a、b不相互影响，可设置为相同值。

改进后双向匹配算法约束条件比传统SIFT算法约束条件更强，可以检测出更多的误匹配点，从而提高匹配的正确性。

图1 SIFT特征向量双向匹配流程

3 匹配实验及结果分析

本文实验环境如下：CPU为Intel(R) Core(TM) i5-3570 3．40 GHz(4 CPUs) ～3．8 GHz；内存为4 GB；操作系统为Windows 7；实验平台为Microsoft Visual Studio 2010和Opencv 2．4．0。

本文选用不同传感器获取的同一地区不同时相影像进行匹配，以验证改进的SIFT算子匹配效果。实验数据为图2中的影像，a图为2010年9月获取的重庆市江北区SPOT 5卫星影像（分辨率为10 m，影像质量较差，噪声较多），b图为2011年4月获取的重庆市江北区QuickBird卫星影像（分辨率为2．44 m，影像质量较好，噪声较少），在实验前将QuickBird影像进行逆时针旋转15°，以验证匹配算法的几何变换不变性。

图2 重庆市江北区实验卫星影像

针对2幅实验影像，分别采用传统的SIFT算法和本文改进后的双向SIFT算法进行匹配，实验结果如图3所示。

表1在特征点匹配的正确率和所用时间上将2种方法进行了比较：①在匹配正确率方面，改进的SIFT双向匹配算法匹配正确率明显高于传统SIFT匹配算法；②在计算时间方面，改进的SIFT双向匹配算法由于在传统匹配的基础上进行了反向匹配，时间效率比传统SIFT算法低。

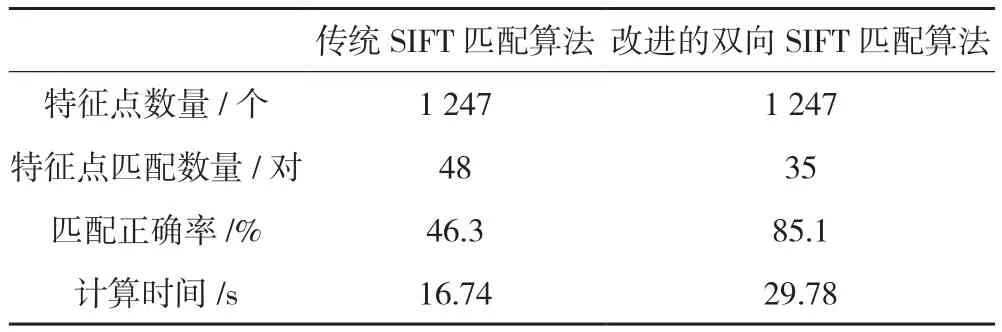
表1 异源影像匹配结果比较

图3 实验结果

4 结 语

改进的SIFT双向匹配算法在影像后续处理中可以得到广泛引用，如目标识别和目标跟踪等。由于双向匹配策略造成匹配耗时较长，且在计算过程中，匹配阈值a和b对结果的影响没有排除，在下一步工作中，将采用分块处理方式完成匹配，并采用自适应方法设定匹配阈值。

[1] 翟丽杰．基于特征点的改进SIFT岩心图像匹配算法[J]．计算机与数字工程,2013,41(6): 981-983

[2] 袁修孝,李然．带匹配支持度的多源遥感影像SIFT匹配方法[J]．武汉大学学报:信息科学版,2012,37(12): 1 438-1 442

[3] 柯涛,张永军．SIFT特征算子在低空遥感影像全自动匹配中的应用[J]．测绘科学,2009,34(4):23-26

[4] 李然,张云生．基于SIFT特征的多源遥感影像自动匹配方法[J]．测绘科学,2011,36(3):8-10

[5] DGL．Distinctive Image Features from Scale-Invariant Key Points[J]．Int，J Comput Vision，2004,60(2): 91-110

[6] 刘焕敏．一种改进的SIFT双向匹配算法[J]．兵工自动化,2009,28(6):89-91

[7] 吕倩利,邵永社．基于SIFT特征的异源遥感影像匹配方法研究[J]．计算机工程与应用，2012,48(36): 171-175

[8] 张春美,龚志辉,孙雷．改进SIFT特征描述符在影像匹配中的应用研究[J]．计算机工程与应用,2008,44(2): 95-97

[9] 唐永鹤,卢焕章．基于多结构元素复合滤波的形态学边缘检测[J]．武汉大学学报:信息科学版,2012,37(1): 50-53

[10] 赵垒,侯振杰．一种改进的SIFT图像配准方法[J]．计算机工程,2010,36(12):226-228

P237.3

B

1672-4623（2014）06-0057-02

10.3969/j.issn.1672-4623.2014.06.020

梁建国，正高职高级工程师，现主要从事遥感应用研究、三维仿真地理信息系统与网络底图应用开发。

2014-01-23。

项目来源：国家科技支撑计划资助项目（2011BAH12B07-03)。