IGS精密卫星钟差插值算法的精度比较与分析
2014-04-18杨勇喜何秀凤王俊杰
杨勇喜, 何秀凤, 王俊杰
(1.河海大学 卫星及空间信息应用研究所,江苏 南京210098)
IGS精密卫星钟差插值算法的精度比较与分析
杨勇喜1, 何秀凤1, 王俊杰1
(1.河海大学 卫星及空间信息应用研究所,江苏 南京210098)

采用IGS提供的30 s、5 min和15 min间隔的精密卫星钟差产品,比较、分析了线性插值、拉格朗日插值、三次样条插值和两点三次埃尔米特插值等精密卫星钟差插值算法的精度。结果表明,线性插值精度最高,其余算法精度相当。拉格朗日插值存在奇偶性质,奇数阶插值比相邻偶数阶精度高,插值精度随阶数的增加有降低的趋势。钟差插值精度与卫星本身的钟差抖动程度有关,钟差抖动越大,精度越低。使用间隔较小的钟差产品插值精度更高。
IGS;精密卫星钟差;线性插值;拉格朗日插值;钟差抖动
IGS提供的精密钟差产品广泛应用于卫星定轨[1-3]、精密单点定位[4,5]等领域。高采样率的精密钟差有助于提高精密定轨的精度[2],显著改善精密单点定位精度、加快收敛速度[5]。但是,现阶段IGS仅提供30 s、5 min 和15 min的最终钟差产品,对于30 s以内的静态定位和高频动态定位(1 Hz以上)必须通过内插得到对应历元的卫星钟差,常用的插值算法有线性插值、拉格朗日插值、样条插值和埃尔米特插值等。张丽、杨乐、张清华、吴继忠和任锴等认为线性插值精度最高[6-10],王俊、曹凤志等认为两点三次埃尔米特插值精度最高[11,12],郭东美认为样条插值最为优异[13],洪樱认为线性插值与多项式插值的差距并不大[14],雷雨建议首选拉格朗日插值方法[15]。
为比较、分析精密钟差的插值精度,本文选取3 个钟差变化较为典型的卫星,采用IGS提供的30 s、5 min和15 min最终钟差产品,分别用线性插值、拉格朗日插值、三次样条插值和两点三次埃尔米特插值等算法进行钟差插值,得出了一些有益的结论。
1 精密卫星钟差插值算法
1.1 线性插值
假定给定区间[xk,xk+1]及其端点函数值yk=f(xk),yk+1=f(xk+1),要求线性插值多项式L(x),使它满足L(xk)=yk,L(xk+1)=yk+1其几何意义就是通过(xk,yk)与(xk+1,yk+1)的直线。满足上述条件的线性插值多项式为:

1.2 拉格朗日插值
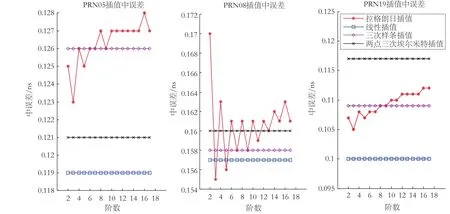
已知n+1个节点 [x0, y0],[x1, y1],[x2, y2],…,[xn, yn](x0 则满足式(2)的插值多项式可以表示为:即拉格朗日插值多项式。但由拉格朗日插值多项式的余项可知,截断误差在靠近2端已知点的位置很不稳定[16]。为得到较高精度的插值结果,可以采用滑动区间的拉格朗日插值算法进行钟差插值[14]。如果已知点为偶数个,则保证2端各有一半的已知点。如果已知点为奇数个,则让右(左)比左(右)边多一个。 1.3 三次样条插值 若函数S(x)∈C2[a,b],且在每个小区间[xj,xj+1]上是三次多项式,其中a = x0 则称S(x)为三次样条插值函数。 1.4 两点三次埃尔米特插值 IGS提供的5 min间隔精密卫星钟差产品同时包含钟差和钟速,因此可以通过埃尔米特插值算法内插得到30 s的卫星钟差[12]。其常见的形式是两点三次埃尔米特插值多项式,插值节点取xk,xk+1,插值多项式H3(x)满足条件:两点三次埃尔米特插值多项式H3(x)的计算公式为: 采用IGS提供的2013-09-25(GPSWeek1759)的15 min、5 min、30 s的最终卫星钟差产品进行分析。通过比较全天GPS 15 min间隔精密钟差变化,选取PRN05、PRN08和PRN19三颗变化较典型的卫星,其钟差变化如图1。由图可知,PRN05、PRN19卫星的钟差变化较平缓,而PRN08卫星钟差有较大抖动。 图1 PRN05、PRN08和PRN19精密卫星钟差变化 采用上述插值算法,由15 min间隔的卫星精密钟差插值得到5 min间隔的卫星钟差(15~5 min),与IGS 5 min精密钟差对比,结果见表1。3颗卫星精密钟差插值误差的中误差见图2(线性插值、三次样条插值和两点三次埃尔米特插值没有阶数的变化,为便于比较,与拉格朗日插值绘制在同一张图,表现为直线)。由5 min间隔的卫星精密钟差插值得到30 s间隔的卫星钟差(5 min~30 s),与IGS 30 s精密钟差对比,结果见表2。3颗卫星精密钟差插值误差的中误差见图3。 表1 15 min精密钟差内插5 min钟差与IGS 5 min精密钟差对比/ ns 图2 PRN05、PRN08和PRN19 15 ~5 min插值中误差 图3 PRN05、PRN08和PRN19 5 min~30 s 插值中误差 表2 5 min精密钟差内插30 s钟差与IGS 30 s精密钟差对比结果/ ns 由表1可知, PRN05、PRN19两颗卫星各种插值算法的误差绝对值分别小于0.5 ns、0.7 ns,中误差均小于0.16 ns,中误差的差异小于0.02 ns(等价距离6 mm);PRN08卫星各种插值算法的误差绝对值小于1.2 ns,中误差小于0.45 ns,中误差的差异小于0.06 ns。因此15~5 min钟差抖动越大,插值误差越大(可达ns级),对应的中误差越大,各种插值算法的差异也越大。 由图2可知,15~5 min线性插值精度最高。对于PRN05,拉格朗日插值比三次样条插值精度高。对于PRN08、PRN19,低于一定的阶数,拉格朗日插值比三次样条精度高。对比3颗卫星插值误差最大值、最小值变化图(篇幅限制,未给出),拉格朗日插值表现出奇偶特性。如图2中的PRN05卫星钟差,奇数阶插值比相邻偶数阶插值精度高。随着拉格朗日插值阶数的增加,精度有降低的趋势。 由表2可知,5 min~30 s各种插值算法的误差绝对值比较接近,均小于0.7 ns,中误差均小于0.2 ns,中误差的差异均小于0.02 ns(等效距离6 mm)。因此,5 min~30 s各种插值算法的精度比15~5 min高,且插值算法间的差异更小。 由图3可知,5 min~30 s线性插值最佳。三次样条插值比一定阶数的拉格朗日插值精度高;拉格朗日插值呈现出明显的奇偶特性,且随着阶数的增加,精度有下降的趋势。两点三次埃尔米特插值与其他插值算法对比,在精度方面没有明显优势,且表现出很大的不稳定性。 本文利用IGS提供的30 s、5 min和15 min间隔的最终精密钟差产品,比较、分析了不同插值算法的精度,得出以下结论。 1)15~5 min、5 min~30 s线性插值精度最高,且算法简单、计算效率高。在GNSS后处理过程中,建议采用线性插值算法得到特定历元的精密卫星钟差。 2)拉格朗日插值、三次样条插值和两点三次埃尔米特插值精度相当。拉格朗日插值算法存在奇偶性质,奇数阶插值比相邻偶数阶精度高,插值精度随着阶数的增加有降低的趋势;两点三次埃尔米特插值虽然考虑了卫星钟速,但是插值效果比线性插值精度要低。 3)钟差插值精度与卫星本身的钟差抖动程度有关,钟差抖动越大,插值误差越大,精度越低。15~5 min插值误差最大可达ns级,5 min~30 s插值最大误差为亚ns级。 4)5 min~30 s插值精度相对于15~5 min插值精度高,各种插值算法精度差异小。因此,钟差插值时建议使用高采样率的钟差产品(如30 s钟差产品)。 [1] 韩保民. 精密卫星钟差加密方法及其对星载GPS低轨卫星定轨精度影响[J].武汉大学学报:信息科学版,2006 (12):1 075-1 078 [2] 张守建,李建成,邹贤才,等. GRACE卫星非差运动学精密定轨分析[J].武汉大学学报:信息科学版,2010 (6):679-682 [3] 郑作亚,党亚民, 阳凡林,等.星载GPS相位非差运动学定轨中误差影响分析[J].大地测量与地球动力学,2010 (6):66-70 [4] 徐爱功,徐宗秋,隋心.卫星轨道与钟差对精密单点定位精度的影响[J]. 测绘通报,2013 (5):1-4 [5] 张小红,郭斐,李星星. IGS卫星钟差产品采样间隔对PPP精度的影响[J].武汉大学学报:信息科学版,2010 (2):152-155 [6] 张丽,徐源强,李政. 精密单点定位中卫星钟差插值方法研究[J].测绘通报,2013 (7):16-18 [7] 杨乐,张书毕,侯东阳,等.四种精密卫星钟差插值方法的比较[J].测绘信息与工程,2011 (3):8-10 [8] 张清华,隋立芬,牟忠凯.几种精密卫星钟差加密方法的比较与分析[J].测绘工程,2010 (2):65-67 [9] 吴继忠,高俊强,李明峰.IGS精密星历和钟差插值方法的研究[J].工程勘察,2009(7):52-54 [10] 任锴,杨力.精密卫星钟差两种插值方法的比较[J].测绘信息与工程,2009(6):5-6 [11] 王俊,方书山.精密卫星钟差内插的三种方法及精度分析[J].全球定位系统,2012(4):49-52 [12] 曹凤志,方书山. 精密卫星钟差内插的埃尔米特方法[J]. 全球定位系统,2011(6):22-24 [13] 郭东美,韩保民,熊熊.低轨卫星定轨中精密卫星钟差的插值方法[J].大地测量与地球动力学,2007(2):103-106 [14] 洪樱,欧吉坤,彭碧波.GPS卫星精密星历和钟差三种内插方法的比较[J].武汉大学学报:信息科学版,2006(6):516-518 [15] 雷雨, 赵丹宁. IGS 精密钟差文件的读取及加密方法[J]. 地理空间信息, 2013, 11(3): 32-33 [16] 李庆扬,王能超,易大义. 数值分析[M]. 北京:清华大学出版社,2009. P228.41 B 1672-4623(2014)06-0029-04 10.3969/j.issn.1672-4623.2014.06.011 杨勇喜,硕士,主要研究方向为卫星大地测量。 2013-12-23。 项目来源:国家自然科学基金资助项目(41274017、41204002、41301449);江苏省科技支撑计划资助项目(BE2010316);江苏省普通高校研究生科研创新计划资助项目(CXZZ11_0451)。




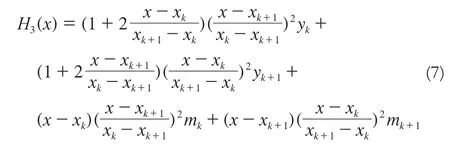
2 结果与分析




3 结 语
