汽车转向节拓扑优化方法研究及应用*

兰凤崇，张浩锴，王家豪，陈吉清

(1.华南理工大学机械与汽车工程学院，广州 510640;2.华南理工大学，广东省汽车工程重点实验室，广州 510640)

前言

转向节是汽车悬架系统的重要机件，它连接轮毂和悬架控制臂，同时是转向节臂与制动卡钳的安装载体，承受汽车前部载荷，支承并带动前轮绕主销转动而使汽车转向，确保汽车稳定行驶并灵敏传递行驶方向。在汽车行驶状态下，它承受着复杂多变的载荷工况。因此需要有较大的刚度和足够的强度与安全系数;同时还要尽可能减轻质量，以满足操纵稳定性和整车轻量化的要求。转向节的优化首先是一个结构优化问题，结构优化按设计变量和面向问题的不同可分为拓扑优化、形状优化和尺寸优化。针对转向节的结构特点，结构拓扑优化最适用于结构设计的初始阶段，用来提供参考意义很强的概念性的设计方案。与先设计再校核的传统设计方法不同，拓扑优化是由CAE驱动的设计思路。

当前大部分的拓扑优化均是以结构的某个性能指标最大化或最小化为目标函数进行的单目标优化，再对优化后的新结构进行分析以验证其他指标。由于不同指标之间具有不一致性，这种方法很难得到最优的结构。为了使结构在多个工况或多个性能指标同时达到最优，许多学者对结构的多目标拓扑优化问题进行了研究。文献［1］中采用带权重的折衷规划法进行车架的拓扑优化，实现了客车车架结构的多刚度拓扑优化。在实现轻量化的基础上满足各工况下的汽车动力学性能。本文中运用折衷规划法进行转向节的拓扑优化，收到了较好的效果。

1 转向节拓扑优化的数学模型

本文中以方程式赛车的右前轮转向节为研究对象，对其进行多目标拓扑优化，以寻求更优的结构方案，同时弥补原结构的一些不足:结构材料分布过于空旷导致的刚度不足与应力集中。为了可调整参数而设计的分体式卡钳支架和分体式的转向臂，增加了零件数量，导致成本和质量的增加。原右前轮转向节结构见图1。在相关设计参数确定的前提下，优化的设计方案将会把转向臂和卡钳与转向节主体整合。从轻量化考虑，该赛车转向节采用铝合金。

对转向节的优化是在尽量减轻质量的前提下，使其刚度和固有频率最大化，属于典型的以静力学中的刚度最大化和动力学中的特征值最大化作为优化的目标函数的多目标优化问题［2］。传统的多目标优化问题采用线性加权和法将多目标问题转化为单目标问题求解，如果所有的目标函数之间不存在冲突，那么使它们同时达到最优解很易求得。然而实际问题中这种情况很少，如果目标函数中至少有两个存在冲突(即非凸优化问题)，至少有一个目标函数的增加必然导致另一个目标函数的减少，所以对非凸优化问题来说，线性加权和法不能确保得到所有的Pareto最优解。折衷规划法(compromise programming approach)在多目标拓扑优化问题的研究中能较好地解决上述不足，因此经常被用于解决结构多目标优化的问题，其思想是把多目标优化问题的折衷解看作是与每一个目标函数的理想解距离最小的矢量［3］，因此折衷规划法的实质是把多目标问题更加合理地转化为单目标问题求解。实际上结构在不同工况和不同目标函数之间的数量级存在较大差异，故须将目标函数的折衷解与其理想解的绝对距离转化为相对距离，使它们之间能够相互进行比较。

1.1 多工况刚度拓扑优化模型

拓扑优化是研究在设计域内得到合理的材料分布，使结构刚度最大化的问题。在多工况下的刚度拓扑优化问题中，每一个不同的载荷工况将对应不同的最优拓扑结构［4］。因此，静态多工况拓扑优化问题本身也属于多目标拓扑优化问题，利用折衷规划法转化为单目标问题求解。

工程中通常把刚度最大问题等效为柔度(compliance)最小化问题来研究，柔度值为单元总应变能值，更加方便计算与提取［5］。由折衷规划法可得静态多刚度拓扑优化的目标函数为

式中:m为载荷工况总数;wk为第k个工况的权值;q为惩罚因子，且q≥2;Ck(ρ)为第k个工况的柔度目标函数;Cmaxk为第k个工况柔度的最大值，即由优化前原结构分析得到的应变能;Cmink为第k个工况柔度的最小值，即为填充材料后的模型进行分析得到的应变能;ρ为设计变量即材料密度;V(ρ)为优化后结构的有效体积;V0为结构的原始体积;f为体积约束的百分比。

1.2 动态固有频率拓扑优化模型

动态固有频率拓扑优化一般将几个低阶的重要频率的最大化作为目标函数。其中第1阶固有频率往往是结构整体刚度的重要指标，结构中存在薄弱环节将导致第1阶固有频率的降低。由于转向节对于各阶固有频率下的振型无特别的要求，故只以第1阶固有频率最大化为目标进行动态固有频率的拓扑优化。针对频率的动力特性，拓扑优化目标函数是在满足结构约束的情况下改善结构的模态特性，使结构整体刚度提高、材料得到优化配置。无阻尼自由振动模型的特征值可表示为

式中:K为结构的刚度矩阵;M为质量矩阵;λi和Ui为各阶特征值和特征向量;fi为固有频率。模态频率特征值优化的数学模型为式中:wi为第i阶特征值的加权系数。本文中只对第1阶频率进行优化，故i=1，wi=1。

1.3 考虑刚度和频率的多目标拓扑优化模型

结构多目标拓扑优化是以体积比作为约束，同时考虑静态多刚度目标和动态振动频率目标的拓扑优化［6］。由带权重的折衷规划法可得到多目标拓扑优化的综合目标函数为

式中:F(ρ)为综合目标函数;w为柔度目标函数的权重。为了消除不同量纲之间数量级的差别，引入了Λmin和Λmax，Λmin为频率目标函数的最小值，由优化前的结构分析得到的固有频率;Λmax为频率目标函数的最大值，由填充材料后的模型进行分析得到的固有频率，同时将频率最大化的问题变换为函数的最小化问题来求解。

2 转向节的拓扑优化

采用Altair HyperWorks中的 Optistruct模块进行优化求解，Optistruct软件利用带惩罚的变密度法(SIMP)插值方法作为材料模型，用凸规划法中的移动渐进线法作为优化算法，同时采用下限约束法和周长约束法控制数值不稳定现象。

2.1 转向节的拓扑优化流程

转向节的多目标拓扑优化流程如图2所示。

2.2 有限元模型与边界条件的建立

在Hypermesh中对原结构进行设计区域填充，同时预留其他零件安装所需空间，建立转向节的有限元模型，作为拓扑优化的基础结构，见图3。图中浅色单元为拓扑优化区域。材料为铝合金，弹性模量为69 000MPa，泊松比为 0.33，密度为2 700kg/m3，体积分数约束为0.25，并考虑加工因素指定拔模方向为中心孔轴线方向。

基于赛车道路路况下对整车在制动、转向和车轮跳动等典型工况进行多体动力学分析，获得转向节连接上下控制臂的球销点、转向节臂球销点与制动卡钳作用点的受力情况，以此作为转向节静态分析的载荷边界条件，见表1。载荷通过RBE2刚性连接单元作用在转向节各支架上。此外，须在Control Card中设置MODETRAK卡片，以避免在模态优化过程中出现模态振荡的现象。

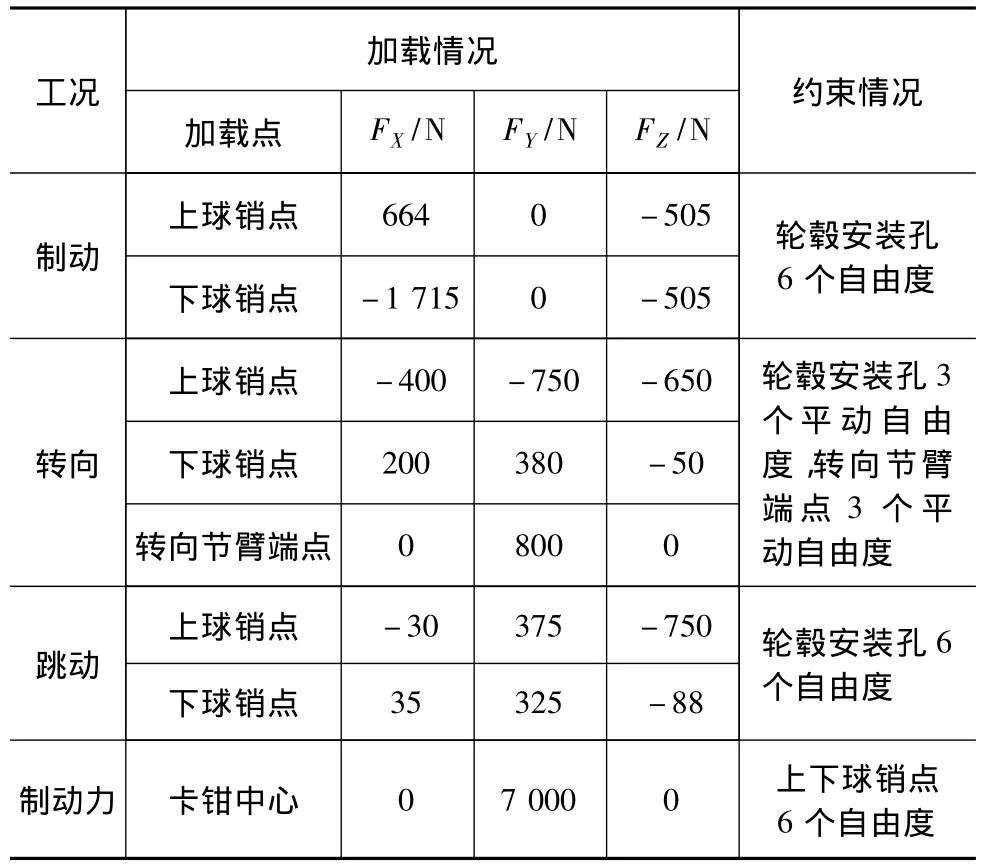
表1 右前转向节的载荷工况

目前在OptiStruct中不能直接进行真正意义上的多目标拓扑优化，实现多目标优化有多种处理方法，例如把多个优化目标中的一个作为目标函数，其余的目标作为约束条件。针对本问题较为理想的方法是利用OptiStruct中提供的自定义函数功能来定义所提到的折衷规划公式(4)，然后把定义的函数设为响应，最后把该响应作为拓扑优化的目标函数。

2.3 优化结果

计算经过56次迭代后结束，优化的拓扑结构如图4所示，各目标函数的优化迭代过程如图5和图6所示。可以看出，经过多目标拓扑优化后结构的载荷路径较清晰，并生成原转向节没有的肋板状结构，这些肋板是结构刚度得到提升的重要因素。由于设定了拔模方向，使结构优化的结果在生产工艺上基本可行。另外由于结构的拓扑优化仅仅考虑了结构本身的最优，无法把加工制造的成本加入考虑，所以使优化结果相比优化前显得不规整，有可能导致加工难度与加工成本上升，所以在详细设计中须对其进行适当的修正。由迭代曲线可知，迭代中不同工况下柔度目标函数有着相同的波动趋势，相对原结构柔度均有不同程度的下降，而柔度变小(刚度变大)的同时1阶固有频率也升高，可以看出柔度和频率是相互制约的。

图5和图6表明优化后各指标均有所提升，然而拓扑优化结果只是一种概念性的材料分布图形，其结果并不能准确地代表真实结构的性能，但可以为结构的设计提供参考，只有将其转化为具体的结构方案再讨论其性能才有意义。

2.4 方案设计与验证

优化结果可通过Optistruct的OSSmooth模块输出igs格式的几何模型，作为几何建模的参照物。转向节的新方案设计需要结合实际加工工艺和其他因素，在CATIA中进行设计。

转向节的新方案设计分为概念设计和局部优化两个阶段。概念设计是参照拓扑优化结果进行的结构材料分布的初步设计，对结构的性能有重要的影响;局部优化是在概念设计的基础上再对局部进行形状优化，以消除局部的刚度不足或应力集中的情况。本文中只针对体现拓扑优化结果的概念设计方案进行分析讨论。

本例中转向节采用CNC数控加工工艺，建模过程在考虑加工刀具的可达空间和工件的装夹等因素的基础上，比较忠实地还原了拓扑优化结果的细节特征，如图7所示。优化后的拓扑结构在细节上比较粗糙，为了使其结构比较规整而便于制造，初步设计主要通过直边与倒圆角组合的方式来贴近优化后拓扑结构的几何图形的边缘，而局部的肋板细节则通过建立与其厚度相近的等厚肋板来实现，从而建立新方案的参数化几何模型。建立优化后设计方案的有限元模型，通过表1的载荷工况再对其进行分析验证，其结构的各方面性能指标均有显著提升，同时质量有所减轻，达到了设计目的，见表2。

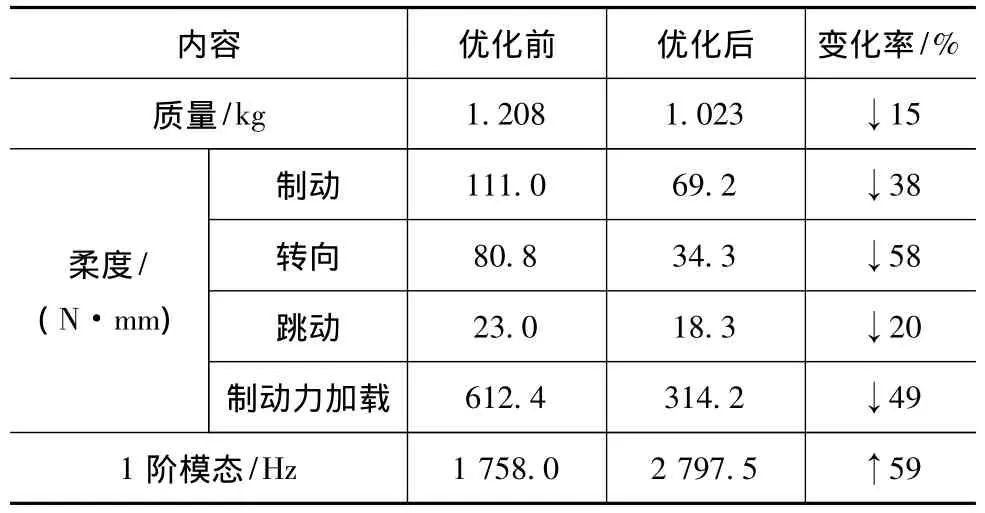
表2 优化前后的性能对比

对新转向节的概念设计方案进行强度校核发现，最大应力值为95.2MPa，出现在制动力作用下的卡钳安装支架处，见图8。相比于优化前150MPa的最大应力值有显著下降。转向节所采用2024铝合金的屈服强度超过245MPa，安全系数接近3，满足使用要求，所以新的结构方案强度也优于原结构。

3 结论

(1)运用带权重的折衷规划法建立了转向节以多工况下的静态刚度和1阶固有频率最大化为目标函数的综合优化模型，进行拓扑优化设计。根据优化的结果，结合实际工艺设计出转向节新结构概念方案并进行了验证与校核。

(2)以方程式赛车的转向节为实例，运用该方法进行转向节的多目标拓扑优化。结果表明，优化后方案在轻量化基础上使多工况下柔度显著减轻，动态1阶固有频率显著增大，达到了多目标优化目的。同时表明，运用折衷规划法的多目标拓扑优化设计方法进行转向节优化设计是可行且有效的。

［1］ 范文杰，范子杰，桂良进．多工况下客车车架结构多刚度拓扑优化设计研究［J］．汽车工程，2008，30(6):531 －533．

［2］ Chen T Y，Wu S C．Multi Objective Optimal Topology Design of Structures［J］．Computational Mechanics，1998，21(6)．

［3］ 刘林华，辛勇，汪伟．基于折衷规划的车架结构多目标拓扑优化设计［J］．机械科学与技术，2011，30(3):382 －385．

［4］ 祝小元，方宗德，申闪闪，等．汽车悬架控制臂的多目标拓扑优化［J］．汽车工程，2011，33(2):138 －141．

［5］ 沈安林，肖守讷．车体结构多目标拓扑优化设计探讨［J］．铁道机车车辆，2011，31(3):5 －7．

［6］ Min S，Nishiwaki S，Kikuchi N．Unified Topology Design of Static and Vibrating Structures Using Multiobjective 0ptimization［J］．Computers and Structures，2000，75:93 －116．