PWM整流器数学建模及参数整定方法

王颖

（天津经济技术开发区汉沽现代产业区总公司，汉沽 300480）

有源前端AFE（active front end），在工程领域应用较广，学术研究中多采用脉宽调制PWM（pulse width modulation）整流器这一名称。和传统的二极管整流相比，AFE具有功率因数可控、网侧电流正弦度好、能量可双向流动、直流侧电压稳定、动态响应快等诸多优点，其应用日益广泛[1～4]。

对AFE的研究最早开始于20世纪80年代，自关断器件的日趋成熟推动了PWM技术在变流器上的应用及相关研究[5～6]。目前，针对AFE的研究主要包括数学建模与分析、主电路拓扑、系统控制策略研究等方面，其中数学建模和分析一直是AFE研究的热点问题。文献[7～8]在三相静止参考坐标系下建立了AFE的数学模型，并说明了其电流控制的原理；文献[9]针对AFE的稳态直流模型、低频小信号交流模型及高频模型做了全面分析，虽然分析过程完整、详细，但过于复杂，实际应用较为困难。

本文介绍了一种AFE系统建模方法[10]，该方法考虑了AFE的开关函数，对电压、电流变量做采样周期内的平均值处理，得出了AFE在dq旋转坐标系下的平均值数学模型。基于上述模型，本文进一步研究了AFE的电流解耦控制方法，采用等效传函方法设计了电流环、电压环控制器参数，并进行了仿真验证。仿真结果表明，模型的电流控制实现了有功、无功电流分量的解耦，辅以合理设计的控制器参数，AFE系统具有良好的动、静态性能。

1 AFE系统数学模型

1.1 系统结构及静止坐标系方程

AFE整流器系统的拓扑结构如图1所示。图中，uga、ugb、ugc分别为电网相电压，ua、ub、uc分别为AFE输入端相电压，ia、ib、ic分别为AFE的输入三相电流，udc、idc分别为AFE直流侧电压、电流，L、R分别为AFE输入侧滤波电感及线路等效电阻，C为直流电容，iL、ZL分别为负载电流及等效负载阻抗。

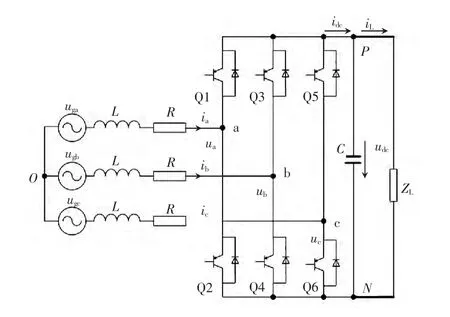
图1 AFE系统结构Fig.1 Structure of AFE system

为简化分析，通常对图1系统做如下假设：①电网电压理想，为标准三相正弦；②滤波电感L线性，不考虑饱和；③功率开关等效为理想开关。

根据上述假设，可得

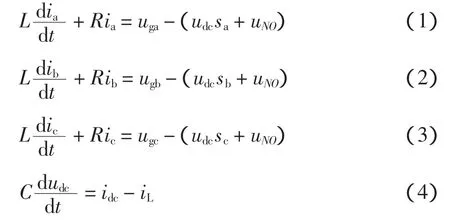
式中，sa、sb、sc分别为AFE三相桥臂的开关函数，功率器件开通时为1，关断时为0。则式（4）可改写为

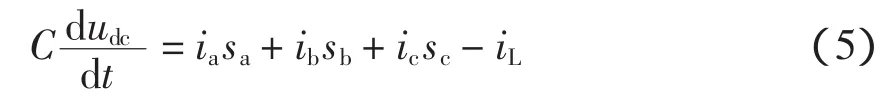
由于三相对称，电网电压、电流应满足

联立式（1）～式（6），得

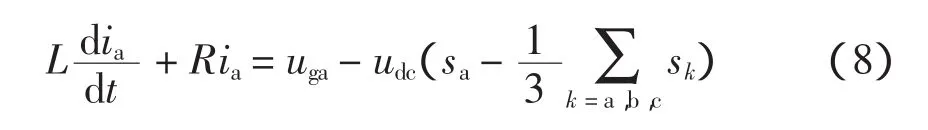
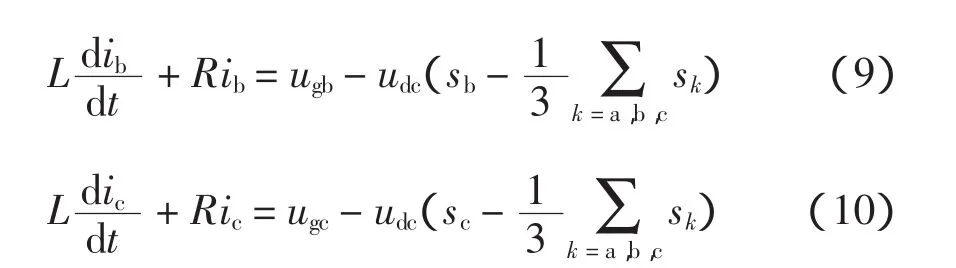
式（5）、式（8）～（10）描述了AFE交、直流侧的电压、电流关系，构成了AFE在静止坐标系下的数学模型。

1.2 旋转坐标系数学模型

静止坐标系下的数学模型，其电压、电流均为正弦量，控制系统设计较为复杂。采用等幅值旋转坐标变换将式（5）、式（8）～（10）变换至旋转坐标系dq，表达式为

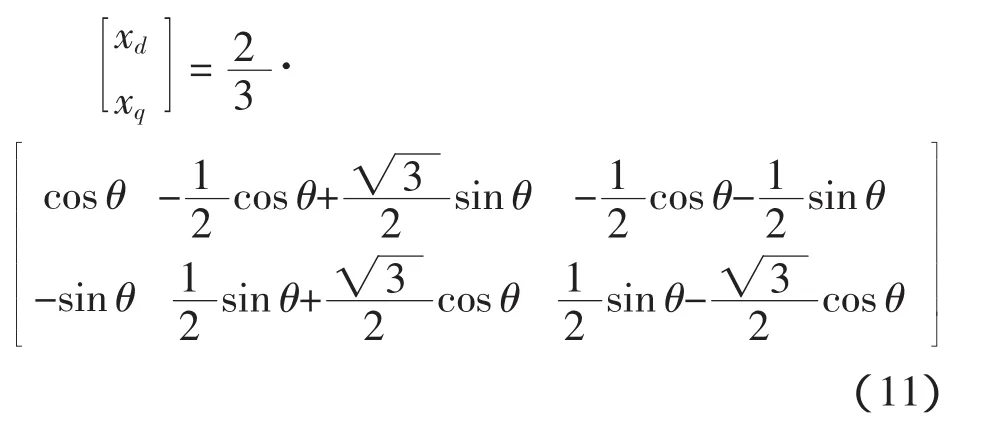
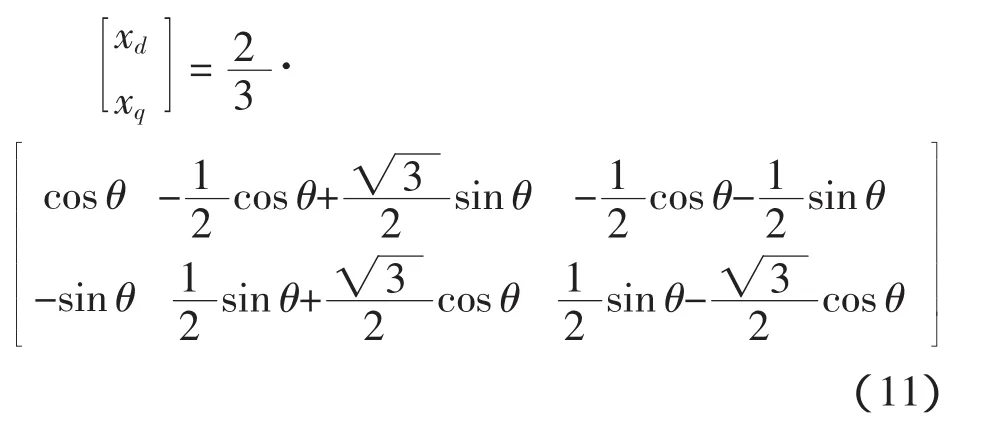
式中，θ为d轴超前于a相的角度。如果选取d轴和电网电压矢量ug同向，则θ通常由软件锁相环计算获得[11]。

旋转变换后的AFE数学模型为

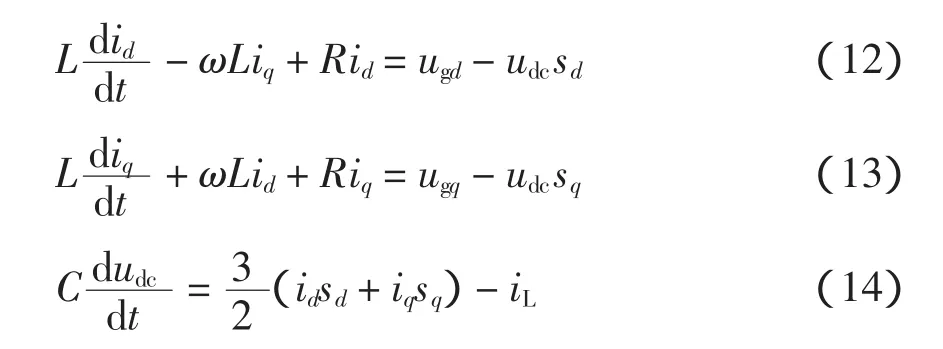
式中：ugd、ugq分别为电网电压dq轴分量，id、iq分别为AFE交流电流dq轴分量；ω为电网角频率，ω=dθ/d t；sd、sq分别为开关函数旋转变换后得到的占空比函数，稳态时sa、sb、sc的占空比按正弦规律变化，此时sd、sq为[－1，1]范围内的恒指常数。

由式（12）～式（14）得到dq坐标系下AFE系统的结构，如图2所示。

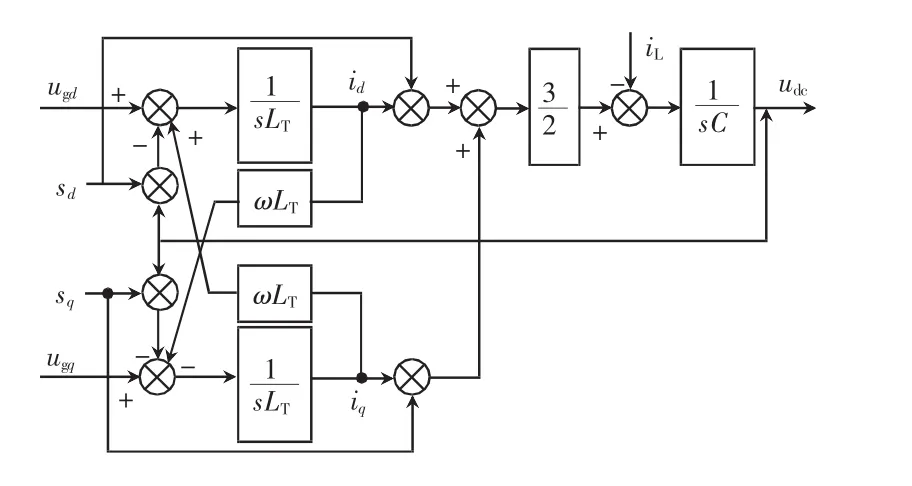
图2 dq坐标系下的AFE结构Fig.2 Structure of AFE in dq reference

2 AFE控制系统设计及参数整定

图2表明，调节sd、sq即可控制udc，电流id、iq相当于中间变量，为了实现较好的控制效果，需要对电压、电流分别设计控制器。

2.1 电流调节器设计

电流调节器采用常见的PI控制器。考虑到式（12）和式（13）中id、iq相互耦合，引入前馈解耦可以抑制其对控制的影响。解耦之后的电流调节方程为

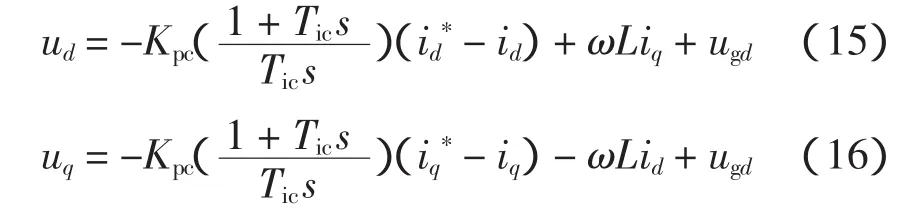
式中：Kpc、Tic分别为电流PI调节器的比例系数和积分时间常数。

根据式（15）、式（16），得到电流控制环如图3所示。

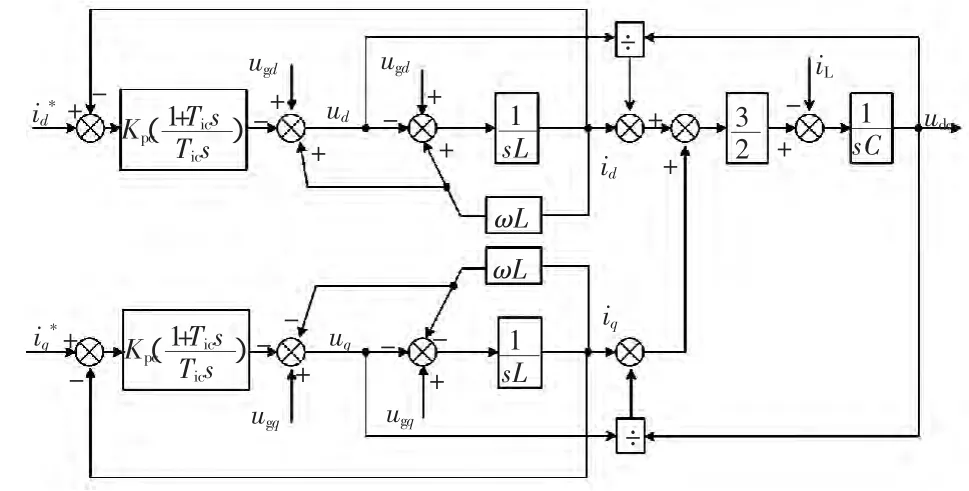
图3 电流控制环Fig.3 Current control loop

由图3可以看出，采用前馈解耦控制可将电流内环等效为一阶惯性环节，由于id、iq具有对称性，这里仅以id为例讨论电流调节器的参数整定方法。考虑PWM调制的效果，可以认为电流控制环包括4个环节，如图4所示。

图4 等效电流控制环Fig.4 Equivalent current control loop

图中，Tdu为对采样信号做滤波处理导致的延时；PWM环节代表AFE功率电路的放大及滞后效果，KPWM为放大增益，TPWM为AFE的失控时间，TPWM≈Ts/2；τ=L/R为电流环控制对象的时间常数；udis为考虑到电网电压变化及死时影响的等效扰动。

将图4中2个小时间常数的惯性环节合并，忽略小时间常数的高次项，得到等效惯性环节的增益为KPWM，时间常数近似等于1.5Ts。如果选择调节器的积分时间常数Tic=L/R，则电流环控制对象的一阶惯性环节可通过零极点对消，得到一个典型二阶系统，其传递函数为

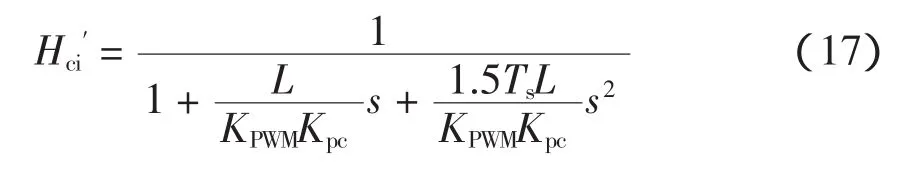
根据PI调节器的工程整定方法，令阻尼比为

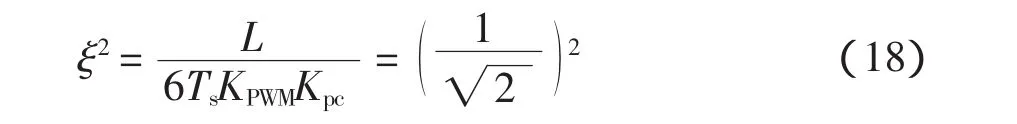
可得

由于式（17）中s2的系数远小于s的系数，因此忽略二次项，得到电流环的等效传函为

此时电流调节环的带宽近似为

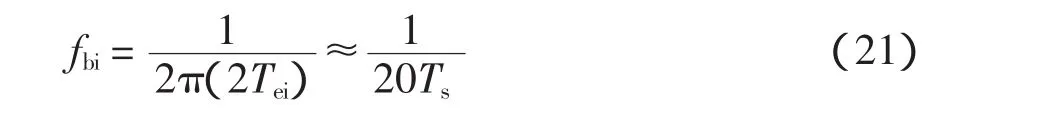
2.2 直流电压调节器设计

首先可通过功率关系确定出直流电压和id、iq的关系。在电网电压定向的dq坐标系下，AFE输入的瞬时有功和无功为

通常AFE运行在单位功率因数状态，iq=0，于是直流电压只和d轴电流有关。考虑到电流环已等效为一阶惯性环节，引入PI控制器作为调节器，简化电压控制环如图5所示。

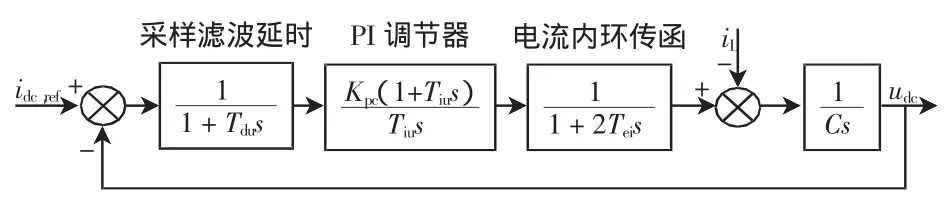
图5 电压控制环Fig.5 DC voltage control loop

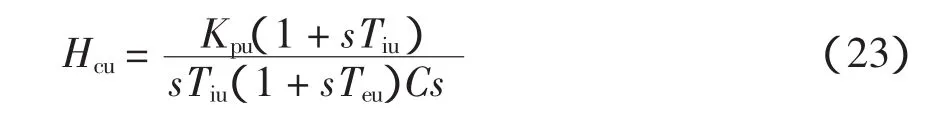
式中，Teu为等效电压环时间常数，Teu=Ts+2Tei。

采用“对称优化法”对式（23）中的PI控制器参数进行整定，Hcu的穿越频率、相位裕度与系统参数满足

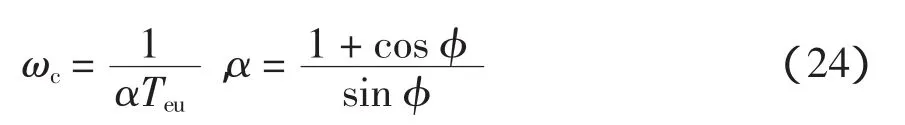
和电流环类似，电压环也可将小惯性环节合并并略除小时间常数的高阶项，得到等效一阶环节，即

式中：ωc为系统截止频率；φ为相角裕度；α为方便计算引入的比例系数，其计算式为因此，根据系统期望的截止频率和相位裕度，即可算出对应的Kpu和Tiu。

综合上述电压、电流控制环的结构，不难得出整个AFE系统的双闭环控制结构，如图6所示。

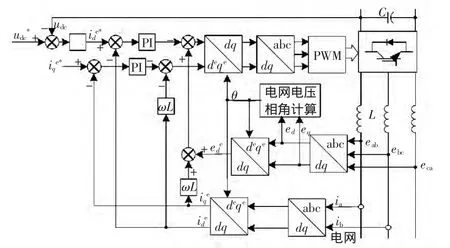
图6 AFE控制系统结构Fig.6 Structure of AFE control system

3 仿真验证

采用Matlab/Simulink软件对前述控制器设计及参数整定结果做了仿真验证，仿真系统结构如图1所示，其参数为：uga=311cos（100πt），V，网侧三相电压对称平衡；网侧等效电感、电阻分别为L=8mH，R=0.4Ω；直流侧电容C=2 200 μF；系统额定负载7.5 kW，采样时间200μs，采样滤波时间常数Tdu=1ms。由上述参数可算出电压环等效时间常数Teu=1.6ms；电流环和电压环调节器的参数为：Kpc=0.693，Tic=4ms，Kpu=5.294，Tiu=40ms。

图7给出了AFE系统突加负载时的启动过程。图中，AFE在0.5 s之前脉冲封锁，处于整流状态。从图7（b）可以看出，脉冲解封之前uab等于电网线电压；在0.5 s时刻，系统开始双闭环调节，脉冲解封，于是图7（a）中直流电压迅速上升至给定电压560 V，由于在参数设计中选择了较大的超调和截止频率，而且系统空载，因此udc的响应十分迅速，超调大约3.6%；在0.7 s时刻，直流侧突加7.5 kW电阻负载，直流电容对负载放电，导致直流电压突然降低，在双闭环调节作用下，电压迅速恢复至给定值，如图7（a）所示；由图7（c）可以看到，突加负载时网侧电流迅速增大，对应的有功输入迅速增大，支持直流电压的降低，说明电流环响应迅速且超调非常小；仿真中设置功率因数角为0，因此图7（c）中uga、ia同相。

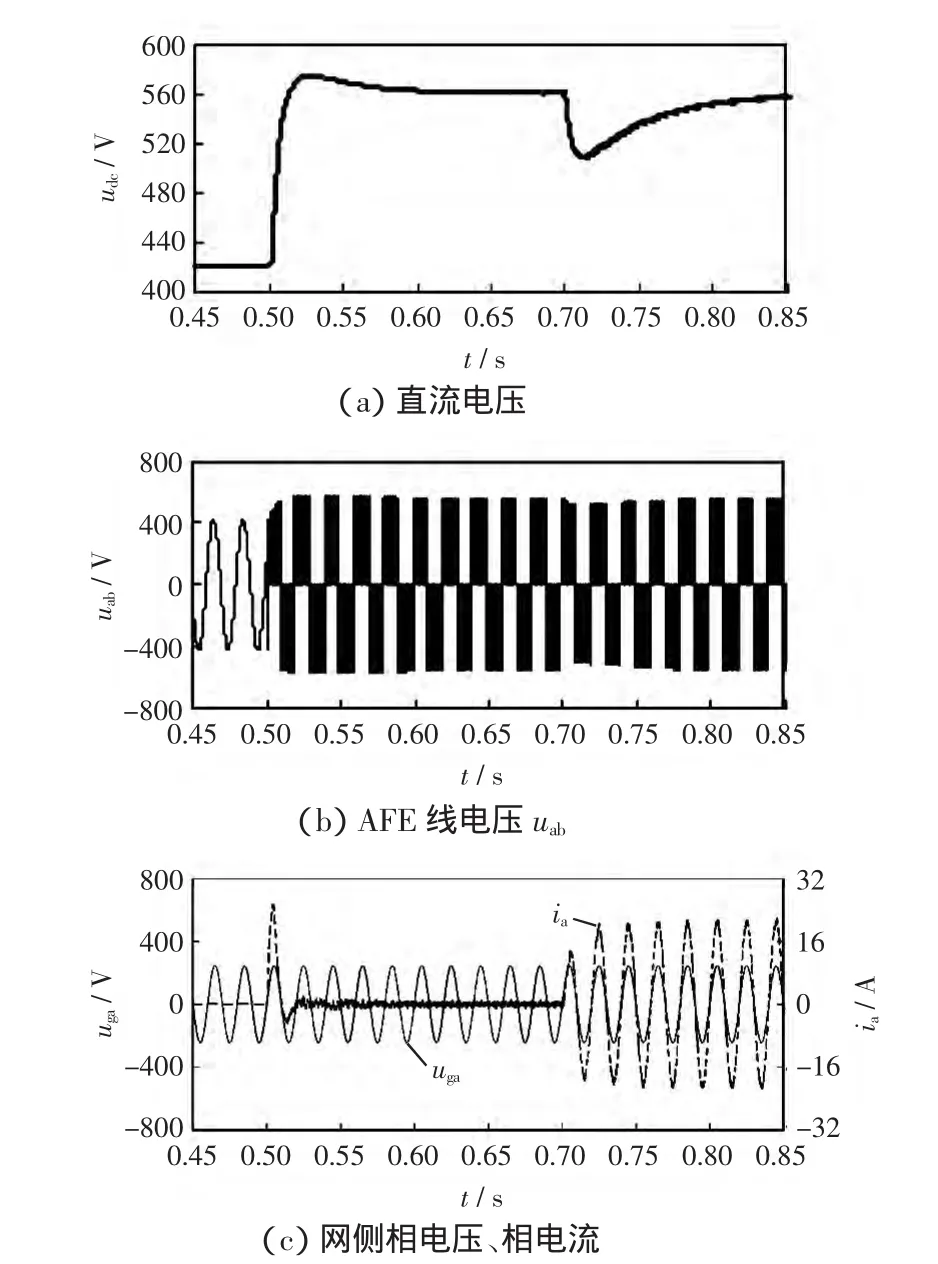
图7 AFE突加负载暂态过程Fig.7 Transient process of load disturbance for AFE

AFE向电网馈电时的电压、电流波形如图8所示。

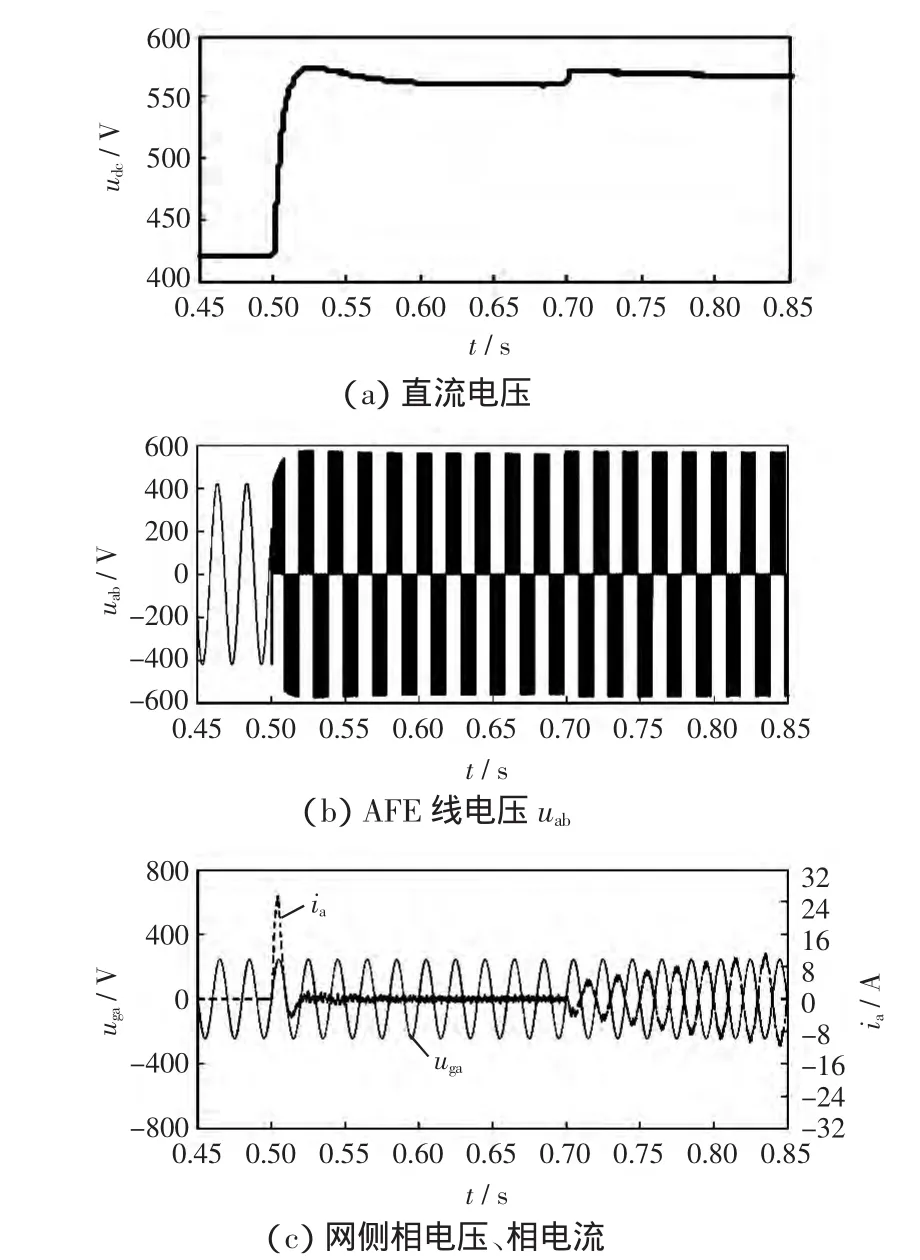
图8 AFE回馈运行Fig.8 Feedback operation of AFE

图中，AFE仍然是在0.5 s之前脉冲封锁，处于整流状态，0.5 s时刻解封后的电压、电流变化情况和图7相同。在0.7 s时刻，直流侧加入直流电源负载，且电压略高于AFE直流给定电压560 V，于是AFE开始向电网回馈电能。从图8（a）中可以看出，在负载电源加入瞬时，直流电压突然增加，之后在调节器的控制下逐渐趋于给定值。同时，网侧电流逐渐增加，AFE向电网馈入的能量逐渐增加，如图8（c）所示。由于无功电流给定为0，因此功率因数为-1，uga、ia反相。

综合图7、图8的结果，AFE的电压、电流调节迅速、准确，说明参数整定是有效可行。

4 结语

AFE作为一种灵活可控的整流器，具有网侧电流正弦、功率因数可调、可四象限运行等众多优点，已经在工业领域获得广泛应用。本文介绍了AFE系统在旋转坐标系下的数学模型，以此为基础设计了电压、电流双闭环控制器，采用“对称优化法”等频域分析方法整定了控制器参数。对实际物理系统的仿真结果验证了整定得到的PI参数能够满足稳定性及超调等指标要求。因此，所述建模及参数整定方法有效、可行，对实际系统设计具有很好的指导意义。

[1]AkagiH，Fujita，H.A new power line conditioner for harmonic compensation in power systems[J].IEEE Trans on Power Delivery，1995，10（3）：1570-1575.

[2]蔡逢煌，郑必伟，王武（CaiFenghuang，Zheng Biwei，WangWu）．单周期数字控制光伏并网逆变器的仿真与实验（Simulation and experimental of grid connected inverter based on one-cycle digital control）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（3）：97-100．

[3]王成山，李琰，彭克（Wang Chengshan，LiYan，Peng Ke）．分布式电源并网逆变器典型控制方法综述（Overview of typical control methods for grid-connected inverters of distributed generation）[J]．电力系统及其自动化学报（Proceedings of the CSU-EPSA），2012，24（2）：12-20．

[4]Habetler TG.A space vector-based rectifier regulator for AC/DC/AC converters[J].IEEE Trans on Power Electronics，1993，8（1）：30–36.

[5]Busse A，Holtz J.Multiloop control of a unity power factor fast switching AC to DC converter[C]//IEEE Power Electronics Specialist Conference.Cambridge，USA：1982.

[6]Akagi H，Kanazawa Y，Nabae A.Instantaneous reactive power compensators comprising switching devices without energy storage components[J].IEEE Trans on Industry Applications，1984，20（3）：625-630.

[7]Dewan S B，Wu R.A microprocessor-based dual PWM converter fed four quadrant AC drive system[C]//IEEE Industry Applications Society Annual Meeting.Atlanta，USA：1987.

[8]Wu R，Dewan SB，SlemonGR.APWMAC to DC converter with fixed switching frequency[C]//IEEE Industry Applications Society Annual Meeting.Pittsburgh，USA：1988.

[9]Wu R，Dewan SB，Slemon GR.Analysisofan AC-to-DC voltage source converter using PWM with phase and amplitude control[J].IEEE Trans on Industry Applications，1991，27（2）：355-364.

[10]张兴（Zhang Xing）．PWM整流器及其控制策略的研究（Study on the PWM Rectifier and Its Control Strategies）[D]．合肥：合肥工业大学电气与自动化工程学院（Hefei：School of Electrical Engineering and Automation，Hefei University of Technology），2003.

[11]Awad H，Svensson J，Bollen M J.Tuning software phase locked loop for series-connected converters[J].IEEE Trans on Power Delivery，2005，20（1）：300-308.