基于零空间的现代内点最优潮流新算法

全然，简金宝，韦化

（1.河南工业大学理学院，郑州 450001；2.玉林师范学院数学与信息科学学院，玉林 537000；3.广西大学电气工程学院，南宁 530004）

电力系统最优潮流是研究在满足系统运行和安全约束的前提下如何达到系统的最优运行状态的问题。随着电力系统规模的不断扩大和电力市场改革的不断深入，最优潮流OPF（optimal power flow）得到了广泛的关注和研究。Carpentier于1962年首先提出了严格数学基础上的最优潮流模型[1]，其实质是一个带一般约束的高维非线性最优化问题。求解最优化问题的许多方法都曾被用于求解OPF问题，如线性规划法、二次规划法、非线性规划法、牛顿法以及现代内点法等。

由于能有效求解大规模优化问题，现代内点法被广泛地应用于求解电力系统的各种优化问题，成为求解电力系统优化问题的主流算法，而且不断地被深入研究[2～10]，尤其是原始－对偶内点法[2～7]得到了广泛的应用和改进，取得了很好的效果。但仍存在一些问题需要研究，如算法的收敛性和计算速度等。文献[2]结合电力系统的特点，通过重新排列原始对偶变量的顺序使得修正方程组的系数矩阵出现与节点导纳矩阵有相似结构的4×4子块矩阵，显著地减少了注入元的个数，增加了稀疏性，取得了很好的计算效果；内点算法在文献[3～5]得到了进一步应用，取得了满意的计算效果，成为一种成熟的内点算法。这种算法为局部内点法。其显著特点是收敛速度快，计算时间短。但初始点选取不好可能会导致算法不收敛或收敛到不可行点，这将在第4节的数值实验分析中进行详细讨论；文献[11，12]也分别给出了简单的数值例子，从数学上说明上述“坏”情况确实会出现；文献[13]提出一种收敛性好的零空间内点算法NSIPM（null space interior point method）。该算法利用一个无约束二次规划的近似解作为预测步，再求解一个等式约束的二次规划得到一个零空间步作为迭代方向。算法具有良好的收敛结果。算法产生的点列要么收敛到松弛问题扰动的Karush－Kuhn－Tucher（KKT）点或原问题的FJ（Fritz－John）点，要么收敛于违背约束条件最小化问题的不可行稳定点。

本文把文献[13]中的NSIPM应用于求解OPF，通过改进终止准则和修正原始对偶变量能有效控制迭代点的可行性及松弛变量的互补性，保证迭代点趋于最优解，提高了算法的收敛性。对5个IEEE标准系统进行仿真分析，结果表明算法的收敛性好，收敛速度快。对于IEEE 14、118和300节点系统，压缩电压约束的范围，算法也能较好地收敛。对于IEEE 300节点系统，在一定范围内取不同初始点，算法均能较快收敛，对初值不敏感。这些结果都表明算法具有良好的收敛性和鲁棒性。

1 NSIPM简介

电力系统OPF问题的数学模型具体可描述为

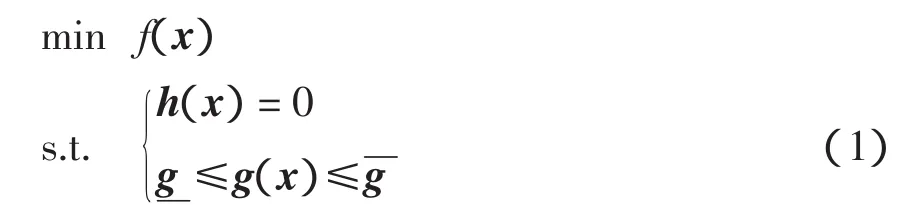
引入松弛变量l和u，则式（1）转化为松弛问题

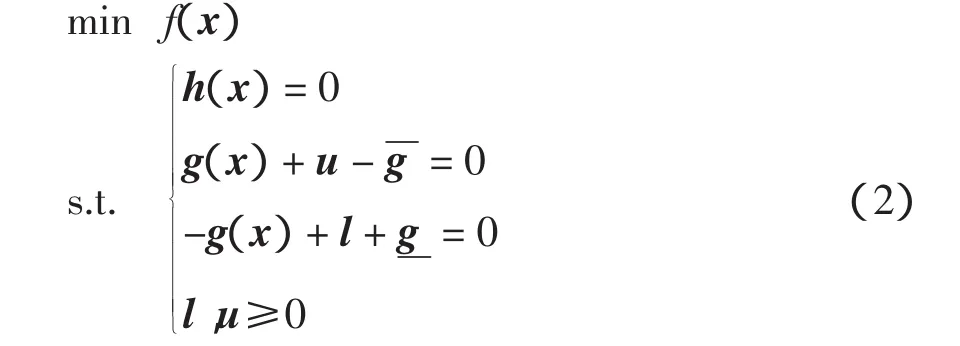
其扰动的KKT条件为

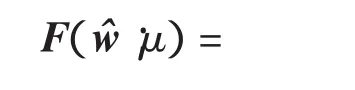
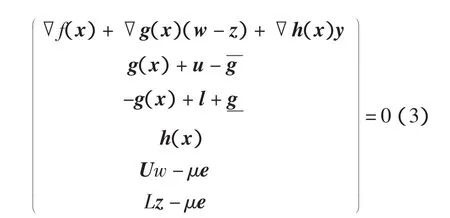
若初始点不可行，线性化等式可能会导致算法不收敛或收敛于不可行点。为克服这一不足，文献[13]提出了基于零空间技术的原始对偶内点算法，其实质是对线性化等式右端项的扰动，具体过程如下。

首先，记

式中：g=g（x）；h=h（x）；▽g=▽g（x）；▽h=▽h（x）；I为单位矩阵；B=▽2（ fx）+▽2g（x）（w-z）+▽2h（x）y；▽f=▽（fx）；W=diag（w）；Z=diag（z）。

文中‖·‖均为欧几里德范数，由带等式约束的二次规划的解产生零空间步，即

KKT条件为

根据文献[13]的引理2.3知，当Q在R的零空间上正定时，式（8）与式（9）同解，所以只需式（9）即可得到各变量的增量。令d=（Δx，Δu，Δl），p=（w+Δw，z+Δz，y+Δy），将具体的R，Q，q，d，p分别代入式（9），可得

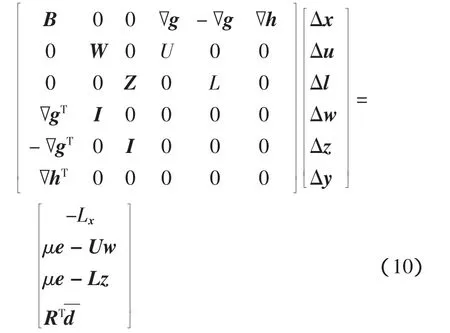
式中，Lx=▽f+▽g（w-z）+▽hy。形式上式（10）与文献[2]中的修正方程组相似，不同的是式（10）的右端项出现，若换为-r，则与文献[2]的修正方程组本质上一致。这里的可看作-r的扰动项。正是这一扰动，通过对的控制，使得NSIPM具有很好的收敛性和鲁棒性。文献[13]假设满足条件为

式中：κ1、κ2为正常数；矩阵在此条件下，再利用一定的假设条件，文献[13]证明了NSIPM具有全局收敛性和局部超线性收敛性。尤其具有良好的全局收敛性，即文献[13]中的定理4.10：算法产生的点列要么收敛到问题式（2）的扰动的KKT点（即满足式（3））或原问题的FJ点，要么收敛于违背约束条件最小化问题的不可行稳定点。

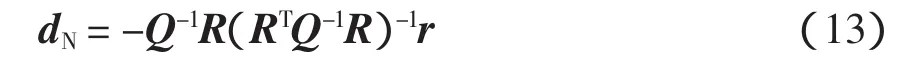
若

则取

式中：ν∈（0，1）；ψ为式（7）中的目标函数。

否则计算

再在dC和dN张成的子空间中求预测步，使得

利用效益函数进行线搜索

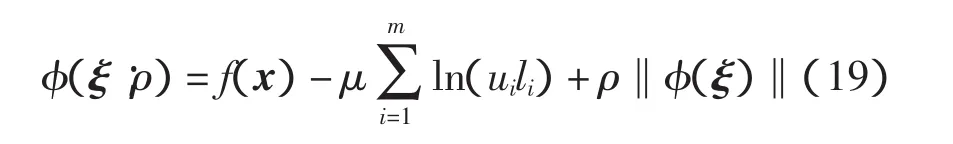
式中：ξ=（x，u，l）；ρ为罚参数；m为式（1）中不等式约束的个数，即g（x）的维数，且φ（ξ）=（g+u-，-g+l+，h）。效益函数φ（ξ；ρ）为l2罚函数，不可微，由文献[14]的命题3.1可知，其方向导数为

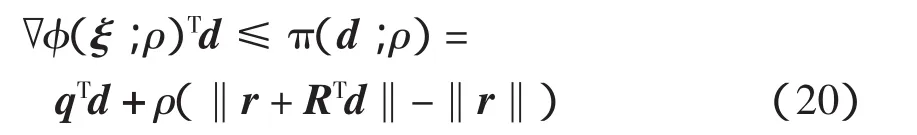
在当前迭代点ξk（k表示第k次迭代，下同）处，为使效益函数值有所下降，迭代步长αk应满足

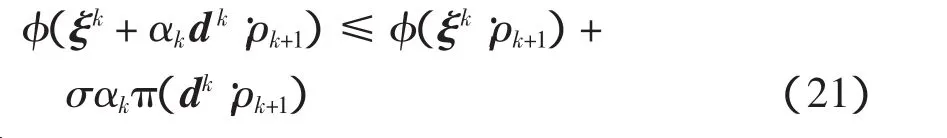
式中，σ∈（0，1/2）。

下面给出罚参数ρk+1的取值方法[13]。先计算

式中，τ∈（0，1）。从而取罚参数ρk+1为

求取原始对偶变量的初始最大步长为

2 OPF模型

本文采用的OPF模型中，目标函数和约束函数依次为

（1）目标函数采用发电燃料费用，即

（2）等式约束为潮流方程，即

（3）不等式约束为运行约束，即

式（25）～式（27）中：v=（PG，QR，e，f）；ei+j fi为节点i的电压复相量分别为节点电压幅值上下限的平方值；a2i、a1i、a0i分别为火电厂i的燃料系数；PG，i、QR，i分别为节点i上的可调有功出力和无功出力分别为其上下限；PDi、QDi分别为节点i上的有功负荷和无功负荷；Gij+j Bij为节点i与j之间的互导纳；SG为发电机节点集合；SR为无功电源集合；SN为节点集合；SL为约束线路集合Bij为传输线i-j上的有功潮流，Pij，Pij分别为其上下限。

3 算法步骤

求解OPF问题的NSIPM计算步骤[13]如下。

步骤1初始化：设k=l=0；τ，β∈（0，1）；σ，μ，η，γ1，γ2＞0；ρ0=10；ε=10－5。

步骤4解式（10），得到各变量增量。

步骤5根据式（23）调整罚参数ρk+1。

步骤6进行线搜索确定步长αk：由式（24）确定原始对偶变量的初始最大步长sp和sd。取αk=spβθ，θ为使得式（21）满足的最小非负整数。更新变量值

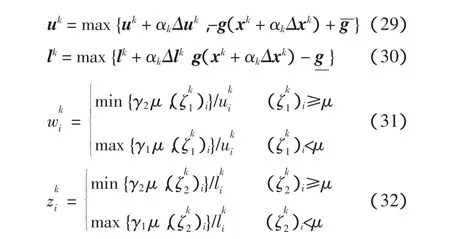
其中

令yk=yk+Δyk；k=k+1，转入步骤3。

步骤7减小参数μ的值，l=l+1，转入步骤2。

由于关于对偶变量wk，zk的修正不易执行[13]，步骤6给出对偶变量新的修正形式。此修正方法仍能使得Ukwk、Lkzk的每一个分量均属于区间[γ1μ，γ2μ]，且（Ukwk，Lkzk）→（μe，μe）。当μ→0时，能保证松弛变量的互补性，即（Uw，Lz）=（0，0）。

迭代过程中，‖F（w^k；μ）‖趋于0，但‖F（w^k；μ）‖有时产生波动，影响算法的收敛速度。这是因为NSIPM采用的效益函数不能保证‖F（w^k；μ）‖在每一次迭代时下降。数值仿真表明波动主要是受‖F（w^k；μ）‖中的▽f（xk）+▽g（xk）（wk-zk）+▽h（xk）yk的影响，去掉此项，记F（w^k；μ）中剩下部分为Z（ϖk；μ）=（rk，Ukwk－μe，Lkzk－μe），则在迭代过程中‖Z（ϖk；μ）‖平稳下降且趋于0。由式（3）可知，Z（ϖk；μ）中的rk为OPF问题的潮流约束和运行约束，Z（ϖk；μ）中的（Ukwk－μe，Lkzk－μe）为松弛变量的互补性条件。当‖Z（ϖk；μ）‖→0时，可保证OPF问题迭代点的可行性和互补性。因此，为减少迭代过程中的波动，加快收敛速度，在算法执行时，将步骤2和步骤3的收敛准则中的F（w^k；μ）换为Z（ϖk；μ），具有实际意义。

4 数值实验

利用本算法，使用Matlab 7.1编写程序，对IEEE14、30、57、118及300节点系统进行数值实验。计算环境为：AMD Athlon（tm）64×2Dual Cone Processor3800+，896MBRAM，Windows XP。测试系统的基本参数见表1。算法执行时，参数分别设置为：μ=0.9；η=500；γ1=0.000 1；γ2=600；β=0.5；σ=0.01；τ=0.5。算法步骤7中取μ=0.1μ。

表1 测试系统参数Tab.1 Parameters of test system

记本文算法为“算法1”，文献[2]的内点算法为“算法0”，2种算法在平启动和电压约束上下界分别为=1.1和=0.9时的计算结果见表2。由表2可以看出，2种算法的迭代次数相差不大。

表2 算法1与算法0的迭代结果Tab.2 Iteration results of algorithm s1 and 0

为加快收敛速度，去掉算法1中的线搜索步骤，借鉴文献[2]中的步长取法，步骤6中取αk=sp；yk=yk+sdΔyk，这样的算法记为“算法2”。虽然类似于文献[2]中的原始对偶变量的步长取值，但两者不一样。本文在步骤6中对原始变量u、l和对偶变量w、z进行了二次修正。

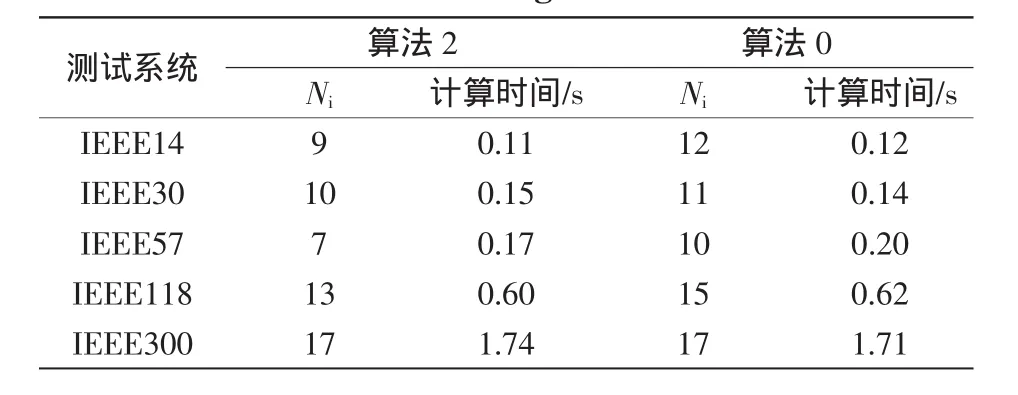
表3 算法2与算法0的计算结果Tab.3 Results of algorithm s2 and 0

图1 算法2对IEEE 118和300节点系统的迭代收敛过程Fig.1 Convergence procedure of algorithm 2 for IEEE 118 and 300-bus system s

其平稳地下降到误差范围内，很好地保证了迭代点的可行性、松弛变量的互补性和迭代点的最优性。说明改进的收敛准则和对偶变量的修正方法有效。分别以IEEE 14、118和300节点系统为例，通过与算法0比较说明算法1和算法2具有良好的收敛性。首先以IEEE 14节点系统为例，增大电压约束下界，减小上界，使电压约束更严格。经过实验，当时，算法0在平启动时不收敛，而算法1经过25次迭代后收敛；然后以IEEE 118节点系统为例，与算法0比较说明算法2具有良好的收敛性。此时算法2中的部分参数值调整为：η=5；γ1=0.05；在步骤7中取μ=0.08μ。增大电压约束下界Vi，减小上界经实验，当时，算法0在平启动时不收敛，而在此条件下算法2收敛。对上界V进行小扰动，取Vi=，在平启动时，算法0仍不收敛，算法2收敛，说明算法2具有良好的收敛性。这2种情况的迭代结果如表4所示。表4中电压虚部初值f=0，实部初值取5种情况，其中a1=算法2与算法0分别在平启动时对IEEE 118节点系统的收敛迭代过程如图2所示。为清晰起见，图2中从第60次迭代开始。算法0的收敛判断值，即文献[2]中的互补间隙为

最后以IEEE 300节点系统为例，将算法2与算法0进行比较。压缩电压上下界，下界为原来的1.01倍，上界为原来的0.935 614倍。算法0在平启动时不收敛，而算法2收敛。在此电压上下界条件下，电压虚部初值为0，实部取不同初值时2种算法的迭代结果见表5。由表5可见，算法2具有良好的收敛性。

表4 算法2与算法0对IEEE 118节点系统的迭代结果Tab.4 Iteration results between algorithms2 and 0 for IEEE 118-bus system

图2 算法2与算法0对IEEE118节点系统收敛迭代过程Fig.2 Convergence procedure between algorithms2 and 0 for IEEE 118-bus system

表5 算法2与算法0对IEEE 300节点系统的迭代结果Tab.5 Iteration results between algorithms2 and 0 for IEEE 300-bus system

5 结语

本文将NSIPM应用于求解OPF，通过预测步和零空间步来产生搜索方向，改进的收敛准则和对偶变量修正方法能有效控制迭代点的最优性和松弛变量的互补性。5种IEEE算例的数值结果表明，无论是在约束条件苛刻还是在一定范围内取不同初始迭代点，本文算法均能收敛到最优解，具有良好的收敛性和鲁棒性。

[1]Carpentier J.Contribution to the economic dispatch problem[J].Bulletin de ls Societe Francaise des Electriciens，1962，（8）：431-437.

[2]Wei Hua，Sasaki H，Kubokawa J，et al.An interior point nonlinear programming for optimal power flow problems with a novel data structure[J].IEEE Trans on Power Systems，1998，13（3）：870-877.

[3]韦化，李滨，杭乃善，等（WeiHua，LiBin，Hang Naishan，et al）.大规模水-火电力系统最优潮流的现代内点理论分析（An analysis of interior point theory for large-scale hydrothermal optimal power flow problems）[J].中国电机工程学报（Proceedings of the CSEE），2003，23（4）：5-8.

[4]韦化，丁晓莺（WeiHua，Ding Xiaoying）.基于现代内点理论的电压稳定临界点算法（An algorithm for determining voltage stability critical point based on interior point theory）[J].中国电机工程学报（Proceedings of the CSEE），2002，22（3）：27-31.

[5]丁晓莺，王锡凡，张显，等（Ding Xiaoying，Wang Xifan，Zhang Xian，et al）.基于内点割平面法的混合整数最优潮流算法（Mixed integer optimal power flow based on interior point cutting plane method）[J].中国电机工程学报（Proceedings of the CSEE），2004，24（2）：1-7.

[6]黄镇，杨京燕，覃智君，等（Huang Zhen，Yang Jingyan，Qin Zhijun，et al）.采用内点法的多目标低电压风险优化（Interior point method based multi-objective optimization of low voltage risk）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2011，23（2）：92-97.

[7]李晓莉（LiXiaoli）.考虑支路电压稳定指标的无功定价新模型（Reactive power pricing model considering line voltage stability index）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2010，22（5）：156-160.

[8]陈妍，黄民翔（Chen Yan，HuangMinxiang）.基于信赖域内点法的静态ATC计算（Static ATC calculation based on a trust region interior-point method）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（5）：71-74.

[9]余娟，颜伟，李文沅（Yu Juan，YanWei，LiWenyuan）.考虑发电机安全运行极限的非固定分段无功优化模型及其算法（An unfixed piecewise model of reactive optimization and its algorithms considering generator capability limits）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（7）：23-28.

[10]YuchiW，Debs A S，Marsten R E.A direct nonlinear predictor-corrector primal-dual interior point algorithm for optimal power flows[J].IEEE Trans on Power Systems，1994，9（2）：876-883.

[11]Wachter A，Biegler L T.Failure of global convergence for a class of interior point methods for nonlinear programming[J].Mathematical Programming，2000，88（3）：565-574.

[12]Byrd R H，Marazzi M，Nocedal J.On the convergence of Newton iterations to non-stationary points[J].Mathematical Programming，2004，99（1）：127-148.

[13]Liu Xinwei，Yuan Yaxiang.A null-space primal-dual interior-point algorithm for nonlinear optimization with nice convergence properties[J].Mathematical Programming，2010，125（1）：163-193.

[14]Liu Xinwei，Sun Jie.A robust primal-dual interior-point algorithm for nonlinear programs[J].SIAM Journal on Optimization，2004，14（4）：1163-1186.