WPSEG法在GIS故障识别中的应用

王春亮，马宏忠，徐天乐

（河海大学能源与电气学院，南京 210098）

气体绝缘全封闭组合电器是将断路器、隔离开关、快速接地开关、电流互感器、电压互感器、避雷器、母线、套管和/或电缆终端等电气元件封闭组合在接地的金属外壳中，内部充以0.3～0.4MPa的SF6气体作为绝缘介质的开关电器[1]。它具有体积小、占地面积小、运行可靠性高、不受外界环境影响、配置灵活、维护工作量小、检修周期长、无电磁干扰等优点[2]，在城市电网建设和改造中广泛应用。但GIS一旦出现故障，会造成严重后果，并且其检修周期较长。因此，有必要加强对GIS在线监测与故障诊断的研究。

局部放电PD（partial discharge）检测是一种评估GIS早期绝缘缺陷的有效手段[3～4]，本文针对现有的GIS 4种典型局部放电缺陷分析。

小波熵是小波分析和信息熵原理相结合的产物[5～6]，其基本思想是把小波变换系数矩阵处理成一个概率分布序列，用该序列的熵值来反映这个系数矩阵的系数程度，及被分析信号概率分布的有序程度。基于不同的原理和处理方法，目前主要用来表征信号的方法有小波时间熵、小波能量熵、小波奇异熵、小波时频熵[7]。本文在小波奇异熵理论的基础上提出小波包奇异能量值法，并与小波包奇异熵法进行对比分析，结果表明WPSEG法在GIS局放缺陷识别中的有效性及优越性。

1 WPSEG法原理

小波包变换具有良好的时频局部化特性，能较好地反映被分析信号的时频特性，文献[8～10]对其有详细分析，本文不再赘述。

奇异值分解是一种非线性滤波，广泛应用于信号检测中。文献[11]阐述了矩阵的奇异值对于矩阵元素的扰动变化是不敏感的，具有相对稳定性。此外奇异值还具有位移不变性和旋转不变性[12～14]。上述特性都可说明，当矩阵存在一定干扰和分散时，矩阵的奇异值都具有较为稳定的矩阵代数特征参量。在SVD理论中，任何m×n阶的矩阵A的SVD都可表示[15]为

式中：U和V分别为m×m和n×n阶矩阵；Λ=diag（λ1，λ2，…，λn）为对角矩阵，其对角元素为A的奇异特征值，并且它们都是降序排列的。由于Λ是一对角阵，因此SVD可将一个秩为k的m×n阶矩阵A表示为k个秩为1的m×n阶子矩阵的和。其中，每个子矩阵由2个特征矢量（分量分别来自U和V）和权值相乘得到，即

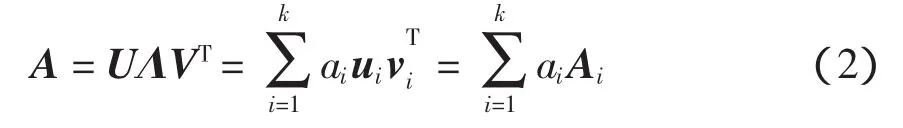
式中：k为A的秩；ui、vi（i=1，2，3，…）分别为U和V的第i列奇异值矢量；Ai为包含ui和vi的子矩阵。

由于故障类型不同，仅依靠信号的时频直观分布还不足以明确识别各状况下的故障类型，而且变换后的数据量很大，因此有必要通过SVD理论对小波包变换系数矩阵进行预变换处理。

WPSEG是基于小波包变换、SVD及能量值法的综合分析方法，将信号经小波包分解重构的系数矩阵分解为一系列能反映原系数矩阵基本特征的奇异特征值，这些特征值构成序列[λ1，λ2，…，λn]，定义该特征值序列在L2（R）上2的范数[13]定义为

奇异特征值序列的2的范数的平方等价于该序列信号在时域上的能量。

2 小波包奇异熵

小波包奇异熵是小波包变换、奇异值分解和信息熵的有机结合，将小波包分解重构系数矩阵经奇异值分解得到一系列奇异特征值λ1，λ2，…，λn，为了定量描述信号的频率成分及分布特征，定义WPSEP为

式中，Δpi为第j阶增量小波包奇异熵。

小波包空间的奇异熵，在综合冗余信息的基础上，直接反映了被分析信号时频空间中特征模式能量的分布不确定性。被分析信号越简单，能量越集中于少数几个模式，WPSEP越小；相反，信号越复杂，能量就越分散，WPSEP越大。因此，上述定义的奇异谱熵给出了一个在整体上衡量信号复杂性或不确定性程度的指标。

3 基于WPSEG法的GIS故障识别

GIS最常见的电气故障特征是绝缘击穿或闪络前发生局部放电，本文采用现有的GIS 4类超高频局部放电缺陷进行缺陷识别分析。

（1）高压导体金属突出物缺陷（N类缺陷）：高压导体表面金属突出物通常是由于不良加工、机械破坏或组装时的擦刮而出现的[16]。如图1所示。

图1 高压导体金属突出物缺陷仿真信号Fig.1 Simulated signal of protrusion fixed to the HV conductor

（2）自由金属微粒缺陷（P类缺陷）：该类缺陷是GIS中最常见同时也是危害最大的缺陷。微粒运动的程度取决于微粒的形状大小、材料性质和外施电压高低，以及微粒处于GIS腔体内的位置等因素[16]。如图2所示。

图2 自由金属微粒缺陷仿真信号Fig.2 Simulated signal of free metal particles

（3）绝缘子表面固定金属微粒缺陷（M类缺陷）：自由金属微粒在GIS中运动时，如果长期地固定在绝缘子表面，就会形成绝缘子表面金属污染缺陷[16]。如图3所示。

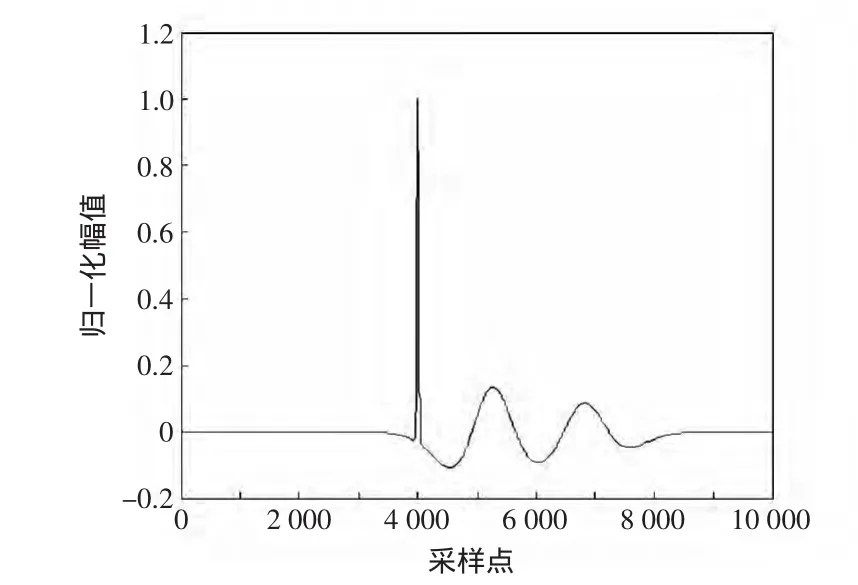
图3 绝缘子表面固定金属微粒缺陷仿真信号Fig.3 Simulated signal of surface contamination on the insulator

（4）气体缺陷（G类缺陷）：在GIS内部，当固体绝缘子和内导体间的交界处出现一定的间隙时，增加了交界处的电场强度，会产生损害固体绝缘子的局部放电，造成GIS绝缘破坏[16]。如图4所示。

图4 气隙缺陷局仿真信号Fig.4 Simulated signal of electrode gap defect

对上述4种缺陷情况首先采用2层小波包分解和3层小波包分解分别得到表1和表2所示的奇异特征值和WPSEG值。

表1 故障信号的奇异特征值和WPSEG值（2层）Fig.1 Singular eigenvalue and WPSEG of fault signal（2 levels）

表2 故障信号的奇异特征值和WPSEG值（3层）Fig.2 Singular eigenvalue and WPSEG of fault signal（3 levels）

从表1和表2中可以看出，不同故障类型分解得到的奇异特征值和WPSEG值是不同的，并且每类故障分解得到的奇异特征值均按降序排列，奇异特征值越小，其反映信号的信息量越少。对比表1和表2可以发现，同类故障小波包分解层数虽然不同，但求得的WPSEG值却是一定的，如N类故障的WPSEG值都是207.807 1，并且可以看出计算值大小规律为N＞G＞M＞P，对4层及4层以上的分解可以得到同样的结果。根据上述分析，本文利用WPSEG值的差异来识别GIS的故障类型是行之有效的。

考虑实际信号经奇异值变换后的非零奇异值的阶数可能很大，即λ1，λ2，…，λp中的p可能很大，并且随着p的增大，λp值减小，即λp反映的信息量减少，利用价值减小，因此为降低复杂度，常根据实际情况忽略较小的奇异特征值而取前α个（1≤α≤p）奇异特征值（λ1，λ2，…，λα）来代替（λ1，λ2，…，λp）来描述原系数矩阵的基本特征，但其必须满足约束条件：λα/λ1≥0.01%。

实际采集到得信号不可避免地会存在各种干扰的影响，本文对4类缺陷均加信噪比为1的白噪声，4类故障信号的染噪信号如图5（a）～（d）所示。

从表3中可以看出，对于染噪的故障信号，求得4类缺陷的WPSEG值，由于受到噪声影响，WPSEG值较加噪前的值明显增加，但是依然可以根据其WSEPG值的大小（N＞G＞M＞P）判断出4类故障。

图5 四种缺陷的染噪信号Fig.5 Noised signals of four kinds of defects

表3 染噪故障信号的奇异特征值和小波包能量值（3层）Fig.3 Singular eigenvalue and WPSEG of noised fault signal（3 levels）

定义染噪前、后信号的小波包奇异能量值分别为WPSEG1、WPSEG2，定义它们比值为

3层小波包分解时4类故障的K值如表4所示。

表4 K值表Fig.4 Table of K-value

从表4中可以看出，GIS4类故障的K值几乎相等，分析结果说明，在同种白噪声环境下，4类故障的WPSEG值是成比例增长的，不会影响到故障类别的判定，对于其他类型的噪声影响需要进一步研究。

由表2和表3所得出的故障信号染噪前、后的奇异特征值计算不同故障类型的WPSEP值，如表5所示。

表5 故障信号染噪前、后的WPSEP值Fig.5 WPSEP of fault signals before and after being noised

从表5可以看出，无论是染噪前还是染噪后都很难通过WPSEP值的大小来判断故障类型，尤其是染噪后，求得的信息熵几乎完全一样。分析表明，WPSEG值法与WPESP值法相比前者更优。

4 结语

针对GIS局部放电的特点，本文结合小波包变换、奇异值分解及能量值法，提出WPSEG值法对GIS 4类缺陷信号进行识别，结果表明，该方法克服了小波包分解层数以及白噪声对分析结果的影响，能够有效识别4类UHF局放缺陷。

[1]王昌长，李福祺，高胜友.电力设备的在线监测与故障诊断[M].北京：清华大学出版社，2006.

[2]杨圆，李成榕（Yang Yuan，LiChengrong）.典型GIS局部放电超声波信号特征研究（Study on ultrasonic characteristics of typical partial discharge of GIS）[J].现代电力（Modern Electric Power），2009，26（5）：18-23.

[3]Kaneko S，Okabe S，Yoshimura M，et al.Detecting characteristics of various type antennas on partial discharge electromagnetic wave radiating through insulating spacer in gas insulated switchgear[J].IEEE Trans on Dielectrics and Electrical Insulation，2009，16（5）：1462-1472.

[4]DingW，Ochi K，Suehiro J，et al.Factors affecting PD detection in GIS using a carbon nanotubegas sensor[J].IEEE Trans on Dielectrics and Electrical Insulation，2007，14（3）：718-725.

[5]Rosso OA，Blanco S，Yordanova J，et al．Wavelet entropy：a new tool for analysis of short duration brain electrical signals[J]．Journal of Neuroscience Methods，2001，105（1）：65-75.

[6]Blanco S，Figliola A，Quiroga R Q，et al．Time-frequency analysis of electroencephalogram series.III.Wavelet packets and information cost function[J].Physical Review E，1998，57（1）：932-940．

[7]何正友，符玲，麦瑞坤，等（He Zhengyou，Fu Ling，Mai Ruikun，et al）.小波奇异熵及其在高压输电线路故障选相中的应用（Study on wavelet singular entropy and its application to faulty phase selection in HV transmission lines）[J].中国电机工程学报（Proceedings of the CSEE），2007，27（1）：31-36.

[8]葛哲学，沙威.小波分析理论与MATLAB2007实现[M].北京：电子工业出版社，2007.

[9]杨文志，马文生，任学平（YangWenzhi，MaWensheng，Ren Xueping）.小波包降噪方法在滑动轴承故障诊断中的应用研究（Application of wavelet packet denoising method in fault diagnosis of bearings）[J].噪声与振动控制（Noise and Vibration Control），2009，50（4）：50-53.

[10]潘文霞，李春林，史林军（Pan Wenxia，Li Chunlin，Shi Linjun）.基于最佳小波包基的电能质量暂态数据压缩（Power quality transient disturbance compression based on optimum wavelet packet）[J].电力系统及其自动化学报（Proceedings of the CSU-EPSA），2005，17（3）：50-54.

[11]杜林，戴斌，陆国俊，等（Du Lin，Dai Bin，Lu Guojun，et al）.基于S变换局部奇异值分解的过电压特征提取（Overvoltage features extraction based on S transform and local singular value decomposition）[J].电工技术学报（Transactions of China Electrotechnical Society），2010，25（12）：147-153.

[12]洪子全，杨静宇（Hong Ziquan，Yang Jingyu）.基于奇异值特征和统计模型的人像识别算法（Human facial image recognition algorithm based on singular value feature and statistical model）[J].计算机研究与发展（Journal of Computer Research and Development），1994，31（3）：60-65.

[13]闫荣华，彭进业，李岩，等（Yan Ronghua，Peng Jinye，Li Yan，et al）.基于小波域奇异值分解的人脸识别方法（Method of face recognition based on sigular value decomposition in the wavelet domain）[J].计算机工程（Computer Engineering），2007，33（4）：212-214，217.

[14]甘俊英，张有为（Gan Junying，Zhang Youwei）.一种基于奇异值特征的神经网络人脸识别新途径（A new approach for face recognition based on singular value features and neural networks）[J].电子学报（Acta Electronica Sinica），2004，32（1）：170-173.

[15]周璐，黄纯，张秋丽，等（Zhou Lu，Huang Chun，Zhang Qiuli，et al）.基于SVD-prony的消除暂态超越的新算法（A novel algorithm for eliminating transient overreach）[J].电力系统及其自动化学报（Proceedings of the CSUEPSA），2011，23（4）：122-127.

[16]周倩（Zhou Qian）.组合电器局部放电超高频信号数学模型构建和模式识别研究（Study on Mathematical Model and Pattern Recognition for Ultra-high Frequency Partial Discharge Signals in GIS）[D].重庆：重庆大学电气工程学院（Chongqing：College of Electrical Engineering of Chongqing University），2007.