Anti-plane Circular Nano-inclusion Problem with Electric Field Gradient and Strain Gradient Effects
2014-04-14ShashaYangandShengpingShen
Shasha Yang and Shengping Shen
1 Introduction
Developments of nanotechnology in recent decades motivate progress in research of nanocomposites.Nano-scale inclusion,as an essential part of nanocomposites,has been investigated through various theories which are proposed to account for size effect[Wang,Pan and Feng(2008)].To name a few,couple stress elasticity[Wang,Pan and Feng(2008);Lubarda(2003)],micropolar theory[Cheng and He(1995)],strain gradient elasticity[Zhang and Sharma(2005)],electric gradient theory[Yang,Zhou and Li(2006);Mindlin(1968)],surface theory[Sharma and Ganti(2004);Yang,Hu and Shen(2012)]and so on.Herein special attention is focused on gradient theories.
Recently,Gao and Park(2007)provided explicit variational formulation for a simplified strain gradient elasticity theory(SSGET)which contains only one material length scale parameter.Then size-dependent Eshelby tensors of spherical,plane strain,cylindrical,ellipsoidal and anti-plane inclusion based on SSGET were obtained in a series of articles[Gao and Ma(2009);Ma and Gao(2010);Gao and Ma(2010,2012)].Yang,Zhou and Li(2006)analyzed the effect of electric field gradient in anti-plane problem of a circular inclusion in polarized ceramics.These individual gradient theories promote researchers to combine strain gradient and electric field gradient theory into a unified framework.Hu and Shen(2009)proposed a variational principle considering both the electric field gradient and strain gradient,as well as surface effect and electrostatic force for nano-dielectrics.The theoretical framework can describe size effect,electromechanical coupling and surface effect simultaneously.Basing on polarization gradient and strain gradient,Shen and Hu(2010)developed a framework which took flexoelectric effect,surface effect and electrostatic force into account.Flexoelectric effect[Cross(2006);Zubko,Catalan and Tagantsev(2013)],defined as coupling of strain gradient and polarization(direct effect)and coupling of polarization gradient and strain(inverse effect),have been investigated extensively on inclusion[Maranganti,Sharma and Sharma(2006);Sharma,Maranganti and Sharma(2007)],beam[Yan and Jiang(2013);Liang and Shen(2013)],thin-film[Sharma,Landis and Sharma(2010)]and other topics[Liu,Hu and Shen(2012),(2014);Xu,Hu and Shen(2013)].It is emphasized thatpolarization gradientand electric field gradientcan alternatively be chosen to represent flexoelectric effect[Ma(2008)].Moreover,electric field gradient shows lower symmetry,and this character makes process and results of solving problems simpler and more explicit than polarization gradient consideration.Until now,Eshelby-type nano-inclusion problem including both strain gradient and electric field gradient effect has not been studied yet.In this study,we analyze antiplane nano-scale inclusion problem with electric field gradient and strain gradient effects.
The outline of this paper is as follows.In Sec.2 the general formulation is given for isotropic centrosymmetric dielectrics.Then anti-plane nano-inclusion problem is analyzed in Eshelby’s frame by means of Green’s function method in Sec.3.Sec.4 gives the analytical expression for anti-plane circular inclusion with corresponding numerical results in Sec.5.Finally,a few concluding remarks are provided in Sec.6.
2 General formulas
The governing equations and boundary conditions including strain/electric field gradient effect and surface effect[Hu and Shen(2009)]are derived through the variational principle.Refer to[Hu and Shen(2009)],the general expression for electric Gibbs free energy density function involving the gradients of strain and electric field can be written as:

Within the assumption of centrosymmetric dielectrics,the odd tensors will vanish according to Neumann principle.The expression ofUbcan be simplified as:
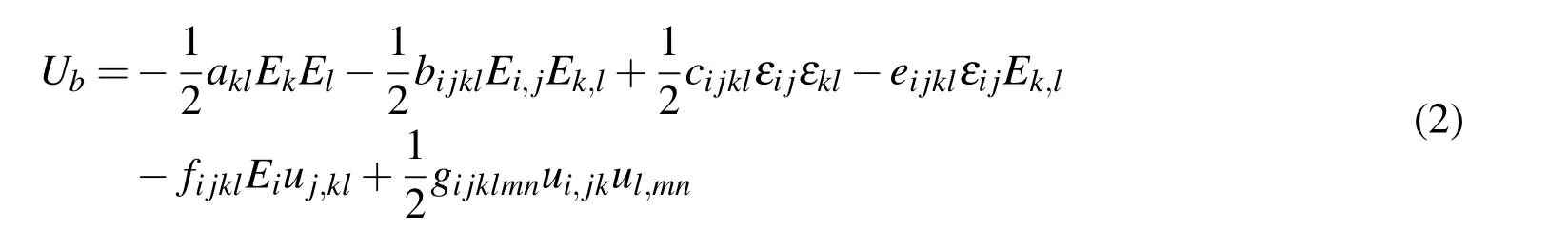
where a and c are the classical second-order dielectric permittivity tensor and fourorder elasticity constant tensors respectively.f is the flexoelectric tensor while e is the converse flexoelectric tensor according to definitions in Shu et al.(2011).b and g represent purely electric field and elastic nonlocal effect respectively.u and E are the displacement and the electric field tensor,while the subscript comma indicates differentiation with respect to the spatial variables.Additionallyεis the strain tensor defined as usual.
According to Hu and Shen(2009),the constraints relation are defined as:

whereφis the electrostatic potential.w and V are the strain gradient tensor and the electric field gradient tensor respectively.The symmetry of the tensors are showed as:εij=εji,wijm=wjim,Vij=Vji.
Under the infinitesimal deformation assumption,the constitutive equations can be expressed as:

The governing equations are written as:

Fiandρare external body force and body electric charge,respectively.By substituting Eqs.(7)-(10)into Eq.(11)and Eq.(12),the general governing equations based on u andφcan be derived as:
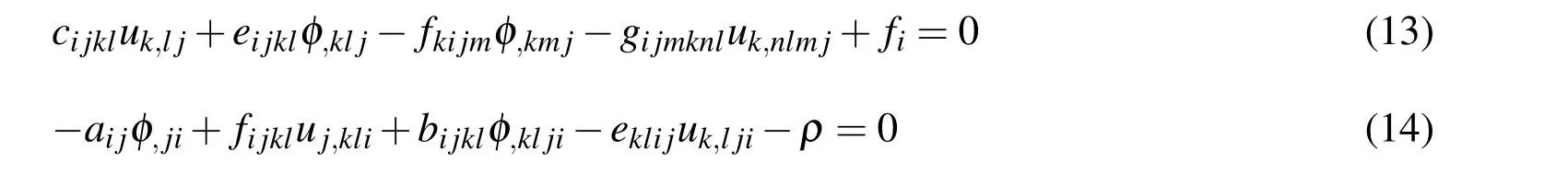
For isotropic dielectric material,the coefficients a,b,c and g are listed as follows:
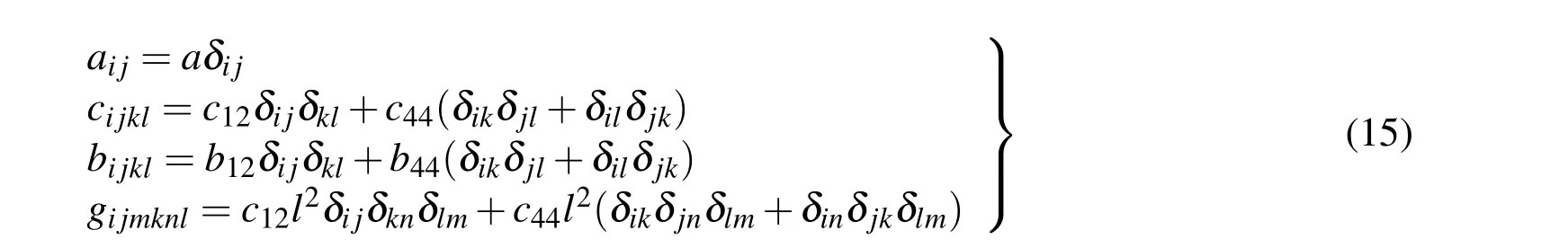
The symmetries of c and g are same with coefficients in Ref.[Gao and Ma(2009)],wherec12,c44are the lame constants andl2having the dimension of length squared is the strain gradient coefficient introduced for isotropic elasticity in Ref.[Gao and Park(2007)].Namely,lis characteristic length of materials which may be related to atomic distance,lattice size,microstructure or others.Refer to[Yang,Zhou and Li(2006)],b has the same symmetry as c as required by symmetry of materials.The non-zero components of a are reduced toa11,a22anda33,which also have the relationa11=a22=a33=adue to isotropy.For flexoelectric tensor f and converse flexoelectric tensor e,Shu et al.(2011)and Quang and He(2011)detailedly investigated the symmetry of the flexoelectric tensors(direct and converse)and the number of independent material parameters for a given symmetry class in different ways.The all non-zero components of e and f for cubic crystals can be listed as below[Shu et al.(2011)]:

Herein,e11,e12,e44andf11,f12,f44are the independent converse flexoelectric and flexoelectric constants respectively.For isotropic materials,the number of independent parameters will reduce from three to two.In other words,there exists a relationship between these non-zero independent components[Shu et al.(2011)]as:f44+2f12=f11,e12+2e44=e11.This will be used in the following derivations.
3 Anti-plane problem
3.1Green’s function solution
For an anti-plane problem,the displacement and electric potential components are represented by:

By substituting Eqs.(15)-(18)into Eq.(13)and Eq.(14),after some simplification and calculation,the final governing equations for anti-plane problems can be expressed as:

By using two-dimensional(2-D)Fourier transforms[Gao and Ma(2012)],the Green’s function for the above two equations can be easily obtained as,respectively:


3.2Solutions of inclusion problem
Consider an infinite homogeneous isotropic dielectric body containing an arbitrary shape Eshelby-type inclusion[Eshelby(1957);Mura(1987)].The body is absence of both body force and body charge but with eigenstrainε ∗(x),eigenstrain gradient w∗(x),eigenelectric field E∗(x),and eigenelectric field gradient V∗(x)prescribed only inside the inclusion.On account of anti-plane problem,the non-vanishing components of eigenfields are as follows:

Following Eshelby’s formalism for inclusion problem,the constitutive equations can be revised to:
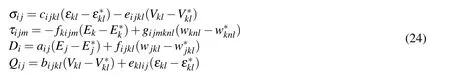
Substituting Eq.(24)into Eqs.(11)-(12)then leads to:

Similarly,by using Eq.(15)-(17)and Eq.(23),Eq.(25)and(26)can be simplified as:

By comparing Eq.(27)and(28)with Eq.(19)and(20),it can be said that,body forceF3is replaced by:
and body electric charge is equivalent to:

According to the definition of Green’s function,the solution of Eq.(27)can be expressed in terms ofG1(x−y)andF3(y)as:
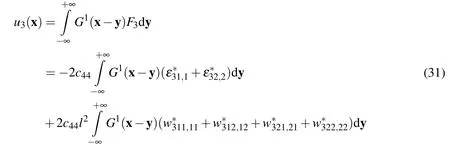

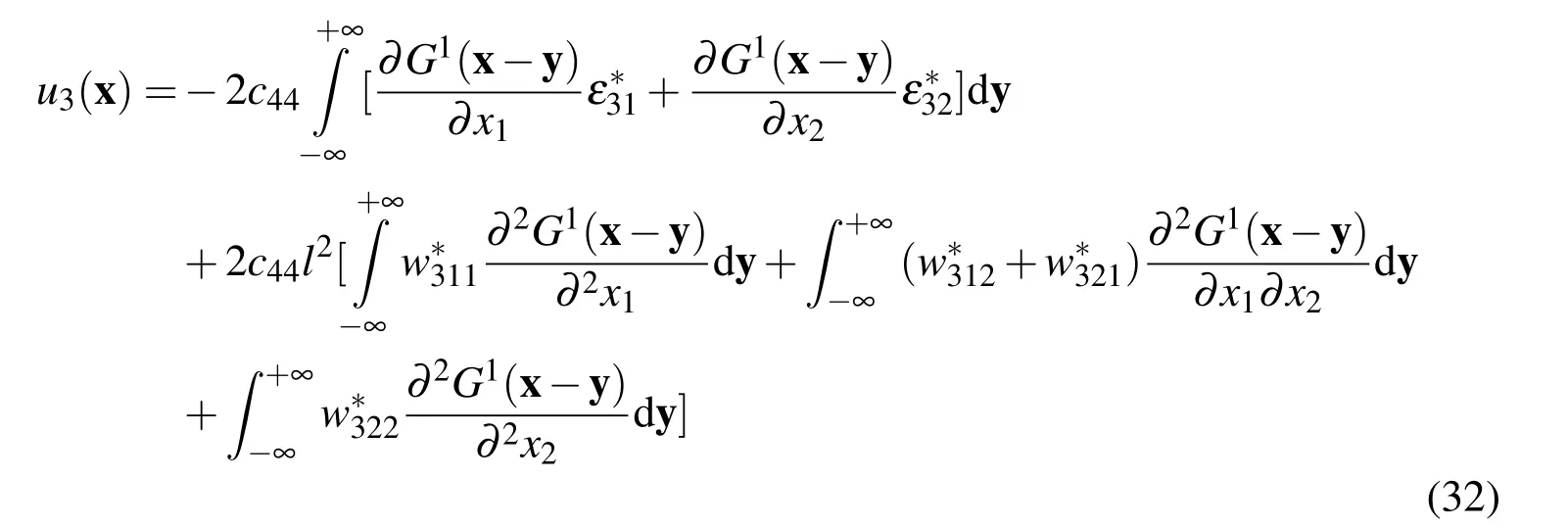
Now the specific case of uniform eigenstrainε∗(x),uniform eigenstrain gradient w∗(x),uniform eigenelectric field E∗(x),and uniform eigenelectric field gradient V∗(x)inside the inclusion occupied by the domain ΩIare considered.Taking into account this fact,Eq.(32)can be further derived to:


Basing on the constraints relation,the strain field can be readily obtained as:

Similarly,the solution of Eq.(28)is given as follows:


From Eq.(35)and Eq.(38),we can explicitly see that strain field and electric filed are uncoupled for this specific anti-plane problem.In other words,strain field is only induced by the prescribed eigenstrain and eigenstrain gradient,while electric filed is just linked to eigenelectric field and eigenelectric field gradient.Based on constitutive laws Eq.(24),the expressions of stress fieldσ(x)and electric displacement D(x)can be obtained simply.Unlike the classical results of antiplane problem where only shear stress and in-plane electric displacement exist,all the components of stress and electric displacement show up in this case.They are listed below as:


Furthermore we notice that the“new”stress components are induced merely by the corresponding electric field gradient components,and the“new”electric displacement components are only caused by the strain gradient.
4 An anti-plane circular inclusion
Figure 1:Schematic of a circular inclusion.
Consider a circular inclusion of radius R with a domain ΩIas show in Fig.1.The analytical expressions of integral of Green’s function are already given in Gao and Ma(2012)as:

For x inside the inclusion,and

For x outside the inclusion,we can obtain analogously

for x inside the inclusion,and


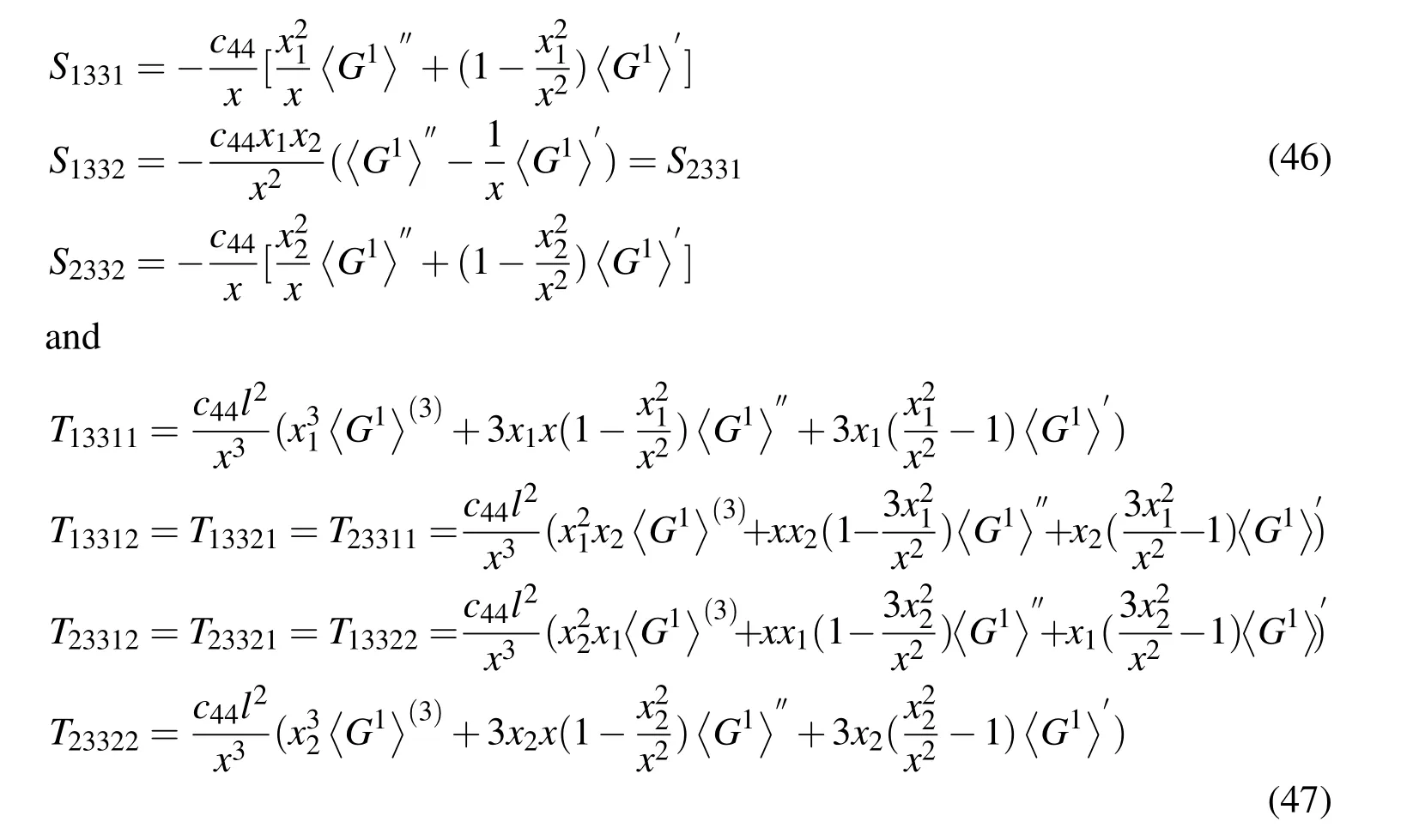
The second order Eshelby tensor and the third order Eshelby-like tensor are shown as:


whereb11=b12+2b44.Using recursion formulas of modified Bessel function(seen in Appendix B),we can readily get:


for x outside the inclusion.By substituting Eq.(50)-(53)into Eq.(46)-(49),the analytical expression of Eshelby and Eshelby-like tensors for elastic and electric field can be easily obtained.When the eigenstrain,eigenstrain gradient,eigenelectric field and eigenelectric field gradient are given,the corresponding strain and electric field can be derived through Eq.(35)and Eq.(38).Furthermore,using Eq.(40)and Eq.(41)leads to the stress and electric displacement quantities which represent high-order electromechanical coupling to some extent.
5 Numerical results
To numerically illustrate the results obtained above,we now choose NaCl material,which is a centrosymmetric dielectrics,to give a series of numerical results.The flexoelectric constants of NaCl are estimated by means of empirical lattice dynamics[Maranganti and Sharma(2009)].In nano-inclusion problems,as a typical microstructure,the influences of inclusion size are what we most interested in.Therefore,we choose the characteristic length asl=m=2nm by reference to inclusion size.Fig.2 shows Eshelby tensor incorporating gradient effects for elastic field.
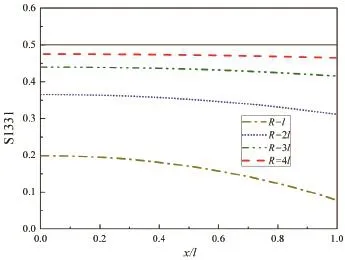
Figure 2:Eshelby tensor of strain along a radial direction of the inclusion.
From Figure 2,it is seen thatS1331varies with the position x and the inclusion sizeR,unlike the classical results which is a constant inside the inclusion(the straight line).The differences between the lines to the classical one are due to the strain gradient effects.WhileRis small,the strain gradient effects are very large and should not be ignored.
However,the values approach gradually to the result of classical elasticity with increase of inclusion radius.It is noted that on account of the decoupling results of anti-plane inclusion problem of dielectrics,our results of elastic Eshelby tensor are in accordance with solutions derived by Gao and Ma(2012)who used the simplified strain gradient elasticity theory(SSGET)sloving Eshelby-type anti-plane strain inclusion problem.Likewise,Fig.3 gives Eshelby tensor with electric field gradient effects for electric field.We can clearly figure out thatM11are no longer uniform,and have similar tendency withS1331for different position and inclusion size.

Figure 3:Eshelby tensor of electric field along a radial direction of the inclusion.


Figure 4:The strain field as a function of position and inclusion size.

Figure 5:The electric field as a function of inclusion size for fixed positions.

Figure 6:High-order electromechanical coupling coefficient versus piezoelectric coefficient.

In the present paper we intensively focus on the analytical results.Pure analytical derivations may work for infinite domain inclusion problem while real micro-structures are more complexed.Combining of analytical and numerical methods[Dong and Atluri(2012a);Dong and Atluri(2012b);Bishay,Dong and Atluri(2014)]is a powerful tool for direct numerical simulations of realistic problems of real material structures,which provide valuable insights for our future work.
6 Conclusions
In summary,we analyze the elastic and electric field of anti-plane inclusion problem by incorporating both strain and electric field gradient effect for centrosymmetric dielectrics.The Eshelby tensor,Eshelby-like tensor,strain field,electric field,stress and electric displacement are analytically derived by means of Green’s function method.Unlike the classical results,all the physical quantities taken in account to gradient effects show strongly size-dependent features.Our results indicate that strain and electric field are decoupled which is reasonable.And more importantly,the high order electroelastic coupling appears between stress and electric field.The components of stress which do not exist in classical case can be induced by the electric gradient,and the out-plane electric displacement component can be caused by the strain gradient,that is an good interpretation of flexoelectric coupling effects.The numerical results reveal that,firstly,the strain and electric field gradient effects are significantly strong and should not be ignored when the inclusion size is small.Secondly,the results gradually approach to the classical solution as increase of the inclusion radius.Thirdly,the high-order electromechanical coupling effect in centrosymmetric dielectrics(non-piezoelectric materials)can be equivalent to piezoelectric effect in traditional piezoelectric materials when the inclusion size is small.
Acknowledgement:The supports from NSFC(Grants No. 11025209,11372238,11302161,11321062 and 11302162)are appreciated.
Bishay,P.L.;Dong,L.;Atluri,S.N.(2014).Multi-physics computational grains(MPCGs)for direct numerical simulation(DNS)of piezoelectric composite/porous materials and structures.Computational Mechanics,DOI:10.1007/s00466-014-1044-y
Cheng,Z.;He,L.(1995):Micropolar elastic fields due to a spherical inclusion.International Journal of Engineering Science,vol.33,no.3,pp.389-397.
Cross,L.E.(2006):Flexoelectric effects:Charge separation in insulating solids subjected to elastic strain gradients.Journal of materials science,vol.41,no.1,pp.53-63.
Dong,L.;Atluri,S.N.(2012a):Development of 3D Trefftz Voronoi Cells with Ellipsoidal Voids&/or Elastic/Rigid Inclusions for Micromechanical Modeling of Heterogeneous Materials.Computers Materials and Continua,vol.30,no.1,pp.39-81.
Dong,L.;Atluri,S.N.(2012b):Development of 3D T-Trefftz Voronoi cell finite elements with/without spherical voids&/or elastic/rigid inclusions for micromechanical modeling of heterogeneous materials.Computers Materials and Continua,vol.29,no.2,pp.169
Eshelby,J.D.(1957):The determination of the elastic field of an ellipsoidal inclusion,and related problems.Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences,vol.241,no.1226,pp.376-396.
Gao,X.;Ma,H.(2009):Green’s function and Eshelby’s tensor based on a simplified strain gradient elasticity theory.Acta Mechanica,vol.207,pp.163-181.
Gao,X.;Ma,H.(2010):Strain gradient solution for Eshelby’s ellipsoidal inclusion problem.Proceedings of the Royal Society A:Mathematical,Physical and Engineering Sciences,vol.466,no.2120,pp.2425-2426.
Gao,X.;Ma,H.(2012):Strain gradient solution for the Eshelby-type anti-plane strain inclusion problem.Acta Mechanica,vol.223,no.5,pp.1067-1080.
Gao,X.;Park,S.(2007):Variational formulation of a simplified strain gradient elasticity theory and its application to a pressurized thick-walled cylinder problem.International Journal of Solids and Structures,vol.44,pp.7486-7499.
Hu,S.;Shen,S.(2009):Electric Field Gradient Theory with Surface Effect for Nano-Dielectrics.CMC-Computers,Materials&Continua,vol.13,no.1,pp.63-88.
Liang,X.;Shen,S.(2013):Size-dependent piezoelectricity and elasticity due to the electric field-strain sradientcoupling and strain gradientelasticity.International Journal of Applied Mechanics,vol.5,no.2,pp.1350015.
Liu,C.;Hu,S.;Shen,S.(2012):Effect of flexoelectricity on electrostatic potential in a bent piezoelectric nanowire.Smart Materials and Structures,vol.21,no.11,pp.115024.
Liu,C.;Hu,S.;Shen,S.(2014):Effect of Flexoelectricity on Band Structures of One-Dimensional Phononic Crystals.ASME Journal of Applied Mechanics,vol.81,no.5,051007.
Lubarda,V.A.(2003):Circular inclusions in anti-plane strain couple stress elasticity.International Journal of Solids and Structures,vol.40,no.15,pp.3827-3851.
Ma,H.M.;Gao,X.L.(2010):Eshelby’s tensors for plane strain and cylindrical inclusions based on a simplified strain gradient elasticity theory.Acta Mechanica,vol.211,pp.115-129.
Ma,W.(2008):A study of flexoelectric coupling associated internal electric field and stress in thin film ferroelectrics.physica status solidi(b),vol.245,no.4,pp.761-768.
Maranganti,R.;Sharma,N.;Sharma,P.(2006):Electromechanical coupling in nonpiezoelectric materials due to nanoscale nonlocal size effects:Green’s function solutions and embedded inclusions.Physical Review B,vol.74,no.1,014110.
Maranganti,R.;Sharma,P.;(2009):Atomistic determination of flexoelectric properties of crystalline dielectrics.Physical Review B,vol.80,no.5,054109.
Mindlin,R.D.(1968):Polarization gradient in elastic dielectrics.International Journal of Solids and Structures,vol.4,no.6,pp.637-642.
Mura,T.(1987)Micro-mechanics of Defects in Solids,vol 3.Springer.
Quang,H.;He,Q.(2011):The number and types of all possible rotational symmetries for flexoelectric tensors.Proceedings of the Royal Society A:Mathematical,Physical and Engineering Science,vol.467,no.2132,pp.2369-2386.
Sharma,N.;Maranganti,R.;Sharma,P.(2007):On the possibility of piezoelectric nanocomposites without using piezoelectric materials.Journal of the Mechanics and Physics of Solids,vol.55,pp.2328-2350.
Sharma,N.D.;Landis,C.M.;Sharma,P.(2010):Piezoelectric thin-film superlattices without using piezoelectric materials.Journal of Applied Physics,vol.108,no.2,024304.
Sharma,P.;Ganti,S.(2004):Size-dependent eshelby’s tensor for embedded nano-inclusions incorporating surface/interface energies.ASME Journal of Applied Mechanics,vol.71,no.5,pp.663-671.
Shen,S.;Hu,S.(2010):A theory of flexoelectricity with surface effect for elastic dielectrics.Journal of the Mechanics and Physics of Solids,vol.58,no.5,pp.665-677.
Shu,L.;Wei,X.;Pang,T.;Yao,X.;Wang,C.(2011):Symmetry of flexoelectric coefficients in crystalline medium.Journal of Applied Physics,vol.110,no.10,104106.
Wang,X.;Pan,E.;Feng,W.(2008):Anti-plane Green’s functions and cracks for piezoelectric material with couple stress and electric field gradient effects.European Journal of Mechanics-A/Solids,vol.27,no.3,pp.478-486.
Xu,Y.;Hu,S.;Shen,S.(2013):Electrostatic potential in a bent flexoelectric semiconductive nanowire.CMES:Computer Modeling in Engineering&Sciences,vol.91,no.5,pp.397-408.
Yan,Z.;Jiang,L.(2013):Flexoelectric effect on the electroelastic responses of bending piezoelectric nanobeams.Journal of Applied Physics,vol.113,no.19,194102.
Yang,J.;Zhou,H.;Li,J.(2006):Electric field gradient effects in an anti-plane circular inclusion in polarized ceramics.Proceedings of the Royal Society A:Mathematical,Physical and Engineering Science,vol.462,pp.3511-3522.
Yang,S.;Hu,S.;Shen,S.(2012):Local electroelastic field and effective electroelastic moduli of piezoelectric nanocomposites with interface effect.CMCComputers,Materials and Continua,vol.29,no.3,pp.279-298.
Zhang,X.;Sharma,P.(2005):Size dependency of strain in arbitrary shaped anisotropic embedded quantum dots due to nonlocal dispersive effects.Physical Review B,vol.72,195345.
Zubko,P.;Catalan,G.;Tagantsev,A.K.(2013):Flexoelectric effect in solids.Annual Review of Materials Research,vol.43,pp.387-421.
Appendix A
For a sufficiently smooth functionF(x),the following differential relations hold:

Appendix B
Recursion formulas of modified Bessel function are expressed as:
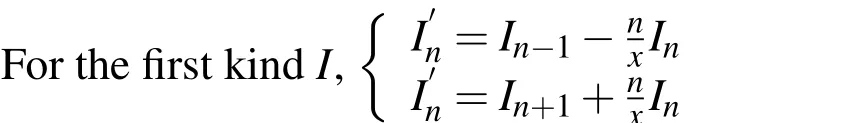

杂志排行
Computers Materials&Continua的其它文章
- Optimization of Johnson-Cook Constitutive Model for Lead-free Solder Using Genetic Algorithm and Finite Element Simulations
- Effect of Gravitational Field and Temperature Dependent Properties on Two-Temperature Thermoelastic Medium with Voids under G-N Theory
- Numerical Study on Mechanical Properties of Steel Fiber Reinforced Concrete by Statistical Second-order Two-scale Method
